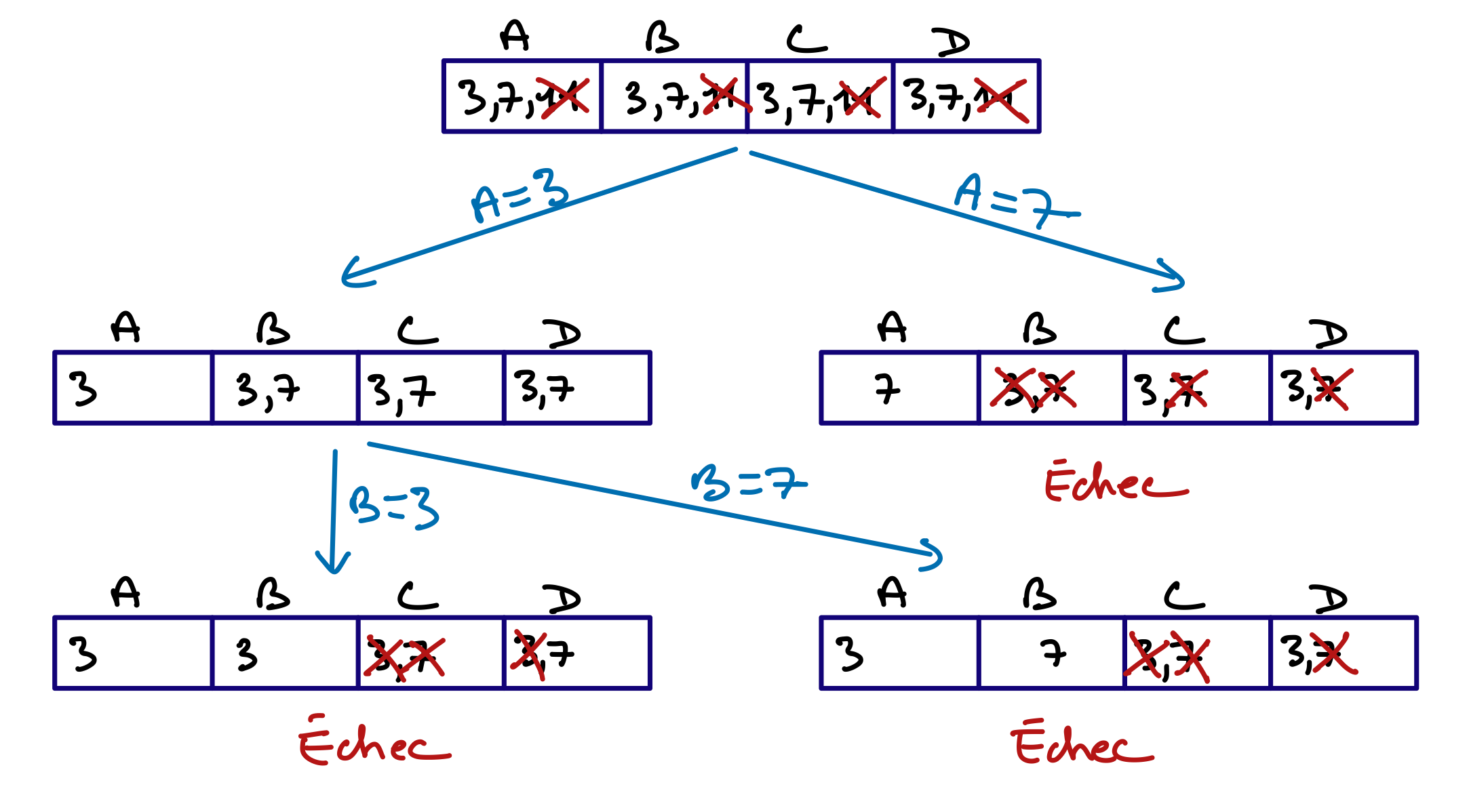
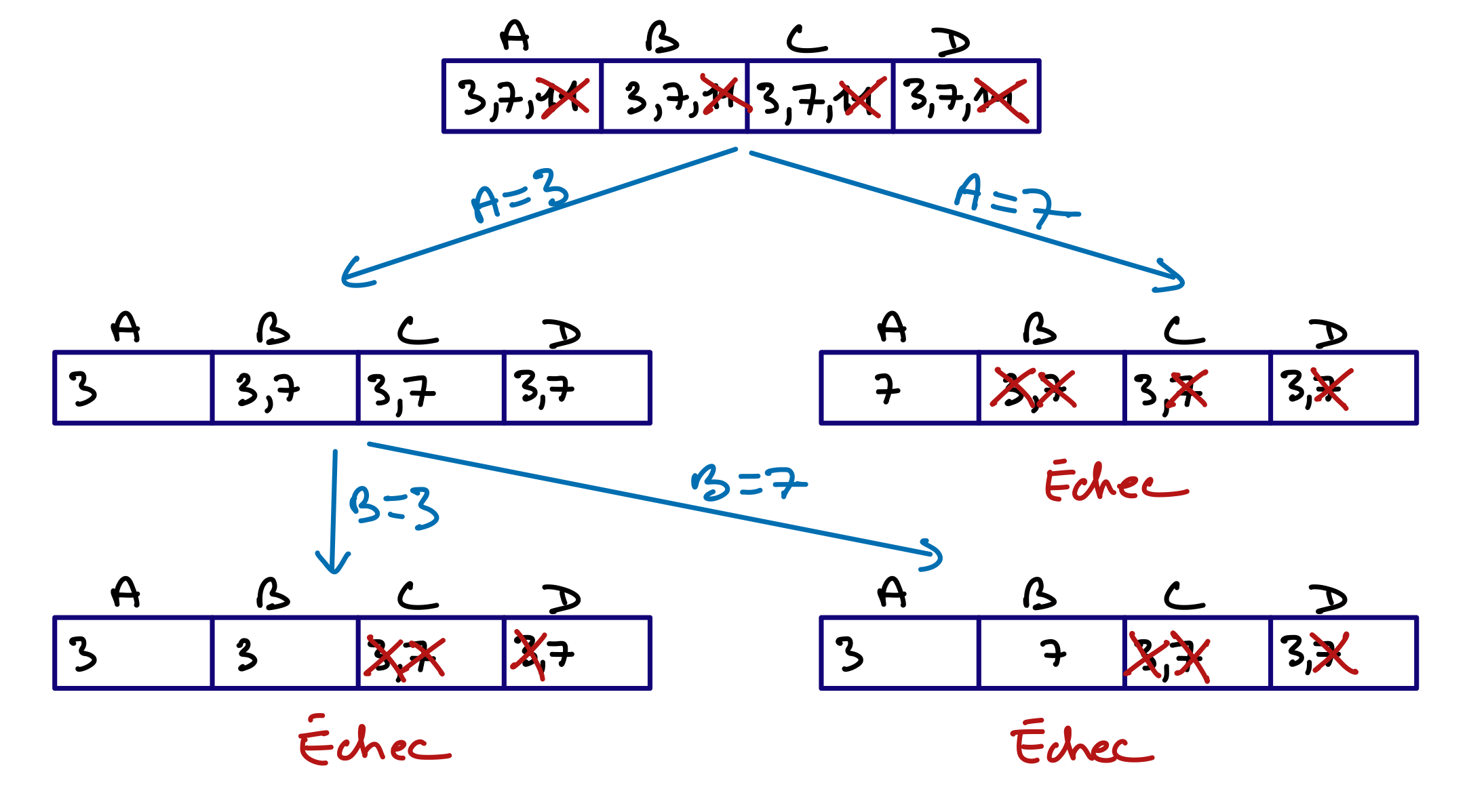
Test partie B

Classes et objets

Introduction

On souhaite réaliser une classe permettant de gérer des tableaux extensibles de valeurs Booléennes. Par tableau extensible, on entend qu’il est possible de lire ou d’écrire une valeur au-delà de la taille d’un tableau, ce que ne permettent pas les tableaux classiques.

Prenons un exemple. Je crée (dans une méthode) un tableau classique de boolean de longueur 5 comme ceci.

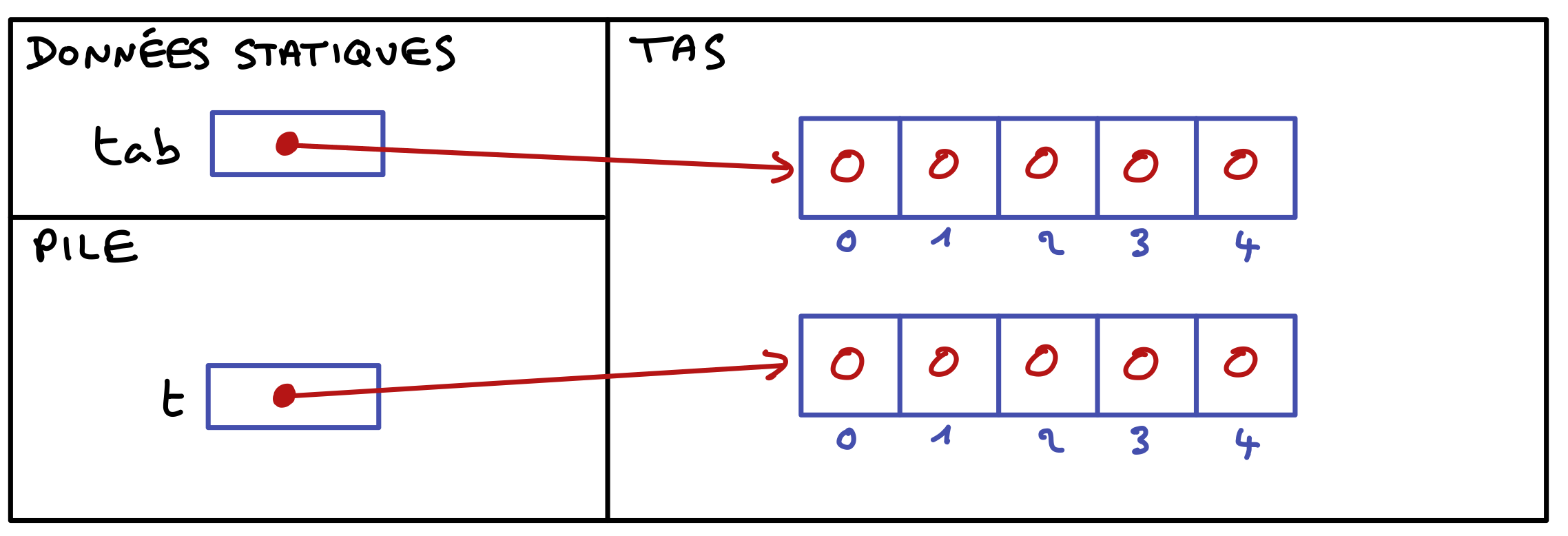
boolean[] tb = new boolean[5];

J’obtiens un tableau de 5 cellules, numérotées de 0 à 4, qui contiennent toutes la valeur false (c’est la valeur par défaut des cellules lorsqu’on crée un tableau de valeurs de type boolean).

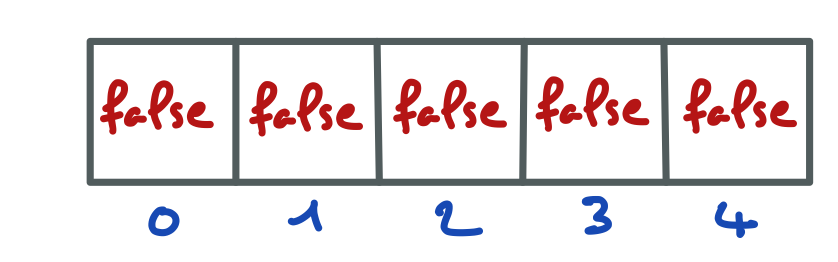
Je peux facilement changer la valeur d’une cellule d’indice entre 0 et 4, mais si je tente d’écrire une valeur dans la cellule d’indice 7…

tb[7] = true;

… le programme s’arrête avec pertes et fracas en affichant un message d’erreur. Même problème si je tente de lire la valeur tb[10], par exemple.

Avec un tableau extensible, ces opérations sont autorisées. Imaginons que nous disposions d’une classe BoolExt représentant un tableau extensible de boolean. Pour créer un tel tableau, j’écris…

BoolExt te = new BoolExt();

… ce qui crée un tableau extensible de taille 1. Ce tableau n’a qu’une seule cellule et elle a la valeur false. Je ne peux pas l’utiliser avec les crochets car il ne s’agit pas d’un vrai tableau mais d’une instance de la classe BoolExt. Pour écrire ou lire des valeurs dans ce tableau extensible, je dois utiliser des méthodes spécifiques.

Je peux écrire une valeur à la position de mon choix, même au-delà de la taille actuelle du tableau, avec la méthode write. Par exemple…

te.write(4, true);

…a pour effet d’agrandir le tableau et de placer la valeur true en position 4. L’objet désigné par la variable te représente alors le tableau suivant.

Au lieu de produire une erreur, l’écriture dans la cellule d’indice 4 a provoqué l’agrandissement du tableau et les nouvelles cellules crées entre les indices 0 et 4 ont été remplie avec la valeur false.

Pour lire la valeur contenue dans une cellule, je dois utiliser la méthode read. Par exemple…

System.out.println(te.read(2));
System.out.println(te.read(4));

… produit l’affichage false true.

Mais il y a mieux encore. J’ai le droit de lire le contenu d’une cellule située au-delà de la fin du tableau. Au lieu de produire une erreur comme avec les tableaux ordinaires, cette opération retourne false, comme si le tableau avait une longueur illimitée et que toutes les valeurs situées après le dernier true étaient false. Ainsi, par exemple, la ligne…

System.out.println(te.read(7));

… produit l’affichage false.

Le fait d’écrire false à un emplacement situé après le dernier true, comme par exemple…

te.write(11, false);

…est équivalent à ne rien faire du tout puisque la position 11 est située au-delà de la position du dernier true (qui est à l’indice 4) et que toute lecture à cette position retournera false.

Récapitulons.

Tout se passe comme si un tableau extensible comportait une partie concrète, effectivement représentée en mémoire par un tableau de boolean, prolongé par une partie imaginaire infinie, non représentée en mémoire, dont toutes les cellules sont supposées contenir la valeur false.

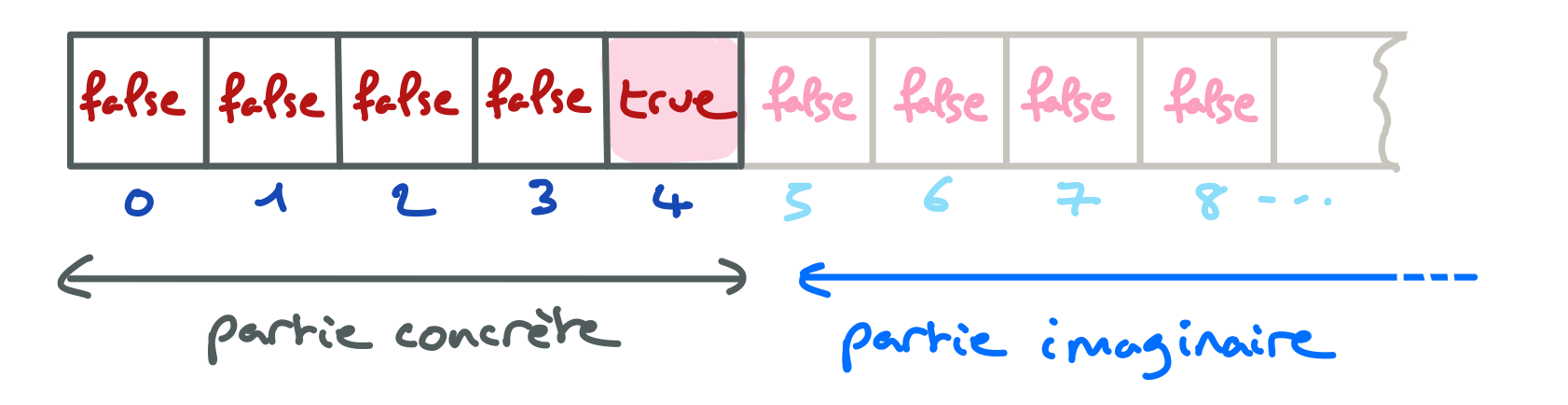
On appelle taille du tableau le nombre de cellules de la partie concrète. Cette parie concrète sera effectivement représentée en mémoire par un tableau de boolean désigné par un attribut de la classe BoolExt. La partie imaginaire est le prolongement imaginaire infini de la partie concrète et toutes les cellules de cette partie imaginaire sont supposées contenir la valeur false.

Attention ! Il n’y a pas nécessairement la valeur true dans la dernière cellule de la partie concrète car pour ne pas compliquer le code, l’écriture d’une valeur false à la place du dernier true ne provoque pas le rétrécissement de la partie concrète.

Par exemple, à l’issue de l’exécution du code suivant…

BoolExt te = new BoolExt();
te.write(4, true);
te.write(3, true);
te.write(4, false);

… la partie concrète du tableau est la suivante.

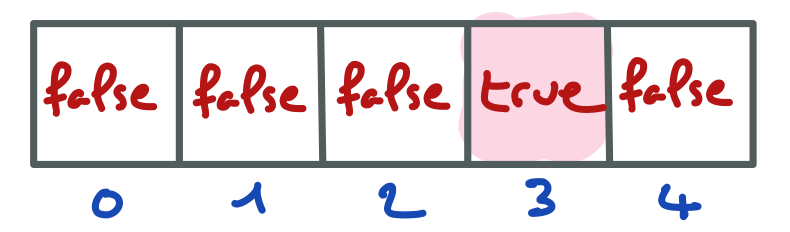
Elle a une longueur égale à 5 parce qu’à un moment donné, la valeur true la plus éloignée du début était en position 4, bien qu’elle ait ensuite été remplacée par false.

Q1

Vous devez compléter la classe BoolExt en donnant les codes du constructeur et des méthodes adjust, et read. Pour comprendre le rôle de la méthode ajust, analysez le code de la méthode write.

public class BoolExt
{
   private boolean[] data;
 
   public BoolExt() 
   {
     // À compléter  
   }
 
   private void adjust(int newSize) 
   {
     // À compléter  
   }
 
   public void write(int index, boolean value) 
   {
      if((index >= data.length) && (value == true))
      {
        adjust(index+1);
      }
      data[index] = value;
   }
 
   public boolean read(int index) 
   {
     // À compléter 
   }
 
   public int size() 
   {
     return data.length;
   }
 
   public String toString()
   {
     String r = "";
     for(int i=0; i < data.length; i++)
     {
       if(data[i]) r = r + "1";
       else r = r + "0";
     }
     return r;
   }
}

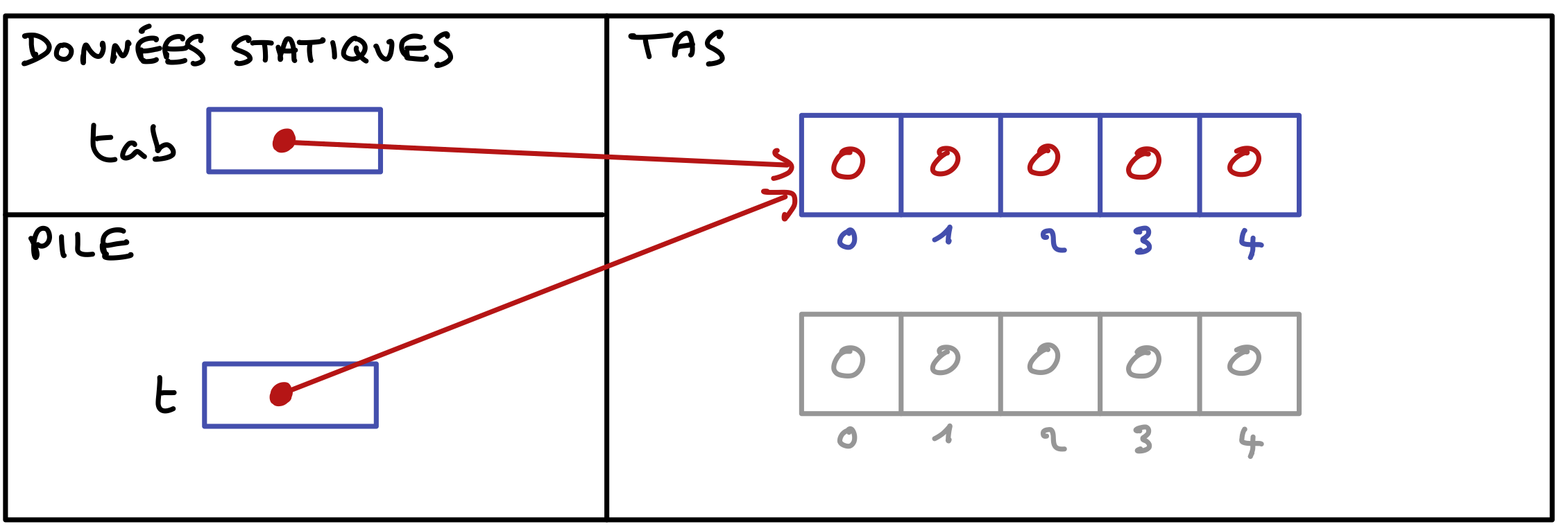
La méthode ajust augmente la taille de la partie concrète, c’est-à-dire la taille du tableau désigné par l’attribut data, de manière à ce que la nouvelle taille soit égale à la valeur du paramètre newSize. En pratique, java ne permet pas de redimensionner un tableau, donc cette opération suppose de créer un nouveau tableau plus grand dans lequel le contenu de l’ancien tableau est recopié, puis de remplacer l’ancien tableau par le nouveau.

Cette méthode adjust est appelée par la méthode write lors d’une écriture d’une valeur true dans une cellule située au-delà de la limite de la partie concrète. (Dans le cas de l’écriture d’une valeur false, un agrandissement n’est pas nécessaire puisque toutes les valeurs situées dans la partie imaginaire sont considérées comme false).

Notez que la méthode toString utilise les caractères 0 et 1 à la place de false et true pour des raisons de lisibilité et concision.

Commencez par le constructeur, qui doit créer un tableau extensible de une cellule contenant false.

Merci de transmettre votre réponse au responsable de l’unité d’enseignement via Teams.

Ensuite, donnez le code de la méthode adjust qui augmente la taille du tableau désigné par l’attribut data. En pratique, on ne peut par rallonger un tableau donc la seule solution est de le remplacer par un tableau plus grand. Mais il faut recopier le contenu de l’ancien tableau dans le nouveau.

Merci de transmettre votre réponse au responsable de l’unité d’enseignement via Teams.

Maintenant, donnez le code de la méthode read, en prenant en compte le fait que l’indice de la cellule à lire peut se situer au delà de la partie concrète du tableau, et que dans ce cas la valeur à retourner est false.

Merci de transmettre votre réponse au responsable de l’unité d’enseignement via Teams.

Q2

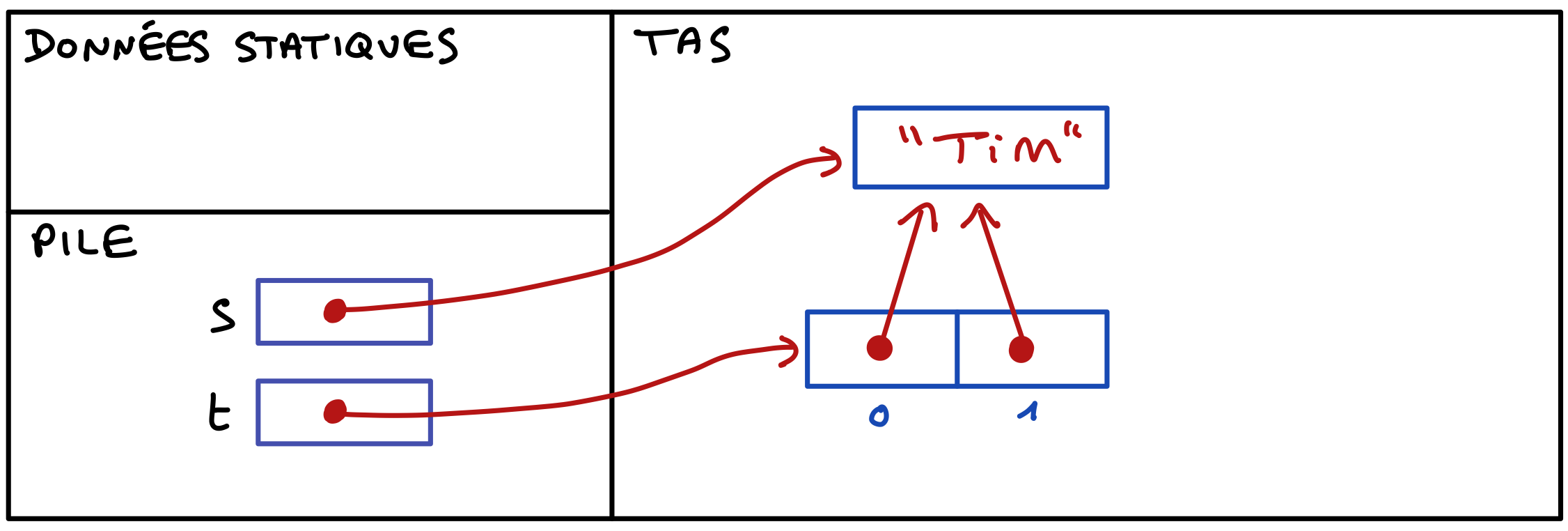
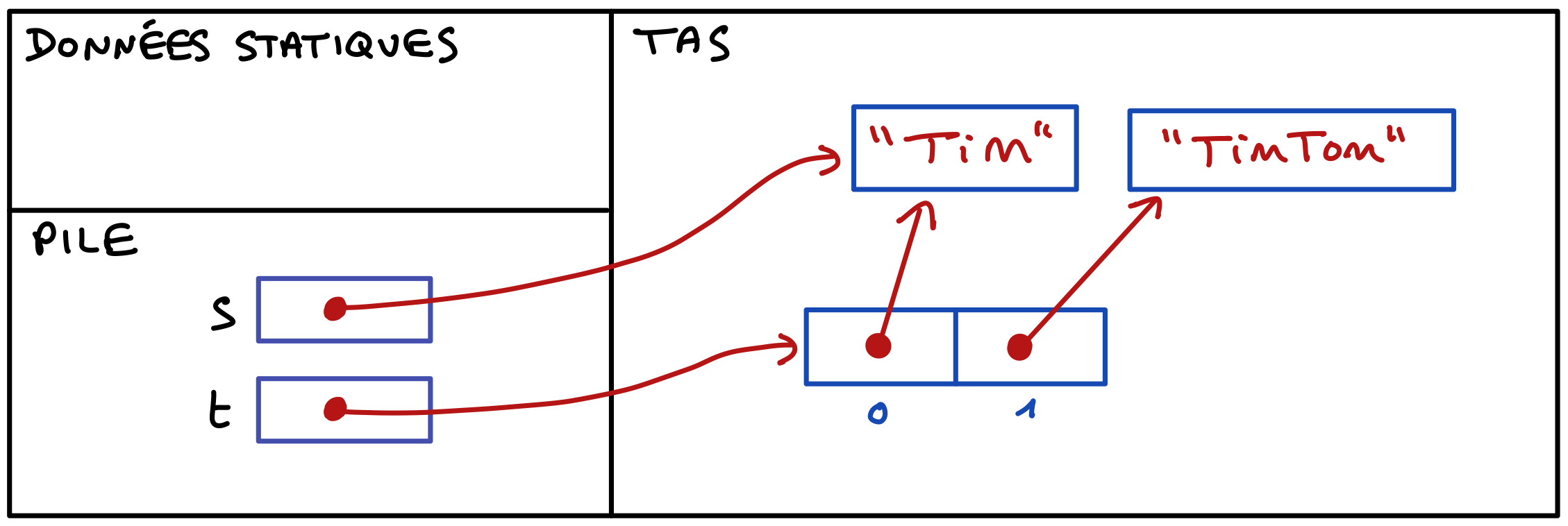
Réalisez un constructeur en copie pour la classe BoolExt. Ce constructeur doit accepter en paramètre une instance de BoolExt et créer une nouvelle instance identique mais complètement indépendante en mémoire.

Merci de transmettre votre réponse au responsable de l’unité d’enseignement via Teams.

Q3

Dessinez la représentation en mémoire, dans la pile et le tas, des données créées par les lignes de code suivantes.

BoolExt t1 = new BoolExt() ;
t1.write(5, true);
t1.write(1, true);
BoolExt t2 = t1;
BoolExt t3 = new BoolExt(t1);

Merci de transmettre votre réponse au responsable de l’unité d’enseignement via Teams.

Partie A

Programmation procédurale en Java

Q1

public class Main
{
    public static void test()
    {
       System.out.println("Bonjour");
    }
    public static void main(String[] args)
    {
       System.out.println(test());
    }
}

Ce programme compile-t-il ? Si oui qu’est ce qui est affiché à son exécution ? Si non pourquoi ?

public static void main(String[] args)
{
   test();
}

Q2

public class Main
{
    public static String test()
    {
       return System.out.println("Bonjour");
    }
    public static void main(String[] args)
    {
       System.out.println(test());
    }
}

Ce programme compile-t-il ? Si oui qu’est ce qui est affiché à son exécution ? Si non pourquoi ?

public static String test()
{
   return "Bonjour";
}

Q3

Soit la méthode suivante :

    public static int m1(int k)
    {
        int sum = 0;
        for(int i=1; i<=k; i=i+2)
        {
            sum = sum + i;
        }
        return sum;
    }

Quelle est la valeur retournée par m1(3) et par m1(5) ?

Q4

Soit la classe suivante.

public class Main
{
    public static int[] tab = new int[5];

    public static void printTabInt(int[] t)
    {
        for(int i=0; i<t.length; i++)
        {
            System.out.print(t[i] + " ");
        }
        System.out.println();
    }

    public static void test1()
    {
        int[] t = new int[5];
        t = tab; t[2] = 12;
        printTabInt(tab);
    }

    public static void test2()
    {
        int[] t = tab;
        t[2] = 12;
        printTabInt(tab);
    }

    public static void main(String[] args)
    {
        test1(); test2();
    }
}

Ce programme compile-t-il ou comporte-t-il une erreur ?

Les deux appels à test1 et test2 produisent-ils exactement le même affichage à l’écran ?

    public static void test1()
    {
        int[] t = new int[5];   // ligne A
        t = tab;                // ligne B
        t[2] = 12;
        printTabInt(tab);
    }

Q5

Soit la classe suivante.

public class Main
{
    public static int[] tab = new int[5];

    public static void printTabInt(int[] t)
    {
        for(int i=0; i< t.length; i++)
        {
            System.out.print(t[i] + " ");
        }
        System.out.println();
    }

    public static void test1()
    {
        int[] t = new int[5];
        t[3] = 5;
        t = tab; 
        t[2] = 12;
        printTabInt(t);
        printTabInt(tab);
    }

    public static void main(String[] args)
    {
        test1();
    }
}

Donnez les affichages réalisés par l’exécution du programme.

0 0 12 0 0 
0 0 12 0 0 

Q6

Soit les lignes de code suivantes :

String[] t = new String[2];
String s = "Tim";
t[0] = s; t[1] = s;

Dessinez les données en mémoire à l’issue de l’exécution de ces lignes.

Q7

Soit les lignes de code suivantes :

String[] t = new String[2];
String s = "Tim";
t[0] = s; 
t[1] = t[0] + "Tom";

Dessinez les données en mémoire à l’issue de l’exécution de ces lignes.

Vous avez commis des erreurs ? N’ayez aucune inquiétude. Le but de ce test était de vous faire commettre quelques erreurs pour attirer votre attention sur certaines subtilités. Vous devez vous expliquer à vous-même (vous auto-expliquer) ces erreurs et comment il fallait raisonner pour les éviter.

Au besoin, reprenez les ressources pédagogiques de la partie A pour revoir les points problématiques. N’hésitez pas à poser des questions à votre enseignant. Après avoir bien compris vos erreurs, retaites le test, mais pas tout de suite ! Attendez au moins une semaine, voire deux.