Archives de catégorie : Test

C et C++ partie E

Par O. Bailleux, Maître de conférences HDR à l'université de Bourgogne.

Tableaux dynamiques

Les activités #.dec (dec pour Découverte) consistent à étudier des présentations explicatives et à traiter tous les exercices de découverte proposés. Si vous ne répondez pas correctement à un exercice de découverte, revenez en arrière pour relire les explications et identifier la cause de votre erreur.

Les activités #.ent (ent pour Entrainement) consistent à traiter des exercices d’entraînement. Vous devez d’abord tenter de traiter ces exercices sans dévoiler d’indice ni regarder la solution. Vous pouvez remonter dans le document pour relire certaines explications ou consulter les solutions des exercices de découverte ou d’entraînement précédemment traités.

Activité de découverte E.dec

E.dec1 : Tableau dynamique

Prérequis

Maîtriser la partie C (tableaux et pointeurs) et la partie D (chaînes de caractères)

Objectif

Créer un tableau pouvant être détruit lorsqu’on en a plus besoin.

Dans la partie C, nous avons vu deux sortes de tableaux :

Les tableaux globaux, qui sont créés en début de l’exécution du programme et existent pendant toute la durée de son exécution. Ils peuvent être très grands (taille limitée par la mémoire disponible) et sont accessibles par toutes les fonctions du programme.
Les tableaux locaux qui n’existent que pendant l’exécution de la fonction dans laquelle ils sont déclarés et ne sont accessibles que dans cette fonction où dans une autre fonction qui à accès à leur adresse mémoire. La taille d’un tableau local est limitée par celle de la pile d’exécution.

Mais il arrive qu’on souhaite utiliser un tableau de taille arbitrairement grande (dans la limite de la mémoire disponible) pendant une durée qui n’est ni celle de l’exécution du programme, ni celle de l’exécution d’une fonction particulière. Typiquement, un tableau créé dans une fonction et détruit dans une autre.

Moyen

Réservation d’un bloc mémoire dans le tas

Il existe une zone mémoire que nous n’avons encore jamais utilisée et qui est appelée le tas (Heap en anglais). Il est possible de réserver dans cette zone des blocs mémoire pouvant notamment être utilisés comme des tableaux. Voici un exemple de fonction qui crée dans le tas une chaîne de caractère contenant la concaténation de deux chaînes passées en arguments.

char* concat(const char* s1, const char* s2)
{
    int n1 = strlen(s1);                     
    int n2 = strlen(s2);
    char* out = (char*) malloc((n1+n2+1)*sizeof(char));  // A
    strcpy(out, s1);                                     // B
    strcpy(out + n1, s2);                                // C
    return out;                                          // D
}

La fonction main suivante donne un exemple d’utilisation.

int main()
{
    char t[] = "Tim ";
    char u[] = "et Tom";
    char* s = concat(t, u);
    printf("%s\n", s);
    return 0;
}

Il y a beaucoup de choses à dire à propos de cet exemple. La première est que, contrairement à la fonction standard strcat, la fonction concat crée une nouvelle chaîne, indépendante des deux chaînes désignées par les paramètres s1 et s2, et qui est stockée dans une nouvelle zone mémoire située dans le tas.

Le bloc mémoire contenant la chaîne retournée par concat est réservé dans le tas par un appel, en ligne A, à la fonction standard malloc, dont le nom est une abréviation de "memory allocation".

void* malloc( size_t size );

Cette fonction réserve un bloc mémoire de la taille indiquée en paramètre et en retourne l’adresse. Si la réservation est impossible, la valeur de retour est NULL. Cela se produit seulement quand il ne reste plus de zone mémoire de la taille demandée, soit parce que toute la mémoire à été utilisée, soit parce qu’elle est fragmentée.

La valeur de retour de malloc est de type void*, qu’on pourrait traduire par "pointeur sur n’importe quoi". En effet, malloc peut être utilisée pour réserver des blocs permettant de stocker n’importe quel type de données. Un cast, aussi appelé transtypage, est nécessaire pour placer l’adresse du bloc dans la variable out qui est de type pointeur sur char. Dès lors, ce bloc pourra être utilisé comme un tableau de caractères, et donc contenir une chaîne.

Exercice de découverte E.dec.x1

Pourquoi la taille du bloc est-elle égale à 1 plus la somme des tailles des chaînes désignées par les paramètres ?

"Réponse"

Le bloc doit recevoir la concaténation des chaînes désignées en paramètres. Il faut que sa taille permette le stockage des caractères de ces deux chaînes plus le marqueur de fin de chaîne.

L’exécution de la ligne A place donc dans la variable out l’adresse d’un bloc mémoire de n1 + n2 + 1 octets situé dans le tas.

    char* out = (char*) malloc((n1+ n2+1)*sizeof(char)); // A

Le bloc retourné par malloc n’est pas initialisé. Son contenu est imprévisible.

En vertu de la correspondance entre tableaux et pointeurs, l’adresse du bloc peut être utilisée comme un nom de tableau et le bloc peut être utilisé comme un tableau.

Exercice de découverte E.dec.x2

Donnez les lignes de code à ajouter juste après la ligne A pour initialiser à 0xFF tous les octets du bloc venant d’être réservé.

"Réponse"

    for(int i=0; i< n1+n2+1; i++)
    {
        out[i] = 0xFF;
    }

Le tableau dynamique s’utilise strictement de le même manière que les tableaux que nous avons vu jusqu’ici.

Le reste de la définition de la fonction concat fait appel aux connaissances abordées précédemment. On copie bout à bout les chaînes à concaténer dans le nouveau bloc mémoire, dont l’adresse est ensuite retournée.

Exercice de découverte E.dec.x3

La compilation de la fonction suivante, censée avoir le même rôle que la version précédente, produit un avertissement.

char* concat(const char* s1, const char* s2)
{
    int n1 = strlen(s1);                     
    int n2 = strlen(s2);
    char out[n1 + n2 + 1];
    strcpy(out, s1);            
    strcpy(out + n1, s2);       
    return out;         
}

Qu’est-ce qui ne va pas avec cette fonction ?

"Réponse"

Le tableau out est une variable locale. Contrairement à un tableau dynamique réservé dans le tas, ce tableau local est détruit à l’issue de l’exécution de la fonction. Son utilisation ultérieure peut avoir des conséquences imprévisibles et entraîner de graves problèmes tels que plantage, écrasement des valeurs de certaines variables…

Exercice de découverte E.dec.x4

La création de la chaîne retournée par la fonction concat est réalisée par ces deux lignes :

    strcpy(out, s1);            
    strcpy(out + n1, s2);

On aurait pu la réaliser comme ceci :

    strcpy(out, s1);            
    strcat(out, s2);

Quel est l’intérêt de la première solution par rapport à la deuxième ?

"Réponse"

La fonction strcat doit d’abord localiser le marqueur de fin de la chaîne de destination avant de commencer à recopier à la suite la chaîne désignée par s2. La première version est plus efficace, bien que la différence ne soit pas visible en pratique.

Bonus

Réserver un bloc initialisé à 0 avec calloc

Nous avons vu que la fonction malloc n’initialise pas le bloc qu’elle réserve dans le tas. Il existe une autre fonction permettant de réserver un bloc et de le remplir avec des valeurs 0.

void* calloc( size_t elementCount, size_t elementSize );

La taille du bloc réservé est égale à elementCount * elementSize. Ce bloc est initialisé avec des octets 0x00. Par exemple, la ligne suivante…

int* tab = (int*)calloc(6, sizeof(int));

…réserve un bloc mémoire utilisable comme un tableau d’entiers de 6 cellules contenant initialement chacune le valeur 0. Ces cellules sont accessibles avec la notation habituelle tab[0], tab[1], … tab[5].

Exercice de découverte E.dec.x5

Donnez les lignes de code permettant de créer un tableau dynamique de double de taille 10 initialisé avec des valeurs 0.0

"Réponse"

    double* t1 = (double*)calloc(10,sizeof(double));

Comme la valeur double 0.0 est constituée d’octets 0, le tableau dynamique est initialisé avec des valeurs 0.0.

Exercice de découverte E.dec.x6

Donnez les lignes de code permettant de créer un tableau dynamique de double de taille 10 initialisé avec des valeurs 1.0.

"Réponse"

    double* t2 = (double*)malloc(10*sizeof(double));
    for(int i=0; i<10; i++) t2[i] = t1.0;

Il aurait été dommage d’utiliser calloc, qui prend du temps à remplir le bloc de 0, alors qu’immédiatement après on va remplie le tableau dynamique avec des valeurs 1.0.

E.dec2 : Gestion de la mémoire

Prérequis

Partie C et section précédente

Objectif

Utiliser de manière rationnelle la mémoire en fonction des besoins

Dans la section précédente, nous avons vu comment créer des tableaux dynamiques. Mais pour ne pas gaspiller de la mémoire, il est important de libérer tout bloc mémoire qui n’est plus utilisé.

On peut présenter les choses de la manière suivante :

À chaque fois qu’un bloc mémoire est réservé par un appel à calloc ou malloc, on contracte une dette mémoire.
Cette dette doit être remboursée en libérant chaque bloc ayant été réservé.

Moyen

La fonction free

Tout bloc mémoire réservé avec calloc ou malloc doit être libéré avec free. Un bloc ne doit être libéré qu’une seule fois. Dans la suite, une tentative d’utiliser free à mauvais escient, comme par exemple avec une adresse ne correspondant pas à un bloc réservé dans le tas ou à un bloc déjà libéré, sera appelée accident mémoire. Ce type de situation provoque souvent un plantage du programme.

void free( void* pointer );

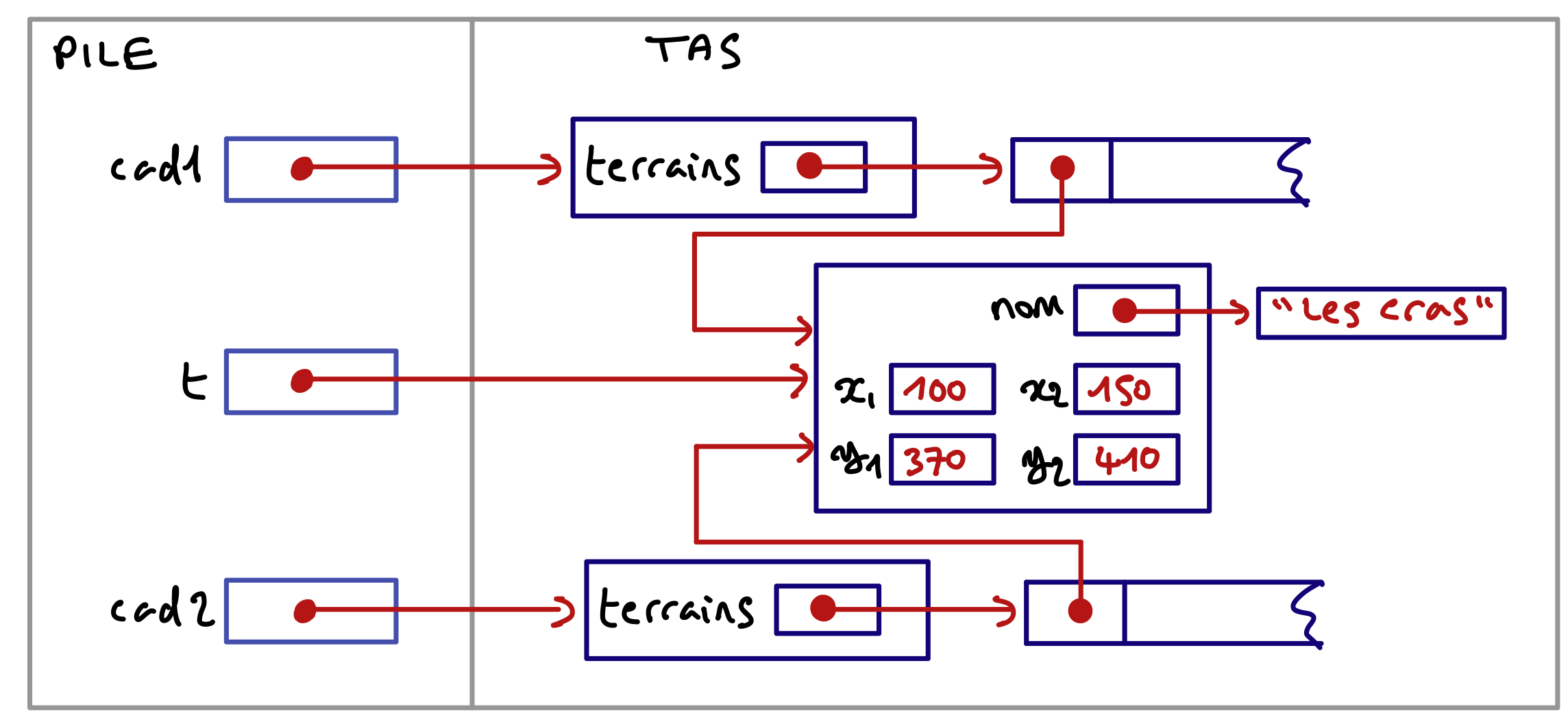
Observons cet exemple d’utilisation de la fonction concat définie dans la section précédente.

int main()
{
    char* s = concat("Tim ", "et Tom ");    // Ligne A
    s = concat(s, "sont sur un bateau.\n"); // Ligne B
    printf("%s\n", s);
    return 0;
}

Chaque concat réserve un bloc mémoire dans le tas, mais aucun de ces blocs n’est libéré explicitement. On a ce qu’on appelle une fuite mémoire. Les blocs sont automatiquement libérés à l’issue de l’exécution du programme, mais les bonnes pratiques de programmation imposent qu’ils soit libérés avant la fin de l’exécution, par utilisation de free.

Avant de corriger notre programme, examinons ce qui se passe en mémoire après l’exécution de la ligne A et après l’exécution de la ligne B.

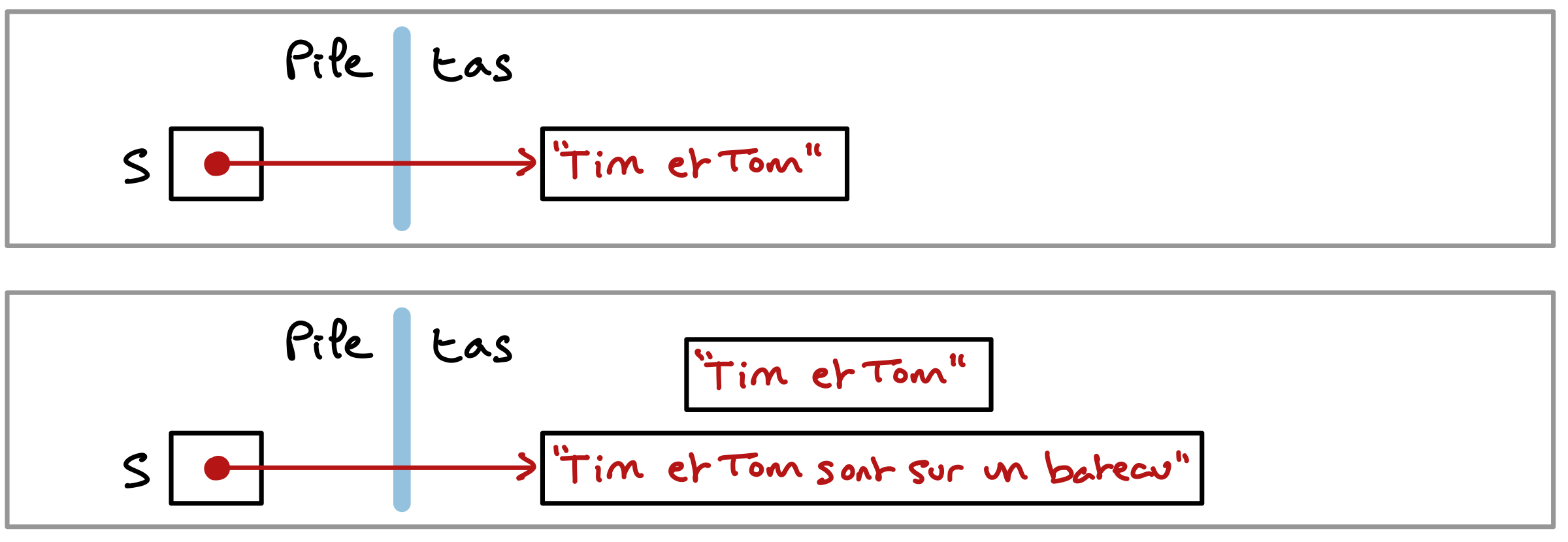
On voit que le premier bloc, qui contient la chaîne "Tim et Tom ", n’a pas été libéré avant que l’adresse du deuxième soit placée dans la variable s. En plus, l’adresse de ce bloc a été perdue, écrasée dans s par celle du nouveau bloc, il ne pourrait donc plus être libéré par free, même si on le voulait. On dit qu’il y a une fuite mémoire lorsqu’un bloc mémoire est réservé dans le tas et n’est jamais libéré par free.

Voici la bonne manière de procéder pour obtenir le même résultat, c’est à dire une chaîne obtenue par la concaténation de "Tim ", "et Tom " et "sont sur un bateau" pointée par s, qui est affichée à l’écran.

int main()
{
    char* s = concat("Tim ", "et Tom ");
    char* t = concat(s, "sont sur un bateau.\n");
    free(s);
    printf("%s\n", t);
    free(t);
    return 0;
}

La première chaîne produite par concat est pointée par s. On doit en garder l’adresse pour pouvoir libérer ultérieurement la mémoire qu’elle occupe dans le tas. On place donc le résultat du deuxième appel de concat dans une nouvelle variable t. On peut libérer le premier bloc, puis utiliser le deuxième, pointé par t. Une fois qu’on en a plus besoin on libère la mémoire qu’il occupe dans le tas.

Exercice de découverte E.dec.x7

Tentez d’identifier le problème dans le programme suivant.

int main()
{
    char* s = malloc(10 * sizeof(char)); // Ligne A
    s = "Bonjour";                       // Ligne B
    printf("%s\n", s);                   // Ligne B
    free(s);                             // Ligne C
}

"Réponse"

On a une fuite mémoire et un accident mémoire. Après exécution de la ligne A, la variable s pointe un bloc mémoire réservé dans le tas. Mais immédiatement après, en ligne B, la variable s reçoit l’adresse d’une chaîne située dans la zone mémoire réservée aux constantes.

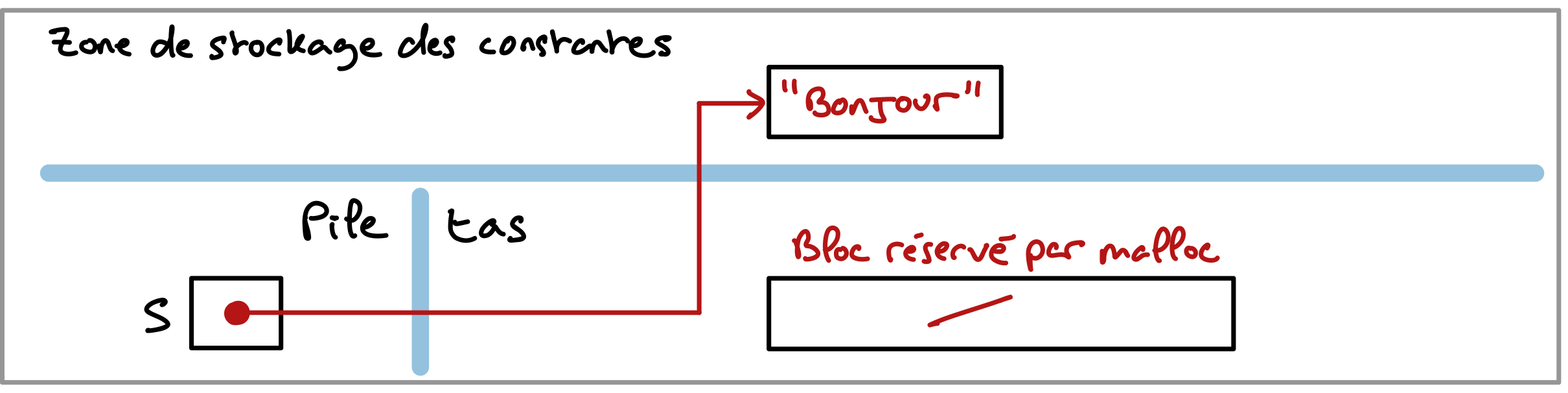
L’instruction s = "Bonjour" ne copie pas "Bonjour" dans le bloc mémoire désigné par s. Pour celà il faudrait utiliser strcpy. Elle copie l’adresse de la chaîne "Bonjour" dans la variable s. La ligne B s’exécute sans problème et affiche "Bonjour", mais la ligne C tente de libérer un bloc mémoire qui n’est pas dans le tas et n’est pas celui réservé par malloc. On a donc accident mémoire. Et comme le bloc réservé par malloc ‘est pas libéré par un appel à free, on a une fuite mémoire.

Voici une version correcte du programme :

int main()
{
    char* s = malloc(10 * sizeof(char)); // Ligne A
    strcpy(s, "Bonjour");                // Ligne B
    printf("%s\n", s);                   // Ligne B
    free(s);                             // Ligne C
}

Bonus

Changer la taille d’un tableau avec realloc

La fonction standard realloc permet de modifier la taille d’un bloc déjà réservé. Seuls les bloc réservés dans le tas peuvent être redimensionnés. Redimensionner un bloc ne change pas la dette mémoire associée. Le bloc devra être libéré, une seule fois, par un appel de la fonction free.

void* realloc( void* pointer, size_t memorySize );

Le premier paramètre est l’adresse du bloc à redimensionner. Si sa valeur est NULL, alors realloc réserve un nouveau bloc, comme le ferait malloc. Le deuxième paramètre est la nouvelle taille du bloc. Elle peut être plus petite ou plus grande que la taille précédente.

Attention, cette opération peut déplacer le bloc et donc changer son adresse. La valeur de retour est la nouvelle adresse du bloc. Si le bloc est déplacé, sont ancien contenu est recopié au nouvel emplacement.

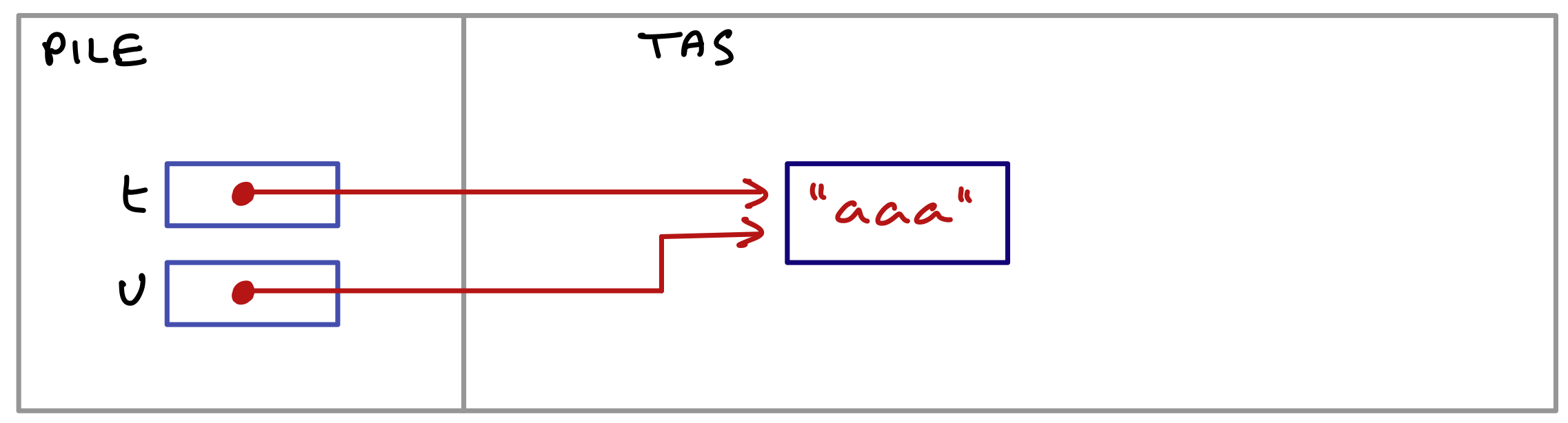
Cet exemple montre comment on utilise realloc pour augmenter la taille d’un bloc.

int main()
{
    char* s = malloc(4*sizeof(char)); // Ligne A
    strcpy(s, "aaa");                 // Ligne B
    s = realloc(s, 7*sizeof(char));   // Ligne C
    strcat(s, "bbb");                 // Ligne D
    printf("%s\n", s);   
    free(s);                          // Ligne E
}

En ligne A, on réserve un bloc mémoire dans lequel est recopié en ligne B la chaîne "aaa". On note que ce bloc doit avoir une taille permettant de stocker 4 caractères, en comptant le marqueur de fin.

En ligne C, on augmente la taille du bloc pointé par s, de manière à pouvoir concéténer, en ligne D, la chaîne "bbb" à celle initialement contenue dans le bloc.

En ligne E, la mémoire occupée par le bloc est libérée.

Exercice de découverte E.dec.x8

Voici une variante du programme précédent qui pose problème. Identifiez s’il y a fuite ou accident mémoire et expliquez pourquoi.

int main()
{
    char* s = malloc(4*sizeof(char));     // Ligne A
    strcpy(s, "aaa");                     // Ligne B
    char* t = realloc(s, 7*sizeof(char)); // Ligne C
    strcat(s, "bbb");                     // Ligne D
    printf("%s\n", t);   
    free(s);                              // Ligne E
    free(t);                              // Ligne F
}

"Réponse"

Deux scénarios sont envisageables et conduisent tous les deux à un accident mémoire.

Soit realloc ne change pas l’adresse du bloc. Dans ce cas, les variables t et s pointent le même bloc, qui sera détruit deux fois. On a donc un accident mémoire.

Soit la réallocation change l’adresse du bloc, alors t pointe le nouvel emplacement et free(t) libérera correctement la mémoire. Mais s pointera l’ancien emplacement où ne se trouve plus de bloc réservé. L’appel free(s) provoquera un accident mémoire.

E.dec3 : Tableau dynamique à 2 dimensions

Prérequis

Parties C et D et section précédentes de cette partie E.

Objectif

Exploiter des tableaux à 2 dimensions situé dans le tas

Jusqu’à maintenant, nous n’avons utilisé que des tableau à une dimension. Il existe plusieurs manières de gérer en C des tableaux à plusieurs dimensions. L’approche native consiste à représenter de tels tableaux par un seul bloc mémoire. Elle est compliquée et manque de souplesse. Nous ne l’aborderons pas dans cet enseignement. Nous allons adopter une approche plus moderne, comparable à celle utilisée par le langage Java.

Moyen

Utiliser un tableau de pointeurs sur des tableaux

Nous allons présenter le principe utilisé avec un exemple dans lequel on représente des matrices carrées de dimension 3 qui pourraient être utilisées pour modéliser des transformations géométriques.

Pour éviter d’utiliser une constante numérique littérale et pour pouvoir modifier facilement la dimension de nos matrices, nous définissions la constante :

#define DIM 3

Voici la représentation en mémoire d’un tableau de 3 lignes et 3 colonnes.

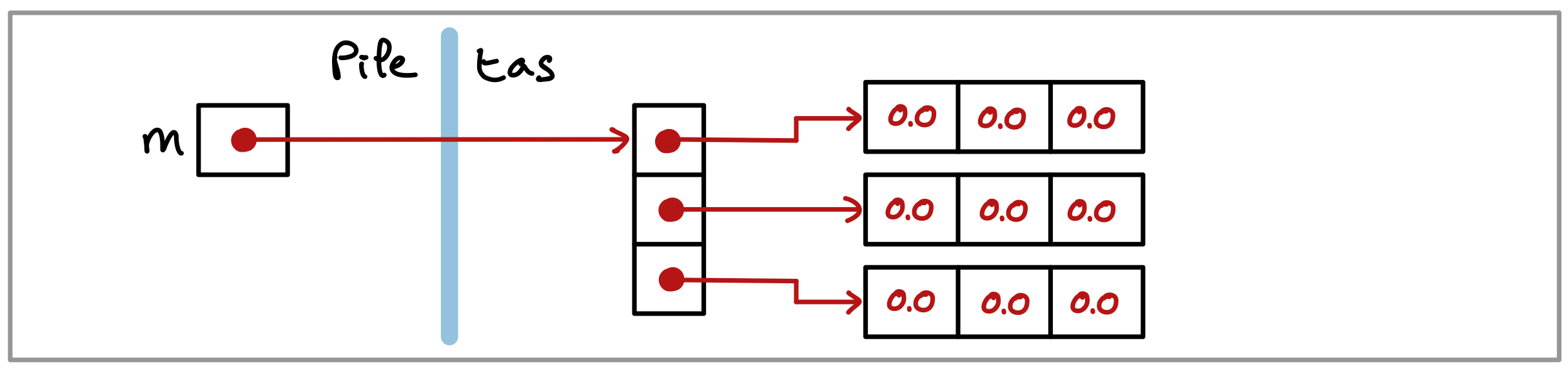
La variable m désigne un tableau dont chaque cellule pointe un tableau dont chaque cellule contient une valeur de type double.

Les valeurs située dans le tableau désigné par m sont de type double*, donc m doit être de type double**. Ce premier tableau doit être réservé par la ligne :

double** mat = (double**)malloc(DIM*sizeof(double*));

Chaque cellule de ce tableau désigne une ligne du tableau 2D, qui est elle même représentée par un tableau de double. Donc par exemple pour créer la première ligne il faut écrire :

mat[0] = (double*)calloc(DIM, sizeof(double));

La création d’un tableau de 3 x 3 nécessite donc la réservation de 4 blocs mémoire dans le tas. Il est judicieux de regrouper toutes les opérations nécessaires dans une fonction.

double** creeMatrice()
{
    double** mat = (double**)malloc(DIM*sizeof(double*));
    for(int i=0; i<DIM; i++)
    {
        mat[i] = (double*)calloc(DIM, sizeof(double));
    }
    return mat;
}

La fonction creeMatrice réalise la création d’une matrice carrée de dimension DIM dont les valeurs, de type double, sont initialisées à 0.0.

La valeur située en ligne i et colonne j est dans la cellule mat[i][j]. En effet, mat[i] est un pointeur qui désigne le tableau représentant la ligne i, et en vertu de la correspondance entre tableaux et pointeurs, mat[i][j] est la cellule d’indice j de cette ligne.

Exercice de découverte E.dec.x9

Définissez la fonction…

void afficheMatrice(double** mat);

…qui affiche la matrice désignée par mat. Chaque valeur doit être affichée au format %.02f. Les valeurs de chaque ligne doivent être séparées par des espaces.

"Réponse"

void afficheMatrice(double** mat)
{
    for(int i=0; i<DIM; i++)
    {
        for(int j=0; j<DIM; j++)
        {
            printf(" %.02f", mat[i][j]);
        }
        printf("\n");
    }
}

Exercice de découverte E.dec.x10

Réalisez une fonction main qui crée une matrice en utilisant la fonction creeMatrice et qui l’affiche en utilisant la fonction afficheMatrice.

"Réponse"

int main()
{
    double** m = creeMatrice();
    afficheMatrice(m);
}

Pour libérer correctement la mémoire occupée par une matrice, il faut libérer tous les blocs mémoires qui la constituent. Pour une matrice de 3 x 3, cela suppose 4 appels à free. Pour faciliter cette tâche, il est judicieux de définir une fonction :

void detruitMatrice(double** m)
{
    for(int i=0; i<DIM; i++)
    {
        free(m[i]);
    }
    free(m);
}

Bonus

Simplifier les notation en définissant un type.

Les notations avec plusieurs étoiles peuvent paraître un peu lourdes. Il est possible de les alléger en définissant de nouveaux type à l’aide de typedef. Par exemple, si on écrit…

typedef double** matrice;

…on définit un type matrice qui est équivalent à double**. Voici le code des fonctions de création, affichage et destruction de matrices utilisant ce type :

#define DIM 3

typedef double** matrice;

matrice creeMatrice()
{
    matrice mat = (matrice)malloc(DIM*sizeof(double*));
    for(int i=0; i<DIM; i++)
    {
        mat[i] = (double*)calloc(DIM, sizeof(double));
    }
    return mat;
}

void afficheMatrice(matrice mat)
{
    for(int i=0; i<DIM; i++)
    {
        for(int j=0; j<DIM; j++)
        {
            printf(" %.02f", mat[i][j]);
        }
        printf("\n");
    }
}

void detruitMatrice(matrice m)
{
    for(int i=0; i<DIM; i++)
    {
        free(m[i]);
    }
    free(m);
}

Exercice de découverte E.dec.x11

Définissez une fonction main qui crée la matrice :

\[ \begin{pmatrix}
1.0 & 0.0 & 0.0\\
0.0 & 1.0 & 0.0\\
0.0 & 0.0 & 1.0
\end{pmatrix}
\]

Puis l’affiche et la détruit.

"Réponse"

int main()
{
    matrice m = creeMatrice();
    m[0][0] = 1.0; m[1][1] = 1.0; m[1][1] = 1.0; 
    afficheMatrice(m);
    detruitMatrice(m);
    return 0;
}

L’activité est terminée. Vous devez évaluer votre réussite de cette activité par une valeur entre 1 et 4.

Vous n’avez presque rien compris et échoué à plus de la moitié des exercices de découverte.
Vous estimez avoir compris une partie des explications et vous avez réussi au moins la moitié des exercices de découverte, mais certaines notions sont encore floues.
Vous estimez avoir bien compris les explications et vous avez réussi presque tous les exercices de découverte, mais certaines notions abordées étaient nouvelles et vous penser avoir besoin d’un entrainement pour bien les assimiler et être en mesure de les utiliser en pratique.
Vous connaissiez déjà tout ce qui a été présenté (sauf peut être quelques détails) et il ne sera pas nécessaire que vous reveniez sur ces notions.

Si votre score est 1 ou 2, vous devrez refaire cette activité rapidement, mais après au moins une nuit de sommeil, avant de passer aux activités suivantes. Si votre score est 3 ou 4, vous devez faire les activités suivantes et il ne sera pas nécessaire de revenir sur cette activité, à part pour rechercher des informations utiles pour d’autres activités.

Activité d’entraînement E.ent

Cette activité est essentielle. C’est grâce à elle que vous apprendrez vraiment à comprendre et utiliser les notions vues précédemment. Elle se décompose en plusieurs itérations : ent1, ent2, etc.

Vous devez réaliser au moins une itération et évaluer votre niveau de réussite par une valeur entre 1 et 4 selon les critères habituels. L’itération que vous avez traité le plus récemment est appelée itération courante. On appelle itération suivante celle qui suit l’itération courante, excepté si l’itération courante est la dernière disponible, auquel cas l’itération suivante est la première itération.

Si le résultat est 1, vous devrez traiter à nouveau l’activité de découverte précédente, en laissant passer au moins une nuit, avant de revenir à cette activité d’entraînement en réalisant à nouveau l’itération courante. Vous devez aussi essayer d’identifier les points de blocage et demander à votre enseignant de vous aider à les surmonter.

Si le résultat est 2, vous devrez d’abord comprendre ce qui vous a conduit à des erreurs et / ou ce qui vous a bloqué. Si vous avez des doutes, des difficultés, essayez de trouver les réponses dans les présentations et explication de l’activité de découverte précédente et demandez toute l’aide nécessaire à votre enseignant. Ensuite, vous devrez réaliser l’itération suivante de l’activité d’entraînement actuelle après un délai d’au moins deux jours et d’au plus une semaine.

Si le résultat est 3, vous devrez revenir traiter l’itération suivante après un délai de plusieurs semaines.

En traitant les exercices, vous devrez considérer que les paramètres des fonctions ont des valeurs correctes. Il ne vous est pas demandé de vérifier si certaines valeurs sont aberrantes au regard de ce que demande l’énoncé. Par exemple, si un paramètre doit être positif pour que le traitement demandé soit possible, vous considérerez que la fonction sera appelée avec une valeur positive de ce paramètre.

Vous pouvez utiliser un ordinateur pour tester vos solutions et les corriger en cas de comportement inattendu. C’est même recommandé, à condition de commencer par réfléchir avant de vous jeter sur le clavier. Si vous pensez avoir une solution différente de celle proposée, ce qui peut arriver souvent, vous ne devez en aucun cas rester dans le doute. Vous devez vérifier si votre solution est correcte ou non, soit en testant votre solution avec un ordinateur, soit en demandant à une personne enseignante.

Itération E.ent1

Exercice d’entrainement E.ent1.1

Définissez une fonction…

char* randStr(const char* caracteres, int n);

…qui produit une chaîne de n caractères tirés aléatoirement dans la chaîne caracteres. La chaîne produite doit être située dans le tas. Par exemple, la ligne…

char* s = randStr("abc", 4);

…produit une chaîne de 4 caractères tirés aléatoirement parmi les caractères a, b et c. Une telle chaîne pourrait par exemple être "abba", ou "cabc".

"Indice"

char* randStr(const char* caracteres, int n)
{
    char* out = (char*)malloc((n+1)*sizeof(char)); // Ligne A
    int nchars = strlen(caracteres);               // Ligne B
    // À compléter
    return out;                                    // Ligne C
}

Voici le début du code de la fonction. La ligne A réserve le bloc mémoire qui contiendra la chaîne produite. Attention, la chaîne doit contenir n caractères plus un marqueur de fin. La ligne B détermine la longueur de la chaîne contenant les caractères éligibles pour être placés dans le chaîna à produire. La ligne C retourne l’adresse de la chaîne produite après qu’elle ait été remplie avec des caractères tirés aléatoirement dans la chaîne caracteres, sans oublier le marqueur de fin.

"Réponse"

char* randStr(const char* caracteres, int n)
{
    char* out = (char*)malloc((n+1)*sizeof(char));
    int nchars = strlen(caracteres);
    for(int i=0; i<n; i++)
    {
        out[i] = caracteres[rand()%nchars];
    }
    out[n] = 0;
    return out;
}

Définissez une fonction main qui crée (en utilisant randStr) une chaîne aléatoire constituée de 6 lettre majuscules tirées au hasard dans l’alphabet, puis qui affiche cette chaîne. La mémoire réservée dans le tas doit être libérée après utilisation.

"Réponse"

int main()
{
    srand(time(NULL));
    char* s = randStr("ABCDEFGHIJKLMNOPQRSTUVWXYZ", 6);
    printf("%s\n", s);
    free(s);
}

Exercice d’entrainement E.ent1.2

Donnez les lignes de code permettant de réaliser les actions suivantes :

Créer dans la pile un tableau d’entiers de taille 5 initialisé avec les valeurs 1,2,3,4,5.
Créer dans le tas un tableau d’entiers de taille 5 non initialisé.
Recopier les valeurs du premier tableau dans le deuxième.
Placer la valeur 12 dans la cellule d’indice 2 du deuxième tableau.
Libérer la mémoire ayant été réservée dans le tas.

"Réponse"

    int t[] = {1,2,3,5,4};
    int* w = (int*)malloc(5 * sizeof(int));
    for(int i=0; i<5; i++) w[i] = t[i];
    w[2] = 12;
    free(w);

Exercice d’entrainement E.ent1.3

Cet exercice est un bon entraînement pour ce qui concerne les pointeurs, tableaux et gestion dynamique de la mémoire. Mais pour une implémentation plus professionnelle du concept, il est préférable d’utiliser en plus la notion de structure, qui sera présentée dans la partie suivante. Il ne faut donc pas considérer l’implémentation proposée ici comme une solution définitive, mais comme une étape d’apprentissage.

On reprend le tableau 2D définit par le type matrice présenté précédemment.

#define DIM 3

typedef double** matrice;

matrice creeMatrice()
{
    matrice mat = (matrice)malloc(DIM*sizeof(double*));
    for(int i=0; i<DIM; i++)
    {
        mat[i] = (double*)calloc(DIM, sizeof(double));
    }
    return mat;
}

void afficheMatrice(matrice mat)
{
    for(int i=0; i<DIM; i++)
    {
        for(int j=0; j<DIM; j++)
        {
            printf(" %.02f", mat[i][j]);
        }
        printf("\n");
    }
}

void detruitMatrice(matrice m)
{
    for(int i=0; i<DIM; i++)
    {
        free(m[i]);
    }
    free(m);
}

Vous devez faire une première modification pour représenter, avec un type que nous nommerons tab2Ddouble, des tableaux dont le nombre de lignes est définit par une constante NLIGNES et le nombre de colonnes par une constante NCOLONNES.

#define NLIGNES 2
#define NCOLONNES 3

// À compléter

tab2Ddouble creeTab2D()
{
    // À compléter
}

void afficheTab2D(tab2Ddouble tab)
{
    // À compléter
}

void detruitTab2D(tab2Ddouble tab)
{
    // À compléter
}

"Solution"

#define NLIGNES 2
#define NCOLONNES 3

typedef double** tab2Ddouble;

tab2Ddouble creeTab2D()
{
    tab2Ddouble tab = (tab2Ddouble)malloc(NLIGNES*sizeof(double*));
    for(int i=0; i<NLIGNES; i++)
    {
        tab[i] = (double*)calloc(NCOLONNES, sizeof(double));
    }
    return tab;
}

void afficheTab2D(tab2Ddouble tab)
{
    for(int i=0; i<NLIGNES; i++)
    {
        for(int j=0; j<NCOLONNES; j++)
        {
            printf(" %.02f", tab[i][j]);
        }
        printf("\n");
    }
}

void detruitTab2D(tab2Ddouble tab)
{
    for(int i=0; i<NLIGNES; i++)
    {
        free(tab);
    }
    free(tab);
}

Une personne débutante en programmation C écrit la fonction suivante ayant pour rôle d’échanger les contenus de deux tableaux.

void exgTab2D(tab2Ddouble t1, tab2Ddouble t2)
{
    tab2Ddouble tmp = t1;
    t1 = t2;
    t2 = tmp;
}

Mais la fonction ne remplit pas son rôle. Si on exécute le programme suivant :

int main()
{
    tab2Ddouble tab1 = creeTab2D();
    tab2Ddouble tab2 = creeTab2D();
    tab1[0][0] = 3.0;
    tab2[1][2] = 9.0;
    
    printf("Avant :\n");
    afficheTab2D(tab1);
    printf("\n");
    afficheTab2D(tab2);
    
    exgTab2D(tab1, tab2);
    
    printf("\nAprès :\n");
    afficheTab2D(tab1);
    printf("\n");
    afficheTab2D(tab2);

    return 0;
}

On obtient exactement le même affichage avant et après appel de la fonction. Les tableaux désignés par tab1 et tab2 n’ont pas été échangés. Vous devez menez une enquête afin de trouver une explication du phénomène.

"Réponse"

Quand on appelle exTab2D(tab1, tab2), les valeurs de tab1 et tab2, c’est à dire les adresses des 2 tableaux, sont copiées dans les paramètres t1 et t2 de la fonction. Ce sont ce copies que le fonction échange, ce qui n’affecte pas les contenus des variables tab1 et tab2.

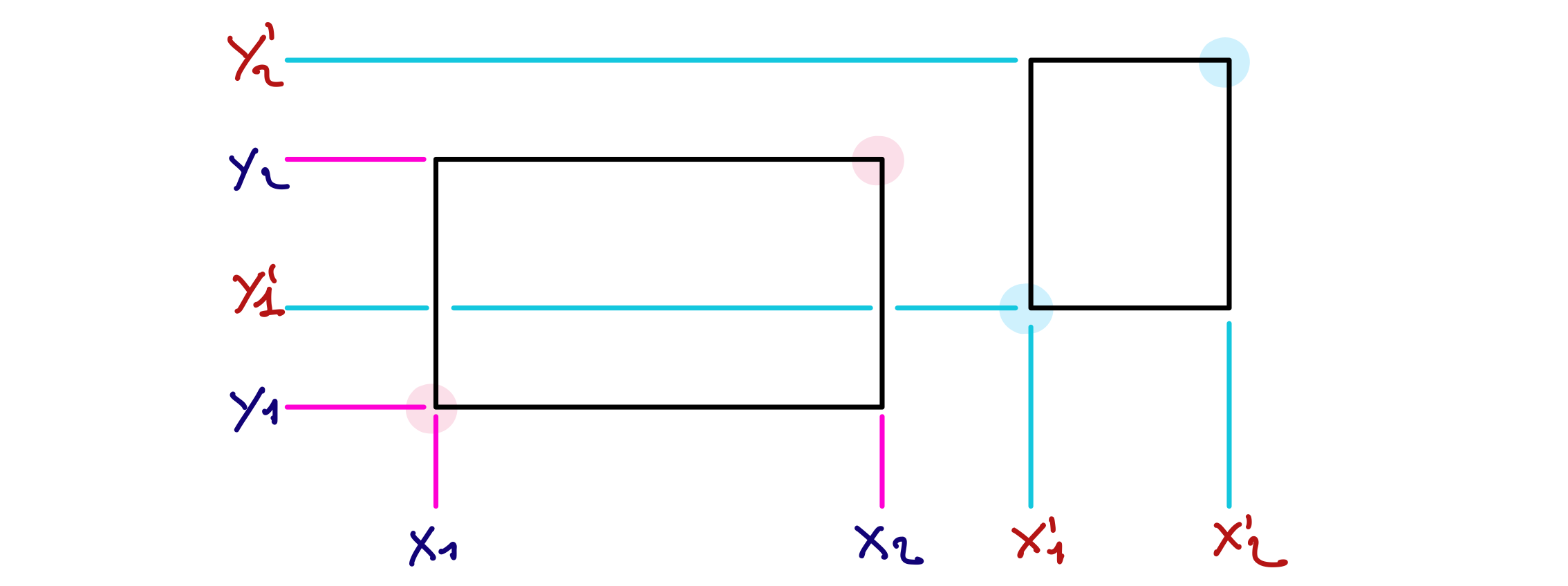
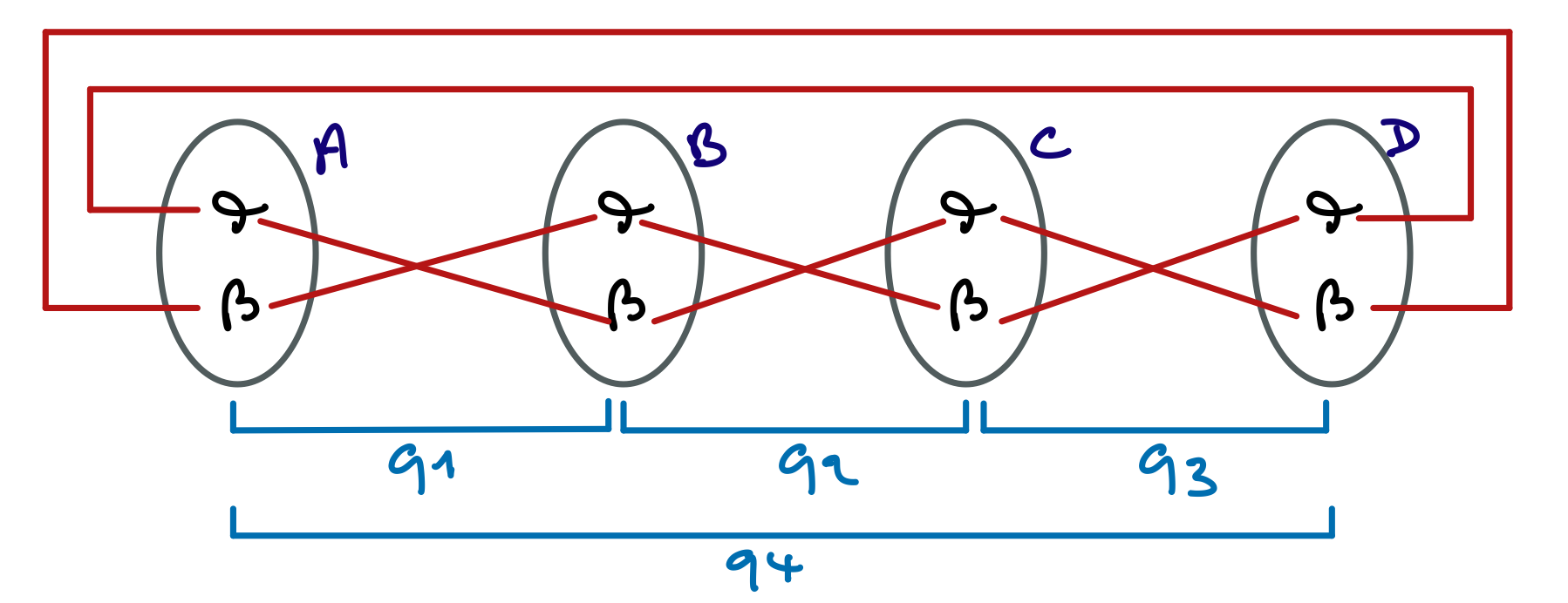
Voici la situation en mémoire au début de l’exécution de la fonction exTab2D.

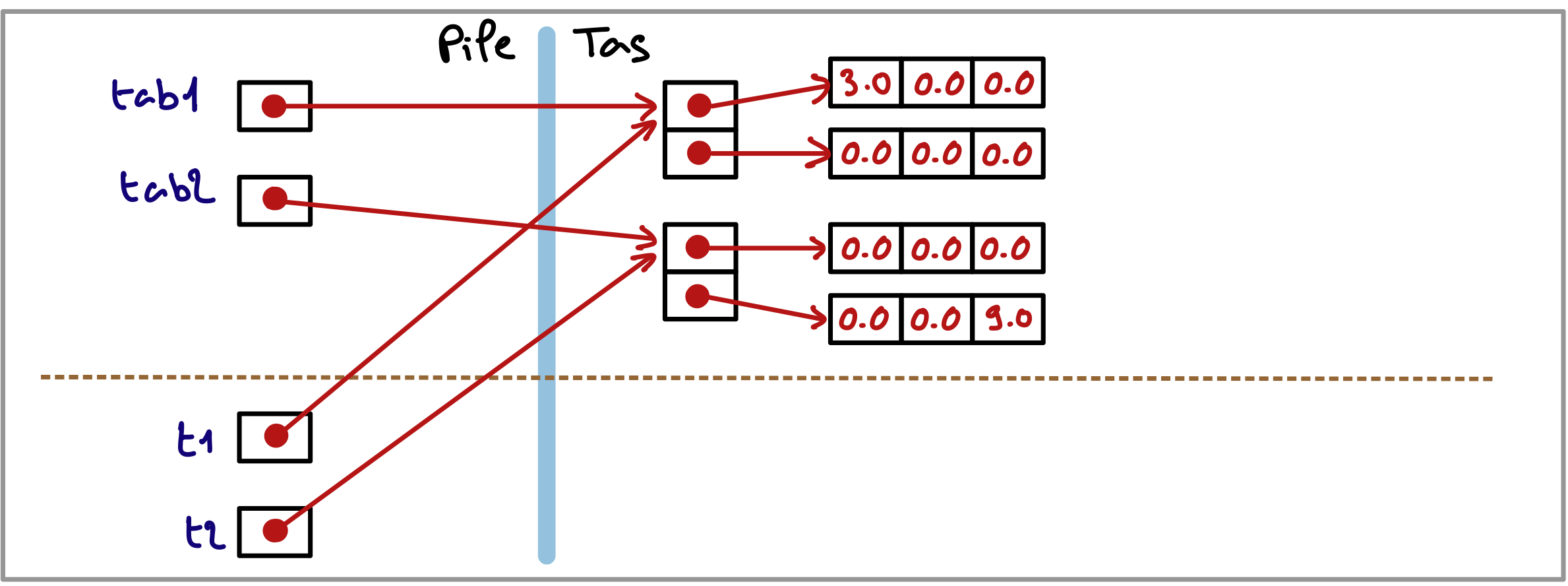
Et voici la situation en mémoire à la fin de l’exécution de cette fonction.

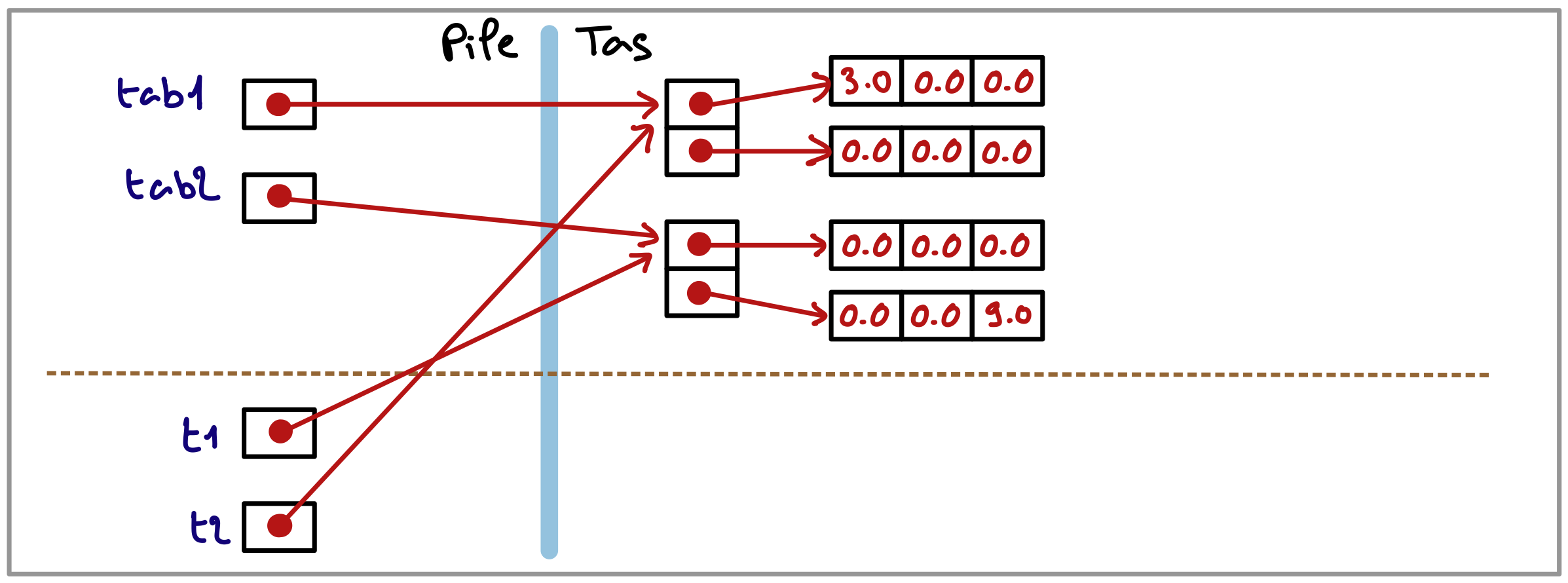
Vous devez trouver un moyen de coder cette fonction de manière à ce que les contenus des tableaux soient effectivement échangés.

"Indice1"

On pourrait échanger chaque valeur du premier tableau avec la valeur située en même position dans le deuxième, mais une solution plus rapide est d’échanger le pointeur sur chaque ligne d’un des tableau avec le pointeur sur la ligne ayant la même position dans l’autre.

"Solution"

void exgTab2D(tab2Ddouble t1, tab2Ddouble t2)
{
    for(int i=0; i<NLIGNES; i++)
    {
        double* tmp = t1[i];
        t1[i] = t2[i];
        t2[i] = tmp;
    }
}

Définissez une variante qui accepte en paramètres les adresses des variables désignant les tableaux à échanger :

void exgTab2D(tab2Ddouble* t1, tab2Ddouble* t2);

Donnez la modification à faire dans la fonction main précédente pour appeler correctement la nouvelle fonction d’échange.

"Solution"

void exgTab2D(tab2Ddouble* t1, tab2Ddouble* t2)
{
    tab2Ddouble tmp = *t1;
    *t1 = *t2;
    *t2 = tmp;
}

Ce sont les valeurs pointées par t1 et t2 qu’il faut échanger, et on accède à ces valeurs par l’opérateur de "dépointage" *.

Dans la fonction main, il faut remplacer la ligne…

exgTab2D(tab1, tab2);

…par la ligne :

exgTab2D(&tab1, &tab2);

En effet, ce sont les adresses des variables tab1 et tab2 qui doivent être passées en arguments.

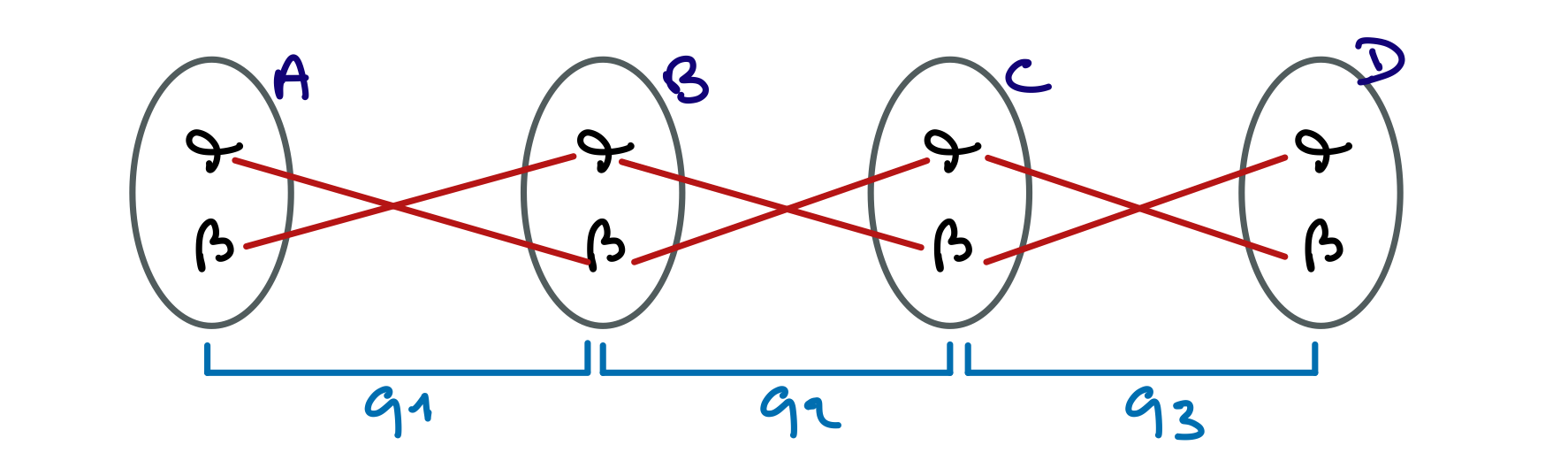
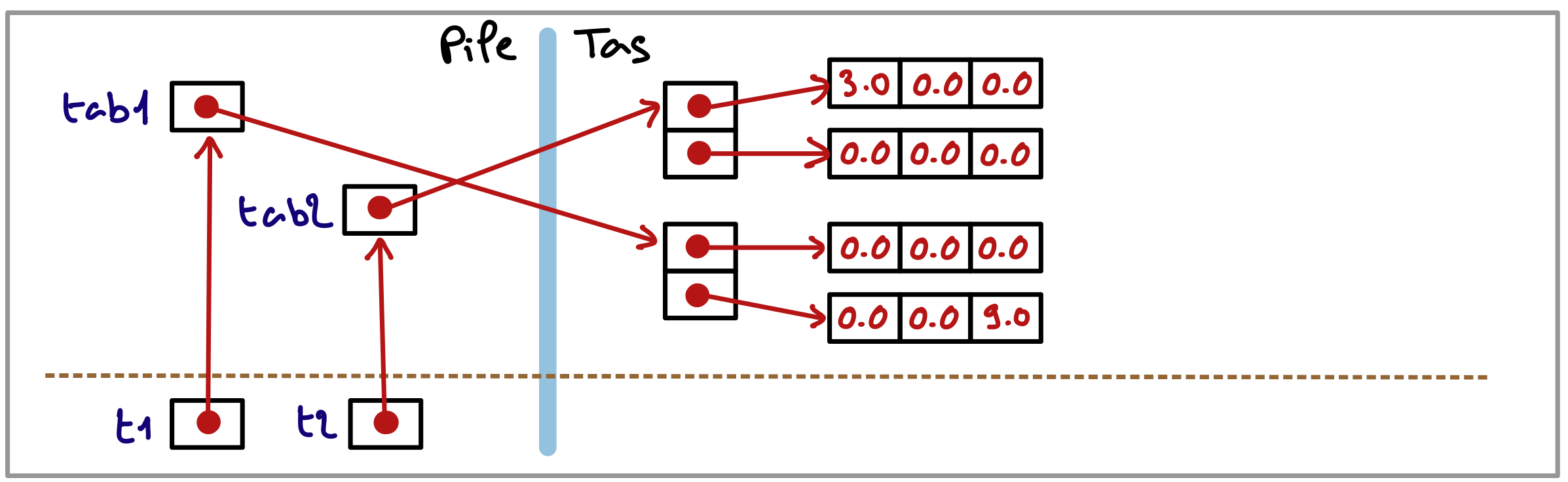
Dessinez la situation en mémoire au début et à la fin de l’exécution de cette nouvelle variante de la fonction appelée par main.

"Réponse"

Au début de l’exécution :

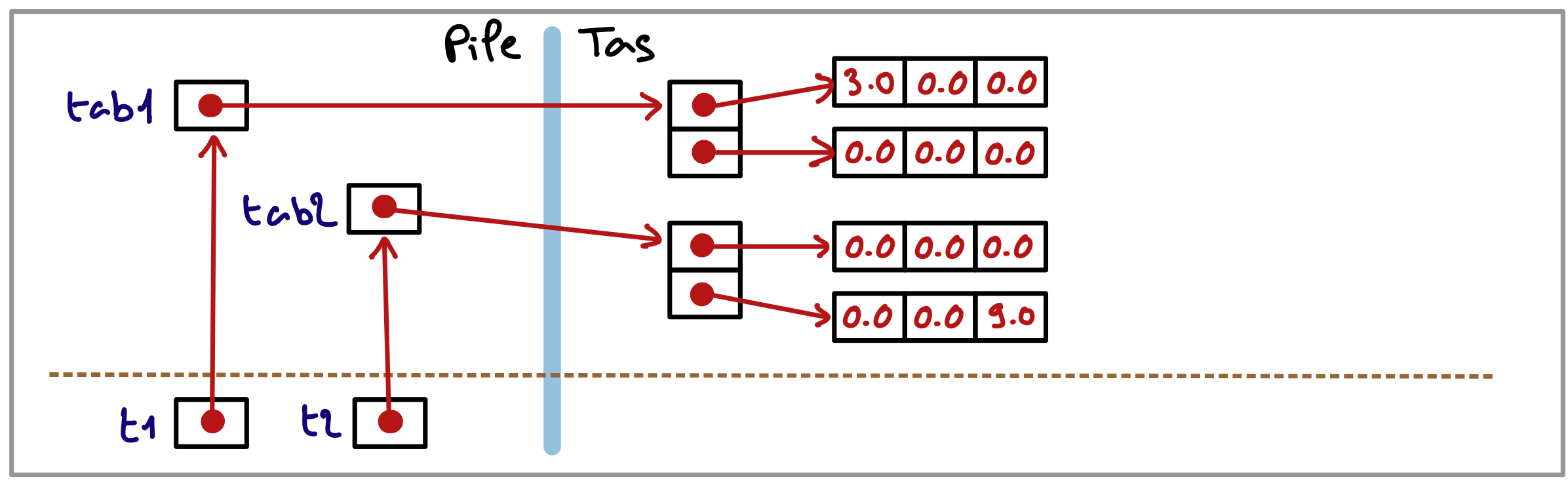
À la fin de l’exécution :

Itération E.ent2

Exercice d’entrainement E.ent2.1

Définissez une fonction…

char* cloneStr(const char* s);

…qui produit une chaîne située dans le tas, strictement identique à la chaîne désignée par s, mais complètement indépendante en mémoire (une modification de la chaîne produite ne doit pas affecter la chaîne ayant servi de modèle, et réciproquement).

"Indice"

char* cloneStr(const char* s)
{
    int n = strlen(s);
    char* out = (char*)malloc((n+1)*sizeof(char));
    // À compléter
}

"Réponse"

char* cloneStr(const char* s)
{
    int n = strlen(s);
    char* out = (char*)malloc((n+1)*sizeof(char));
    strcpy(out, s);
    return out;
}

Définissez une fonction main qui crée (en utilisant cloneStr) une copie de la chaîne "Bonjour", puis qui affiche cette chaîne. La mémoire réservée dans le tas doit être libérée après utilisation.

"Réponse"

int main()
{
    char* s = cloneStr("Bonjour");
    printf("%s\n", s);
    free(s);
}

Exercice d’entrainement E.ent2.2

Donnez les lignes de code permettant de réaliser les actions suivantes :

Créer dans le tas un tableau d’entiers de taille 5 dont les 4 premières cellules contiennent la valeur 0 et la dernière cellule contient la valeur 2.
Créer dans la pile tableau d’entiers de taille 5 non initialisé.
Recopier les valeurs du premier tableau dans le deuxième.
Libérer la mémoire ayant été réservée dans le tas.

"Réponse"

    int* t = (int*)calloc(5, sizeof(int));
    t[4] = 2;
    int w[5];
    for(int i=0; i<5; i++) w[i] = t[i];
    free(t);

Exercice d’entrainement E.ent2.3

Cet exercice est un bon entraînement pour ce qui concerne les pointeurs, tableaux et gestion dynamique de la mémoire. Mais pour une implémentation plus professionnelle du concept, il est préférable d’utiliser en plus la notion de structure, qui sera présentée dans la partie suivante. Il ne faut donc pas considérer l’implémentation proposée ici comme une solution définitive, mais comme une étape d’apprentissage.

On définit la constante et le type suivants :

#define SIZE 3
typedef char** tabstr;

Le type tabstr représente un tableau de chaînes de caractères de taille SIZE dont certaines cellules peuvent être vides. Une cellule vide contient la valeur NULL, alors qu’une cellule non vide contient un pointeur sur char désignant une chaîne stockée dans le tas.

Les fonctions suivantes permettent l’utilisation de tableaux de chaîne de type tabstr.

// Crée un tableau de SIZE cellules vides.
tabstr creeTabstr();

// Place une copie de la chaîne désignée par str dans la cellule i
// du tableau désigné par tab.
void assigne(tabstr tab, int i, char* str);

// Affiche le contenu du tableau désigné par tab.
// Les cellules vides sont représentées par ---
void affiche(tabstr tab);

// Libère toute la mémoire occupée par le tableau désigné par tab.
void detruit(tabstr tab);

Voici un exemple de mise en oeuvre de ces fonctions :

int main()
{
    tabstr t = creeTabstr();
    assigne(t,0,"Tim");
    assigne(t,1,"Tom");
    assigne(t,0,"Anne");
    affiche(t);
    detruit(t);
    return 0;
}

L’exécution de main produit l’affichage :

Anne
Tom
---

Dessinez la situation en mémoire juste après l’exécution de la fonction affiche appelé par main.

"Réponse"

Donnez les définitions des fonctions suivantes :

creeTabstr
affiche
assigne
detruit

Vous devez prêter une attention particulière à éviter les fuites et accidents mémoire. Lorsqu’on crée un tableau dynamique de pointeurs avec calloc, ces cellules contiennent toutes la valeur NULL, qui est représentée en mémoire par des octets ayant la valeur 0.

Pour coder correctement les fonctions affiche, assigne et detruit, il faut bien distinguer le cas d’une cellule contenant NULL d’une cellule pointant une chaîne préalablement assignée.

"Réponse1"

tabstr creeTabstr()
{
    tabstr out = (tabstr)calloc(SIZE, sizeof(char*));
    return out;
}

On réserve un bloc mémoire qui sera utilisé comme tableau de SIZE pointeurs de type char*. La fonction calloc initialise le bloc avec des 0, donc les cellules du tableau contiennent NULL.

"Réponse2"

void affiche(tabstr tab)
{
    for(int i=0; i<SIZE; i++)
    {
        if(tab[i]==NULL) printf("---\n");
        else printf("%s\n", tab[i]);
    }
}

Il ne faut pas utiliser printf avec le format %s dans le cas où la cellule contient NULL, mais faire un affichage spécifique dans ce cas.

"Réponse3"

void assigne(tabstr tab, int i, char* str)
{
    if(tab[i] != NULL) free(tab[i]);
    int n = strlen(str);
    tab[i] = (char*)malloc((n+1)*sizeof(char));
    strcpy(tab[i], str);
}

Il faut penser à beaucoup de choses pour coder correctement cette fonction :

Si la cellule à assigner pointe déjà une chaîne, c’est à dire si elle a déjà été préalablement assignée, il faut libérer la mémoire occupée par la chaîne précédente, sinon on aura une fuite mémoire.
Il faut réserver un bloc mémoire pour y placer la copie de la chaîne à assigner à la cellule d’indice i.
La taille du bloc à réserver doit prévoir d’y placer la copie de la chaîne à assigner sans oublier le marqueur de fin.
La copie de la chaîne à assigner dans le bloc destiné à la contenir doit être réalisée par un appel à la fonction strcpy et en aucun cas avec =.

"Réponse4"

void detruit(tabstr tab)
{
    for(int i=0; i<SIZE; i++)
    {
        if(tab[i] != NULL) free(tab[i]);
    }
    free(tab);
}

Il faut libérer la mémoire utilisée pour stocker les chaînes, mais il peut y avoir des cellules vides (contenant NULL), qui ne pointent donc aucune chaîne. Il ne faut jamais appeler free avec NULL en argument, cela provoque un accident mémoire.

Itération E.ent3

Exercice d’entrainement E.ent3.1

Définissez une fonction…

char* addChar(const char* s, char c);

…qui produit une obtenue en ajoutant le caractère c a une copie de la chaîne désignée par s. Par exemple, l’appel addChar("Tim", 'e') retourne l’adresse d’une chaîne "Time" située dans le tas.

"Indice"

char* addChar(const char* s, char c)
{
    int n = strlen(s);
    char* out = (char*)malloc((n+2)*sizeof(char));
    // À compléter
    return out;
}

La partie de la fonction donnée ici réserve le bloc mémoire dans lequel sera placé la chaîne à produire. Il faut prévoir la place pour placer le caractère à ajouter et le marqueur de fin. Il reste à terminer la construction.

"Réponse"

char* addChar(const char* s, char c)
{
    int n = strlen(s);
    char* out = (char*)malloc((n+2)*sizeof(char));
    strcpy(out, s);
    out[n] = c;
    out[n+1] = 0;
    return out;
}

Remarque : la fonction strcat n’est pas utilisable pour concaténer un caractère à une chaîne. Le caractère est ajouté directement dans le tableau représentant la chaîne, à l’emplacement approprié.

Exercice d’entrainement E.ent3.2

Donnez les lignes de code permettant de réaliser les actions suivantes :

Créer dans la pile une chaîne initialisée avec "abcde".
Créer dans le tas un tableau de 6 caractères.
Recopier dans ce tableau la chaîne créée à l’étape 1.
Libérer la mémoire ayant été réservée dans le tas.

"Réponse"

    char t[] = "abcde";
    char* s = malloc(6 * sizeof(char));
    strcpy(s, t);
    free(t);

Activité de consolidation E.top

Réaliser cette activité consiste à traiter un des exercices de consolidation proposés. Si vous réalisez plusieurs fois cette activité, laissez passer au moins une semaine entre chaque itération et traitez à chaque fois un exercice différent.

Exercice de consolidation C.top1

On appelle tableau informé de taille n un tableau d’entiers dont les valeurs sont stockées aux indices 1 à n et la longueur est stockée à l’indice 0. Un tel tableau est donc représenté par un tableau de n+1 cellules de type int. Voici un exemple de tableau de valeur de type int représentant le tableau informé de taille 4 contenant les valeurs 2, 3, 5, 7 :

On définit le type tabinf pour représenter les tableaux informés :

typedef int* tabinf;

Pour rappel, cette notation signifie que l’identificateur tabinf est équivalent à int*. En effet, un tableau informé est représenté par un tableau de valeurs de type int, qui est désigné, en vertu de la correspondance entre pointeurs et tableaux, par un pointeur sur int.

Votre première mission consiste à définir une fonction…

tabinf creeTabinf(int n);

…qui crée un tableau informé situé dans le tas contenant n valeurs 0.

"Réponse"

tabinf creeTabinf(int n)
{
 tabinf out = calloc(n+1, sizeof(int));  // Ligne A
 out[0] = n;                             // Ligne B
 return out;                             // Ligne C
}

En ligne A, un bloc mémoire permettant de stocker n+1 entiers est réservé. Ce bloc est initialisé avec des valeurs 0 et est utilisable comme un tableau classique de valeurs de type int.

En ligne B, la valeur n est placée dans la première cellule du tableau venant d’être créé, puisque ce tableau représente un tableau informé de taille n.

La ligne C retourne l’adresse du tableau informé créé.

Vous devez maintenant définir une fonction…

void printTabinf(tabinf t)

…qui affiche les valeurs d’un tableau informé (pas sa taille) séparées par des espaces.

"Réponse"

void printTabinf(tabinf t)
{
 for(int i=1; i<=t[0]; i++)
 {
     printf(" %d", t[i]);
 }
 printf("\n");
}

Définissez une fonction main qui

Crée un tableau informé de taille 10 contenant des valeurs 0 sauf à l’indice 2 où il y a la valeur 12.
Affiche ce tableau informé avec la fonction printTabinf.
Libère la mémoire utilisée par le tableau.

"Réponse"

int main()
{
 tabinf tab = creeTabinf(10);
 tab[2] = 12;
 printTabinf(tab);
 free(tab);
 return 0;
}

Nous attaquons à présent la partie plus technique de l’exercice. Vous devez définir une fonction…

void agrandit(tabinf* t, int delta);

…qui agrandit un tableau informé en lui ajoutant delta valeurs supplémentaires, toutes initialisées à 0. Vous ne devez pas utiliser (dans cette première version), la fonction realloc. Donc vous devez créer un nouveau tableau plus grand et recopier dedans les valeur de l’ancien, sans oublier de détruire l’ancien ensuite, afin d’éviter toute fuite mémoire.

Il est très important de bien comprendre pourquoi le premier paramètre est de type tabinf*, c’est à dire int**, et ce que cela implique, à savoir que lors de l’appel de la fonction, il faut lui passer en premier argument l’adresse d’une variable de type tabinf.

Voici un exemple de création, puis d’agrandissement d’un tableau informé.

int main()
{
 tabinf tab = creeTabinf(10);
 tab[2] = 12;
 printTabinf(tab);
 agrandit(&tab, 5);
 printTabinf(tab);
 free(tab);
 return 0;
}

Vous devez réfléchir et répondre à la question suivante : Pourquoi une fonction agrandit avec une paramètre de type tabinf (c’est à dire int*) ne pourrait pas permettre de réaliser correctement le travail demandé, à savoir remplacer le tableau informé initialement créé par une plus grand contenant les valeurs du premier et des 0 supplémentaires ?

"Réponse"

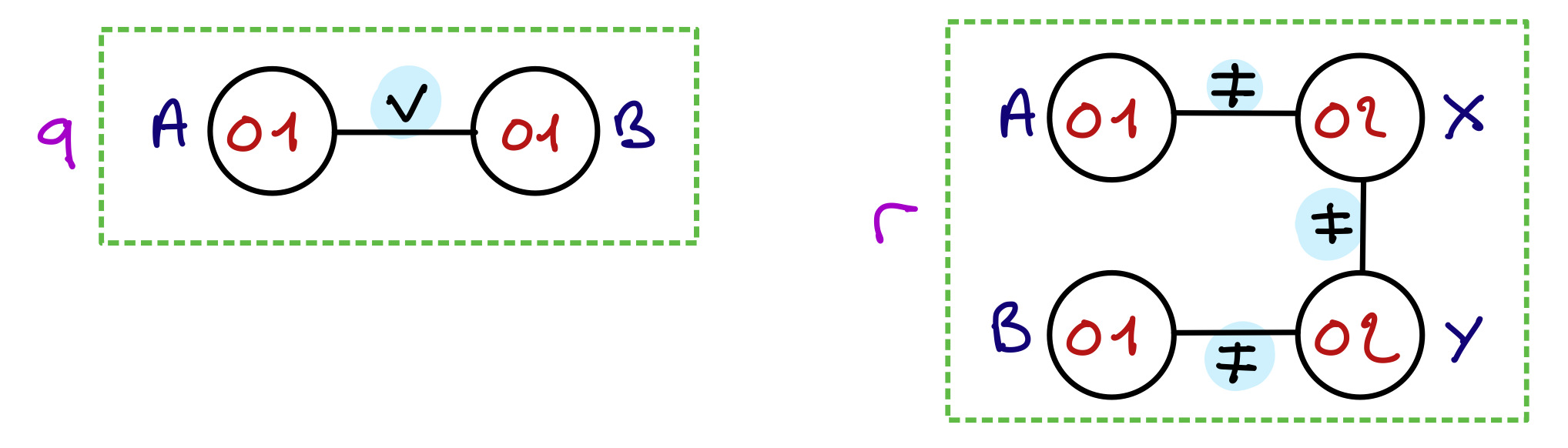
L’agrandissement d’un tableau informé change son adresse mémoire, qui est contenue dans la variable tab. Si on passe cette adresse en argument à la fonction d’agrandissement, c’est une copie de cette adresse qui sera transmise à la fonction. Lors de son exécution, la fonction agrandit va modifier cette copie d’adresse, mais cela ne modifiera pas contenu de la variable tab qui continuera de pointer sur l’ancien tableau ou sur son fantôme si la mémoire qu’il occupait a été libérée.

Voici une illustration en image du "scénario catastrophe".

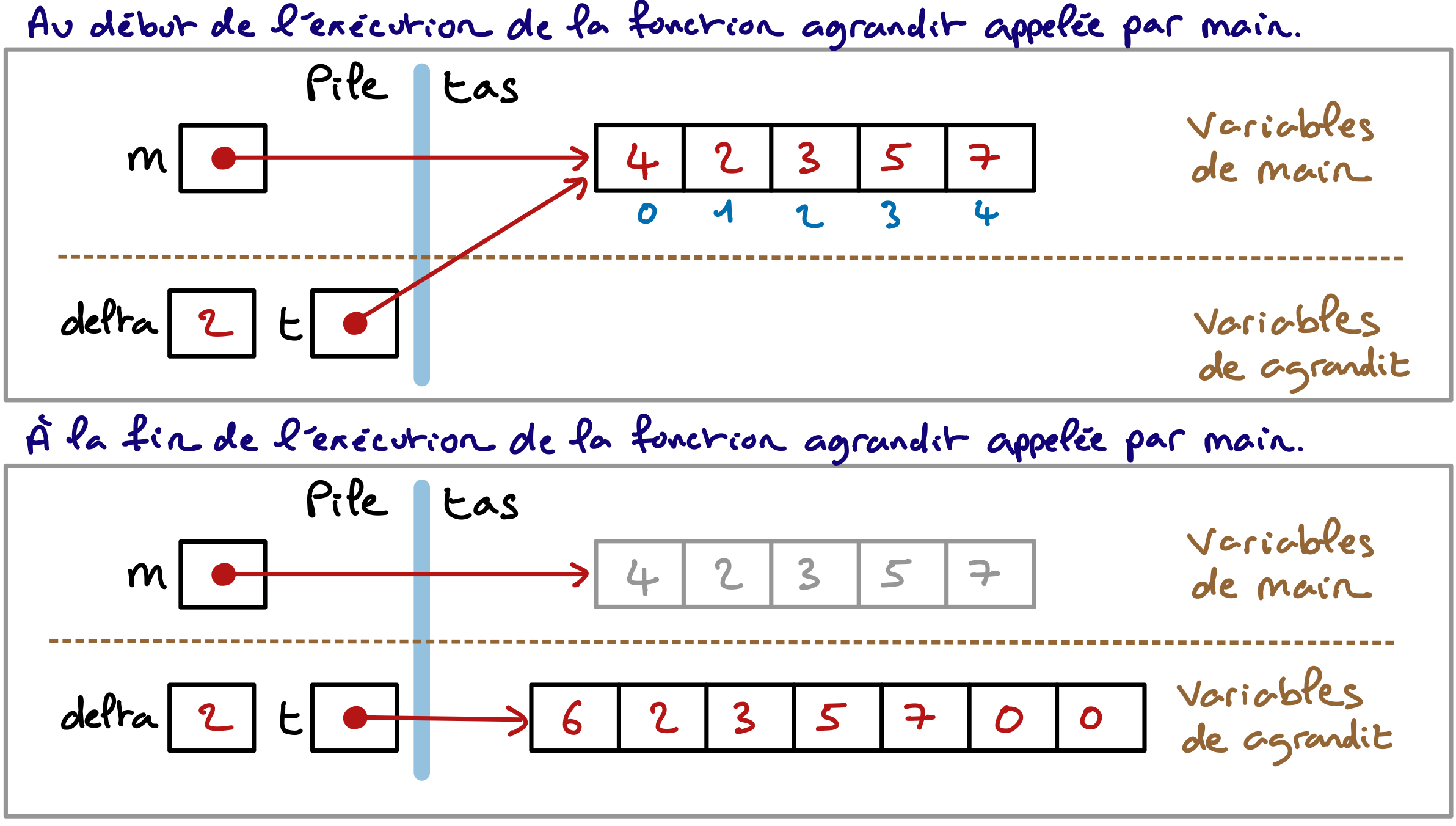
Si vous avez bien compris pourquoi c’est l’adresse d’une variable pointant le tableau informé à agrandir qu’il faut passer en paramètre à la fonction agrandit, et non directement l’adresse du tableau, alors vous pouvez continuer l’exercice en proposant une définition de la fonction demandée. Prenez le temps de bien réfléchir à toutes les étapes nécessaires.

"Indice1"

void agrandit(tabinf* t, int delta)
{
 tabinf tab = *t;   // Ligne A
 int n = tab[0];    // Ligne B
 // À compléter
 *t = newtab;       // Ligne C
}

En ligne A, l’adresse d’implantation du tableau à agrandir, que nous appellerons ancien tableau, est récupérée et placée dans la variable tab.

En ligne B, on place dans la variable n la taille de l’ancien tableau.

En ligne C, on place dans la variable pointée par t, c’est à dire la variable qui pointe initialement l’ancien tableau, l’adresse du nouveau tableau.

Voici la situation en mémoire après l’exécution de la ligne B, en supposant que la variable m, dans la fonction main, désigne le tableau à agrandir et que ce tableau, de taille 4, contient les valeurs 2, 3, 5 et 7.

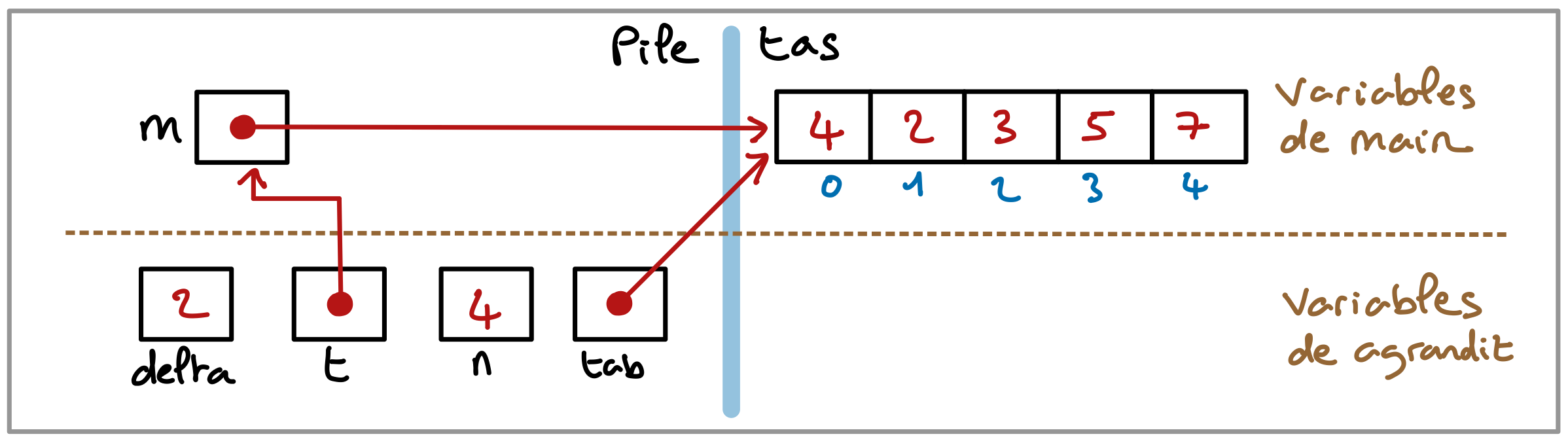
Entre les ligne B et C, il faut :

Créer le nouveau tableau en utilisant calloc.
Recopier les n valeurs de l’ancien tableau dans le nouveau.
Placer la valeur appropriée dans la première cellule du nouveau tableau.
Détruire l’ancien tableau.

"Solution"

void agrandit(tabinf* t, int delta)
{
 tabinf tab = *t;
 int n = tab[0];
 tabinf newtab = (tabinf)calloc(n+delta+1, sizeof(int));
 for(int i=1; i<=n; i++) newtab[i] = tab[i];
 newtab[0] = n+delta;
 free(tab);
 *t = newtab;
}

Proposez maintenant une variante de la fonction agrandit utilisant realloc au lieu de calloc. Attention, realloc, dans le cas d’un agrandissement, recopie les valeurs de l’ancien tableau dans le nouveau, mais n’initialise pas les valeurs suivantes du nouveau tableau.

"Solution"

void agrandit(tabinf* t, int delta)
{
 tabinf tab = *t;
 int n = tab[0];
 tab = (tabinf)realloc(tab, (n+delta+1)*sizeof(int));
 for(int i=n+1; i<=n+delta; i++) tab[i] = 0;
 tab[0] = n+delta;
 *t = tab;
}

Des variantes sont possibles. Chaque détail est important. Il est possible qu’une fonction se comporte apparemment correctement lors d’un test mais comporte néanmoins une erreur pouvant occasionner par exemple une fuite mémoire, ou placer des valeurs inopinées dans certaines cellules du nouveau tableau, mais pas à chaque fois. Un regard d’expert est nécessaire pour valider votre solution si elle est différente de celle-ci.

Contrôle continu 2 – M2 IIA

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

Variables : $A$ de domaine $\{1,2,3\}$, $B$ de domaine $\{4,5,6\}$, $D$ de domaine $\{7,8,9\}$, $C$ de domaine $\{10,11,12\}$.

Contraintes :

$q_1$ sur $A,B$ : $\{(1,4),(2,6),(3,5)\}$
$q_2$ sur $B,C$ : $\{(4,11),(5,10)\}$
$q_3$ sur $C,D$ : $\{(10,8),(11,9),(12,9)\}$
$q_4$ sur $A,D$ : $\{(1,9),(2,7),(3,9)\}$

Solution

Une solution : $A=1, B=4, C=11, D=9$.

A2 (1 point)

Donnez la représentation en extension de le contrainte logique $C = A \vee B$ (où, bien évidemment, les variables ont toutes le domaine $\{0,1\}$).

Solution

Sur $A,B,C$ : $\{(0,0,0),(0,1,1),(1,0,1),(1,1,1)\}$.

Partie B

Soit un entier positif $N$. Soit une variable $X$ ayant pour domaine $1..N$. Soit les variables Booléennes $X_1,…,X_N$ . On appelle représentation unaire d’une assignation $X=x$ l’assignation de $X_1,…,X_N$ telle que :

$X_x = 1$,
pour tout $y\in 1..N, y\neq x$, $X_y = 0$.

Par exemple, pour $N=3$, la représentation unaire de l’assignation $X=2$ est $X_1=0, X_2=1, X_3=0$.

Soit la variable $X$ de domaine $\{1,2,3\}$ et les variables $X_1, X_2, X_3$ de domaines $\{0,1\}$. On souhaite spécifier une ensemble $Q$ de contraintes appelées contraintes de liaison (chanelling constraints en anglais) qui assure que toute assignation de $X, X_1, X_2, X_3$ satisfait toutes les contraintes de $Q$ si et seulement si les valeurs de $X_1, X_2, X_3$ constituent la représentation unaire de la valeur de $X$.

B1 (1 point)

Donnez une spécification de $Q$ en extension. Une seule contrainte est suffisante, donc on a $Q=\{q\}$ où $q$ est une contrainte sur $X, X_1, X_2, X_3$.

Solution

$q$ sur $X,X_1,X_2,X_3$ : $\{(1,1,0,0),(2,0,1,0),(3,0,0,1)\}$

B2 (2 points)

Donnez une spécification de $Q$ en compréhension avec des contraintes arithmétiques. Une solution est possibles avec 2 contraintes.

Solution

$X_1 + X_2 + X_3 = 1$

$X1 + 2X_2 + 3X_3 = X$

B3 (1 point)

Donnez une spécification de $Q$ en compréhension dans le cas général d’une contrainte de liaison entre une variable $X$ et les variables Booléennes $X_1,…,X_N$, où $N$ est un entier positif quelconque.

Solution

$\sum_{i=1}^n X_i = 1$

$\sum_{i=1}^n i X_i = X$

Partie C

Pour chacune des questions, vous devez répondre en donnant, dans un ordre plausible, les valeurs retirées lors de la restauration de la cohérence de domaines du réseau de contraintes ou de la contrainte donnée dans l’énoncé. Aucune justification n’est demandée. Vous devez juste donner la liste des valeurs retirées en utilisant la notation $V\neq x$ pour dire que la valeur $x$ est retirée du domaine de $V$.

C1 (1 point)

Restaurez la cohérence de domaine de la contrainte $\text{alldiff}(A, B, C, D, E, F)$ dont les variables ayant respectivement pour domaines $\{1, 2, 4\}$, $\{1, 3, 5\}$, $\{2,3,6\}$, $\{4,5\}$, $\{4,6\}$, $\{5,6\}$.

Solution

$A \neq 4, B \neq 5, C \neq 6$ (dans n’importe quel ordre puisqu’il y a une seule contrainte)

C2 (1,5 point)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A, B, C$ ayant toutes pour domaine $\{1,2,3\}$.
Contraintes :
- $q_1$ : $A + 2B + 3C = 12$.
- $q_2$ : $A + 2B + 2C = 10$.

Solution

$q_2 : A\neq 1, A\neq 3$

$q_1 : B \neq 1, B \neq 3, C \neq 1, C \neq 3$

Il reste la valeur 2 dans chaque domaine, ce qui constitue une solution.

C3 (1,5 point)

Restaurez la cohérence de domaine du réseau suivant :

Variables : $A,B,C,D$ ayant toutes pour domaine $\{1,2,3\}$.

Contraintes :

$q_1$ sur $A,B$ : $\{(3,3),(2,1),(1,2)\}$
$q_2$ sur $B,C$ : $\{(3,3),(2,1),(1,1)\}$
$q_3$ sur $C,D$ : $\{(1,2),(2,1),(3,3)\}$
$q_4$ sur $A,D$ : $\{(1,1,(2,2),(3,3)\}$

Solution

$q_2 : C \neq 2$

$q_3 : D \neq 1$

$q_4 : A \neq 1$

$q_1 : B \neq 2$

Il reste respectivement dans les domaines de $A,b,C,D$ : $\{2,3\}, \{1,3\}, \{1,3\}, \{2,3\}$.

Partie D

D1 (2 points)

Soit le réseau de contraintes suivant dont les variables ont pour domaines {0,1} (représentant les valeurs vrai et faux) :

$(\neg a \vee b)$, $(\neg a \vee \neg b \vee c)$, $(\neg a \vee \neg b \vee \neg c)$, $(a \vee b \vee \neg e)$, $(e \vee a \vee d)$, $(e \vee a \vee \neg d)$, $(a \vee \neg b \vee e)$, $(\neg e \vee \neg b \vee d)$, $(\neg e \vee \neg b \vee \neg d)$.

Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Vous devez utiliser $a$ comme première variable de branchement. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.

Solution

CC2 – M2BDIA

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

Variables : $A, C$ de domaine $\{1,2,3\}$, $B,D$ de domaine $\{4,5,6\}$.

Contraintes :

Sur $A,B$ : $\{(1,5),(2,6),(3,4)\}$.
Sur $B,C$ : $\{(4,2),(5,3),(6,1)\}$.
Sur $C,D$ : $\{(1,5),(2,6),(3,4),(3,6)\}$.
Sur $A,D$ : $\{(1,6),(2,4),(3,5)\}$.

Solution

Une solution : $A=1, B=5, C=3, D=6$.

A2 (1 point)

Donnez la spécification en extension de la contrainte logique $A\vee \neg B \vee C$.

Solution

Sur $A,B,C$ : $\{(0,0,0),(0,0,1),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}$.

Partie B

Soit $V$ un ensemble de variables, $q$ une contrainte reliant les variables de $V$ et un ensemble $Q$ de contraintes tel que les variables reliées par chaque contrainte de $Q$ appartiennent à $V$.

On dit que $Q$ est équivalent à $q$ si et seulement si toute assignation complète des variables de $V$ satisfait toutes les contraintes de $Q$ si et seulement si elle satisfait $q$.

Par exemple, l’ensemble de contraintes $Q = \{A\neq B, A\neq C, B\neq C\}$ est équivalent à la contrainte $q = \text{allDiff}(A,B,C)$.

On appelle contrainte logique toute contrainte spécifiée en compréhension uniquement à l’aide des opérateurs $\vee, \wedge, \neg$.

Dans les questions suivantes, il sera uniquement question de variables Booléennes, donc à domaine $\{0,1\}$.

B1 (1 point)

Donnez un ensemble de contraintes logiques équivalent à la contrainte $X_1+…+X_N \neq 0$. Cet ensemble peut ne contenir qu’une seule contrainte.

Solution

$X_1\vee…\vee X_N$

B2 (1 point)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $A+B+C+D \leq 2$.

Solution

$(\neg A \vee \neg B \vee \neg C)$, $(\neg A \vee \neg B \vee \neg D)$, $(\neg A \vee \neg C \vee \neg D)$, $(\neg B \vee \neg C \vee \neg D)$

B3 (2 points)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $X_1+…+X_N \leq 1$, pour tout entier $N$ supérieur à 1.

Solution

$\forall i \in 1..N, \forall j \in i+1..N, (\neg X_i \vee \neg X_j)$

Partie C

Pour chacune des questions, vous devez répondre en donnant, dans un ordre plausible, les valeurs retirées lors de la restauration de la cohérence de domaines du réseau de contraintes ou de la contrainte donnée dans l’énoncé. Aucune justification n’est demandée. Vous devez juste donner, à raison d’une ligne par visite d’une contrainte, la liste des valeurs retirées en utilisant la notation $V\neq x$ pour dire que la valeur $x$ est retirée du domaine de $V$.

Par exemple pour décrire le filtrage du réseau $q_1 : A<B$, $q_2 : B<C$ où $A, B, C$ ont pour domaine $\{1,2,3\}$, vous devez adopter la présentation suivante :

$q_1$ : $A\neq 3, B\neq 1$
$q_2$ : $B\neq 3, C\neq 1, C\neq 2$
$q_1$ : $A\neq 2$

C1 (2points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A$ de domaine $\{1,2,3\}$, $B$ de domaine $\{4,5,6\}$, $C$ de domaine $\{7,8,9\}$.

Contraintes :

$q_1$ sur $A,B$ : $\{(1,5),(2,4),(3,6)\}$
$q_2$ sur $B,C$ : $\{(4,8),(5,7),(6,8)\}$
$q_3$ sur $A,C$ : $\{(1,7),(2,8),(3,9)\}$

Solution

$q_2 : C\neq 9$
$q_3 : A\neq 3$
$q_1 : B \neq 6$

C2 (2 points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A,B,C$ de domaine $\{1,2,3\}$.

Contraintes :

$q_1$ : $A+B+C=6$
$q_2$ : $A+2B+C=9$
$q_3$ : $2A+B+3C=10$

Solution

$q_2 : B\neq 1$
$q_3 : A\neq 3, C\neq 3$
$q_1 : A\neq 1$
$q_2 : B\neq 2, C \neq 2$

Partie D

D1 (2 points)

Soit le réseau de contraintes suivant :

Variables : $A,B,C,D$ ayant toutes pour domaine $\{3,7,11\}$.

Contraintes :

$A+B+C+D \leq 17$
$A+B+C+D \geq 17$

Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.

Solution

Contrôle continu 1 – M2 IIA

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

"Solution"

Aucune solution.

A2 (1 point)

Soient les variables A, B, C de domaines respectifs {1,2}, {2,3} et {3,4}. Soient les contraintes suivantes :

q1 sur A, B : {(1,2), (2,3)}.
q2 sur B, C : {(2,4)}.
q : q1 ou q2 (la contrainte satisfaite par et seulement par les assignations de A, B, C qui satisfont q1 ou q2).

Donnez la représentation en extension de q.

"Solution"

Sur $A,B,C$ : $\{(1,2,3),(1,2,4),(2,3,3),(2,3,4),(2,2,4)\}$.

Partie B

B1 (1 point)

On veut placer $k$ personnes sur un coté d’une table rectangulaire disposant de $k$ places. On attribue, par commodité, un numéro compris entre $1$ et $k$ à chaque place et on fait de même pour chaque personne à placer.

Chaque personne $i$ peut exclure certaines autres personnes, c’est à dire refuser que ces autres personnes (si applicable) soient placées à coté de lui. Les personnes exclues par une personne $x$ sont données par un ensemble $E_x$. Voici un exemple avec $k=4$ :

\[E_1=\{2,3\}, E_2=\{1\}, E_3=\{1,4\}, E_4=\{3\}
\]

La personne 1 exclut les personnes 2 et 3,
la personne 2 exclut la personne 1,
la personne 3 exclut les personnes 1 et 4,
la personne 4 exclut la personne 3.

Voici une solution permettant de placer les 4 personnes en respectent leurs incompatibilités.

Proposez une modélisation en extension de l’exemple ci-dessus en utilisant les variables, domaines et contraintes qui vous paraissent les plus pertinentes.

"Solution"

Une variable par place : $P_1, P_2, P_3, P_4$ de domaine $\{1,2,3,4\}$. $P_i=j$ signifie que la personne $j$ occupe la place $i$.

Contraintes de compatibilité :

Sur $P_1, P_2$ : $\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}$.
Sur $P_2, P_3$ : $\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}$.
Sur $P_3, P_4$ : $\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}$.

Contraintes de différence (pour que chaque place soit occupée par une personne différente) :

Sur $P_1, P_3$ : $\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}$.
Sur $P_1, P_4$ : $\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}$.
Sur $P_2, P_4$ : $\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}$.

B2 (3 points)

On revient au cas général où on a $k$ personnes à placer. On souhaite modéliser le problème à l’aide de variables Booléennes $P_{ix}$, pour $i$ et $x$ compris entre 1 et $k$, avec la convention suivante : $P_{ix}=1$ signifie que la place $i$ est occupée par la personne $x$.

Donnez une spécification en compréhension de toutes les contraintes nécessaires, les données du problèmes étant les ensembles $E_1$ à $E_k$. Vous pouvez utiliser des contraintes arithmétiques et / ou logiques.

"Solution"

Chaque place est occupée par une personne, chaque personne occupe exactement une place :

$\forall i \in 1..k, \sum_{x=1}^k P_{i,x} = 1$, $\forall x \in 1..k, \sum_{i=1}^k P_{i,x} = 1$.

Incompatibilités :

$\forall i\in 1..k-1, \forall x\in 1..k, \forall y\in E_x, \neg(P_{i,x}\wedge P_{i+1,y})$

$\forall i\in 1..k-1, \forall x\in 1..k, \forall y\in E_x, \neg(P_{i+1,x}\wedge P_{i,y})$

Partie C

C1 (1 point)

Restaurez la cohérence de domaine de la contrainte $\text{alldiff}(A, B, C, D, E)$ dont les variables ont les domaines suivants :

$A, B$ : $\{1, 2, 3\}$, $C$ : $\{1, 2, 3, 4\}$, $D$ : $\{4,2\}$, $E$ : $\{4,3\}$.

"Solution"

$D\neq 4$, $A\neq 2$, $B\neq 2$, $C\neq 2$, $E\neq 4$, $E\neq 3$, incohérence globale.

C2 (2 points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A$ de domaine $\{1,2\}$, $B$ de domaine $\{4,5\}$, $C$ de domaine $\{4,5\}$, $X$ de domaine $\{1,2,3\}$, $Y$ de domaine $\{1,2,3\}$.
Contraintes :
- Sur $A, B, C$ : $\{(1,4,5), (1,5,4), (2,5,5)\}$.
- Sur $B, X$ : $\{(4,1), (4,2), (5,3)\}$.
- Sur $C, Y$ : $\{(4,3), (5,2)\}$.
- Sur $X,Y$ : $\{(1,2), (2,3), (3,1)\}$.

"Solution"

$Y\neq 1, X\neq 3, B\neq 5, A\neq 2, C\neq 4, Y\neq 3, X\neq 2$

Le filtrage peut être plus facile en s’appuyant sur une représentation graphique telle que celles-ci :

C3 (1 point)

Restaurez la cohérence de domaine de la contrainte $9 X_2 + 3 X_1 + X_0 = Y$ dont les variables ont les domaines suivants :

$X_0, X_1, X_2$ : $\{0,1,2\}$, $Y$ : $\{10,13,16\}$.

"Solution"

$X_2\neq 0, X_2\neq 2, X_0\neq 0, X_0 \neq 2$

Partie D

D1 (2 points)

Soit le réseau de contraintes suivant dont les variables ont pour domaines {0,1} (représentant les valeurs vrai et faux) :

$(a \vee \neg b), (a \vee c), (b \vee \neg c), (\neg a \vee c), (\neg c \vee \neg d), (\neg a \vee \neg b \vee \neg c \vee d \vee e)$.

Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Choisissez les variables de branchement qui vous paraissent être pertinentes pour minimiser l’arbre de recherche. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.

"Solution"

Contrôle continu 1 – M2 BDIA

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

A2 (1 point)

"Solution"

Une solution : $A=1, B=4, C=8, D=10$.

Soient les variables A, B, C de domaines respectifs {1,2}, {2,3} et {3,4}. Soient les contraintes suivantes :

q1 : A < B.
q2 : B < C.
q : q1 et q2 (la contrainte satisfaite par et seulement par les assignations de A, B, C qui satisfont q1 et q2).

Donnez les représentations en extension de q1, q2 et q.

"Solution"

$q_1$ : sur $A,B$, $\{(1,2),(1,3),(2,3)\}$.
$q_2$ : sur $B,C$, $\{(2,3),(2,4),(3,4)\}$.
$q$ : sur $A,B,C$, $\{(1,2,3),(1,2,4),(1,3,4),(2,3,4)\}$.

Partie B

Soit $N$ un entier au mois égal à 3 et $A_1,…,A_N$, $B_1,…,B_N$ des variables Booléennes, i.e., ayant pour domaine $\{0,1\}$.

Toute assignation complète des variables $A_1,…,A_N$ représentent le positionnement d’une tâche $A$ dont l’heure de début est la plus petite valeur $i$ telle que $A_i=1$ et la durée est le nombre de valeurs de consécutives assignées à 1.

Par exemple, pour $N=5$ les valeurs autorisées des variables $A_1$ à $A_5$ pour représenter de tâche d’une durée de 3 heures sont les suivantes :

11100 // tâche A commence à 0h, durée 3h
01110 // tâche A commence à 1h, durée 3h
00111 // tâche A commence à 2h, durée 3h

Les assignations dans lesquelles un ou plusieurs 0 sont encadrés par des 1, telles que 10110, sont interdites.

La même convention est appliquée aux variables $B_1,…,B_N$ pour la représentation d’une tâche $B$.

Pour exprimer mathématiquement que tous les bits à 1 d’une assignation sont consécutifs, on dit qu’il ne peut y avoir de motif 1…01 ni de motif 10…1 dans la séquence.

Ceci correspond aux deux ensembles de contraintes suivants :

$\forall i\in 2..N-1, \forall j\in 1..i-1, \neg A_j \vee A_i \vee \neg A_{i+1}$
$\forall i\in 1..N-2, \forall j\in i+2..N, \neg A_i \vee A_{i+1} \vee \neg A_{j}$

Par exemple, l’assignation 10110 falsifie la contrainte $\neg A_1 \vee A_3 \vee \neg A_4$ qui est une des contraintes mentionnées plus haut.

Les mêmes contraintes sont appliquées aux variables $B_1,…,B_N$.

B1 (1 point)

Soient $K_A$ et $K_B$ deux entiers. On suppose que $K_A+K_B\leq N$. Donnez une spécification en compréhension (sur les variables $A_1,…,A_N$, $B_1,…,B_N$) des contraintes qui expriment les propriétés suivantes :

La durée de la tâche $A$ est $K_A$,
La durée de la tâche $B$ est $K_B$.

"Solution"

$\sum_{i=1}^N A_i = K_A$.
$\sum_{i=1}^N B_i = K_B$.

B2 (1 point)

Donnez une spécification en extension de la contrainte qui exprime que la tâche $A$ dure 2 heures, pour $N=5$.

"Solution"

Sur $A_1,A_2,A_3, A_4,A_5$ : $\{(1,1,0,0,0),(0,1,1,0,0),(0,0,1,1,0),(0,0,0,1,1)\}$.

B3 (2 points)

Donnez la spécification en compréhension les contraintes supplémentaires (sur les variables $A_1,…,A_N$, $B_1,…,B_N$) qui permettent de dire que la tâche $A$ doit être complètement réalisée lorsque la tâche $B$ commence.

Vous devez utiliser des contraintes logiques (basées sur $\neg, \vee, \wedge$) ou arithmétiques linéaires (basées sur -, +, <, >, =, etc.) ou des compositions logiques de contraintes arithmétiques.

Voici un exemple d’assignations avec $N=10$ et $K=3$ qui satisfont les contraintes supplémentaires que vous devez spécifier.

0011100000 // tâche A
0000001110 // tâche B

Et trois exemples qui doivent falsifier au moins une de ces contraintes.

0011110000 // tâche A
0000111100 // tâche B

0011100000 // tâche A
0111000000 // tâche B

0000011000 // tâche A
0110000000 // tâche B

"Solution"

$\forall i \in 1..N$, $\forall j\in 1..i$, $\neg(A_i \wedge B_j)$.

D’autres solutions existent.

Partie C

C1 (4 points)

Voici le réseau de contrainte qui modélise le problème de l’existence d’une règle de Golomb de longueur 6 à 4 graduations.

Variables :

$G_0$ de domaine $\{0\}$, $G_3$ de domaine $\{6\}$,
$G_1, G_2$ de domaine $\{1,2,3,4,5\}$
$D_0, D_1, D_2, D_3, D_4, D_5$ de domaine $\{1,2,3,4,5,6\}$.

Contraintes :

$G_0 < G_1, G_1 < G_2, G_2 < G_3$,
$D_0=G_1-G_0$, $D_1=G_2-G_0$, $D_2=G_3-G_0$, $D_3=G_2-G_1$, $D_4=G_3-G_1$, $D_5=G_3-G_2$,
AllDiff$(D_0, D_1, D_2, D_3, D_4, D_5)$

Voici une représentation graphique de ce réseau de contraintes :

Restaurez la cohérence de domaine de ce réseau de contrainte. Donnez les valeurs retirées dans un ordre cohérent avec le principe de filtrage. Utilisez la notation $V\neq x$ pour indiquer que la valeur $x$ est retirée du domaine de la variable $V$.

Par exemple, vous pouvez commencer par $D_2 \neq 1$ car la valeur $D_2=1$ n’a pas de support pour la contrainte $D_2=G_3-G_0$. Mais il existe plusieurs séquences correctes.

"Solution"

$G_1\neq 5, G_2\neq 1, D_0\neq 5, D_0\neq 6, D_3\neq 5, D_3\neq 6,$

$D_5\neq 5, D_5\neq 6, D_1\neq 1, D_1\neq 6, D_4\neq 1, D_4\neq 6,$

$D_2\neq 1, D_2\neq 2, D_2\neq 3, D_2\neq 4, D_2\neq 5.$

Partie D

D1 (2 points)

Voici un réseau de 6 contraintes logiques et le début de l’arbre de recherche de l’algorithme MAC sur ce réseau. Vous devez compléter l’arbre en choisissant au mieux (si applicable) les variables de branchement restantes. A chaque nœud ou feuille, redonnez les domaines en barrant les valeurs éliminées par filtrage ou par assignation de la variable de branchement. A chaque feuille de l’arbre de recherche, précisez s’il y a échec ou solution.

"Solution"

POO – CC2 avec corrigés

Partie A

A1 (2 points)

On rappelle que l’exécution des lignes de code suivantes…

String s = "aaa";
s = s + 'b';
System.out.println(s);

… a pour effet l’affichage :

aaab

Donner le code d’une méthode de classe rep qui accepte en paramètre un caractère c et un entier n, et qui retourne la chaîne constituée de n occurrences de c. Par exemple, l’appel…

System.out.println(rep('x', 5));

…devra avoir pour effet l’affichage :

xxxxx

"Solution"

public static String rep(char c, int n)
{
    String r = "";
    for(int i=0; i<n; i++)
    {
        r = r + c;
    }
    return r;
}

A2 (1 point)

Donnez les lignes de code permettant d’obtenir la configuration suivante en mémoire, en utilisant la méthode rep de la question précédente. Vous pouvez répondre même si vous n’avez pas traité la question précédente ou si votre réponse est incorrecte. Le correcteur considérera que la méthode rep fonctionne comme attendu.

"Solution"

String t = rep('a',3);
String u = t;

Partie B

On considère la classe Terrain suivante :

public class Terrain
{
    private String nom;
    private double x1; private double y1;
    private double x2; private double y2;

    public Terrain(String nom, double x1, double y1, double x2, double y2)
    {
        this.nom = nom;
        this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2;
    }
  
    public Terrain clone()
    {
        return new Terrain(nom, x1, y1, x2, y2);
    }

    public double surface()
    {
        return (x2-x1) * (y2-y1);
    }

    public String toString()

    {
        return "Terrain : " + nom + "(" + x1 + "," + y1 + ") (" + x2 + "," + y2 +")";
    }
}

Qui représente un terrain (par exemple agricole) délimité par des coordonnées géographiques exprimées en mètres dans une repère local quelconque.

La classe suivante représente un cadastre regroupant une collection de terrains.

public class Cadastre 
{
    private ArrayList<Terrain> terrains;

    public Cadastre()
    {
        this.terrains = new ArrayList<>();
    }

    public void add(double x1, double y1, double x2, double y2, String nom)
    {
        terrains.add(new Terrain(nom, x1, y1, x2, y2));
    }

    public double surface()
    {
        double r = 0.0;
        for(Terrain t : terrains)
        {
            r = r + t.surface();
        }
        return r;
    }
}

B1 (1 point)

Ajoutez à la classe Terrain une méthode renomme permettant de changer le nom du terrain courant. Le nouveau nom devra être passé en paramètre.

"Solution"

public void renomme(String nouveauNom)
{
    this.nom =nouveauNom;
}

B2 (2 points)

Réalisez un constructeur en copie pour la classe Cadastre. Ce constructeur doit permettre de créer une instances de Cadastre identique à celle désignée en argument, mais ne pouvant donner lieu à aucun effet de bord ultérieur : toute modification du cadastre original ne devra avoir aucun effet sur la copie, et réciproquement.

"Solution"

public Cadastre(Cadastre model)
{
    this();
    for(Terrain t : model.terrains)
    {
        terrains.add(t.clone());
    }
}

B3 (1 point)

Avec les constructeurs et méthodes disponibles dans les classes Terrain et Cadastre, (en supposant que le constructeur en copie soit correctement programmé – vous pouvez donc répondre à cette question même si vous n’avez pas répondu à la précédente, ou si votre réponse est incorrecte) est-il possible d’obtenir la configuration suivante en mémoire ?

Si oui, donnez les lignes de code permettant d’obtenir cette configuration. Si non, expliquez pourquoi.

"Solution"

Non, c’est impossible car le seul moyen d’ajouter un terrain à un cadastre est d’utiliser la méthode add qui crée une copie du terrain à ajouter. On ne peut donc avoir deux instances de Cadastre contenant une référence d’une même instance de Terrain.

Partie C

Soit la classe suivante, qui représente (partiellement, par souci de concision et simplicité) un véhicule à moteur thermique.

public abstract class VehiculeThermique
{
    private double qteCarburant; // Quantité de carburant dans le réservoir
    private int charge;          // Charge actuelle en Kg
    private String nom;          // Nom du véhicule

    public VehiculeThermique(String nom)
    {
        this.nom = nom;
        this.charge = 0;
        this.qteCarburant = 0.0;
    }

    public int getCharge() { return charge;}
    public double getQteCarburant() { return qteCarburant;}
    public void setCharge(int poids) {charge = poids;}
  
    public void remplir(double qte)
    {
        qteCarburant = qteCarburant + qte;
    }

    public abstract double consommation();

    public double autonomie()
    {
        // À compléter
    }

    public String toString()
    {
        return "Véhicule consommant " + consommation() + "l / 100Km";
    }
}

La méthode consommation retourne la consommation du véhicule courant exprimée en litres par 100Kms.

La méthode autonomie retourne le nombre de kilomètres restant à parcourir avec la quantité de carburant actuellement dans le réservoir (valeur de l’attribut qteCarburant). Pour mémoire, avec $q$ litres de carburant et une consommation de $c$ litres au 100 Kms, on peut parcourir $100 \: q/c$ Kms.

Soit la classe suivante, qui représente un modèle particulier de véhicule à moteur thermique appelé Fourgon à essence.

public class FourgonEssence extends VehiculeThermique
{
    private double indiceOctane;

    public FourgonEssence(String nom, double ioct)
    {
        // À compléter
    }

    public String getTypeCarburant() { return "Essence";}

    public String toString()
    {
        // À compléter
    }
}

C1 (2 points)

Donnez le code de la méthode autonomie de la classe VehiculeThermique et le code à ajouter à la classe FourgonEssence pour que la méthode autonomie fonctionne correctement, sachant qu’un fourgon à essence consomme, pour parcourir 100 Kms, 5 litres d’essence plus 0.02 litre par Kg de charge.

"Solution"

public double autonomie()
{
    return 100 * (getQteCarburant() / consommation());
}

public double consommation()
{
    return 5.0 + (0.02*getCharge());
}

C2 (1 point)

Donnez le code du constructeur de la classe FourgonEssence. Le deuxième paramètre est l’indice d’octane du carburant utilisable.

"Solution"

public FourgonEssence(String nom, double ioct)
{
    super(nom);
    this.indiceOctane = ioct;
}

C3 (1 point)

La classe FourgonEssence contient une méthode…

    public String getTypeCarburant() 
    { 
        return "Essence indice octane " + indiceOctane;
    }

…qui retourne le type de carburant utilisé.

Comment faire pour imposer à toute classe concrète dérivée de VehiculeThermique d’avoir une méthode ayant pour signature…

public String getTypeCarburant()

… en utilisant une interface ?

Précisez ce qu’il faut mettre dans l’interface et quel modification il faut apporter à la définition de la classe VehiculeThermique.

"Solution"

public interface Thermique
{
    String getTypeCarburant();
}

C4 (1 point)

Réalisez une méthode toString pour la classe FourgonEssence. Cette méthode doit appeler la méthode toString de la classe VehiculeThermique et utiliser sa valeur de retour. L’exécution des lignes de code suivantes…

VehiculeThermique v1 = new FourgonEssence("Fourgon d'Olivier", 0.98);
v1.setCharge(150);
System.out.println(v1);

…doit avoir pour effet l’affichage :

Fourgon à essence : Véhicule consommant 8.0l / 100Km

"Solution"

public String toString()
{
    return "Fourgon à essence : " + super.toString();
}

Partie D

La classe suivante représente un tableau évolué d’entiers dans lequel certaines cases peuvent être vides (ce qui est interdit dans un tableau d’entiers classique dans lequel toute case à une valeur). Attention, cette classe est un un prototype non finalisé qui n’a pas encore les comportements souhaités.

public class SuperTabInt
{
    private int[] data;
    private boolean[] flag;

    public SuperTabInt(int size)
    {
        this.data = new int[size];
        this.flag = new boolean[size];
    }

    public void write(int i, int val)
    {
        data[i] = val; flag[i] = true;
    }

    public int read(int i)
    {
        return data[i];
    }

    public String toString()
    {
        String r = "[ ";
        for(int i=0; i<data.length; i++)
        {
            if(flag[i]) r += data[i] + " ";
            else r += "# ";
        }
        return r + "]";
    }
}

Le principe de représentation est le suivant :

Soit une instance de SuperTabInt représentant un tableau évolué. Soit i un indice valide dans ce tableau évolué. Si la cellule d’indice i du tableau évolué est vide, alors flag[i] vaut false, sinon flag[i] vaut true. Dans le cas où la cellule d’indice i n’est pas vide, sa valeur est dans data[i].

Mais on ne peut évidemment pas utiliser les crochets pour accéder à une cellule d’un tableau évolué représenté par une instance de SuperTab. cette écriture avec crochets est réservée aux tableaux ordinaires. Pour modifier ou lire une cellule de tableau évolué, on doit utiliser les méthodes read et write .

Voici un exemple qui commence par la création d’un tableau évolué de 10 cellules…

SuperTabInt tab = new SuperTabInt(10);
tab.write(2, 55);
tab.write(3, 56);
System.out.println(tab.read(3));
System.out.println(tab); // Appel de toString

…qui produit les affichages suivants :

56
[ # # 55 56 # # # # # # ]

Mais en l’état, cette classe ne donne pas satisfaction. On souhaite qu’une exception de type BadAccess soit levée lors de certaines situations :

Tentative de lecture ou écriture à un indice négatif.
Tentative de lecture ou écriture à un indice au delà de la dernière cellule accessible.
Tentative de lecture d’une cellule vide. (Une cellule est vide tant qu’aucune valeur n’y a été écrite par la méthode write).

La classe d’exception BadAccess est définie de la manière suivante.

public class BadAccess extends Exception
{
    private int code;  // Code d'erreur
    private int index; // indice auquel l'erreur s'est produite

    public BadAccess(int code, int index)
    {
        this.code = code;
        this.index = index;
    }

    public String toString()
    {
        String msg;
        if(code==1) msg = "Negative index";
        else if(code==2) msg = "Index too large";
        else msg = "Attempt to read an empty cell";
      
        return "SuperTab error : " + msg + " at index " + index;
    }
}

Lors de la création d’une instance d’exception de cette classe, on indique un code (1, 2 ou 3) qui renseigne le type d’erreur et l’indice auquel l’erreur s’est produite.

D1 (2 points)

Réalisez des nouvelles versions des méthodes write et read de la classe SuperTabInt qui lèvent une exception de type BadAccess dans les situation décrites ci-dessus (avec les codes et indices d’erreur appropriés).

"Solution"

public void write(int i, int val) throws BadAccess
{
    if(i<0) throw new BadAccess(1, i);
    else if(i>=data.length) throw new BadAccess(2, i);
    data[i] = val; flag[i] = true;
}

public int read(int i) throws BadAccess
{
    if(i<0) throw new BadAccess(1, i);
    else if(i>=data.length) throw new BadAccess(2, i);
    else if(!flag[i]) throw new BadAccess(3, i);
    return data[i];
}

D2 (2 points)

Donnez le code complet d’une méthode main qui réalise les actions suivantes :

Création d’une instance de SuperTabInt représentant un tableau évolué de 10 entiers.
Écriture des valeurs 55, 56 et 33 aux indices 2, 3 et 5, respectivement.
Affichage de la valeur située à l’indice 4 (comme cette case est vide, une exception sera levée par la méthode read).

Dans le cas où une exception est levée, deux actions doivent être réalisées :

Affichage du tableau évolué à l’aide de la méthode toString de la classe SuperTabInt.
Affichage de la chaîne produite par la méthode toString de la classe BadAccess.

En l’occurrence, avec les actions demandées, l’affichage produit serait :

[ # # 55 56 # 33 # # # # ]
SuperTab error : Attempt to read an empty cell at index 4

Mais ce message pourrait être différent pour des variantes du programme (non demandées) qui tenteraient une lecture ou écriture à un indice incorrect.

"Solution"

public static void main(String[] args)
{
    SuperTabInt tab = new SuperTabInt(10);

    try
    {
        tab.write(2, 55);
        tab.write(3, 56);
        tab.write(5, 33);
        System.out.println(tab.read(4));
    }
    catch(BadAccess e)
    {
        System.out.println("Tableau : " + tab);
        System.out.println(e);
    }
}

Partie E

Soit la méthode de classe suivante…

public static boolean sorted(List<Double> w)
{
    for(int i=0; i<w.size()-1; i++)
    {
        if(w.get(i) > w.get(i+1)) return false;
    }
    return true;
}

… qui permet de vérifier si une liste de valeurs de type Double est triée par ordre croissant (i.e. chaque valeur est au moins égale à la précédente, si applicable).

E1(1 point)

Donnez un exemple de liste de 10 valeurs qui maximise le temps d’exécution de la méthode, et d’une liste de 10 valeurs qui minimise ce temps d’exécution.

"Solution"

Donnée facile :    2.0, 1.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0
Donnée difficile : 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0

E2 (2 points)

Soit la méthode main suivante :

public static void main(String[] args)
{
    List data = new ArrayList<Double>();
		
    // Code produisant dans data une liste de 100000 valeurs
    // qui maximise le temps d'exécution de la méthode sorted
  
    System.out.println("Liste remplie");
    System.out.println(sorted(data));
}

On exécute le programme et on constate l’affichage immédiat suivant :

Liste remplie
true

La deuxième ligne semble s’afficher sans délai après la première. En pratique, il y a un délai qui inclut le temps d’exécution de la méthode sorted, mais qui est trop court pour être perceptible par un observateur humain.

On refait l’expérience en remplaçant la première ligne de code de main par la ligne suivante :

   List data = new LinkedList<Double>();

On observe le même comportement, mais il s’écoule une dizaine de secondes entre l’affichage de Liste remplie et l’affichage de true. Expliquez pourquoi. Précisez les complexités en temps dans le pire des cas de la méthode sorted avec chacune des deux structures de données ArrayList et LinkedList.

"Solution"

Avec ArrayList, l’accès à un élément situé à une position $i$ arbitraire se fait en temps constant. La complexité de la méthode sorted est donc linéaire. Avec LinkedList, l’accès à un une position $i$ arbitraire se fait en temps linéaire. La complexité de la méthode sorted est donc quadratique.

E3 (1 point)

Réalisez une méthode sortedOpt qui fait exactement la même chose que la méthode sorted mais en ayant le même ordre de complexité en temps dans le pire des cas pour une liste de type ArrayList et pour une liste de type LinkedList.

"Solution"

En utilisant un itérateur, on peut parcourir la liste en temps linéaire tout en comparant les éléments successifs.

public static boolean sortedOpt(List<Double> w)
{
    double current = w.get(0);
    for(double x : w)
    {
        if(x < current) return false;
        current = x;
    }
    return true;
}

POO – CC1 avec corrigés

Partie A

A1 (2 point)

Réalisez une méthode de classe…

public static void amplitude(int[] tab)
{
  // À compléter
}

…qui retourne la différence entre la plus grande et la plus petite valeur du tableau tab. Par exemple si tab contient les valeurs 5, 1, 4, 23, 4 ,4, 8, 5, alors la valeur de retour devra être 22 c’est à dire 23-1.

"Solution"

public static int amplitude(int[] tab)
{
    int mini = tab[0]; int maxi = tab[0];
    for(int i=1; i<tab.length; i++)
    {
        if(tab[i] > maxi) maxi = tab[i];
        else if(tab[i] < mini) mini = tab[i];
    }
    return  maxi - mini;
}

A2 (1 point)

Réalisez une méthode main qui crée un tableau d’entier contenant les valeurs de l’exemple précédent, qui appelle la méthode amplitude avec ce tableau et affiche le résultat.

"Solution"

public static void main(String[] args)
{
    int[] tab = {5, 1, 4, 23, 4, 4, 8, 5};
    System.out.println(amplitude(tab));
}

Partie B

Soit une classe Terrain représentant un terrain agricole de forme rectangulaire localisé par les coordonnées géographiques (qui sont des valeurs de types double, en mètres) de deux de ses coins opposés. A cette fin, la classe Terrain a 4 attributs privés de type double nommés x1, y1, x2, y2. Elle possède en outre un attribut privé nom de type String qui permet d’attribuer un nom à chaque terrain.

La classe Terrain dispose d’un constructeur Terrain(double x1, double y1, double x2, double y2, String nom) permettant la création d’une instance à l’aide des informations fournies en paramètres. Elle dispose également d’une méthode toString retournant une description textuelle du terrain courant. On supposera que x1 < x2 et y1 < y2.

public class Terrain
{
    private String nom;
    private double x1; private double y1;
    private double x2; private double y2;

    public Terrain(String nom, double x1, double y1, double x2, double y2)
    {
        this.nom = nom;
        this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2;
    }

    public String toString()

    {
        return "Terrain : " + nom + "(" + x1 + "," + y1 + ") (" + x2 + "," + y2 +")";
    }
}

Soit une classe Cadastre représentant une liste de plusieurs terrains. Nous appellerons cadastre toute instance de cette classe. Cette classe a un attribut privé terrains de type ArrayList<Terrain> qui permet le stockage de toutes les instances de Terrain du cadastre courant.

B1 (1 point)

Donnez la définition du constructeur de la classe Cadastre.

"Solution"

public Cadastre()
{
    this.terrains = new ArrayList<>();
}

B2 (1 point)

Donnez la définition d’une méthode d’instance public void add(double x1, double y1, double x2, double y2, String nom) de la classe Cadastre qui ajoute un nouveau terrain à la liste.

"Solution"

public void add(double x1, double y1, double x2, double y2, String nom)
{
    terrains.add(new Terrain(nom, x1, y1, x2, y2));
}

B3 (1 point)

On suppose que la classe Terrain a une méthode d’instance public double surface() qui retourne la surface du terrain courant.

Donnez la définition d’une méthode d’instance public double surface() de la classe Cadastre qui retourne la somme des surfaces des terrains du cadastre courant.

"Solution"

public double surface()
{
    double r = 0.0;
    for(Terrain t : terrains)
    {
        r = r + t.surface();
    }
    return r;
}

B4 (1point)

Donnez les lignes de codes, supposées être dans une méthode de classe void test() située dans une classe Test, permettant de créer un cadastre, d’y ajouter deux terrains, et d’afficher la surface cumulée des terrains du cadastre.

"Solution"

Cadastre cad = new Cadastre();
cad.add(100,200,120,230,"parcelle 1");
cad.add(560,320,570,330,"parcelle 2");
System.out.println(cad.surface());

Partie C

On considère les classes et interface suivantes.

La classe Point représente juste un point avec deux coordonnées de type double.

public class Point
{
    private double x,y;

    public Point(double x, double y) { ... }

    public String toString() { ... }
}

La classe Courbe représente une liste de points pouvant être interprétée comme une courbe si on imagine que chaque point est relié au suivant (si applicable).

public class Courbe
{
    private ArrayList<Point> points;

    public Courbe(){ ... }

    public void add(double x, double y) { ... }

    public String toString() { return }
}

Voici une représentation graphique de l’instance de courbe représentée par la liste de points [(1.0,1.0), (2.0,3.0), (3.0,2.0)].

Ceci est juste donné à titre d’exemple. La partie affichage graphique n’est pas du tout traitée dans cet exercice.

L’interface Graphable oblige les classes qui l’implémentent à être dotées d’une méthode permettant de produire une instance de courbe représentée par une liste de n points dont les abscisses (coordonnées $x$) vont de min à max avec des écarts constants entre ces abscisses.

Par exemple si n vaut 5, min vaut 10.0 et max vaut 12.0, les abscisses des 5 points devront être 10.0, 10.5, 11.0, 11.5 et 12.0.

public interface Graphable
{
    public Courbe getCourbe(double min, double max, int n);
}

La classe abstraite Fonction représente une fonction calculable. Elle dispose d’une méthode abstraite getImage qui accepte en paramètre une valeur x et retourne l’image de x par cette fonction. Par exemple, dans une classe dérivée de Fonction qui représente la fonction $x \mapsto x^2$, l’appel getImage(3.0) retournera 9.0.

public abstract class Fonction implements Graphable
{
    public abstract double getImage(double x);

    public Courbe getCourbe(double min, double max, int n)
    {
        // À compléter
    }
}

C1 (2 points)

Implémentez la méthode getCourbe de la classe Foncton.

"Solution"

public Courbe getCourbe(double min, double max, int n)
{
    double delta = (max - min) / (n - 1);
    double x = min;
    Courbe r = new Courbe();
    for(int i = 0; i< n; i++)
    {
        r.add(x, getImage(x));
        x = x + delta;
    }
    return r;
}

C2 (1 point)

Réalisez une classe Xcarre sans attribut, dérivée de Fonction représentant la fonction qui à tout réel $x$ associe $x^2$.

"Solution"

public class Xcarre extends Fonction
{
    public double getImage(double x)
    {
        return x * x;
    }
}

C3 (2 points)

On souhaite que la méthode main suivante…

public static void main(String[] args)
{
    Fonction f = new Xcarre();
    System.out.println(f.getNom());
}

…produise l’affichage

Fonction carré

Donnez le code complet de la ou des méthodes concrètes et / ou abstraites à ajouter aux classes Fonction et Xcarre pour obtenir ce résultat sans ajouter d’attribut à ces classses.

"Solution"

Dans Fonction :

public abstract String getNom();

Dans Xcarre :

public String getNom()
{
    return "Fonction carré";
}

Partie D

La classe Fraction représente une fraction (un nombre rationnel) ayant un dénominateur et un numérateur.

public class Fraction
{
    private int num;
    private int den;

    public Fraction(int numerateur, int denominateur) throws  DenZero
    {
        if(denominateur == 0) throw new DenZero();
        this.num = numerateur;
        this.den = denominateur;
        normalise();
    }

    public int getDenum() {return den;}

    public int getNum() {return num;}

    public void normalise()
    {
        // Code classifié très secret cosmique
    }

    public Fraction add(Fraction f)
    {
        // À comlpléter
    }

    public String toString()
    {
        return num + " / " + den;
    }
}

Regardez attentivement le code du constructeur. Il lève une exception de type DenZero si par malheur on tente de l’utiliser pour créer une fraction ayant un dénominateur nul. Dans le cas contraire, il initialise les attributs et appelle une méthode de normalisation. Le code de cette méthode est ultra secret et ne sera pas révélé ici. Il permet de normaliser la fraction de manière à ce que le dénominateur soit toujours positif et de la simplifier de manière à minimiser les valeurs du numérateur et du dénominateur. Par exemple, si les valeurs données sont 4 et 12, après simplification au aura 1 / 3.

La classe DenZero est définie ainsi :

public class DenZero extends Exception
{
    public String toString()
    {
        return "Dénominateur nul";
    }
}

D1 (2 points)

Complétez le fonction testFrac suivante de manière à ce qu’elle crée une instance de Fraction représentant la fraction $a/b$ et affiche sa représentation à l’aide de la méthode toString. Dans le cas où le constructeur de la classe Fraction lève une exception de type DenZero, le message "ERREUR : Dénominateur nul" doit s’afficher.

public static void testFrac(int a, int b)
{
    // À compléter
}

"Solution"

public static void testFrac(int a, int b)
{
    try
    {
        Fraction r = new Fraction(a,b);
        System.out.println(r.toString());
    }
    catch(DenZero e)
    {
        System.out.println("ERREUR  : " + e);
    }
}

D2 (2 points)

On rappelle que la somme de deux fractions valides (avec dénominateurs non nuls) $a/b$ et $c/d$ a pour résultat la simplification (avec la méthode normalize) de $(ad + bc) / bd$.

Complétez une méthode add de la classe Fraction en faisant en sorte qu’elle retourne la somme de la fraction courante et de cette désignée par le paramètre f. La fraction courante ne doit pas être modifiée. Si l’exception DenZero est levée lors de la construction du résultat (Ça ne devrait pas se produire, mais il faut le prévoir quand même), la méthode add doit lever une exception de type RuntimeException avec message "Erreur inattendue" passé en argument à son constructeur.

public Fraction add(Fraction f)
{
    // À compléter
}

"Solution"

public Fraction add(Fraction f)
{
    int n = (getNum() * f.getDenum()) + (f.getNum() * getDenum());
    int d = getDenum() * f.getDenum();
    try
    {
        return new Fraction(n, d);
    }
    catch (DenZero e)
    {
        throw new RuntimeException("Erreur inattendue");
    }
}

Partie E

Un multi-ensemble est une structure de donnée pouvant contenir des éléments, comme un ensemble, mais à la différence d’un ensemble, chaque élément peut avoir plusieurs occurrences. Par exemple, {2, 5, 5, 56} est un multi-ensemble dont les éléments sont 2, 5 et 56. L’élément 5 a deux occurrences, alors que les autres en ont une seule.

La classe MultiInt représente un multi-ensemble d’entiers naturels (c’est à dire supérieurs ou égaux à 0).

public class MultiInt
{
    // Attributs à completer

    public MultiInt(int max)
    {
        // À compléter
    }

    public void add(int e)
    {
				// À compléter
    }

    public void remove(int e)
    {
				// À compléter
    }
    // ...
}

La classe MultiInt comporte d’autres méthodes, mais seules celles qui sont mentionnées plus haut nous intéressent dans cet exercices.

Le constructeur permet de créer un multi-ensemble pouvant contenir les éléments compris entre 0 et max, chacun pouvant n’avoir aucune occurrence ou avoir un nombre quelconque d’occurrences.

E1 (4 points)

Vous devez donner le ou les attributs de la classe et le code du constructeur et des deux méthodes. Si e est un entier compris entre 0 et max et m est une instance de MultiInt construite de la manière suivante…

MultiInt m = new MultiInt(max);

…alors :

m.add(e) ajoute une occurrence de e dans le multi-ensemble désigné par m,
m.remove(e) retire une occurrence de e s’il en reste au moins une et sinon n’a aucun effet.

Vous devez essayer de trouver une solution permettant de minimiser la complexité en temps (en fonction du nombre d’éléments du multi-ensemble courant) des méthodes add et remove. Vous devez également donner l’ordre de grandeur asymptotique des ces complexité (constante ou logarithmique ou linéaire ou quadratique ou autre …) en justifiant brièvement votre réponse.

"Solution"

public class MultiInt
{
    private int[] tab;

    public MultiInt(int max)
    {
        tab = new int[max+1];
    }

    public void add(int e)
    {
        tab[e]++;
    }

    public void remove(int e)
    {
        if(tab[e]>0) tab[e]--;
    }

    public int count(int e)
    {
        return tab[e];
    }
}

Complexité :

add : $\Theta(1)$ (temps constant)
remove : $\Theta(1)$ (temps constant)

PPC : Test d’auto-évaluation sur la partie B

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Objectif

Entraînement et évaluation partielle des vos compétences en modélisation.

Prérequis

Parties A et B

Question 1

On appelle séquenceur d’un mot binaire $a_1 a_2 … a_n$ le mot binaire $x_2 … x_n$ tel que $x_i = 1$ si et seulement si $a_{i-1} \neq a_i$.

Voici un exemple de mot binaire et de son séquenceur.

mot m :           001110000000
séquenceur de m :  01001000000

On considère les variables $A_1, …, A_n$ et $X_2, …, X_n$ ayant toutes pour domaines $\{0,1\}$.

Vous devez spécifier un réseau de contraintes $T_n$ tel que toute assignation $A_1=a_1,…,A_n=a_n$, $X_2=x_2,…,X_n=x_n$ satisfait $T_n$ si et seulement si le mot binaire $x_2 … x_n$ est le séquenceur du mot binaire $a_1 a_2 … a_n$.

Par exemple, l’assignation $A_1=1, A_2=0, A_3=1, X_2=1, X_3=1$ satisfait $T_3$ car 11 est le séquenceur de 101. Par contre l’assignation $A_1=1, A_2=0, A_3=1, X_2=0, X_3=1$ ne satisfait pas $T_3$ car 01 n’est pas le séquenceur de 101.

$T_n$ est constitué de $n-1$ contraintes nommées $q_1, …, q_{n-1}$.

Précisez les variables reliées par chaque contrainte. Donnez une spécification en extension et une spécification en compréhension (avec des opérations arithmétiques ou logiques) d’une de ces contraintes.

Réponse

Chaque contrainte $q_i$ relie les variables $A_i$, $A_{i+1}$ et $X_{i+1}$.

Exemple de spécification de $q_i$ en compréhension : $X_{i+1} = |A_{i}-A_{i+1}|$.

Spécification de $q_i$ en extension : sur $A_i$, $A_{i+1}$, $X_{i+1}$ : $\{(0,0,0),(1,1,0),(0,1,1),(1,0,1)\}$.

Question 2

En supposant que $n>3$, quelles contraintes faut-il ajouter au réseau $T_n$ de la question précédente pour exprimer que le mot binaire $a_1 a_2 … a_n$ comporte exactement une séquence de 3 bits à 1 consécutifs, tous les autres bits étant à 0 ?

On entend par là que si on note le réseau $T’_n$ le réseau obtenu en ajoutant à $T_n$ ces nouvelles contraintes, alors toute assignation partielle $A_1=a_1,…,A_n=a_n$ a une extension satisfaisant $T’_n$ si et seulement si le mot binaire $a_1 a_2 … a_n$ comporte exactement une séquence de 3 bits à 1 consécutifs, tous les autres bits étant à 0, comme dans les exemples suivants : 00111100, 000111, 111000000.

Les nouvelles contraintes sont à donner en compréhension.

Réponse

$\sum_{i=1}^n A_i = 3$ (Il y a trois bits à 1).
$\sum_{i=2}^n X_i \leq 2$ (Il y a au plus deux transitions).
$A_1 + A_n \leq 1$ (Il ne doit pas y avoir un bit à 1 aux deux extrémité)

Question 3

On considère un dirigeable dont la nacelle est scindée en trois parties : une cabine destinée aux passagers au milieu et deux compartiments de fret, nommés A et B, aux extrémités. Parmi $N$ objets, numérotés de 1 à $N$ et de poids $w_1, …, w_n$ , au moins $K$ doivent être embarqués en respectant les conditions suivantes :

La somme des poids des objets embarqués dans le compartiment A doit être égale à la somme des poids des objets embarqués dans le compartiment B.
La somme des poids des objets embarqués dans les deux compartiments ne doit pas dépasser une valeur W.

Les valeurs $K$ et W, ainsi que les poids des $N$ objets susceptibles d’être embarqués, sont des données connues. Vous devez modéliser ce problème sous la forme d’un réseau de contraintes utilisant exclusivement des variables à domaine {0,1}. Vous devez utiliser des contraintes arithmétiques linéaires construites à l’aide de sommes, produits d’une variable par une constante, opérateurs de comparaison ($=$, $\neq$, $<$, $>$, $\leq$, $\geq$). Précisez bien le rôle et la signification d’une assignation à 1 de chaque variable.

Réponse

Variables :

$A_1, … ,A_N$ de domaine $\{0,1\}$. $A_N=1$ signifie que l’objet numéro $i$ va dans le compartiment A.
$B_1, … ,B_N$ de domaine $\{0,1\}$. $B_N=1$ signifie que l’objet numéro $i$ va dans le compartiment B.

Contraintes :

$(\sum_{i=1}^n A_i) + (\sum_{i=1}^n B_i) \geq K$ (au moins $K$ objets embarqués)
$\sum_{i=1}^n w_i A_i = \sum_{i=1}^n w_i B_i$ (équilibre des charges)
$\sum_{i=1}^n w_i A_i + \sum_{i=1}^n w_i B_i \leq W$ (charge maximale autorisée)
Pour tout $i\in 1..N$, $A_i + B_i < 2$ (un objet est est embarqué dans un seul compartiment ou n’est pas embarqué)

Question 4

On considère 8 variables $X_1, X_2, Y_1, Y_2$, $X’_1, X’_2, Y’_1, Y’_2$ ayant toutes pour domaine l’ensemble $0..N$ des entiers naturels compris entre 0 et $N$.

Une assignation de ces variables représente deux rectangles situés dans un repère cartésien discret avec les conventions suivantes :

$X_1, Y_1$ sont les coordonnées du coin inférieur gauche du premier rectangle.
$X_2, Y_2$ sont les coordonnées du coin supérieur droit du premier rectangle.
$X’_1, Y’_1$ sont les coordonnées du coin inférieur gauche du deuxième rectangle.
$X’_2, Y’_2$ sont les coordonnées du coin supérieur droit du deuxième rectangle.

La figure ci-dessous représente un exemple de positions et formes des deux rectangles, mais il y a un très grand nombre d’autres possibilités.

Vous devez spécifier les contraintes qui expriment que les deux rectangles se recouvrent (l’intersection entre les 2 est non vide). La ou les contraintes à écrire peuvent combiner des opérations arithmétiques (additions, soustractions, comparaisons) et logiques (et, non).

On suppose que $X_2 > X_1$, $Y_2 >Y_2$, $X’_2 > X’_1$ et $Y’_2 >Y’_2$.

Réponse

$X’_1 < X_2$,

$X_1 < X’_2$,

$Y’_1 < Y_2$,

$Y_1 < Y’_2$

Question 5

On considère un échiquier (une grille) de N par N. Une pièce appelée cavalier peut se déplacer sur cette grille en se décalant de deux positions horizontalement et d’une verticalement ou de deux positions verticalement et d’une horizontalement. La figure ci-dessous donne deux exemples indépendants dans lesquels la grosse pastille désigne la position initiale d’un cavalier et les petites pastilles désignent les cases pouvant être atteintes par ce cavalier.

On considère les variables $X_1, Y_1, X_2, Y_2, V, H$ de domaines respectifs $1..N$, $1..N$, $1..N$, $1..N$, $\{-2,-1,1,2\}$, $\{-2,-1,1,2\}$.

Donnez en compréhension les contraintes qui spécifient qu’un cavalier situé en position $(X_1,Y_1)$ peut aller en $(X_2,Y_2)$ en se déplaçant de $H$ cases horizontalement et de $V$ case verticalement.

Réponse

$|X_1-X_2| = H$
$|Y_1-Y_2| = V$
$H\neq V$

Question 6

On numérote de la manière suivante les 8 déplacements réalisables par un cavalier sous réserve que les cases de destination soient dans les limites de l’échiquier.

On ajoute une variable $D$ de domaine $1..8$ au réseau de contraintes précédent. Donnez en extension la contrainte à ajouter entre $V$, $H$ et $D$ pour que dans toute assignation satisfaisant toutes les contraintes, $D$ aie pour valeur le numéro du déplacement correspondant aux valeurs de $V$ et $H$.

Réponse

Sur $V,H,D$ : $\{(2,1,1),(1,2,2),(-1,2,3),(-2,1,4),(-2,-1,5),(-1,-2,6),(1,-2,7),(2,-1,8)\}$

POO : Test Partie C

En licence pro MI AW

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

On considère l’interface suivante :

public interface RandGen
{
    public void setMin(double min);
    public void setMax(double max);
    public double getMin();
    public double getMax();
    public String getLaw();
    public double draws();
}

Les classes qui implémentent cette interface ont vocation à produire des nombres aléatoires de type double compris entre deux valeurs pouvant être déterminées par les méthodes setMin et setMax et pouvant être consultées à l’aide des méthodes getMin et getMax. Ces classes doivent aussi disposer d’une méthode getLaws qui retourne une chaîne de caractères décrivant la loi de probabilité utilisée et d’une méthode draws dont le rôle est de produire une valeur aléatoire dans l’intervalle getMin() .. getMax().

La classe abstraite GenericRandGen implémente l’interface RandGen.

public abstract class GenericRandGen implements RandGen
{
    private double min;
    private double max;

    public GenericRandGen()
    {
        this.min = 0.0; this.max = 1.0;
    }

    public void setMin(double min) {this.min = min;}

    public void setMax(double max) {this.max = max;}

    public double getMin() {return this.min;}

    public double getMax() {return this.max;}

    public abstract String getLaw();

    public abstract double draws();

    public String toString()
    {
        return "Générator " + getLaw() + " in [" + min + "," + max + "]";
    }

    public double[] sample(int n)
    {
        // À compléter
    }
}

La méthode sample produit un tableau de longueur n rempli de valeurs alétoires produites par la méthode draws.

Q1 (1.5 point)

Complétez la méthode sample de la classeGenericRandGen.

public double[] sample(int n)
{
    // À compléter
}

Merci d’envoyer votre réponse à Olivier Bailleux via teams.

Q2 (1.5 points)

Complétez la classe UniformGen qui représente un générateur aléatoire permettant de produire des valeurs selon une loi de probabilité uniforme. Ces valeurs peuvent être obtenues à partir de la méthode Math.random() qui produit une valeur comprise entre 0.0 et 1.0 selon une loi uniforme.

public class UniformGen extends GenericRandGen
{
    // À compléter
}

Merci d’envoyer votre réponse à Olivier Bailleux via teams.

Q3 (2 points)

Réalisez une méthode main, situé dans une classe Main, qui :

Crée un générateur de type UniformGen.
Initialise à 1.0 et 3.0 les bornes minimum et maximum de l’intervalle des valeurs pouvant être produites par ce générateur.
Utilise la méthode sample pour produire une tableau de 10 nombres aléatoires.
Affiche à l’écran les valeurs récupérées dans ce tableau.

public class Main
{
    public static void main(String[] args)
    {
        // À compléter
    }
}

Merci d’envoyer votre réponse à Olivier Bailleux via teams.

PPC : test d’autoévaluation partie A

Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Test d’auto-évaluation sur la partie A

Objectif

Vérifier si vous avez assimilé de manière approfondie les notions de la partie A

Prérequis

Partie A

Question 1

Pour chacune de ces deux contraintes, dites si elle est donnée en extension et/ou en compréhension et/ou sous forme énumérative. On suppose que les variable ont toutes pour domaines ${1,2,3}$.

$A > C+1$
sur $A,B,C$, ${(1,1,1),(1,2,1),(2,1,2)}$

"Réponse"

La première contrainte est en compréhension. La deuxième est en extension. Elle est donnée sous forme énumérative. (Les deux termes sont équivalents.)

Question 2

Le réseau de contraintes suivant a-t-il des solutions ? Si oui, donnez les.

![](

"Réponse"

Ce réseau n’a pas de solution. Il est incohérent.

Question 3

Le réseau de contraintes suivant a-t-il des solutions ? Si oui, donnez les.

"Réponse"

$A=\alpha, B=\beta, C=\alpha, D=\beta$
$A=\beta, B=\alpha, C=\beta, D=\alpha$

Question 4

On dit que deux contraintes sont équivalentes si et seulement si elles relient les mêmes variables, de même domaines, et sont satisfaites par les même assignations de ces variables.

Soit $A$ et $B$ deux variables à domaine ${0,1}$. Les contraintes $A=\neg B$ et $A\vee B$ sont elles équivalentes ?

"Réponse"

Non, car l’assignation $A=1,B=1$ falsifie la première contrainte et satisfait la deuxième.

Question 5

Soit $A$ et $B$ deux variables à domaine ${0,1}$. Les contraintes $A=\neg B$ et $(A\vee B)\wedge(\neg A\vee \neg B)$ sont elles équivalentes ?

"Réponse"

Oui.

Question 6

Soit la contrainte $10 A + 5 B + C \leq 11$, où $A$, $B$ et $C$ ont pour domaine ${0, 1}$.

Donnez une assignation partielle $I$ qui falsifie cette contrainte et une assignation partielle $J$ qui la satisfait.

"Réponse"

$I$ : $A=1, B=1$.

$J$ : $A=0$ ou $B=0$ ou toute extension de ces assignations.

Question 7

Soient $A$ et $B$ deux variables ayant pour domaine ${0,1}$. Donnez une contrainte équivalente à $A = \neg B$ spécifiée en compréhension en utilisant uniquement des opérateurs arithmétiques +, -, = et des constantes entières (0, 1, …).

"Réponse"

$A = 1 – B$ ou $B= 1 – A$ ou $A+B = 1$.

Question 8

Soient les variables $A$ et $B$ de domaine ${0,1}$ et les variables $X$ et $Y$ de domaine ${0,2}$.

On considère :

la contrainte $q : A\vee B$,
et le réseau $r : A\neq X, B\neq Y, X\neq Y$.

Soit $I$ une assignation des variable $A,B$, qui est aussi une assignation partielle des variables de $r$. Parmi les affirmations suivantes, lesquelles sont vraies ?

Si $I$ satisfait $q$ alors il existe une extension de $I$ qui satisfait $r$.
Si il existe une extension de $I$ qui satisfait $r$ alors $I$ satisfait $q$.
Si $I$ falsifie $q$ alors $I$ (vu comme une assignation partielle des variables de $r$) falsifie $r$.
Si $I$ satisfait $q$ alors $I$ (vu comme une assignation partielle des variables de $r$) satisfait $r$.

"Réponse"

Oui. On peut vérifier que pour chacune des assignations qui satisfont $q$, c’est à dire ${A=0,B=1}$, ${A=1,B=0}$, et ${A=1, B=1}$, il existe une valeur de $X$ et une valeur de $Y$ qui permettent de satisfaire $r$.
Oui. Il existe une extension de $I$ qui satisfait $r$ si $I={A=0,B=1}$ ou si $I={A=1,B=0}$ ou si $I={A=1, B=1}$. (et pas si $I={A=0, B=0}$). Ces trois assignations satisfont $q$.
Oui. La seule assignation $I$ qui falsifie $q$ est ${A=0, B=0}$. Cette assignation falsifie $r$.
Non. Par exemple, $A=1,B=1$ satisfait $q$ mais son extension $A=1,B=1,X=2,Y=2$ falsifie $r$.