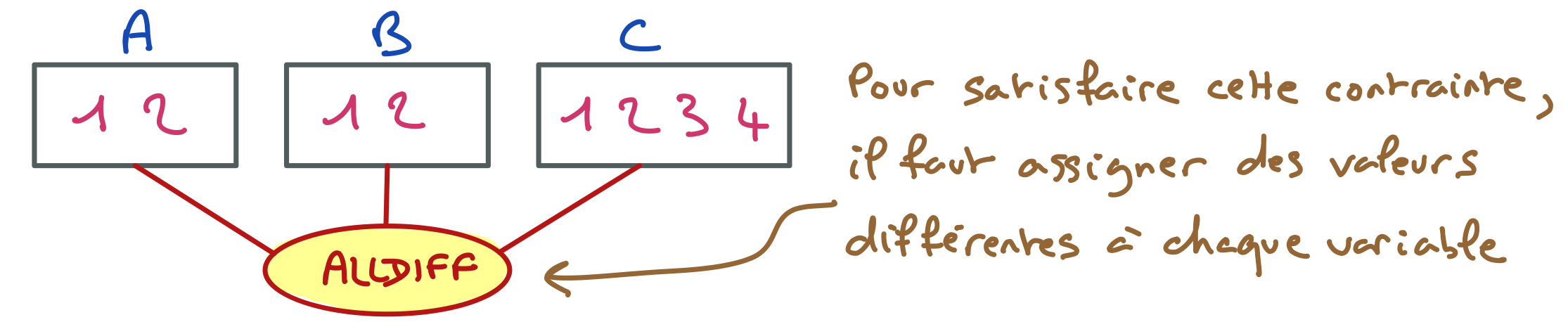Archives de catégorie : PPC

Programmation par contraintes : partie C

Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Partie C : Le filtrage par cohérence de domaines

Objectif

Être capable de restaurer la cohérence de domaines sur un réseau de contraintes. Comprendre en profondeur en quoi consiste la restauration de cohérence de domaines sur une seule contrainte et sur un réseau de contraintes.

Prérequis

Partie A.

C1 : Cohérence de domaine

Ce que nous allons voir ici est une forme simple de raisonnement automatique permettant de réaliser des déductions dont les conclusions consistent à retirer des valeurs des domaines de certaines variables pour simplifier un réseau de contraintes. Le système déductif utilisé est élémentaire. Il travaille avec une seule contrainte à la fois. Les informations exploitées pour faire la déduction sont une contrainte et les contenus des domaines des variables reliées par cette contrainte. Le résultat de la déduction, i.e., sa conclusion sont les contenus des mêmes domaines dans lesquels certaines valeurs ont été (si applicable) retirées.

Notion de support

Soit q une contrainte, V(q) l’ensemble des variables reliées par q, v une variable appartenant à V(q) et x un élément du domaine de v. On appelle support de l’assignation v=x toute assignation complète de V(q) qui étend {v=x} et satisfait q.

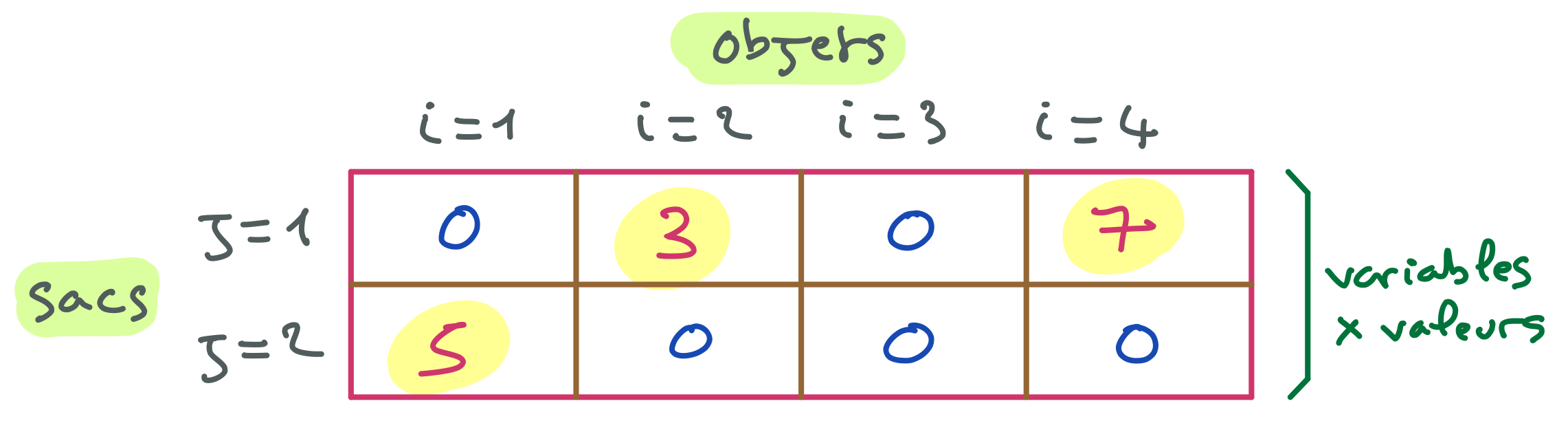
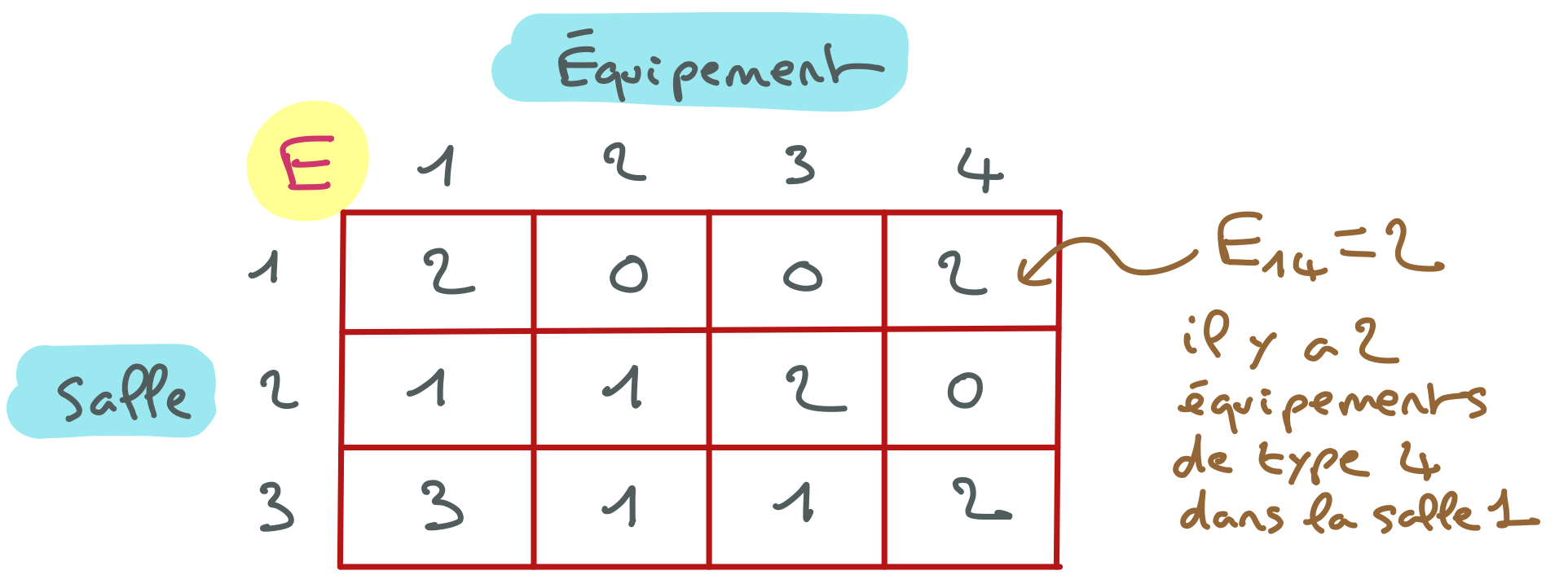
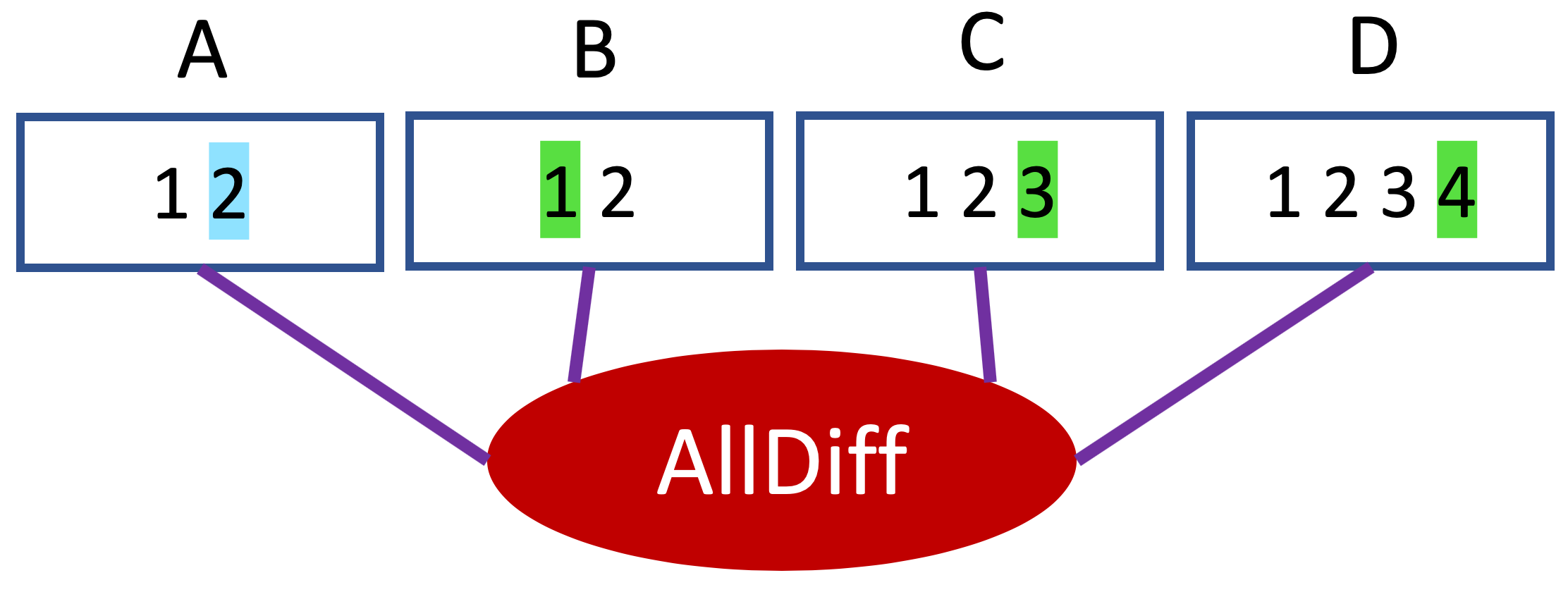
Dans l’exemple ci-dessous, A=2 a un seul support : {A=2, B=1, C=3, D=4}.

Cohérence de domaine

Dans un réseau de contraintes, la cohérence de domaines est respectée si et seulement si pour toute variable v et toute valeur x du domaine de v, v=x a un support pour toutes les contraintes dans lesquelles la variable v intervient.

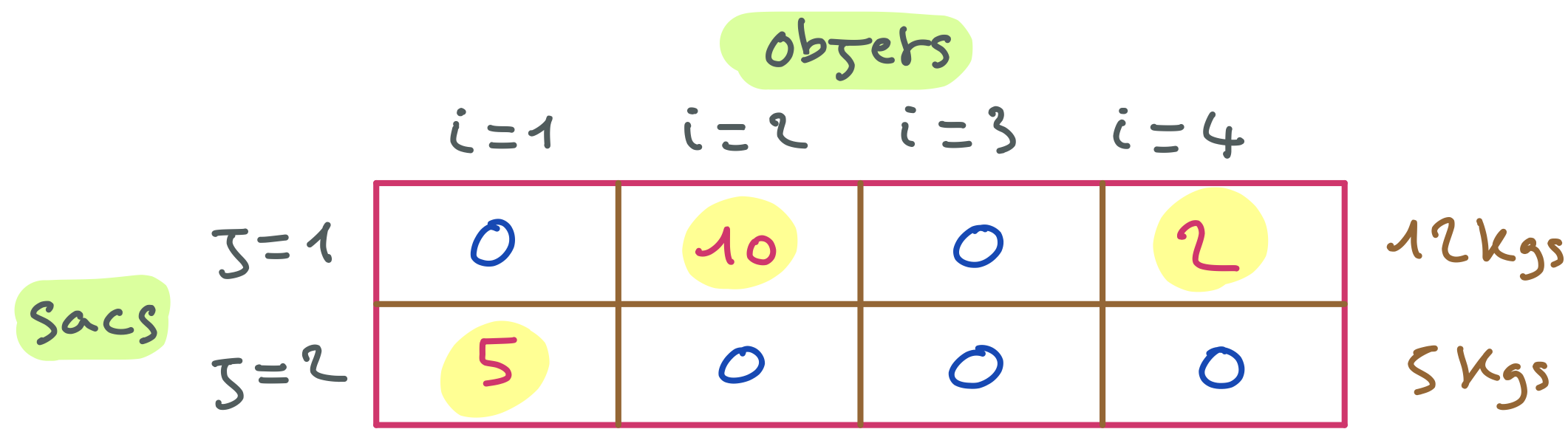
Par exemple, le réseau constitué de la seule contrainte ci-dessous ne respecte pas la cohérence de domaine car C=1 n’a pas de support.

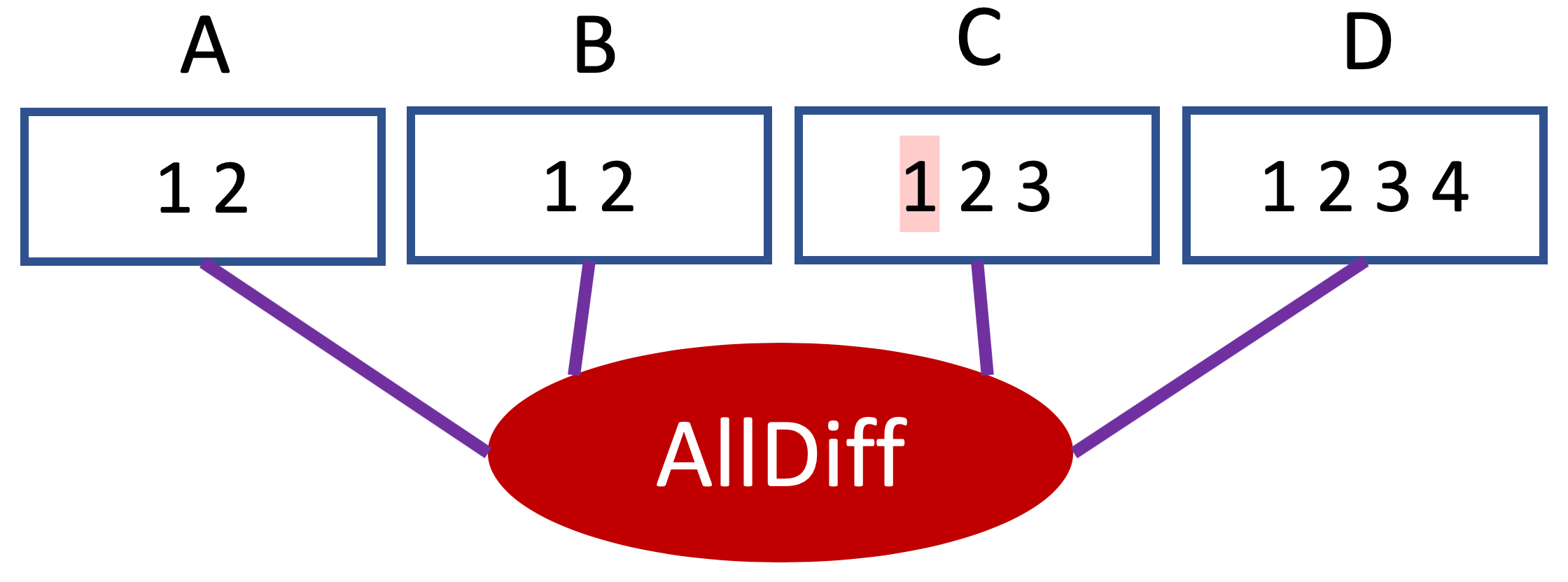
Si on assigne la valeur 1 à C, alors quelles que soient les valeurs des autres variables, la contrainte ne peut être satisfaite.

Exercices de découverte

C-dec-10

Soit la contrainte $A < B$ où les variables $A$ et $B$ ont toutes les deux pour domaine ${1,2,3}$. Quels sont les supports de $A=1$ ?

"Solution"

${A=1,B=2}$ et ${A=1,B=3}$.

C-dec-10

Soit la contrainte $A < B$ où les variables $A$ et $B$ ont toutes les deux pour domaine ${1,2,3}$. Y a-t-il une valeur du domaine de A n’ayant aucun support pour cette contrainte ? Si oui laquelle et pourquoi ?

"Solution"

$A = 3$. Parce que si $A$ vaut 3, il n’existe aucune valeur dans le domaine de $B$ permettant de satisfaire la contrainte.

C2 : Restaurer la cohérence de domaine

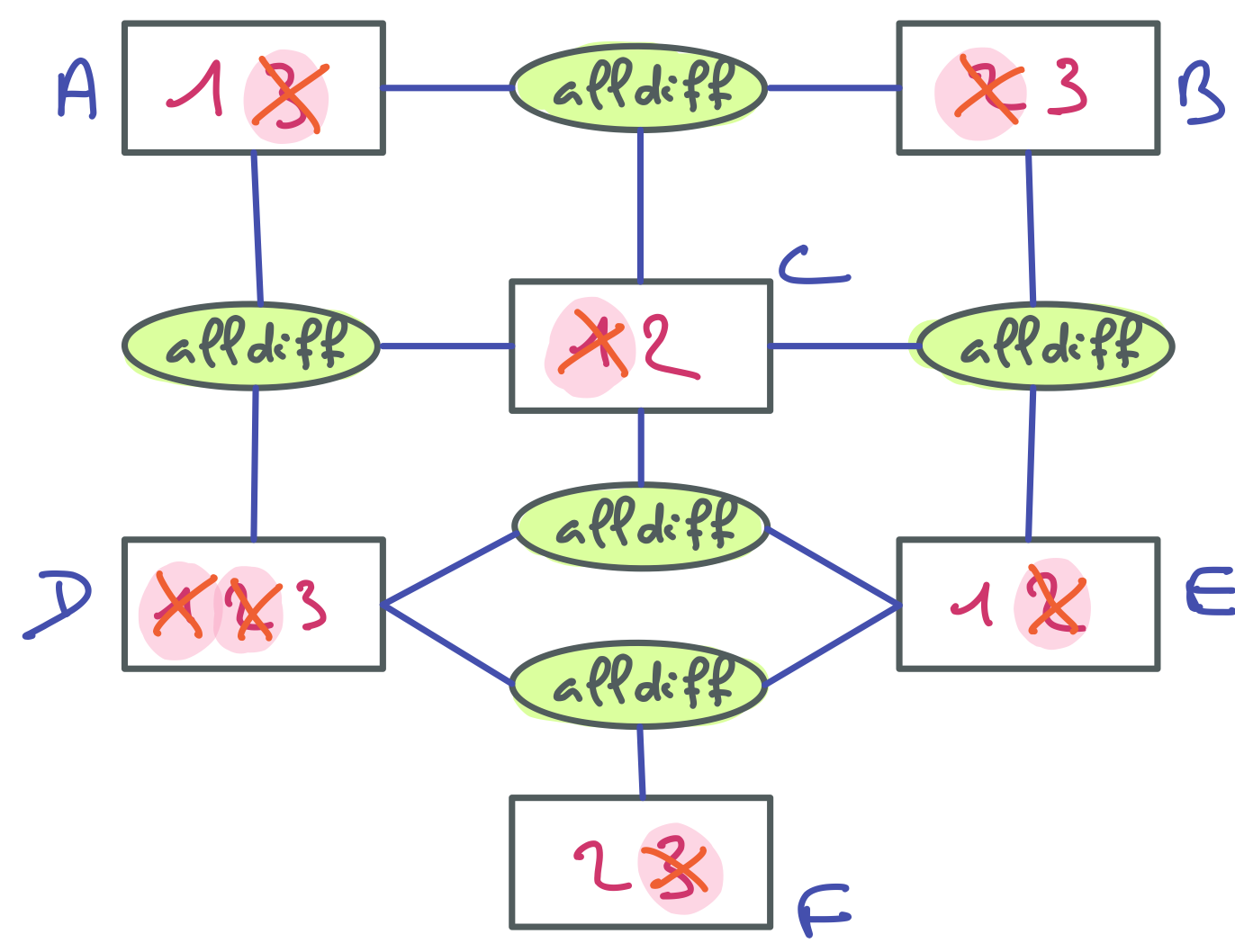
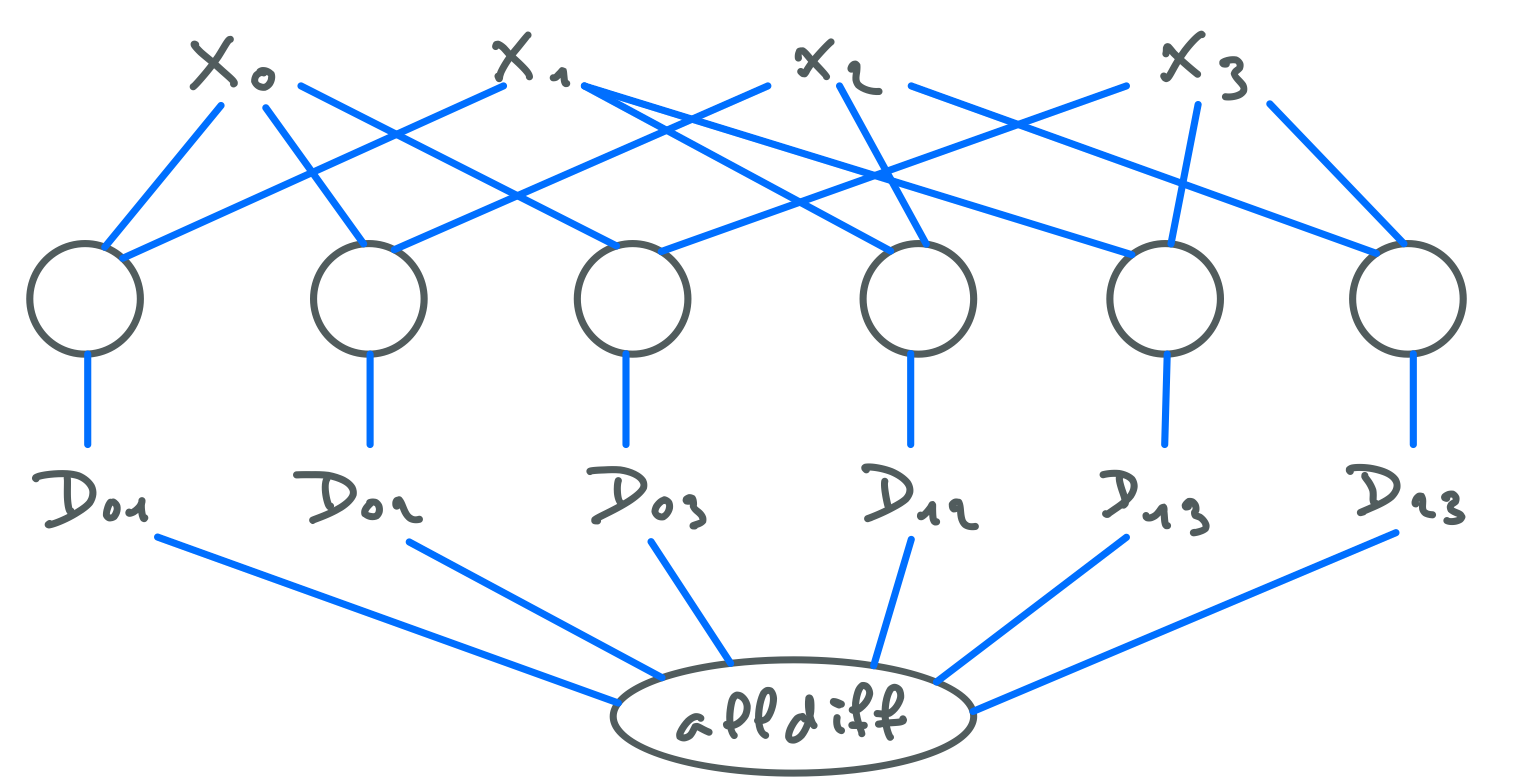
Restaurer la cohérence de domaines consiste à retirer de chaque domaine toutes les valeurs qui n’ont pas de support pour au moins une contrainte du réseau. Par exemple, dans le réseau ci-dessous qui ne comporte qu’une seule contrainte, C=1, C=2, D=1, D=2, D=3 n’ont pas de support.

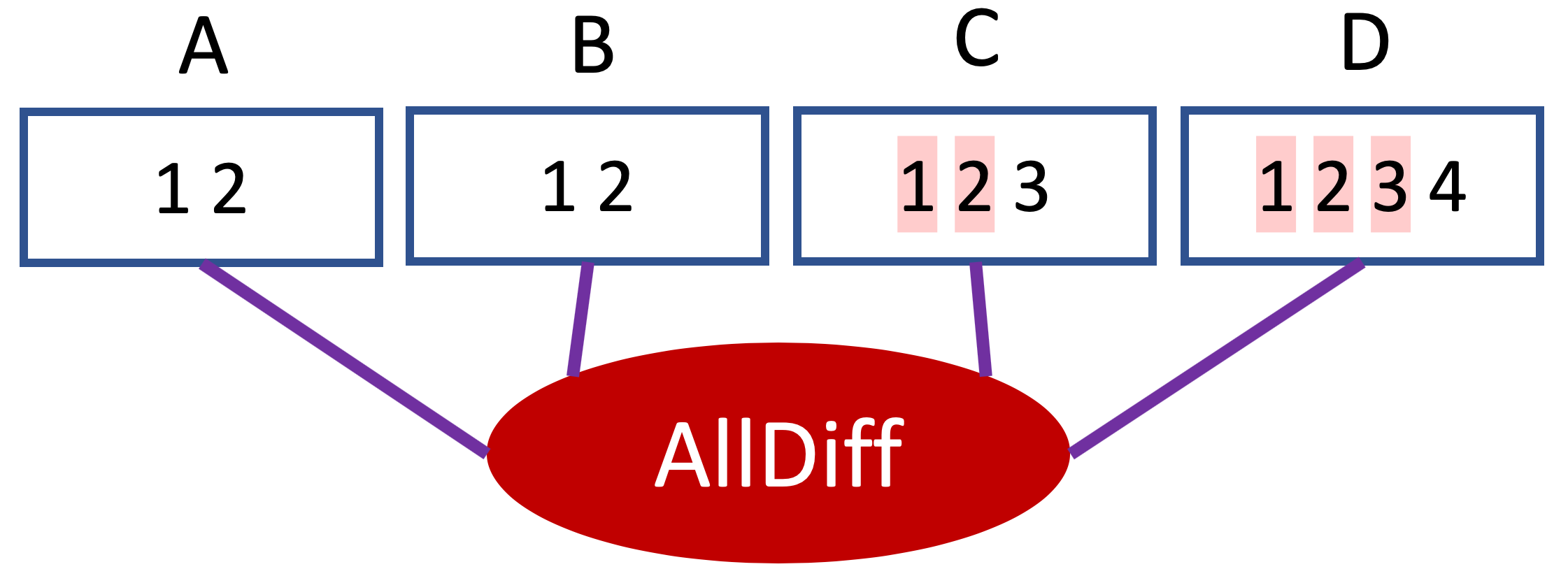
Vous pouvez vérifier que dans aucune des assignations complètes de A, B, C, D permettant de satisfaire la contrainte alldiff, on a C=1 ou C=2 ou D=1 ou D=2 ou D=3. Donc ces valeurs peuvent être retirées des domaines concernés et on obtient le résultat suivant.

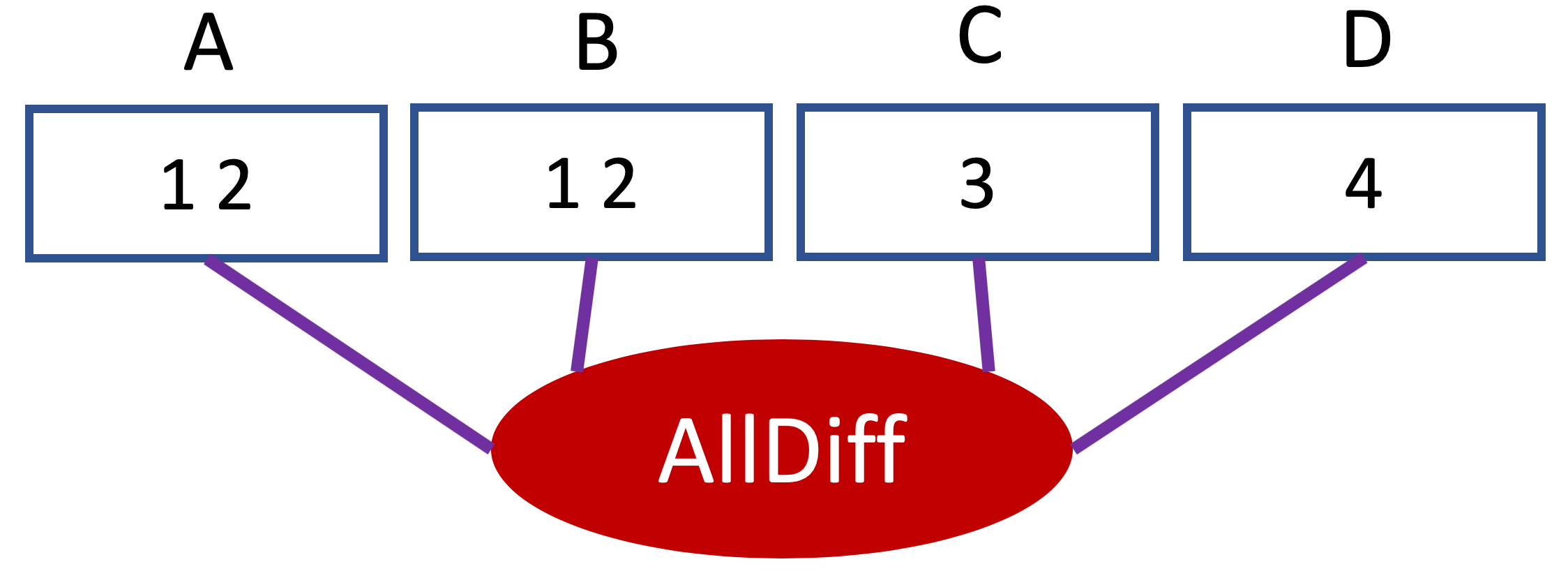
La contrainte alldiff est « filtrée », et comme c’est la seule contrainte du réseau, le réseau respecte maintenant la cohérence de domaines : chaque valeur de chaque domaine de chaque variable a un support pour chaque contrainte concernée par cette variable.

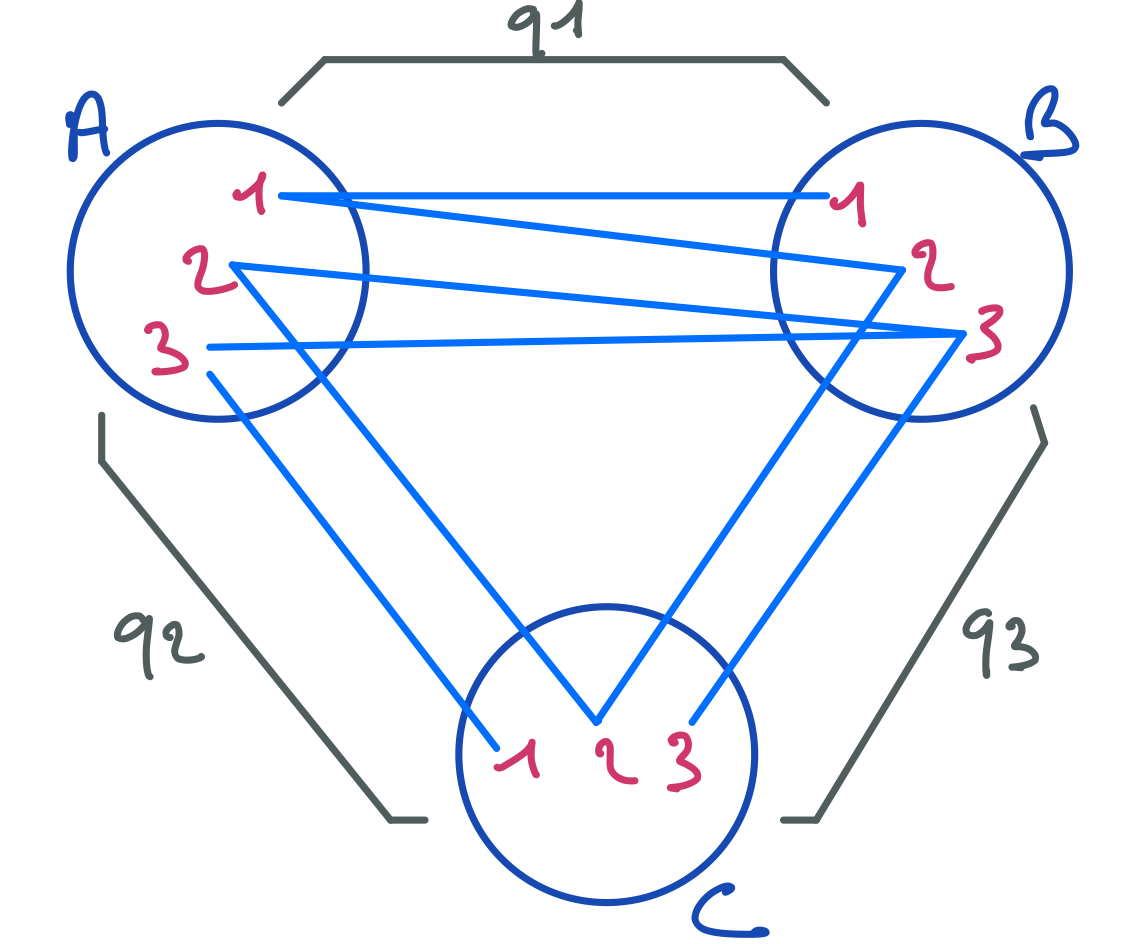
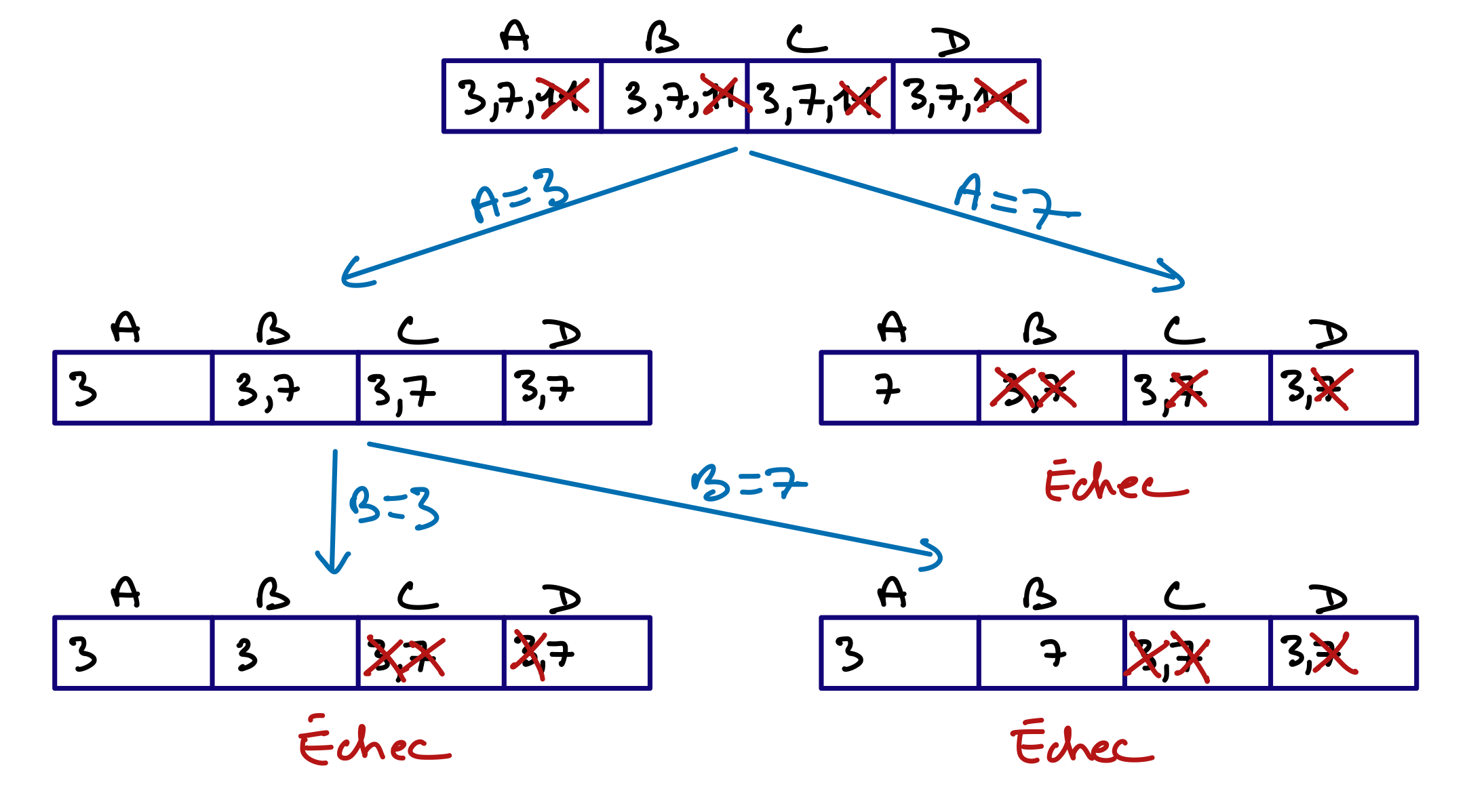
Voici un autre exemple. Nous allons restaurer la cohérence de domaine sur un réseau de contraintes représenté sous forme énumérative. Comme toutes les contraintes sont binaires, c’est-à-dire relient deux variables, le réseau peut se représenter graphiquement, ce qui permet de visualiser plus facilement les étapes. Voici le réseau initial.

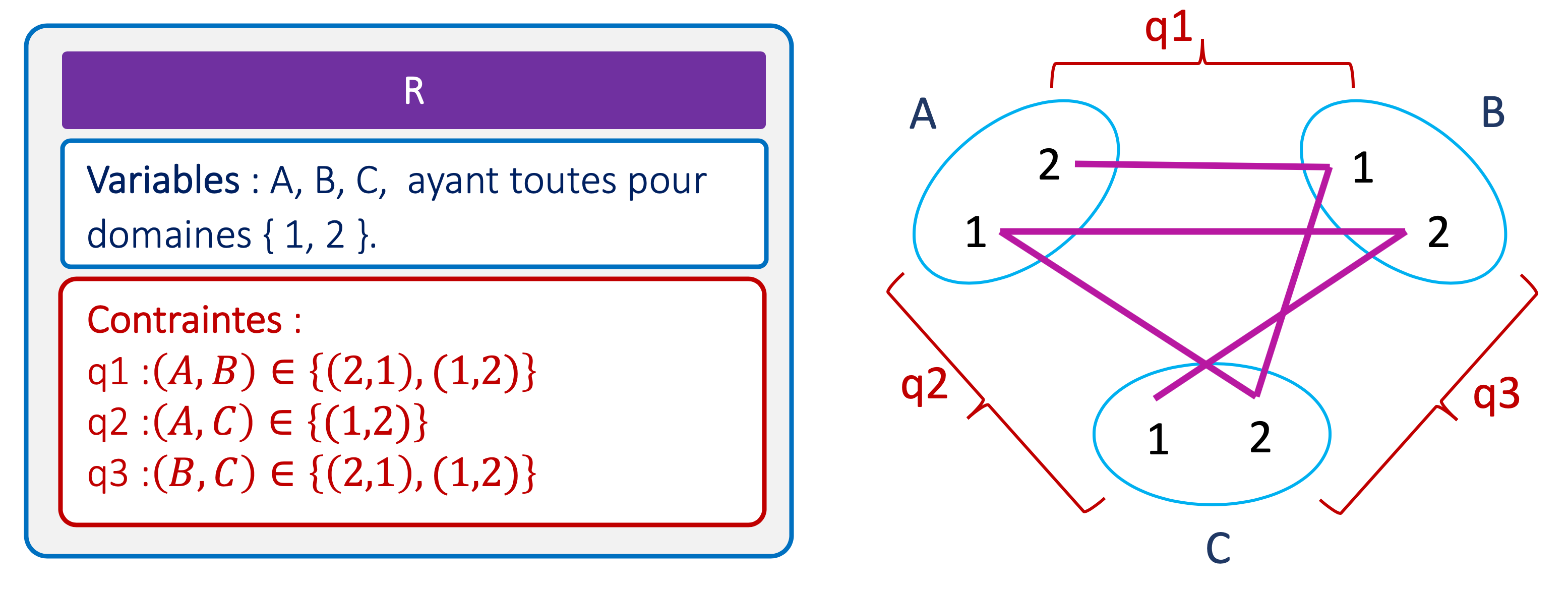
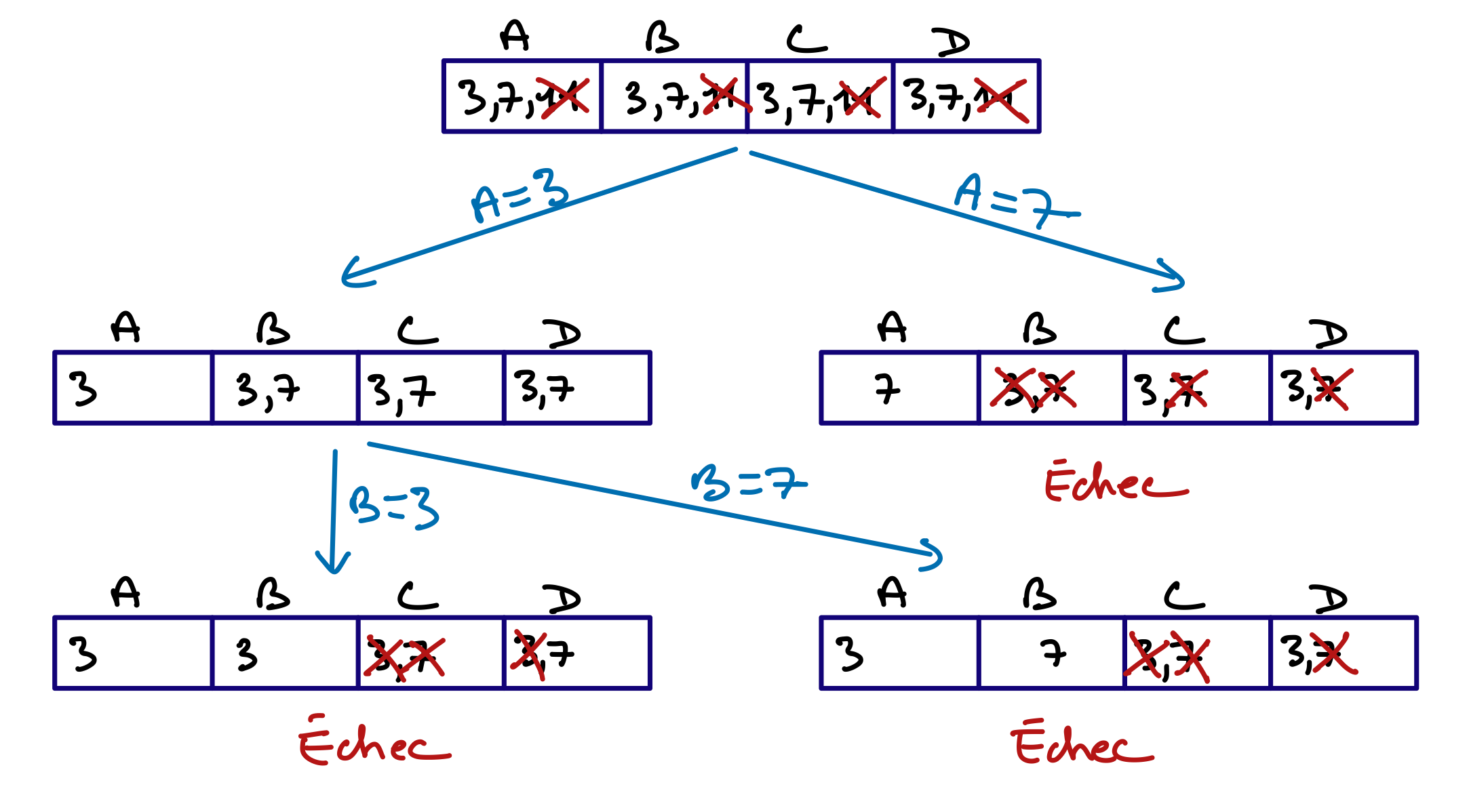
Voici les différentes étapes du filtrage.

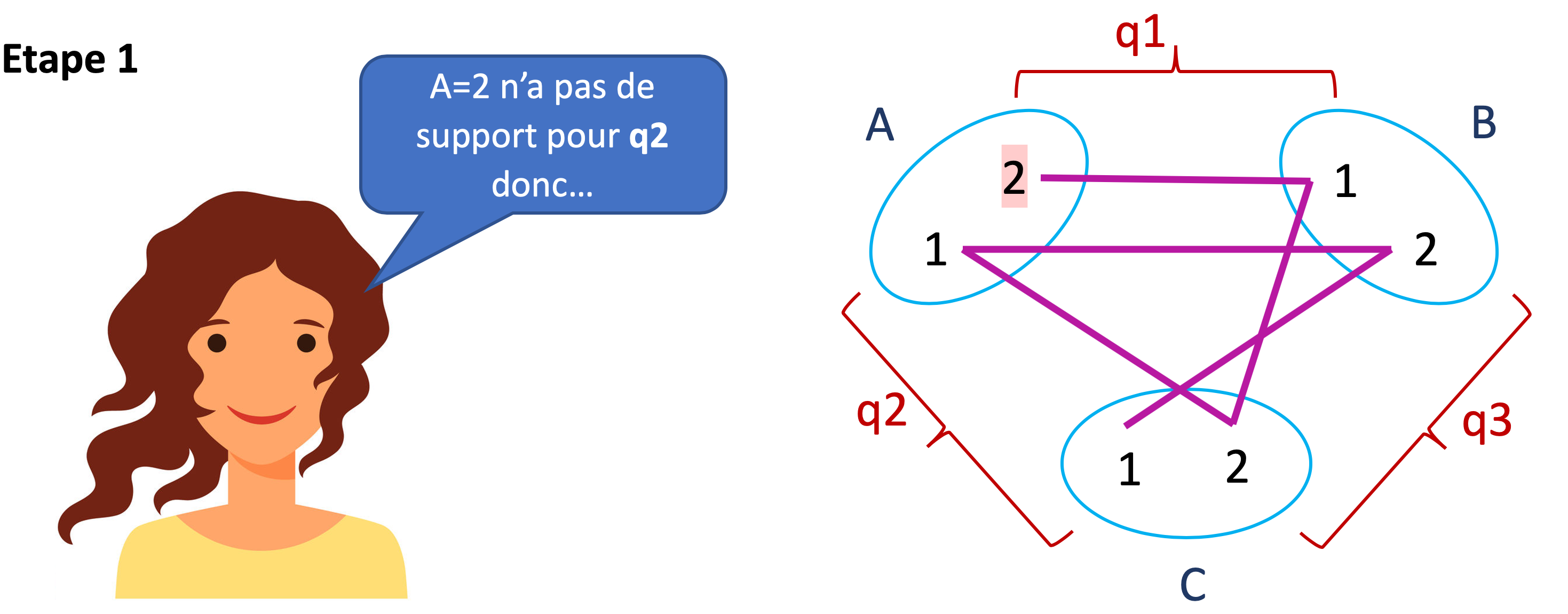
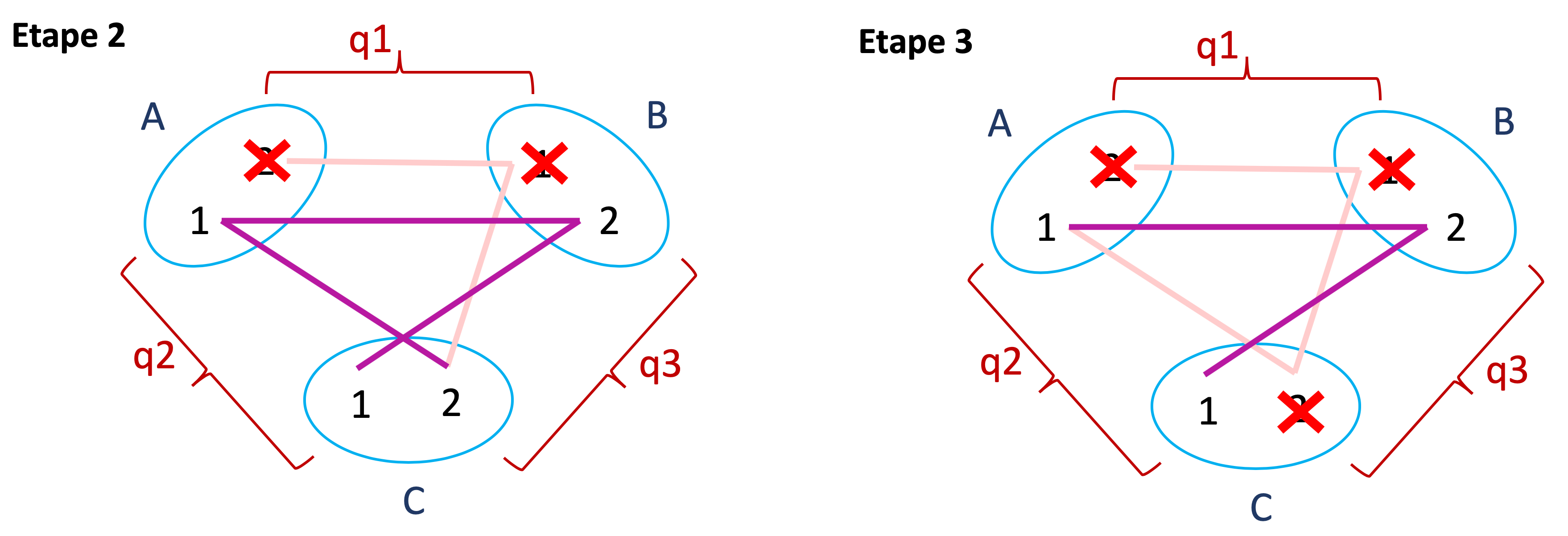
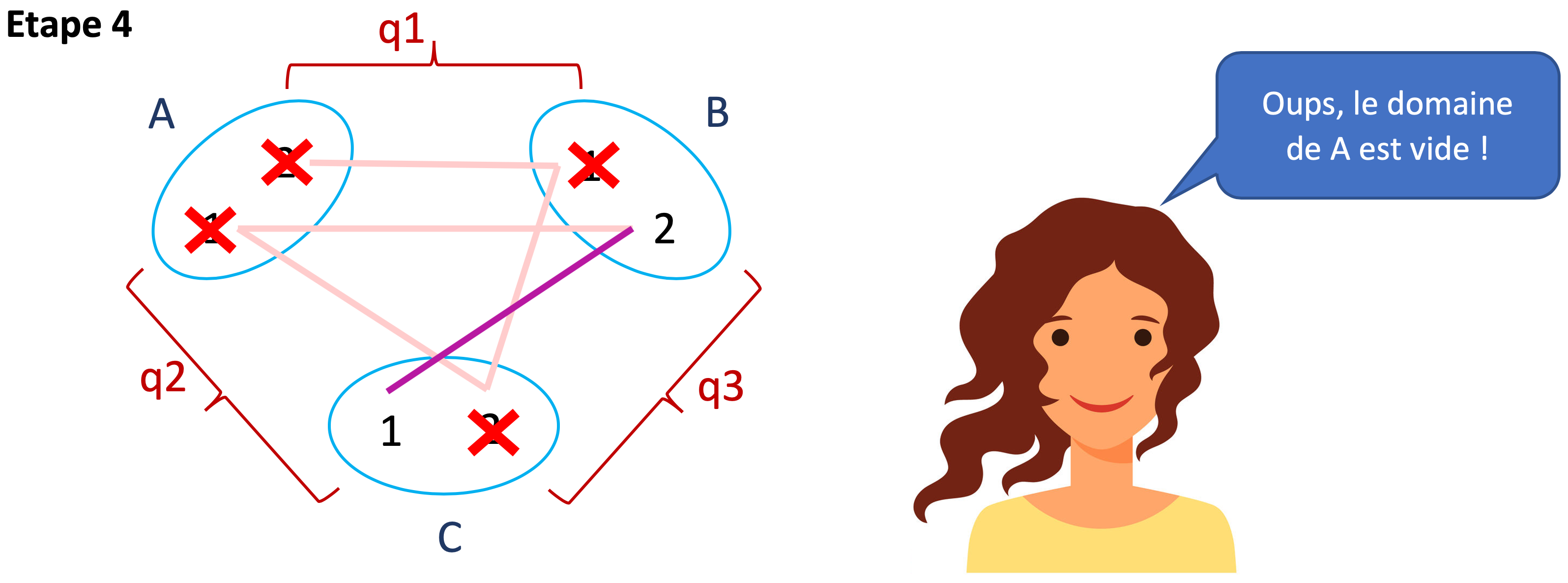
Ici, le filtrage s’est terminé lorsqu’un domaine est devenu vide. Lorsque cela arrive, on peut conclure que le réseau de départ était incohérent. Mais la réciproque n’est pas vraie. Restaurer la cohérence de domaines sur un réseau incohérent n’aboutit pas toujours à vider un domaine. Le filtrage est une simplification d’un réseau de contraintes, mais ne suffit pas toujours à déterminer si ce réseau est incohérent ni à trouver une solution.

Comment restaurer la cohérence de domaines ?

Pour filtrer à la main un réseau de contraintes, il faut « visiter » toutes ses contraintes, une à la fois, puis visiter chaque domaine des variables reliées par cette contrainte, un à la fois, puis visiter chaque valeur du domaine visité et regarder si cette valeur a au moins un support pour la contrainte concernée. Si la réponse est non, on retire la valeur du domaine, sinon on laisse la valeur dans le domaine.

Il est parfois nécessaire de visiter plusieurs fois certaines contraintes et certains domaines car le fait de retirer des valeurs d’un domaine peut faire disparaitre des supports pour des contraintes reliées à la variable concernée, ce qui peut permettre de nouvelles réductions de domaine qui n’étaient pas possibles au départ. On arrête le processus lorsque pour chaque contrainte, toutes les valeurs de tous les domaines des variables concernées ont des supports. La bonne nouvelle, c’est que le résultat est le même quel que soit l’ordre dans lequel on visite les contraintes et les domaines.

Exercices de découverte

C-dec-20

Soit le réseau constitué d’une seule contrainte $A < B$ où les variables $A$ et $B$ ont toutes les deux pour domaine ${1,2,3}$. Restaurez la cohérence de domaine.

"Solution"

C-dec-21

Soit le réseau constitué des deux contraintes $A < B$ et $B < C$ où les variables $A$, $B$ et $C$ ont toutes pour domaine ${1,2,3}$. Restaurez la cohérence de domaine.

"Solution"

Voici trois étapes permettant de réaliser complètement le filtrage.

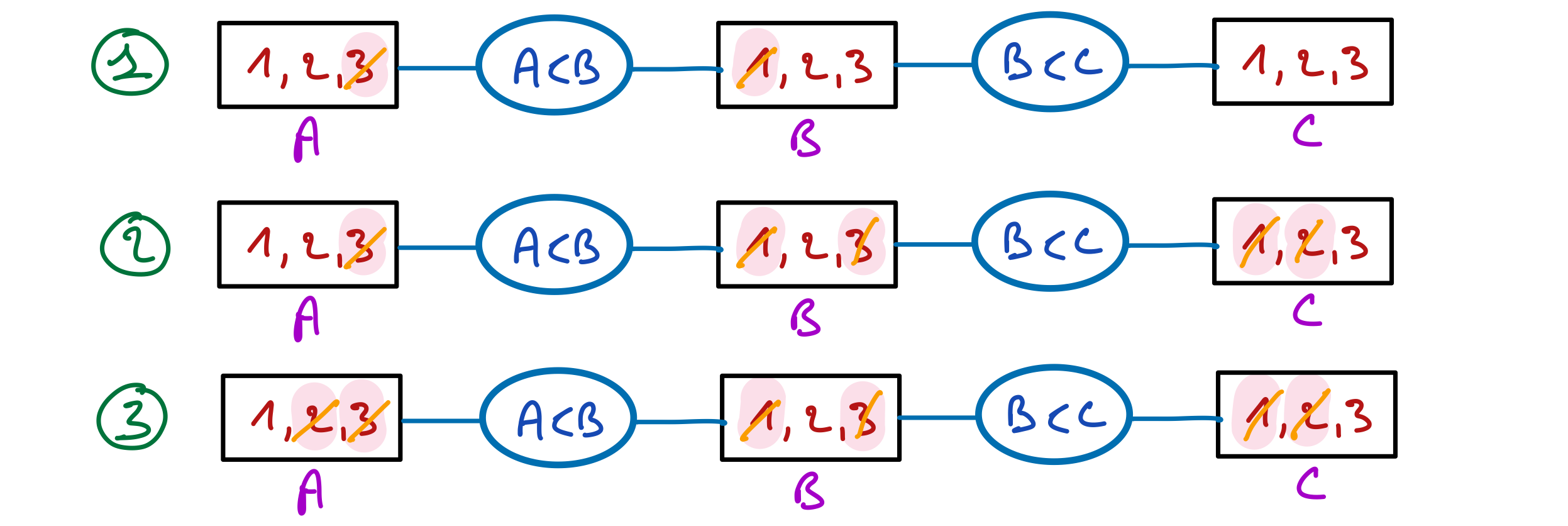
On filtre d’abord la première contrainte exactement comme dans l’exercice précédent. Ensuite on filtre la deuxième, et on constate que le filtrage de la première a retiré le support de $C=2$ qui n’aurait pas été filtré si la contrainte avait été traitée en premier (mais qui aurait fini par être retiré plus tard). Enfin, on revient sur la première contrainte pour constaté que $A=2$ n’a plus de support et doit donc être viré.

C-dec-22

Soit le réseau constitué des trois contraintes $A \neq B$, $B \neq C$ et $A \neq C$ où les variables $A$, $B$ et $C$ ont toutes pour domaine ${1,2}$. Restaurez la cohérence de domaine.

"Solution"

Aucune valeur ne doit être retirée. Le réseau est déjà domaine cohérent. En effet, la restauration de la cohérence de domaine se fait en examinant chaque contrainte séparément. Et si on regarde chaque contrainte séparément, on constante que toutes les valeurs de son domaine ont un support. Évidemment, notre cerveau voit immédiatement qu’il n’y a pas de solution, mais ce n’est pas ce que demande l’énoncé de l’exercice ni ce que ferait un algorithme de restauration de cohérence de domaine.

Rappelez-vous-en le jour de l’examen pour ne pas risquer un hors sujet.

C3 : Quelques algorithmes de restauration de DC- cohérence

Les connaissances présentées dans cette section ne seront pas évaluées.

De nombreux algorithmes de restauration de cohérence de domaines ont été publiés depuis les années 1970. Avant de donner quelques exemples, voici un rappel des notations utilisées pour parler de complexité algorithmique :

Il y a trois notations importantes pour parler de complexité algorithmique :

$f(x) = O(g(x))$ signifie qu’il existe une constante $K$ telle que, au delà d’une certaine valeur de $x$, $f(x)$ est majorée par $K g(x)$.
$f(x) = \Omega(g(x))$ signifie qu’il existe une constante $K$ telle que, au delà d’une certaine valeur de $x$, $f(x)$ est minorée par $K g(x)$.
$f(x) = \Theta(g(x))$ signifie que $f(x) = O(g(x))$ et $f(x) = \Omega(g(x))$.

Dans la suite, nous parlerons de complexité en temps dans le pire des cas des algorithmes présentés. Pour bien comprendre cette notion, vous pouvez vous référer à cette vidéo.

Algorithme naïf AC1

On réitère une procédure de filtrage tant que cette procédure retire au moins une valeur d’au moins un domaine. La procédure est la suivante : pour chaque variable V et chaque contrainte q concernée par V, on retire du domaine de V toutes les valeurs qui n’ont pas de support pour q.

Dans le cas où les contraintes sont binaires (i.e. relient 2 variables) et sont définies en extension, en notant $n$ le nombre de variables, $c$ le nombre de contraintes et $d$ la taille du plus grand domaine, cet algorithme a une complexité temporelle $\Theta(n c d^3)$.

Pourquoi cette complexité ? Il faut jusqu’à $d^2$ itérations pour rechercher toutes les valeurs d’un domaine qui n’ont pas de support pour une contrainte particulière. La procédure de filtrage, qui doit faire cela deux fois par contrainte, a donc une complexité $\Theta(c d^2)$. Comme cette procédure peut n’enlever qu’une seule des $d$ valeurs initiales dans un seul des $n$ domaines, il faut dans certains cas l’appeler $n d$ fois, d’où une complexité en $\Theta(n c d^3)$.

Algorithme AC3 (1977)

On maintient dans un ensemble T les couples (Variable, Contrainte) à traiter. Cet ensemble contient au départ tous les couples (v, q) tels que v est une des variables reliées par q. Tant que cet ensemble n’est pas vide, on réitère les opérations suivantes :

Retirer un couple (v, q) de l’ensemble T.
Filtrer (v, q) en retirant du domaine de v les valeurs non supportées par q.
Si au moins une valeur a été supprimée du domaine de v, alors ajouter dans T tous les couples (u, p) tels que p est une contrainte différente de q, reliant les variables u et v.

Dans le cas d’un réseau de contraintes binaires spécifiées en extension, la complexité temporelle dans le pire des cas d’AC3 est $\Theta(c d^3)$.

Pourquoi cette complexité ? Chaque contrainte est examinée au plus $d$ fois, il y a donc au plus $\text{c~d}$ filtrages de contrainte dont chacun coûte, dans le pire des cas, $\Theta\left( d^{2} \right)$ opérations.

Bref panorama des algorithmes de filtrage pour contraintes binaires

Cette liste d’algorithmes a pour seul vocation de montrer le nombre des contributions et d’améliorations apportées en matière de filtrage de contraintes binaires spécifiées sous forme énumérative : AC4 (1984), AC6(1994), AC7 (1999), AC2001 (2001), AC3d (2002).

AC2001, aussi appelé AC3.1, est une amélioration tardive (21 ans plus tard) de AC3 qui a une complexité temporelle dans le pire des cas $\Theta( c d^{2} )$, et il est impossible de faire mieux. Sa complexité spatiale dans le pire des cas est $\Theta(c d)$.

Cas de la contrainte alldiff

Un algorithme célèbre datant de 1996 (Jean-Charles Regin, [Generalized arc consistency for global cardinality constraint](https://www.researchgate.net/profile/Jean-Charles_Regin/publication/221604096_Generalized_Arc_Consistency_for_Global_Cardinality_Constraint/links/0deec51a6fc6160677000000.pdf, AAAI 96) permet de restaurer la cohérence de domaine sur cette contrainte en temps $\Theta(d^{2} n)$, ou d est la taille du plus grand domaine et n le nombre de variables reliées par la contrainte. Il s’applique à une famille plus générale de contraintes appelées « contraintes globales de cardinalité » et fait appel à des résultats de théorie des graphes relatifs à la notion de flot.

Cas de la contrainte somme

Cette contrainte relie n variables $v_{1},\ \ldots,\ v_{n}$ ayant chacune un domaine contenant des entiers et impose que $v_{1} + \ldots + v_{n} = k$, où k est un entier. On ne connait pas d’algorithme de complexité polynomiale dans le pire des cas pour restauration de la cohérence de domaine sur cette contrainte. Cette contrainte ne peut être filtrée en temps polynomial que si la célèbre hypothèse $P \neq NP$ est fausse.

Exercices d’assimilation

C-ass-00

Restaurez la consistance de domaine sur le réseau de contrainte ci-dessous.

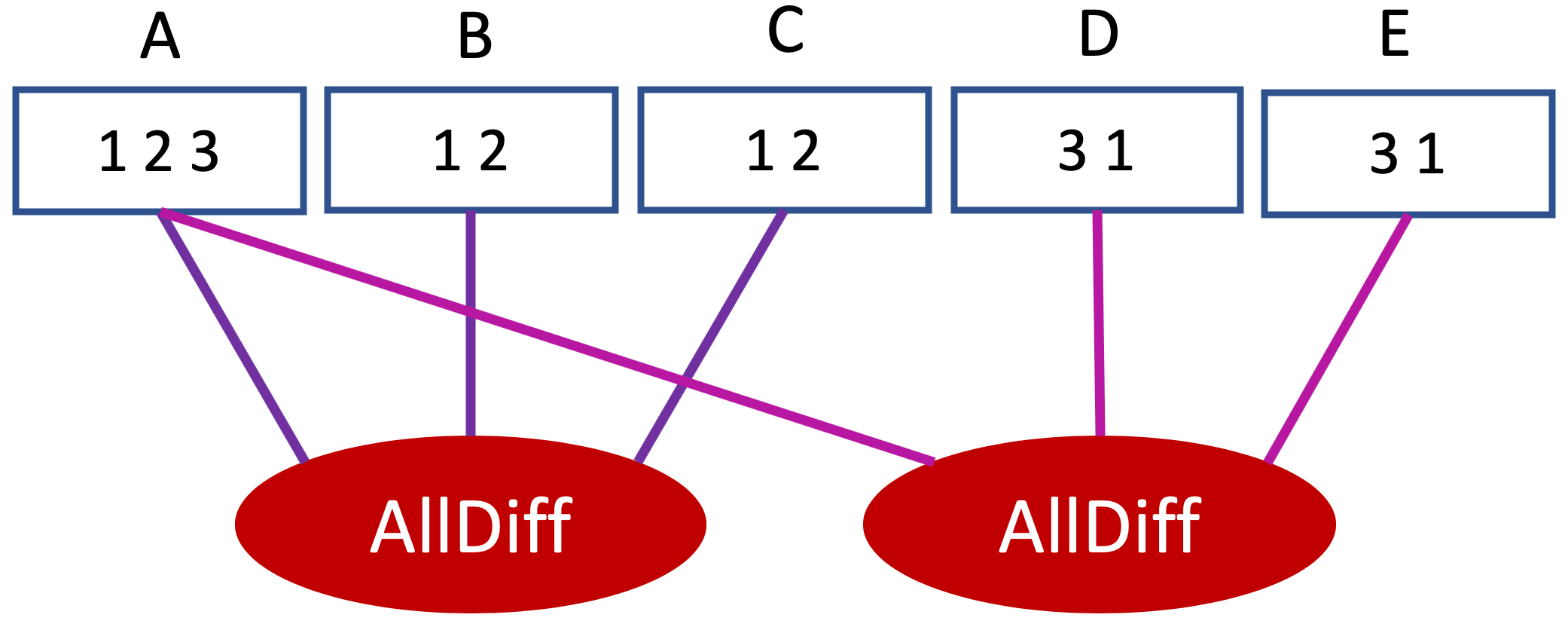
Obtiendrait-on le même résultat en remplaçant les AllDiff par les contraintes binaires $A \neq B,\ A \neq C,B \neq C,\ A \neq D,\ A \neq E,\ D \neq E$ ?

"Indice"

Commençons par la première contrainte (pourquoi pas ?).

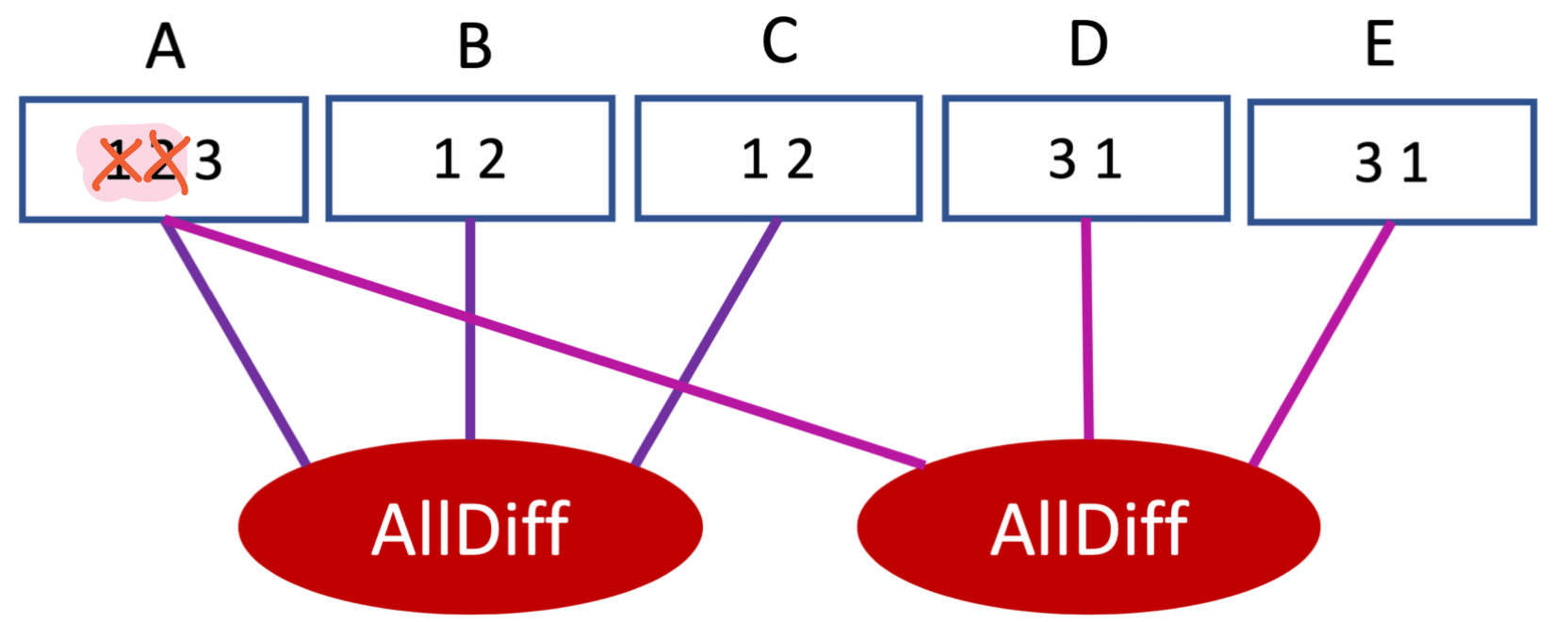
Deux valeurs doivent être retirées A=1 et A=2, parce que si A était assignée avec ces valeurs, il serait impossible de satisfaire alldiff(A, B, C). Il faut maintenant visiter la deuxième contrainte.

"Solution"

Le fait que la seule valeur restante dans le domaine de A soit 3 induit que cette valeur n’est plus utilisable pour D et E. Donc on la retire.

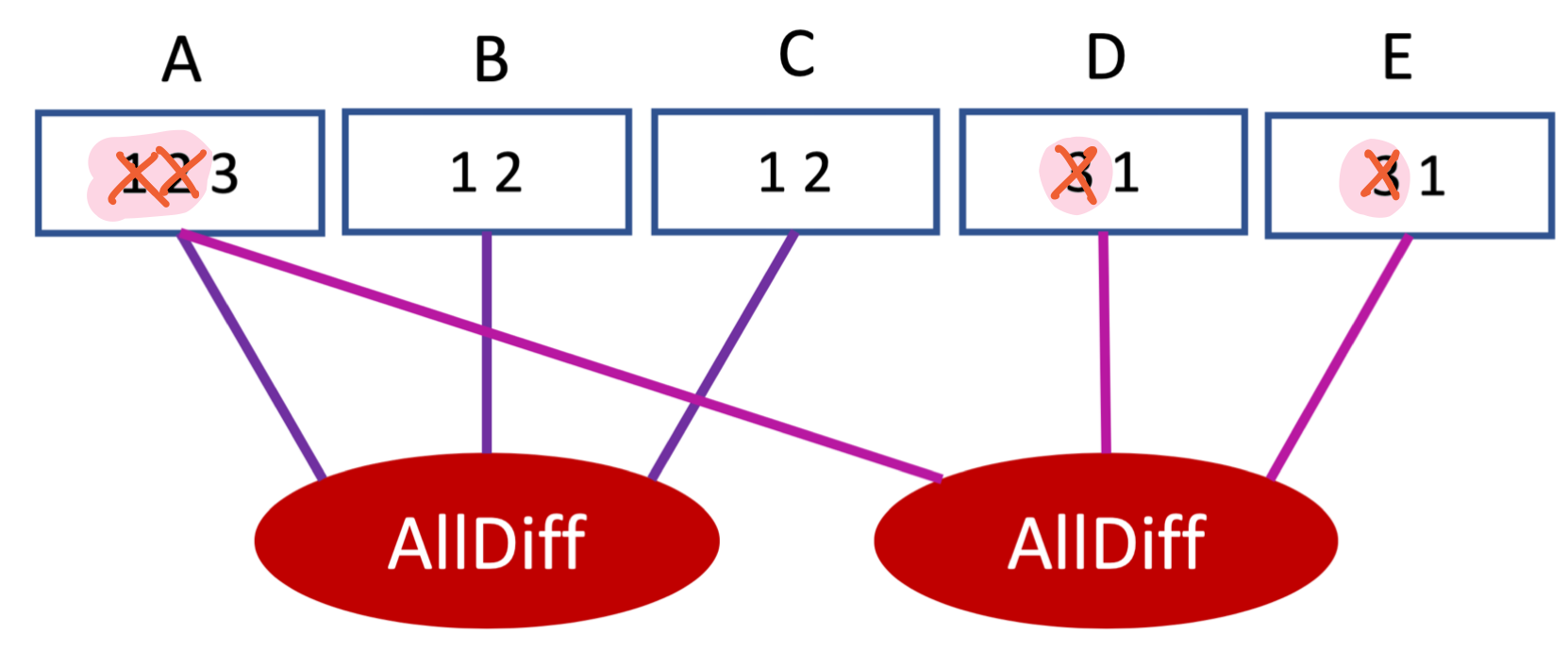
Mais cela induit que D=1, par exemple, n’a plus de support pour la deuxième contrainte. On le retire, ce qui vide complètement le domaine de D.

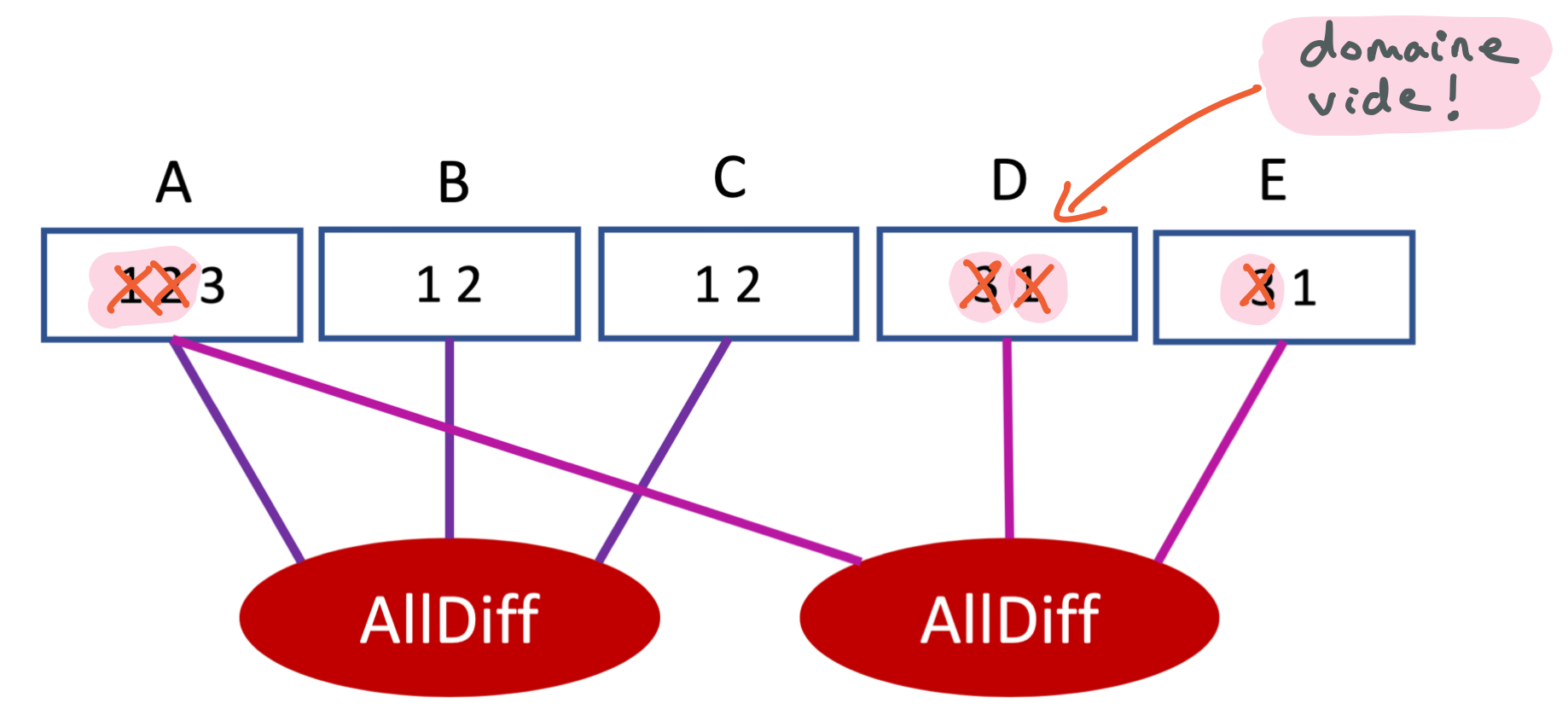
Le filtrage est terminé. Un domaine vide nous permet de conclure que le réseau initial était incohérent.

C-ass02

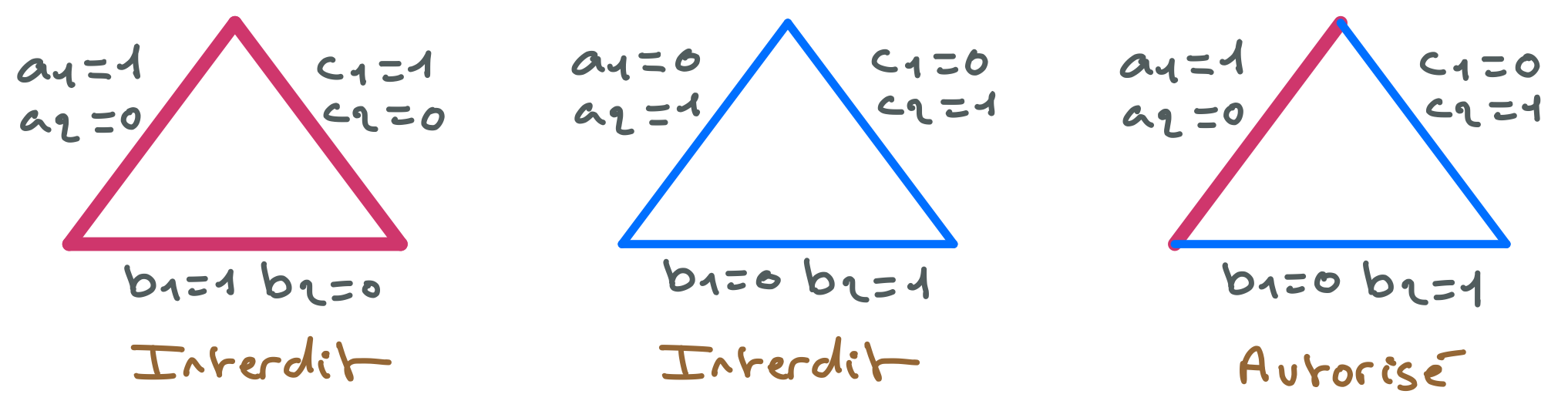
On modélise le problème des 4 reines avec 4 variables A, B, C, D représentant les colonnes d’un échiquier de 4 x 4 et ayant dans leurs domaines les numéros de lignes, {1, 2, 3, 4}. Il y a 6 contraintes binaires exprimées en extension. Par exemple, une des contraintes relie A et B et n’autorise que les valeurs de A et B désignant des positions qui ne sont ni sur la même ligne, ni sur une même diagonale.

Par exemple, $Q_{\text{AB}} = {(1,3),(1,4),(2,4),(3,1),(4,1),(4,2)}$.

Voici quelques exemples de positions de reines qui respectent la contrainte reliant les variables A et B qui concernent les 2 premières colonnes.

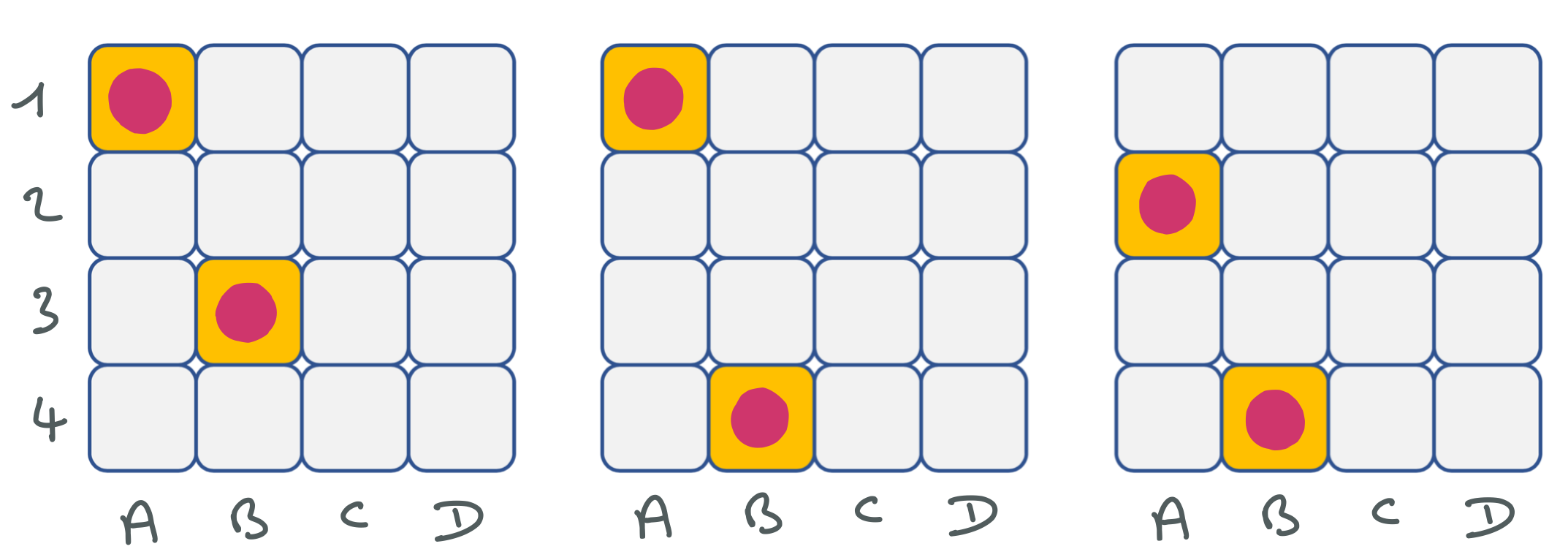
On suppose qu’une reine est déjà en place en position 2 sur la premièrecolonne. Restaurez la cohérence des domaines des trois variables B, C et D en mettant une croix dans les cases correspondant aux valeurs retirées.

"Indice1"

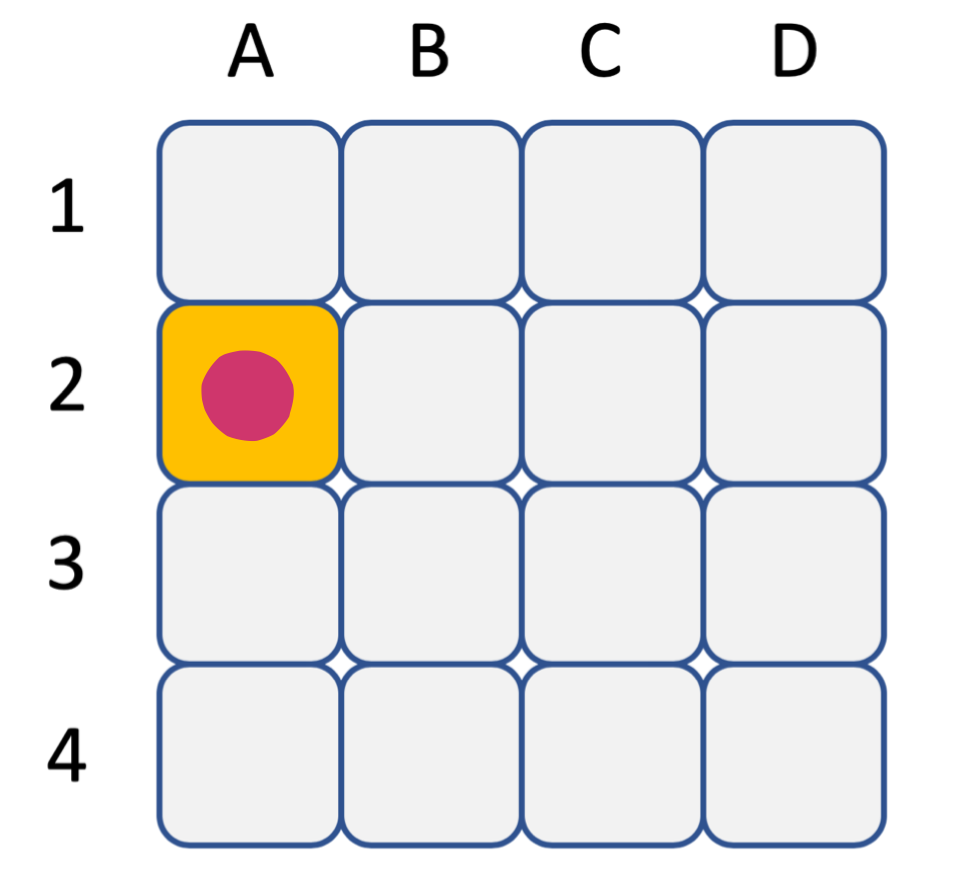
Commençons par la contrainte entre A et B.

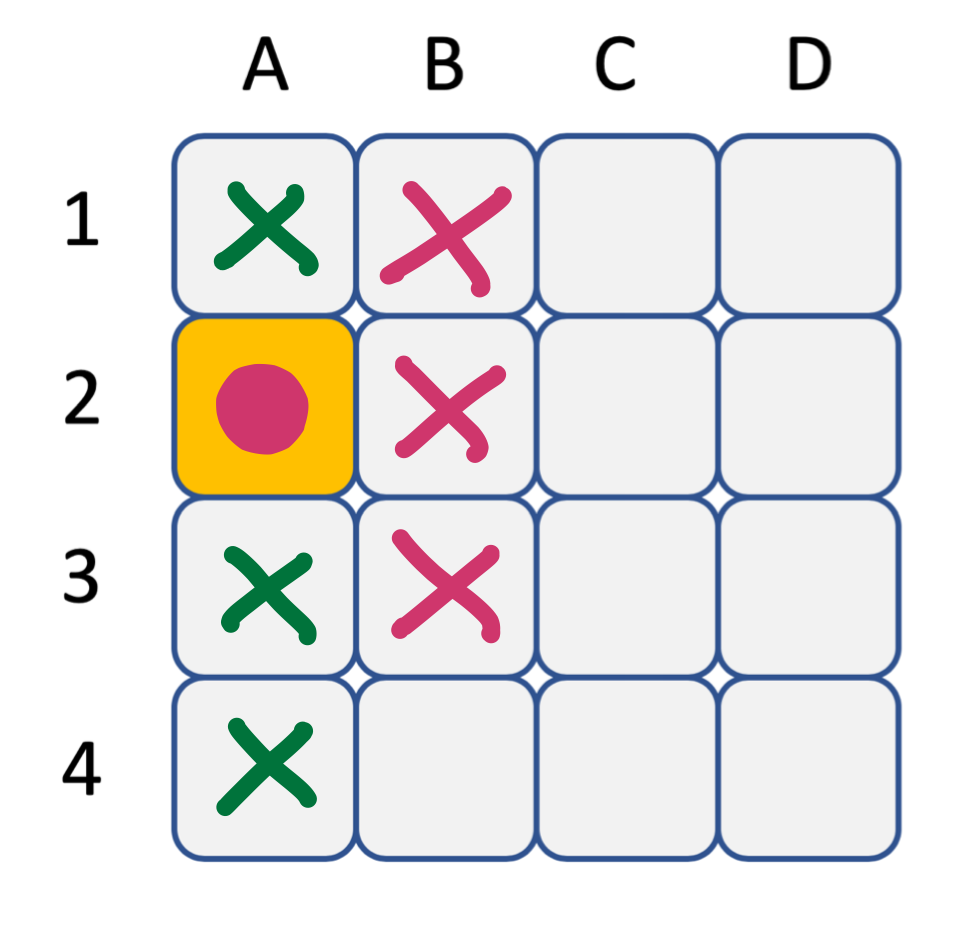A étant assignée à 2, les cases correspondant aux autres valeurs du domaine de A ont été barrées. On voit facilement les valeurs de B qui doivent être retirées. Elles correspondent aux cases menacées par la reine située sur la première colonne. Du coup, il ne reste que 4 dans le domaine de B, ce qui revient à assigner B=4. Pour la suite, merci de visiter la contrainte entre A et C pour que les indices suivants soient pertinents.

"Indice2"

Voici le résultat après filtrage de la contrainte entre A et C et de celle entre A et D.

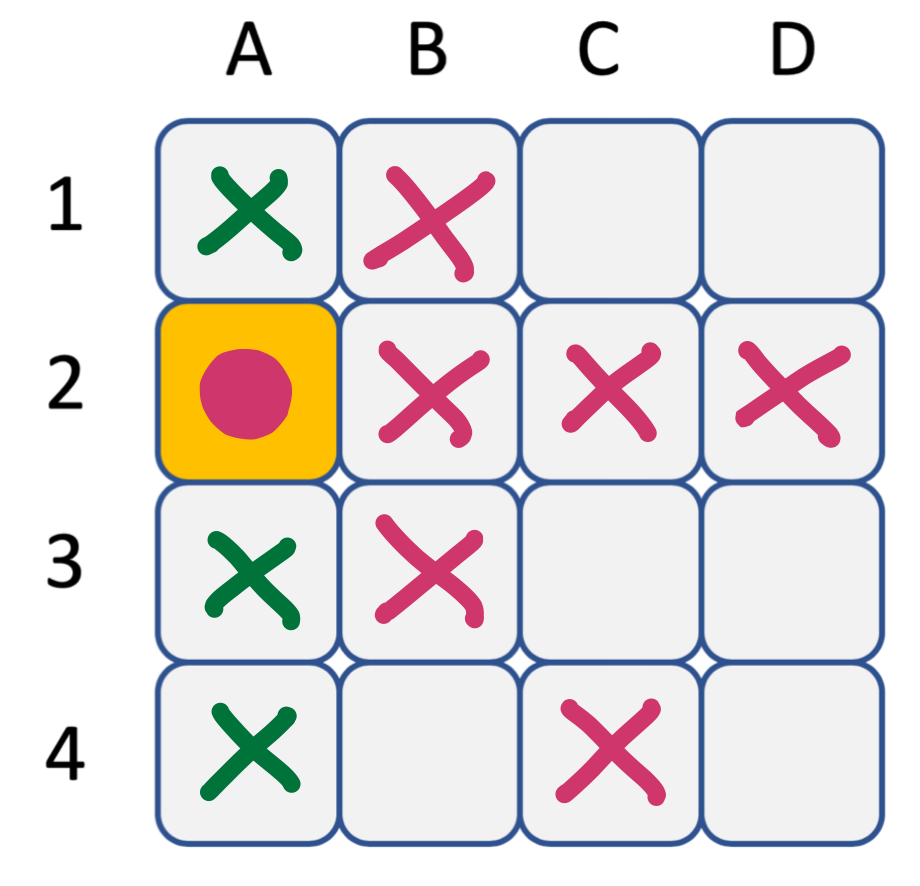
Merci de continuer avec les contraintes entre B et C et entre B et D.

"Indice3"

Voici le résultat du filtrage des contraintes entre B et C et entre B et D.

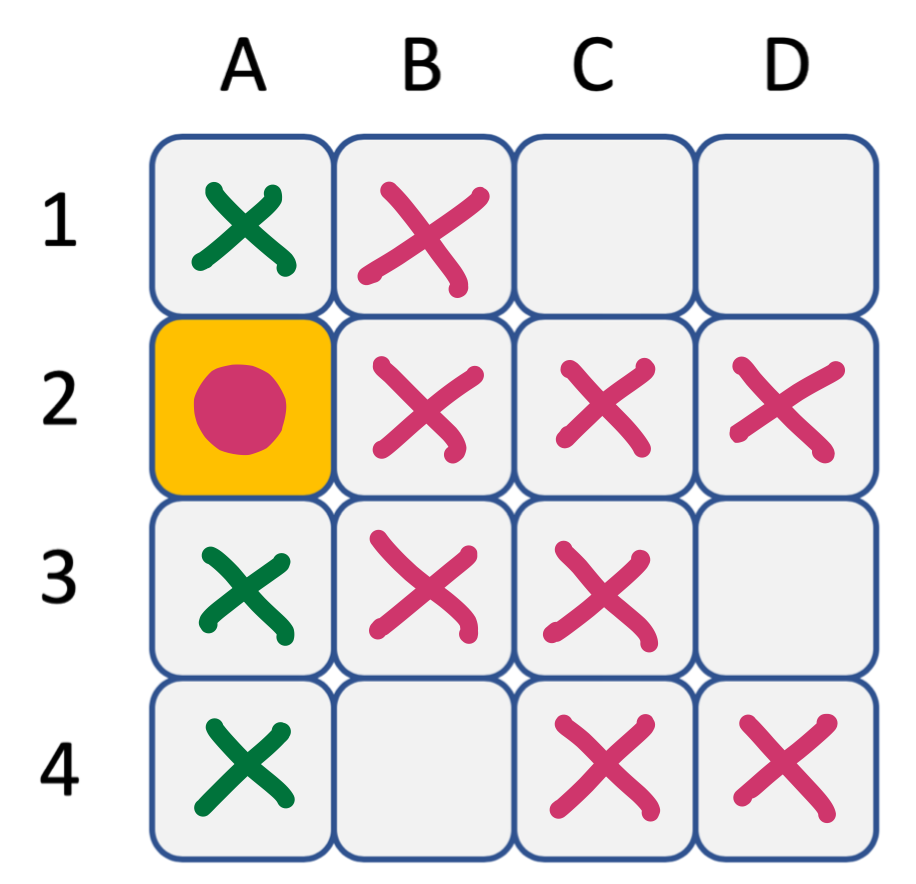
Tentez maintenant de terminer le filtrage.

"Solution"

La valeur D=1 doit être supprimée parce qu’elle n’a plus de support pour la contrainte entre C et D. On arrive à une situation où il ne reste plus qu’une valeur dans chaque domaine, et ces valeurs constituent une solution.

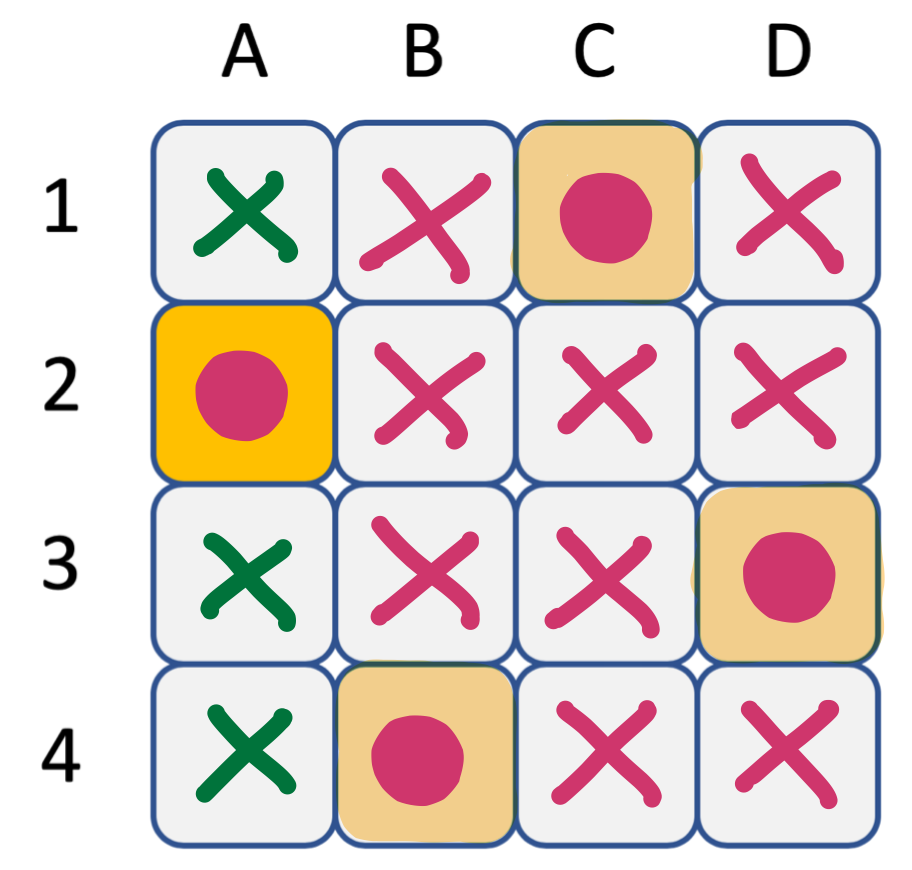
C-ass03

Soit le réseau de contraintes suivant :

Variables : P et L avec domaine 0..8,

Contraintes :

Q1 : P + L = 8
Q2 : P + 2L = 11

Restaurez la cohérence de domaine.

"Indice1"

Il faut commencer par une des contraintes. La première, P + L = 8, ne permet aucun filtrage. Donc on s’intéresse à la deuxième, P + 2L = 11.

On voit assez vite qu’aucune valeur paire de P ne permet de satisfaire P + 2L = 11. Ce qui induit les filtrages suivants dans le domaine de P.

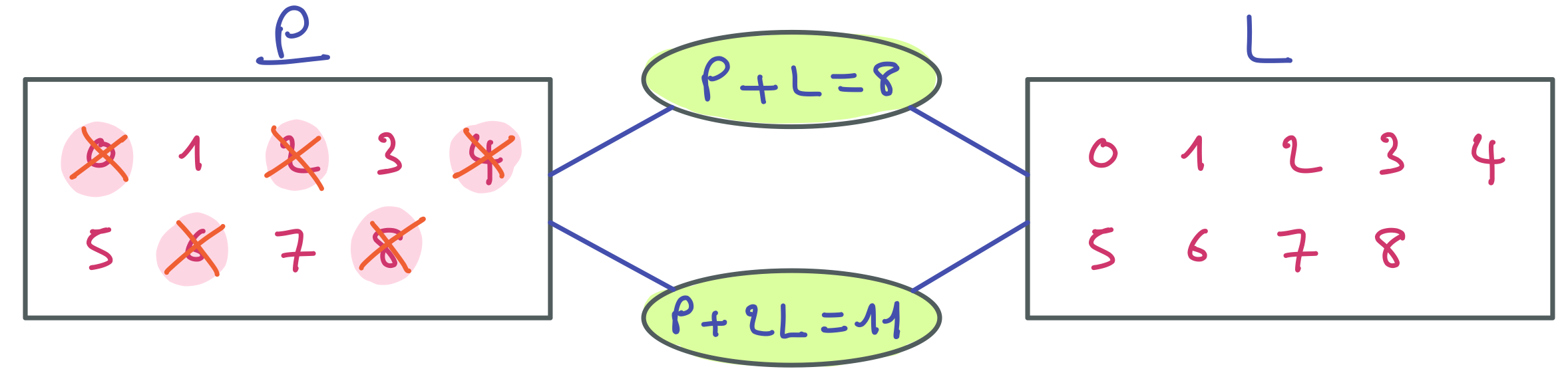
Continuez à filtrer la même contrainte en vous intéressant au domaine de L.

"Indice2"

Voici les valeurs retirées du domaine de L au regard de la contrainte P + 2L = 11.

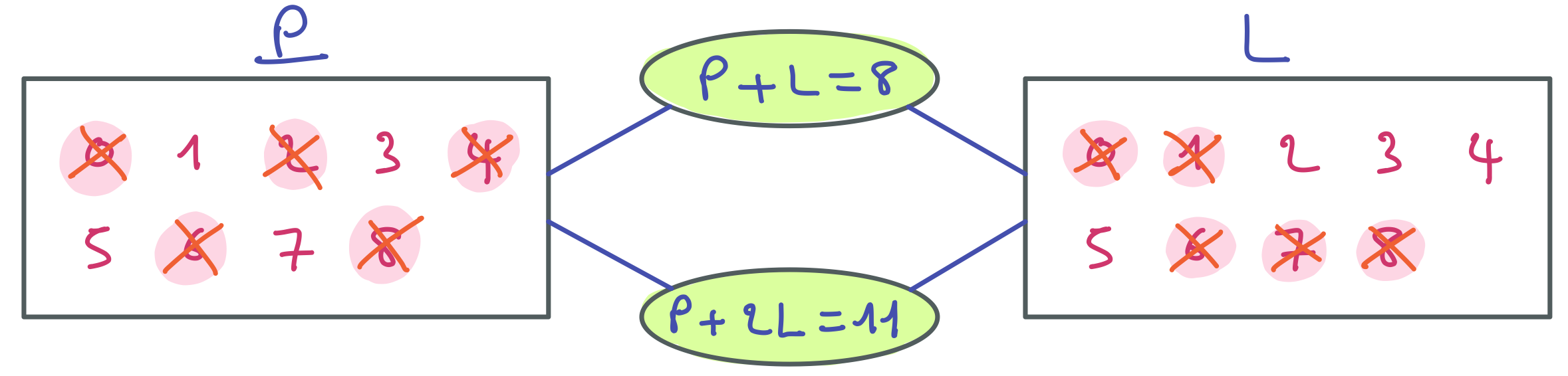
On arrive à un stade où toutes les valeurs des deux domaines ont des supports pour la contrainte P + 2L = 11. Mais le filtrage n’est pas terminé. Intéressez-vous maintenant à la contrainte P + L = 8.

"Indice3"

Voici les valeurs retirées du domaine de P au regard de la contrainte P + L = 8.

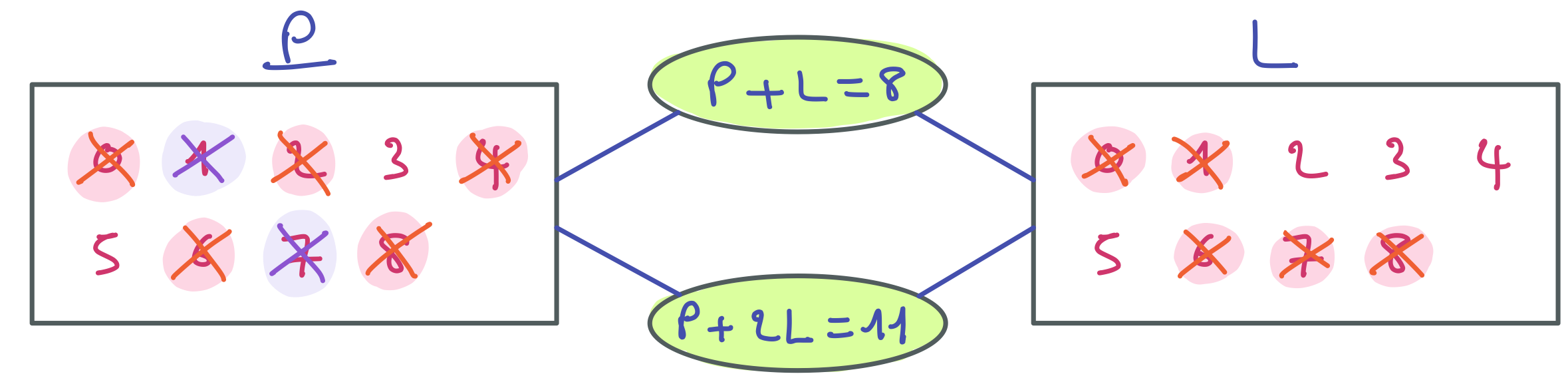
Tentez de continuer le filtrage sur le domaine de L, puis revenez si nécessaire à la contrainte P + 2L = 11.

[spoiler title="Solution"]

On termine le filtrage de la contrainte P + L = 8.

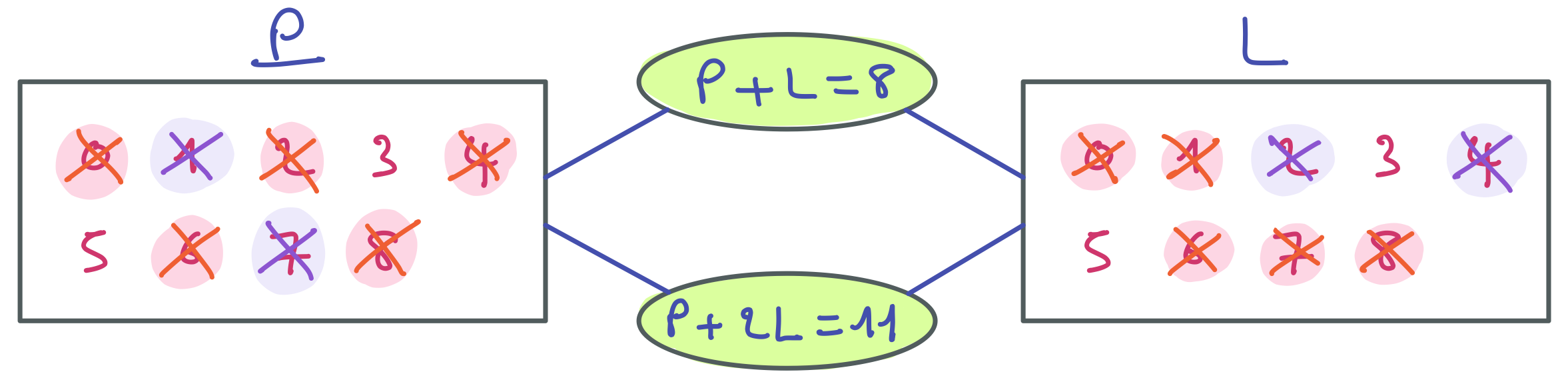
Puis on revient sur la contrainte P + 2L = 11.

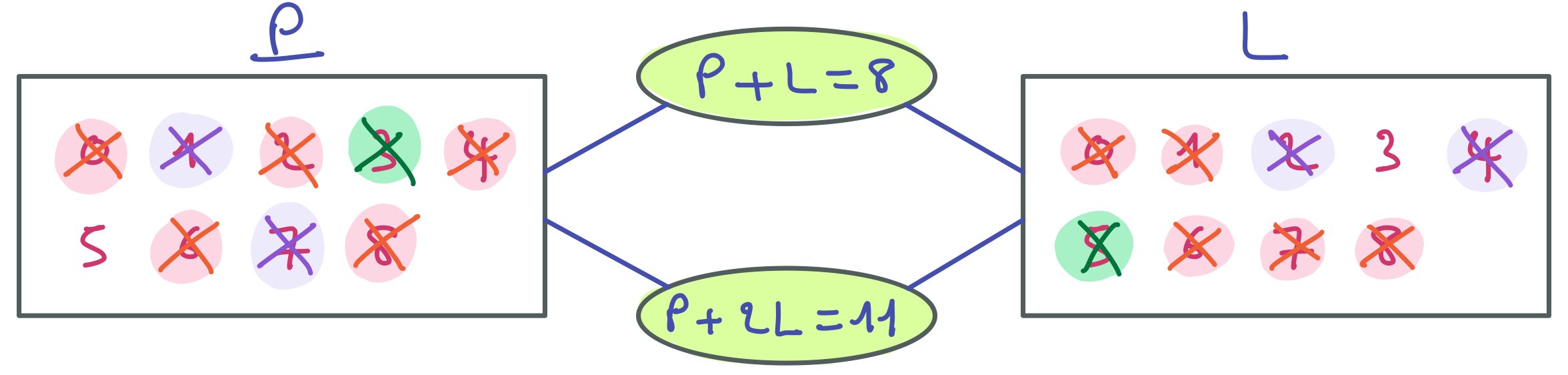
Le filtrage se termine avec une solution. Le problème que vous venez de résoudre est célèbre : Dans une basse-cour, il y a des poules et des lapins. Au total, on compte 8 têtes et 22 pattes. Combien y-a-t-il de poules (P) et de lapins (L) ? La réponse est 5 poules et 3 lapins.

C-ass04

Soit le réseau de contraintes suivant :

Variables : $X_{0},\ X_{1},\ X_{2},\ X_{3}\ \in { 0, 1 }, Y \in { 10,\ 11,\ 14}$

Contrainte : $X_{0} + \ {2X}{1} + \ {4X}{2}, + {\ 8X}_{3} = Y$.

Restaurez la cohérence de domaine.

"Indice"

Il y a une seule contrainte, mais à première vue elle parait difficile à filtrer. Toutefois si on remarque que cette contrainte exprime que les valeurs des variables $X_{0},\ X_{1},\ X_{2},\ X_{3}$ sont les bits de la décomposition en base 2 de l’entier représenté par $Y$, les choses se simplifient. Chaque entier représentable sur 4 bits en base 2 admet une unique représentation en base 2.

Observons les représentations en base 2 des entiers du domaine de la variable $Y$.

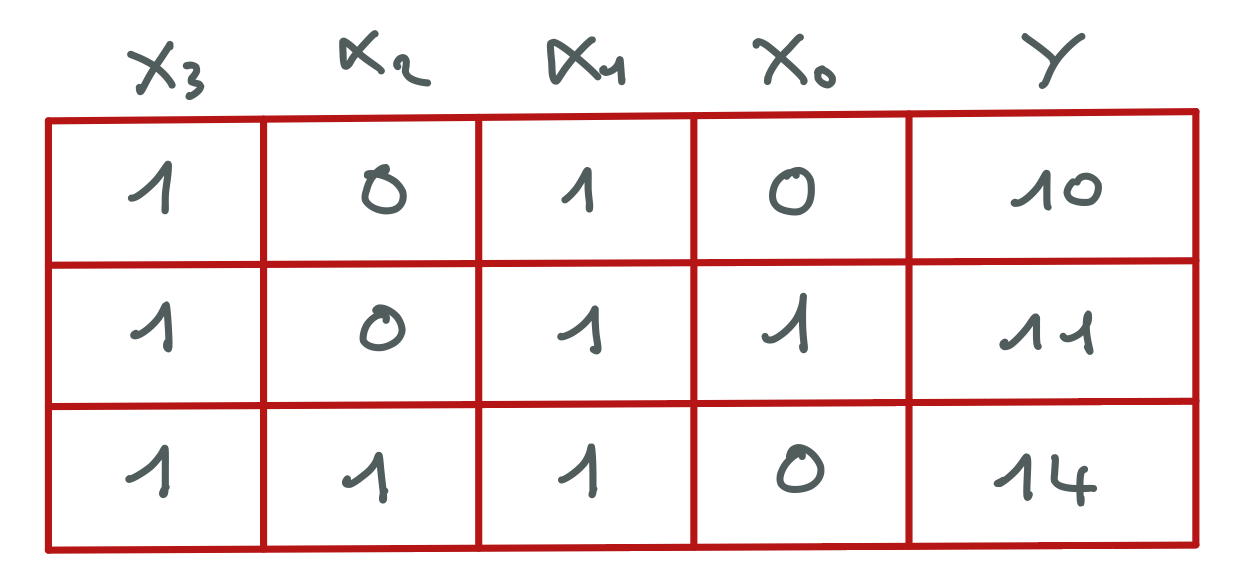
A vous de continuer le raisonnement. On cherche des valeurs des domaines des variables qui, quelles que soient les valeurs des autres variables, ne peuvent permettre de satisfaire la contrainte $X_{0} + \ {2X}{1} + \ {4X}{2}, + {\ 8X}_{3} = Y$.

"Solution"

La table donnée en premier indice peut nous être très utile. Elle nous montre que dans toutes les assignations des variables qui satisfont la contrainte, les valeurs $X_{3} = 0$ et $X_{1} = 0$ n’apparaissent jamais.

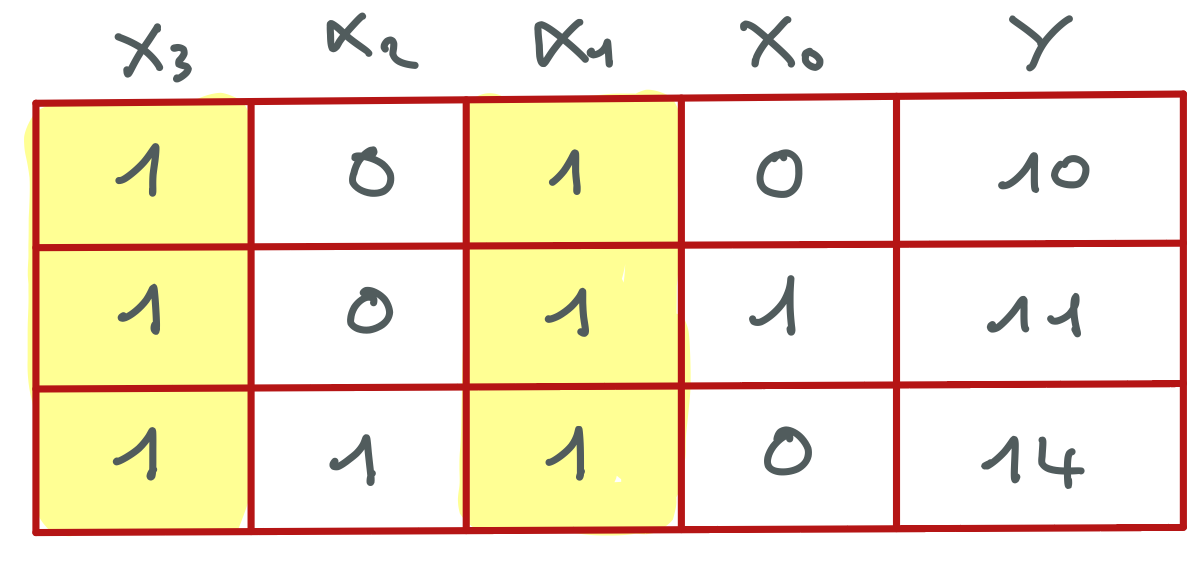
Le résultat du filtrage est :

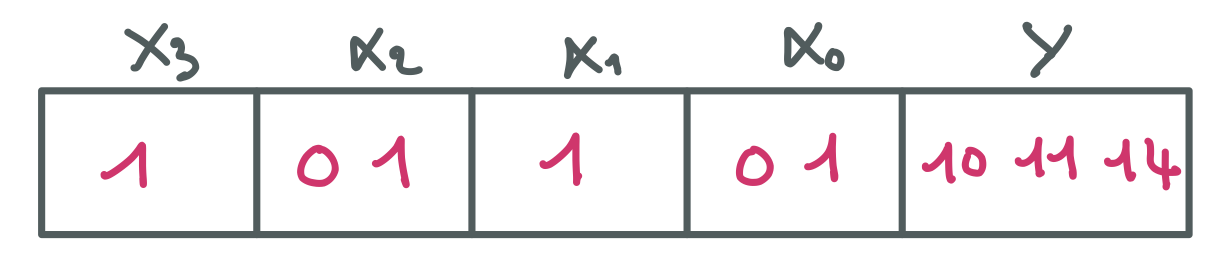
On voit que chaque valeur de chaque domaine apparait dans au moins une des assignations des variables qui satisfont la contrainte, ce qui est précisément ce qui caractérise la cohérence de domaine.

C-ass05

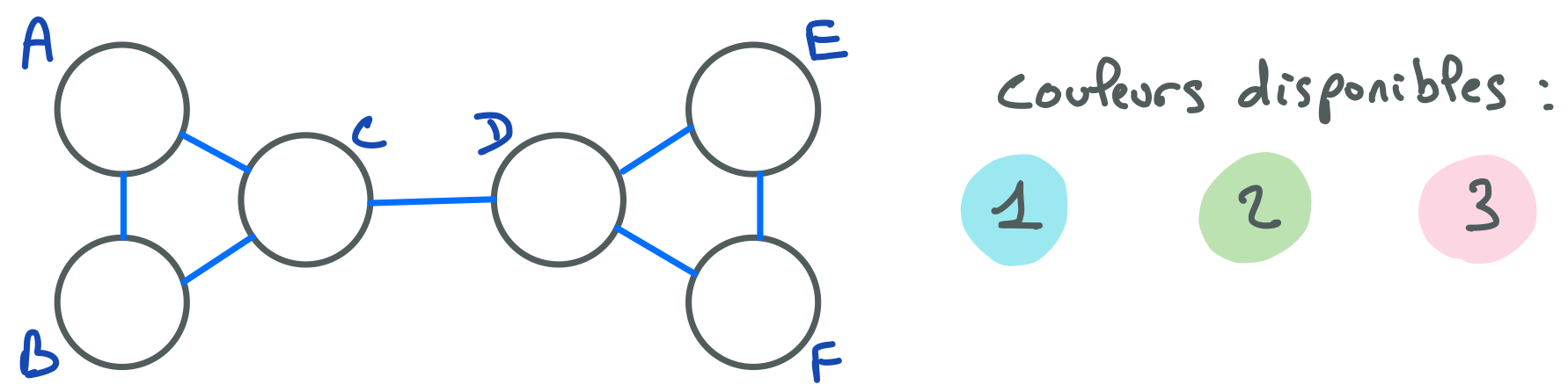
Soit le réseau de contraintes suivant.

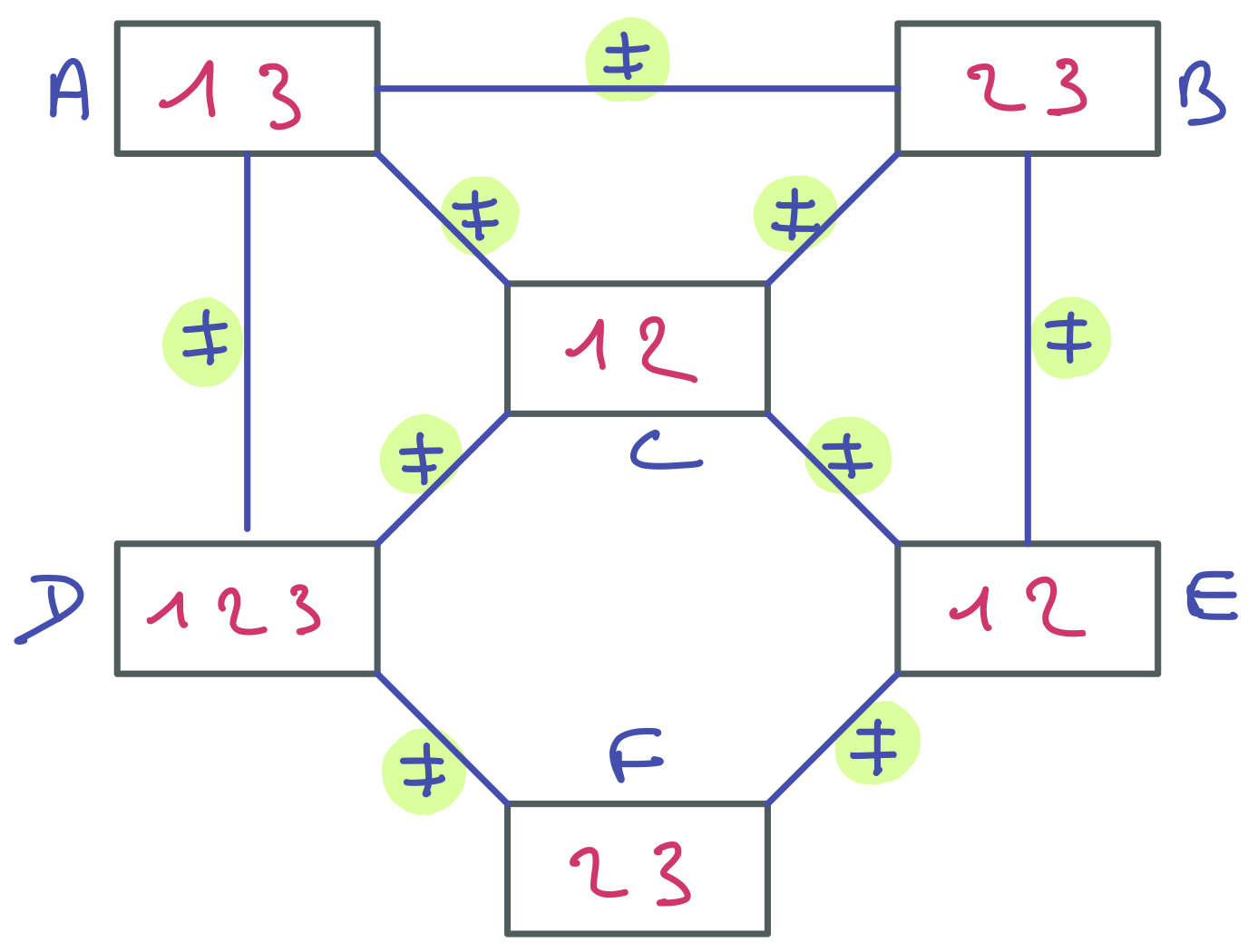
En considérant qu’il y a entre chaque paire de nœuds reliés par une arête une contrainte de différence binaire, restaurez la cohérence de domaine.
Au lieu de modéliser ce problème à l’aide de contraintes binaires, on choisit maintenant d’utiliser une contrainte AllDiff pour chacun des triangles du graphe. Restaurez la cohérence de domaine.

"Indice1"

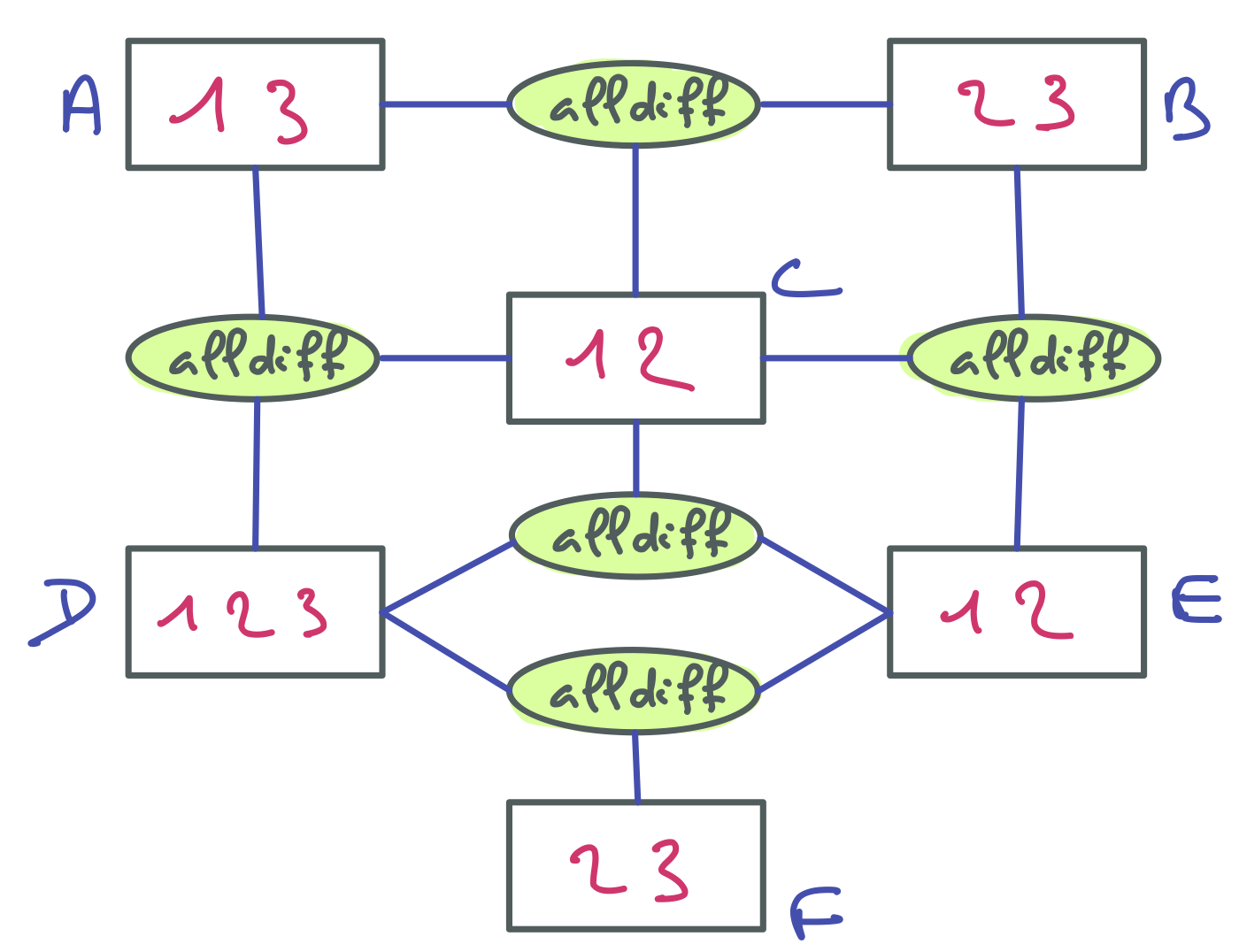
Concernant la première question, la réponse est simple et immédiate. On ne peut filtrer une contrainte binaire de différence que si l’un des domaines concernés est un singleton dont l’élément est dans l’autre domaine, comme par exemple {2} et {2, 5}. Si les deux domaines ont plus d’un élément, chaque valeur a nécessairement un support.

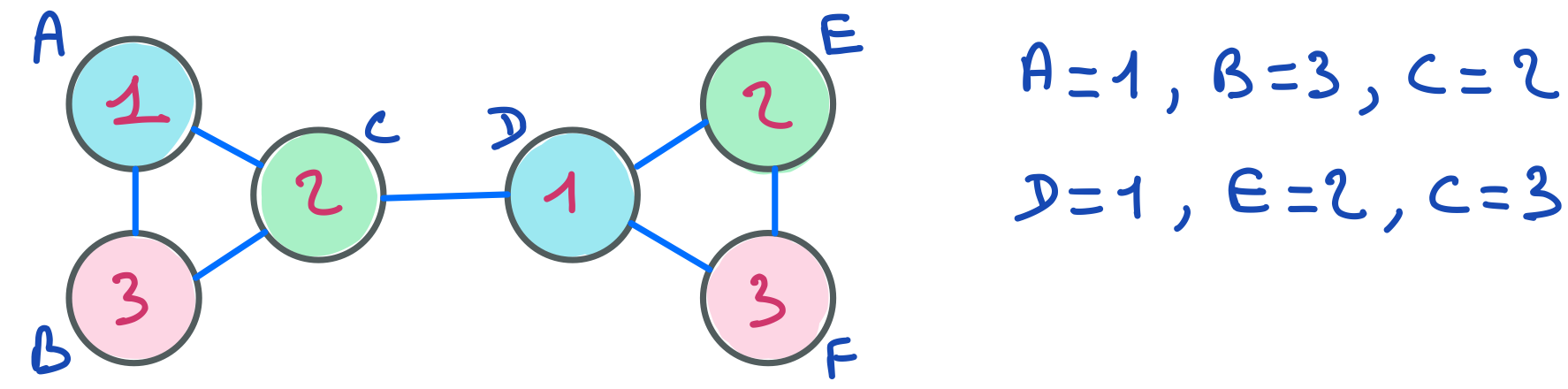
Par contre, des filtrages sont possibles avec la version spécifiée à l’aide de contraintes alldiff.

"Indice2"

Il faut trouver une première contrainte qui filtre. Par exemple celle-ci.

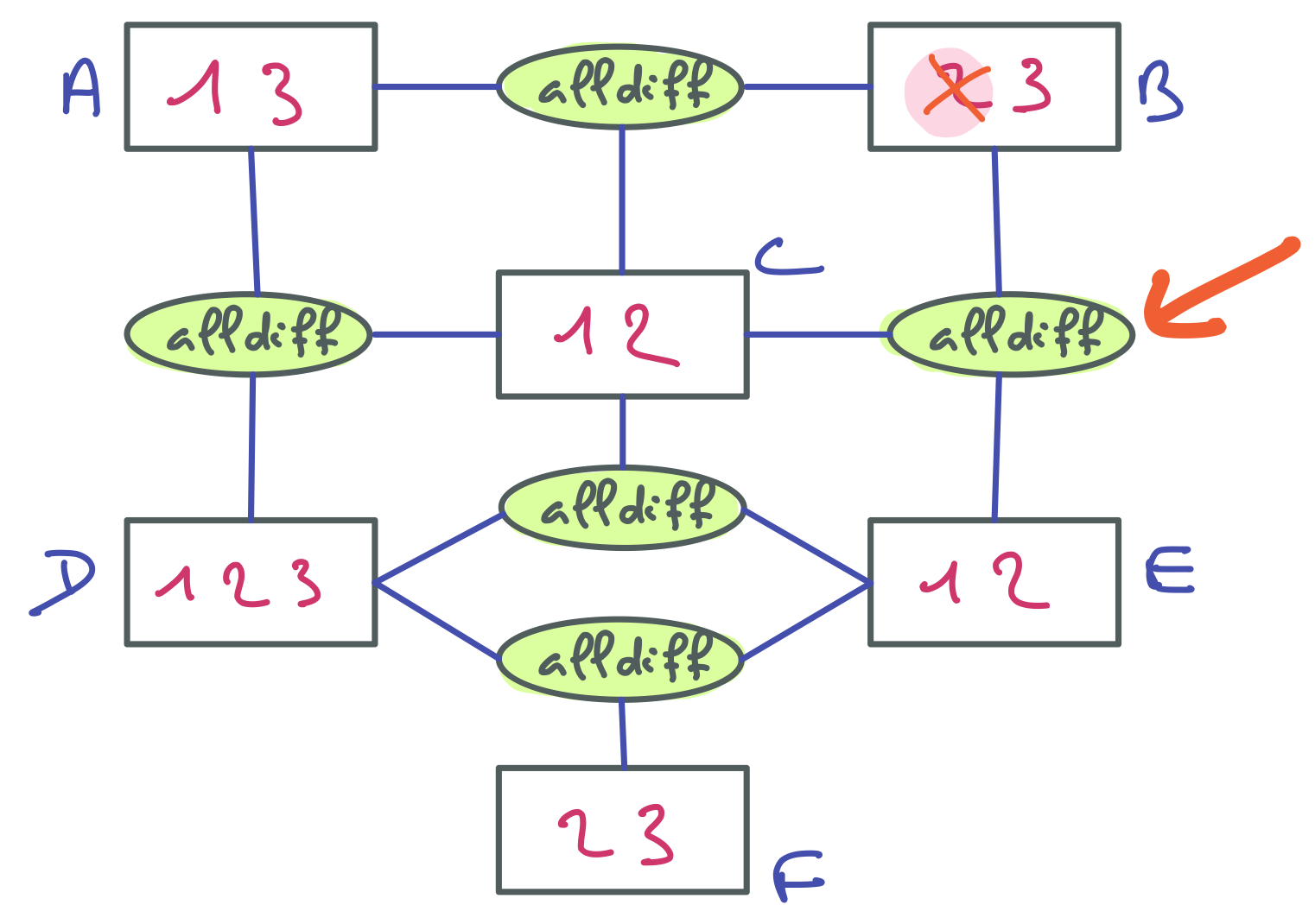
La suppression de B=3 va entrainer d’autres filtrages. A vous de les trouver.

"Solution"

En visitant successivement les contraintes, on arrive rapidement à cette solution.

Programmation par contraintes : partie B

Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Partie B : Modélisation d’un problème

Objectif

Être capable de modéliser sous la forme d’un réseau de contraintes un problème combinatoire à vérifiabilité polynomiale exprimé en langage naturel et /ou en langage mathématique.

Prérequis

Partie A.

Introduction

La modélisation est une activité de conception, donc une activité créative, comme c’est le cas de l’invention d’un algorithme qui résout un problème, bien que ce ne soit pas du tout la même chose. Modéliser un problème à l’aide de contraintes est donc tout autant un art qu’une technique. Il n’existe pas de recette et c’est surtout la pratique, l’expérience, qui vous rendra apte à traiter de nouveaux problèmes. Il y a tout de même une démarche intellectuelle que je vais illustrer par un exemple.

Il faut déjà bien comprendre que qu’on attend de vous lorsqu’on vous demande de modéliser un problème, et en particulier que vous devez livrer un réseau de contraintes, c’est-à-dire :

des variables,
des domaines,
et des contraintes !

B1 : Un exemple

Nous allons modéliser pas à pas le problème du sac à dos. Voici son énoncé.

L’énoncé du problème

On dispose d’un sac à dos dans lequel on souhaite placer des objets à sélectionner parmi une liste de N d’objets. Chaque objet de la liste a un poids (en Kilogrammes) et une valeur (en Euro) et peut être ou non sélectionné pour être placé dans le sac. Le nombre d’objets placés dans le sac n’est pas limité, mais la somme de leurs poids ne doit pas excéder W, et la somme de leur valeur doit être au moins égale à V.

Une instance de problème est donc définie par une liste de poids $w_{1},\ldots w_{N}$, une liste de prix $v_{1},\ldots v_{N}$, une charge maximale $W$ et une valeur minimale $V$.

Bien comprendre ce qui est attendu

Une des choses essentielles à bien comprendre est que dans l’énoncé du problème, il n’y pas de variables. N, $w_{1},\ldots w_{N}$, $v_{1},\ldots v_{N}$, W et V sont, à l’échelle d’une instance du problème, des constantes. Ce sont des données parfaitement connues au moment de résoudre le problème.

Le solveur qui va résoudre le problème ne doit pas décider quel poids ou quelle valeur a chaque objet, ni la capacité du sac, ni la valeur minimum à transporter. Tous cela est déjà connu au moment de résoudre le problème.

Ce que le solveur doit décider, c’est quels objets mettre dans le sac et lesquels ne pas mettre dans le sac. Et c’est cela que les valeurs des variables doivent nous dire dans une solution du problème qui sera, si applicable, trouvée par le solveur.

Il faut donc que toute solution puisse être représentée par une assignation des variables qui nous dise, pour chaque objet, s’il va aller ou non dans le sac.

Les variables

Un réseau de contraintes s’articule autour de variables. Il faut donc commencer par proposer des variables dont les assignations sont susceptibles de représenter une solution.

Puisque, dans une solution, chaque objet a deux états possibles : pris ou pas pris, on peut modéliser le problème à l’aide de N variables $X_{1},\ldots,X_{n}$ à domaine {0,1}.

On donne un sens aux assignations : $X_{i} = 1$ signifie que l’objet $i$, (de poids $w_{i}$ et de valeur $v_{i}$) est dans le sac. Bien sûr, $X_{i} = 0$ signifie qu’il n’est pas dans le sac.

Voici une assignation qui représente une solution de notre exemple d’instance.

Ce choix de variables à domaines ${ 0,1}$ sera un bon choix si on arrive à exprimer les contraintes qui traduisent les exigences exprimées dans l’énoncé du problème.

Les contraintes

Nous avons donc choisi d’utiliser N variables Booléennes pour modéliser une instance du problème du sac à dos avec N objets. Il nous reste à trouver les contraintes qui spécifient si une assignation particulière de ces variables est une solution.

Or, d’après l’énoncé, il y a deux propriétés à vérifier :

La somme des poids des objets mis dans le sac ne doit pas dépasser W.
La somme des valeurs des objets mis dans le sac doit être au moins égale à V.

On peut exprimer ces propriétés sous la forme de deux contraintes arithmétiques sur les variables :

$$Q1\ :\sum_{i = 1}^{N}{w_{i}X_{i}}\ \leq W$$

$$Q2\ :\sum_{i = 1}^{N}{v_{i}X_{i}}\ \geq V$$

En effet, on voit facilement que pour une assignation particulière des variables, $\sum_{i = 1}^{N}{w_{i}X_{i}}$ représente la somme des poids des objets qui sont dans le sac, et que $\sum_{i = 1}^{N}{v_{i}X_{i}}$ représente la valeur totale de ces objets.

Les contraintes Q1 et Q2 sont appelée contraintes arithmétiques linéaires. Examinons le réseau de contraintes obtenu avec notre instance d’exemple.

Variables : $X_{1},X_{2},X_{3},X_{4},X_{5}$ avec domaines {0,1}

Contraintes :

Q1 : $0.05 X_{1} + 1.2 X_{2} + 0.9 X_{3} + 0.1X_{4} + 0.9X_{5} \leq 2$
Q2 : $5.9 X_{1} + 749 X_{2} + 5 X_{3} + 0.5 X_{4} + 79 X_{5} \geq 755$

Le problème est modélisé. Cet exemple nous a juste donné une idée de la démarche de modélisation, mais les choix des variables, des domaines, et la spécification des contraintes sont font au cas par cas et nécessitent une certaine créativité et un peu d’expérience.

Exercices de découverte

B-dec-10

Donnez des critères simples permettant d’identifier facilement certaines instances du problème n’ayant aucune solution.

"Solution"

Si la somme des valeurs de tous les objets est inférieure à $V$ ou si l’objet le plus léger a un poids supérieur à $W$ alors on peut conclure immédiatement que le problème n’a pas de solution.

Exercices d’assimilation

Pour acquérir une première expérience de la modélisation en programmation par contraintes, il n’y a pas trente-six mille moyens. Il faut faire traiter des exemples divers et variés, en prenant le temps de réfléchir à chaque cas. L’erreur fatale serait de regarder trop vite les solutions des exercices d’entraînement qui vont vous être proposés. C’est comme si vous tentiez d’apprendre à jouer du piano juste en observant un pianiste en action.

B-ass-00

Aguirre, Brunissendre, Clodomir et Déothéria travaillent dans une entreprise où 4 machines doivent être exploitées. Chaque machine requiert une personne qualifiée, et une personne ne peut s’occuper que d’une seule machine. Voici les compétences des Employés.

	Personnes compétentes
Machine 1	Aguirre, Brunissendre, Clodomir, Déothéria
Machine 2	Aguirre, Brunissendre, Clodomir, Déothéria
Machine 3	Clodomir, Déothéria
Machine 4	Déothéria

On ne vous demande pas une solution, mais un réseau de contraintes dont des solutions représentent des solutions de cette instance de problème. Votre modélisation doit être généralisable à toute autre instance de ce problème avec un nombre quelconque de personnes et autant de machines.

La première question que vous devez vous poser est : quelles variables et quels domaines ? Nous avons 4 personnes et 4 machines. Réfléchissez d’abord aux possibilités avant de lire la suite.

"Indice

On pourrait utiliser 4 variables, chacune associée à une personne. Ces variables pourraient être nommées A, B, C, D pour Aguirre, Brunissendre, Clodomir et Déothéria.

"Indice

Si le domaine d’une variable associée à une personne est l’ensemble des numéros des machines sur lesquelles cette personne est habilitée à travailler, alors toute assignation des variables revient à attribuer à chaque personne une machine qu’elle peut gérer. Et ceci sans avoir encore écrit la moindre contrainte.

Variables :

$A$ avec domaine {1, 2}
$B$ avec domaine {1, 2}
$C$ avec domaine {1, 2, 3}
$D$ avec domaine {1, 2, 3, 4}

Mais alors, la modélisation est terminée ? En fait non. S’il n’y a aucune contrainte, toutes les assignations sont des solutions, y compris par exemple ${ A = 1,\ B = 1,\ C = 1,\ D = 1}$. Voyez-vous ce qui cloche ? La modélisation recherchée doit non seulement permettre d’assigner une machine à chaque personne, mais elle doit aussi faire en sorte que toutes les machines soient assignées et qu’une même personne ne puisse être assignée à plusieurs machines. Pour exprimer cela, il nous faut des contraintes. Essayez de trouver lesquelles.

"Solution"

On peut simplement exprimer que chacune des variables doit avoir une valeur différente des autres. Ainsi, deux personnes ne peuvent pas travailler sur une même machine, et donc les 4 machines sont occupées.

Contraintes :

$A \neq B$, $A \neq C$,$\text{\ A} \neq B,$ $A \neq D$, $B \neq C$, $B \neq D$, $C \neq D$.

Il existe une contrainte particulière qui exprime cela de manière plus concise : $\mathbf{\text{alldiff}}(A,B,C,D)$. Cette contrainte se généralise à un nombre quelconque de variables et est satisfaite, comme son nom l’indique, si et seulement si les valeurs des variables reliées sont toutes différentes. Il n’y a rien d’autre à ajouter, notre problème est modélisé.

Cette modélisation fonctionne aussi s’il y a plus d’employés que de machines. Elle garantit alors que toutes les machines sont utilisées (si la distribution des compétences le permet) et qu’une et une seule machine est assignée à chaque personne.

B-ass-01

Soit le réseau de contraintes suivant.

Variables :

A et B avec domaine {1,2}
C avec domaine {1,2,3}

Contrainte :

AllDiff(A,B,C)

Donnez une spécification en extension de la contrainte.

"Indice

Cet exercice est très facile. La seule difficulté est de comprendre l’énoncé. La contrainte est spécifiée ici en compréhension. On demande une reformulation en extension, c’est-à-dire par énumération des assignations des variables A, B, C qui satisfont cette contrainte. La présentation est condensée sous la forme d’un ensemble de triplets.

Sur A, B, C : {…}

"Indice

Comme ce réseau ne comporte qu’une seule contrainte, la représentation en extension de cette contrainte revient à donner les solutions du réseau.

"Solution"

Sur A, B, C : {(1, 2, 3), (2, 1, 3)}

B-ass-02

Proposez une modélisation du problème des sacs à dos. Ce problème est une généralisation du problème du sac à dos que nous avons modélisé précédemment dans laquelle on N objets ayant chacun un poids et une valeur, mais avec K sacs ayant chacun la même charge maximale W.

Chaque objet peut être placé dans au plus un sac, et la somme des valeurs de tous les objets emportés (placés dans un sac) doit être au moins égale à une valeur V donnée.

"Indice

Il faut bien sûr relire la description de la modélisation du problème avec un seul sac à dos, dans lequel, pour chaque objet, une variable Booléenne indique s’il est ou non dans le sac. Ici, on a plusieurs sacs, et pour chaque objet $i$ et chaque sac $j$, soit l’objet $i$ est dans le sac $j$, soit il n’y est pas. Il est de fait tout à fait possible que certains objets ne soient dans aucun sacs.

"Indice

On a N objets pouvant chacun être dans un des K sac ou dans aucun sac. Une première idée pourrait être d’associer à chaque objet $i$ une variable $Y_{i}$ de domaine ${ 0,\ 1,\ \ldots,\ K}$ avec le sens suivant : $Y_{i} = 0$ si l’objet $i$ n’est dans aucun sac, et $Y_{i} = j$, pour $j \in 1..K$, si l’objet $i$ est dans le sac $j$.

Cette idée n’est pas du tout mauvaise à priori. Elle serait même plutôt bonne si on envisageait d’écrire un algorithme pour résoudre le problème. Mais ce n’est pas du tout le cas. On cherche une modélisation avec des contraintes qui spécifie le problème et non un algorithme qui le résout. Or avec ce choix de variables, comment écririez-vous les contraintes relatives aux poids et valeurs des objets embarqués ? Ce serait lourd et difficile. Il est beaucoup plus facile de travailler uniquement avec des variables Booléennes.

"Indice

On définit $NK$ variables $X_{\text{ij}},\ i \in 1..N,\ j \in 1..K$ à domaines {0,1}. Le sens des assignations de ces variables est le suivant : $X_{\text{ij}} = 1$ indique que l’objet $i$ est dans le sac $j$, $X_{\text{ij}} = 0$ indique que l’objet $i$ n’est pas dans le sac $j$. Il vous reste à écrire les contraintes.

"Indice

Pour exprimer que le coût total des objets embarqués est au moins égal à $V$, on écrit :

$$\Sigma_{i = 1}^{N}\Sigma_{j = 1}^{K}{v_{i}X}_{\text{ij}} \geq V$$

Prenez le temps de bien comprendre cette contrainte. S’il vous faut 10 minutes, prenez 10 minutes ; s’il vous faut 20 minutes, prenez-en 20. Vous n’êtes pas obligé de tout comprendre instantanément, mais si vous brulez les étapes sans vraiment comprendre en profondeur les solutions, vous ne progresserez pas. Pour bien comprendre pourquoi on fait la somme de toutes les variables multipliées par les valeurs des objets associés, prenons un exemple avec 4 objets et 2 sacs. On sait que chaque objet doit être dans au plus un sac, ce qui devra être spécifié par d’autres contraintes que celle qui nous intéresse ici. Imaginons une assignation qui respecte cette condition comme par exemple celle illustrée ci-dessous.

Maintenant, reprenons la matrice des variables en multipliant les valeurs assignées aux variables (0 ou 1) par les prix des objets concernés. Nous obtenons ceci :

La somme des termes représente bien le cumul des prix des objets embarqués. La prochaine étape consiste à trouver les contraintes qui expriment que la charge maximale de chaque sac n’est pas dépassée. Il vous faudra donc spécifier une contrainte par sac.

"Indice

On pose une contrainte de charge pour chaque sac. La contrainte de charge pour le sac $j$ est :

$$\Sigma_{i = 1}^{N}w_{i}X_{\text{ij}} \leq W$$

Si on reprend notre petit exemple avec la même assignation, chaque contrainte relie les variables d’une même ligne correspondant à un sac $j$ et le terme $\Sigma_{i = 1}^{N}w_{i}X_{\text{ij}}$ représente le cumul des poids des objets qui sont dans ce sac.

Mais ce n’est pas terminé. Il manque encore des contraintes. Jusqu’à maintenant, nous avons considéré comme implicite qu’un objet ne peut être placé dans plusieurs sac. Mais il faut spécifier cette interdiction par des contraintes. Sans cela, un solveur à qui on demanderait de résoudre notre problème pourrait nous trouver des solutions qui satisfont toutes les contraintes mais dans lesquelles certains objets seraient présents dans plusieurs sacs. À vous de trouver les contraintes manquantes.

"Solution"

On doit ajouter une nouvelle contrainte pour chaque objet, spécifiant que cet objet peut se trouver dans au plus un sac. Pour chaque objet $i$, on peut écrire :

$$\Sigma_{j = 1}^{k}X_{\text{ij}} \leq 1$$

Ce qui « autorise » l’objet à être présent dans aucun sac ou dans un seul sac.

B-ass-03

Dans le cadre de cet exercice, on appelle contrainte arithmétique linéaire normalisée une contrainte de la forme $a_{1}x_{1} + … + a_{n}x_{n} \leq b$, où $a_{1},\ .\ .\ .,\ a_{n},\ b$ sont des entiers relatifs (i.e. positifs, négatifs ou nuls) et $x_{1},\ .\ .\ .\ ,\ x_{n}$ des variables à domaine {0, 1}.

Soient $y_{1},\ y_{2},\ y_{3}$ des variables à domaine {0, 1}. Modélisez à l’aide d’une ou plusieurs contraintes arithmétiques linéaires normalisées chacune des propriétés suivantes :

au moins une des variables $y_{1},\ y_{2},\ y_{3}$ a la valeur 1;
aucune des variables $y_{1},\ y_{2},\ y_{3}$ n’a la valeur 1;
toutes les variables $y_{1},\ y_{2},\ y_{3}$ ont la valeur 1;
au moins une des variables $y_{1},\ y_{2},\ y_{3}$ a la valeur 0.

"Indice

Commençons par une contrainte facile à spécifier telle que la numéro 2. Aucune des variables n’a la valeur 1, ça signifie qu’elles ont toutes la valeur 0. On peut alors écrire :

$y_{1} + y_{2} + y_{3} \leq 0$

On pourrait remplacer le $\leq$ par $=$, mais nous devons respecter la forme exacte $a_{1}x_{1} + \ … + \ a_{n}x_{n}\ \leq \ b$ imposée par l’énoncé.

"Indice

Passons à la contrainte numéro 4. Au moins une des variables a la valeur 0. Cela suppose que leur somme ne peut atteindre la valeur 3. On peut donc écrire :

$y_{1} + y_{2} + y_{3} \leq 2$

"Indice

Passons à la contrainte numéro 3. Comment dire que toutes les variables ont la valeur 1 ? Cela revient à dire que leur somme vaut 3. Pour l’exprimer avec $\leq$, on peut écrire :

$- y_{1} – y_{2} – y_{3} \leq – 3$

On utilise des coefficients -1 pour les variables et une valeur $b = – 1$, ce qui est autorisé par l’énoncé, contrairement aux opérateurs de comparaison $=$ ou $\geq$.

"Solution"

Il reste une dernière contrainte, la numéro 2, qui dit qu’au moins une des variables doit avoir la valeur 1. La somme des variables doit donc être au moins égale à 1. En changeant les signes, on a :

$- y_{1} – y_{2} – y_{3} \leq – 1$

B-ass-04

Soient les variables a1, a2, b1, b2, c1, c2 à domaine {0,1} représentant les couleurs des trois arêtes d’un triangle avec la convention suivante : a1=1 (respectivement b1=1, c1=1) signifie que l’arête A (respectivement B, C) est rouge, a2=1 (respectivement b2=1, c2=1) signifie que l’arête A (respectivement B, C) est bleue.

Donnez une spécification en compréhension de toutes les contraintes nécessaires pour spécifier que la coloration est cohérente, i.e. chaque arête a exactement une couleur, et que le triangle n’est pas monochrome, i.e. que les arêtes ne sont pas toutes de la même couleur.

"Indice"

Commençons par la cohérence des coloriages. On doit avoir $a_{1} \neq a_{2}$, $b_{1} \neq b_{2}$, $c_{1} \neq c_{2}$. Mais on pourrait l’exprimer différemment, par exemple $a_{1} + a_{2} = 1$ etc.

"Solution"

Il faut à présent spécifier que le triangle ne doit pas être monochrome. La contrainte $a_{1} + b_{1} + c_{1} \neq 3$ empêche le triangle d’être complètement rouge. La contrainte $a_{2} + b_{2} + c_{2} \neq 3$ l’empêche d’être complètement bleu. Ces deux contraintes sont suffisantes, mais il y a d’autres manières d’exprimer la même chose.

B-ass-05

On appelle $\text{conv}(X,\ \ B_{0},\ \ B_{1},\ \ldots,B_{n – 1})$ la contrainte reliant une variable $X$ de domaine $0..2^{n – 1}$ et $n$ variables $B_{0}, \ldots,B_{n – 1}$ de domaines {0,1} qui est satisfaite si et seulement si les valeurs $B_{0}, \ldots,B_{n – 1}$ représentent les bits de la représentation de $X$ en base 2. Par exemple, l’assignation $X = 12, B_{3} = 1, B_{2} = 1, B_{1} = 0, B_{0} = 0$ satisfait la contrainte $\text{conv}(X, B_{0}, B_{1}, B_{2}, B_{3})$ parce que 12 a pour représentation 1 1 0 0 en base 2.

Donnez une spécification en compréhension de $\text{conv}(X, B_{0}, B_{1}, B_{2}, B_{3})$ en utilisant exclusivement des opérateurs arithmétiques +, *, = et des constantes.

Donnez une spécification énumérative de $\text{conv}(X, B_{0}, B_{1})$.

En utilisant la contrainte conv et des contraintes arithmétiques de votre choix (limitées aux opérateurs +, =, <), proposez une modélisation du problème suivant : Trouver un entier X compris entre 5 et 9 (inclus) dont la représentation en base 2 comporte exactement 3 bits ayant la valeur 1.

"Indice

Il faut commencer par donner comme contrainte la formule qui exprime la décomposition d’un entier en base 2 :

$$X = \ B_{0} + \ 2B_{1} + 4B_{2} + 8B_{3}$$

"Indice

Pour la spécification en compréhension, il faut bien comprendre que ce qui est attendu est la liste de toutes les assignations des variables $X,\ B_{0},\ B_{1}$ qui satisfont la contrainte :

Sur $X,\ B_{0},\ B_{1}$, ${(0,0,0),\ (1,1,0),\ (2,0,1),\ (3,1,1)}$.

"Indice

Nous abordons la dernière question de l’exercice, on cherche à spécifier qu’un certain entier $X$ est compris entre 5 et 9, ce qui peut s’écrire en introduisant une variable $X$ de domaine {5, 6, 7, 8, 9}. Aucune contrainte n’est nécessaire. Par contre, pour exprimer que la représentation de X en base 2 comporte 3 bits à 1, on doit introduire 4 variables supplémentaires, $B_{0},\ B_{1},\ B_{2},\ B_{3}$ avec domaines {0, 1}. Essayez de continuer seul avant de consulter l’indice suivant.

"Solution"

Nous avons donc actuellement le réseau suivant :

Variables :

$X$ avec domaine {5, 6, 7, 8, 9}
$B_{0}, B_{1}, B_{2},B_{3}$ avec domaine {0, 1}

Il nous manque les contraintes :

Contraintes :

$\text{conv}(X, B_{0}, B_{1}, B_{2}, B_{3})$
$B_{0} + B_{1} + B_{2} + B_{3} = 3$

B-ass-06

On appelle règle toute suite strictement croissante d’entiers commençant par la valeur 0. Chacun de ces entiers est appelé une marque. On dit qu’un entier d est une distance mesurable par une règle si et seulement s’il existe deux marques a, b de cette règle (non nécessairement consécutives) telles que b − a = d. Par exemple, les distances mesurables par la règle ⟨ 0, 1, 3, 6 ⟩ sont les valeurs 1, 2, 3, 5 et 6. La longueur d’une règle est la valeur de sa dernière marque (c’est donc aussi la plus grande distance mesurable avec cette règle).

On appelle règle de Golomb toute règle dont chaque distance mesurable ne peut être mesurée que d’une seule manière possible. Par exemple, la règle ⟨ 0, 1, 3, 6 ⟩ n’est pas une règle de Golomb car elle permet de mesurer la distance 3 de deux manières différentes : soit en utilisant les marques 0 et 3, soit en utilisant les marques 3 et 6. En revanche, ⟨ 0, 1, 4, 6 ⟩ est une règle de Golomb ayant pour distances mesurables les valeurs 1, 2, 3, 4, 5 et 6. Vous pouvez vériﬁer qu’il n’y a bien qu’une seule paire de marques permettant de mesurer directement chacune de ces distances.

On souhaite déterminer s’il existe une règle de Golomb de longueur n avec k marques. Proposez une modélisation sous la forme d’un problème de satisfaction de contraintes, en précisant (en fonctions des valeurs n et k) quelles sont les variables, leurs domaines, et les contraintes qui les relient.

"Indice

D’abord les variables. La règle recherchée possède k marques qui peuvent être représentées par des variables $X_{0},\ \ldots X_{k – 1}.$ Par convention, la première marque vaut 0 et la dernière représente la longueur de la règle. Les autres ont des valeurs comprises entre 1 et $n – 1$. Donc :

Variables :

$X_{0}$ avec domaine {0}
$X_{k – 1}$ avec domaine {n}
$X_{1}$ à $X_{k – 2}$ avec domaines 1..n-1.

"Indice

On peut introduire de nombreuses contraintes pour dire que toute distance entre deux graduations est différente de toute autre.

Pour tout $i,\ j,\ k,\ m$, tels que $(i,j) \neq (k,m),\ i < j,\ k < m$, on ajoute la contrainte :

$$X_{j} – X_{i} \neq X_{m} – X_{k}$$

Par exemple pour 5 marques (k=5) on aurait 90 contraintes, dont certaines redondantes. Même en spécifiant un peu plus finement les contraintes, on en aura toujours $O(n^{4})$, ce qui n’est pas « interdit », mais guère satisfaisant. On peut limiter le nombre de contraintes en introduisant des variables supplémentaires associées aux distances.

Pour tout $i \in 0..(k – 2),\ j \in (i + 1)\text{..}(k – 1)$, on introduit une variable $D_{\text{ij}}$ de domaine $1..n$. On doit alors spécifier deux types de contraintes :

des contraintes qui expriment que chaque variable $D_{\text{ij}}$ représente la distance entre les marques $i$ et $j$,
et des contraintes qui expriment que les variables $D_{\text{ij}}$ ont des valeurs toutes différentes.

"Solution"

Nous avons donc les variables suivantes :

$X_{0}$ avec domaine {0}
$X_{k – 1}$ avec domaine {n}
$X_{1}$ à $X_{k – 2}$ avec domaines 1..n-1
$D_{\text{ij}},\ i \in 0..k – 2,\ j \in (i + 1)\text{..}(k – 1)$ avec domaines $1..n$

Les contraintes à ajouter sont les suivantes :

$D_{\text{ij}} = X_{j} – X_{i}$, $i \in 0..(k – 2),\ j \in (i + 1)\text{..}(k – 1)$
alldiff$\left( { D_{\text{ij}},\ i \in 0..(k – 2),\ j \in (i + 1)\text{..}(k – 1)} \right)$

La contrainte alldiff relie toutes les variables de distance.

Voici un schéma du réseau obtenu avec $k = 4$ :

B-ass-07

On dispose de N salles numérotée de 1 à $N$. Ces salles disposent chacune d’équipements de différents types en quantité variable. Il y a $M$ types d’équipements possibles, numérotés de 1 à $M$. Les quantités des différents types d’équipements disponibles dans les salles sont représentés par des constantes notées $E_{\text{jk}}$. $E_{\text{jk}} = r$ signifie que la salle $j$ dispose de $r$ ressource de type $k$.

On souhaite assigner $P$ personnes, numérotées de 1 à $P$, à ces salles. Une salle peut accueillir une ou plusieurs personnes à condition de disposer des équipements dont elles ont besoin. Les équipements dont ont besoin les personnes sont représentés par des constantes notée $B_{\text{ik}}$. $B_{\text{ik}} = r$ signifie que la personne $i$ a besoin de $r$ équipements de type $k$.

Le problème à modéliser est le suivant : Est-il possible d’assigner à chaque personne une salle qui réponde à ses besoins, et si oui quelle salle peut être assignée à chaque personne ?

"Indice

Il ne faut surtout pas confondre les constantes $E_{\text{jk}}$ et $B_{\text{ik}}$ avec les variables du modèle à produire. Les assignations de variables doivent permettre de dire quelle personne doit aller dans quelle salle. Le plus simple pour pouvoir exprimer ensuite les contraintes est d’utiliser des variables $X_{\text{ij}}$ à domaine {0,1}, où $i \in 1..P$ désigne une personne et $j \in 1..N$ désigne une salle. $X_{\text{ij}} = 1$ signifie que la personne $i$ va dans la salle $j$.

A vous maintenant de spécifier les contraintes.

"Indice

Il faut exprimer qu’une personne doit aller dans une salle et une seule. Pour ce faire, on pose la contrainte suivante pour chaque personne $i$ :

$$\Sigma_{j \in 1..N}X_{\text{ij}} = 1$$

Ensuite, il faut ajouter les contraintes permettant d’exprimer que les ressources de chaque salle sont suffisantes pour satisfaire les besoins des personnes qui s’y trouvent. A vous de jouer.

"Indice

Pour chaque salle $j$, $j \in 1..N$ et chaque ressource $k \in 1..M$, Il faut ajouter une contrainte qui exprime que les ressources de type $k$ de la salle $j$ sont suffisantes pour tous les occupants de cette salle. Au total, il y aura donc $\text{NM}$ contraintes. Tentez d’exprimer ces contraintes.

"Solution"

On doit avoir les contraintes suivantes :

Pour tout $j \in 1..N$ et tout $k \in 1..M$, $\Sigma_{i \in 1..P}B_{\text{ik}}X_{\text{ij}} \leq E_{\text{jk}}$.

Le problème est complètement modélisé.

Programmation par contraintes en M2 informatique

Programmation par contraintes : partie A

Programmation par contraintes : partie B

Programmation par contraintes : partie C

Programmation par contraintes : partie I

Programmation par contraintes : partie A

Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Partie A : Satisfaction de contraintes

Objectif

Connaître et comprendre les notions de base de la programmation par contrainte avec variables à domaines finis.

Prérequis

Notions de mathématiques de niveau Lycée.

Introduction

La programmation par contraintes permet de résoudre de nombreux problèmes sans avoir à réaliser un programme spécifique pour chaque problème à résoudre. Le principe est de modéliser le problème à résoudre sous la forme d’un réseau de contraintes qui sera placé en entrée d’un solveur.

Dans ce cours, nous nous limiterons aux contraintes sur des variables à domaines finis, qui permettent de modéliser des problèmes combinatoires.

A1 : Notions de base

Présentation

Un réseau de contraintes est constitué de variables, de domaines associés à ces variables et de contraintes reliant certaines de ces variables. Les contraintes peuvent être décrites en compréhension, c’est à dire par des formules mathématiques, ou en extension, c’est à dire par énumération des valeurs conjointement admissibles des variables concernées.

Exemple

Énoncé en langage naturel

Peut-on colorier les sommets du graphe suivant avec trois couleurs en faisant en sorte que les sommets reliés par une arête aient toujours des couleurs différentes ? Et si oui donnez une solution.

Modélisation en compréhension

Variables : $A,B,C,D,E,F$ ayant toutes pour domaine ${1,2,3}$.

Contraintes :

$A\neq B,A\neq C,B\neq C,C\neq D,D\neq E,D\neq F,E\neq F$

Modélisation en extension

Variables : $A,B,C,D,E,F$ ayant toutes pour domaine ${1,2,3}$.

Contraintes :

$q_1$ sur $A,B$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_2$ sur $A,C$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_3$ sur $B,C$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_4$ sur $C,D$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_5$ sur $D,E$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_6$ sur $D,F$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$
$q_7$ sur $E,F$ : ${(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)}$

Une solution

Exercices de découverte

A-dec-10

Donnez une représentation en extension de la contrainte sur les variables $A,B,C$ ayant toutes pour domaine ${0,1,2}$ dont la représentation en compréhension est $A+B=C$.

"Solutions"

Sur $A,B$ : ${(0,0,0),(0,1,1),(1,0,1),(0,2,2),(2,0,2),(1,1,2)}$

A2 : Quelques définitions

Assignation :

Une assignation d’une variable $V$ consiste à lui attribuer une valeur x de son domaine. On peut la noter $V=x$ ou $(V, x)$.

Une assignation complète d’un ensemble de variables est un ensemble d’assignations attribuant une valeur à chaque variable de cet ensemble.

Une assignation partielle d’un ensemble de variable est un ensemble d’assignations attribuant une valeur à certaines variables de cet ensemble.

Étendre, compatibilité :

Soit $V$ un ensemble de variables, $J$ une assignation partielle de $V$ et $I$ une assignation complète de $V$. On dit que $I$ étend $J$, ou est compatible avec $J$ si et seulement si toutes les variables assignées par $J$ sont assignées avec la même valeur dans $I$.

Satisfaire, falsifier :

Soit $V$ l’ensemble des variables reliées par une contrainte $Q$. On dit d’une assignation complète $I$ de $V$ qu’elle satisfait $Q$ si et seulement si les valeurs attribuées aux variables sont autorisées par $Q$. Dans le cas contraire, on dit que $I$ falsifie $Q$.

On dit d’une assignation partielle $J$ de $V$ qu’elle satisfait $Q$ si et seulement si toute assignation complète compatible avec $J$ satisfait $Q$. On dit qu’elle falsifie $Q$ si et seulement si toute assignation complète compatible avec $J$ falsifie $Q$.

Exemple

La contrainte ALLDIFF, appliquée à un ensemble de variables, est satisfaite si et seulement si toutes les variables concernées sont assignées à des valeurs différentes. Dans la figure ci-dessous, les domaines des variables sont représentés par des rectangles.

Voici une assignation complète et une assignation partielle qui satisfont la contrainte.

Et voici une assignation complète et une assignation partielle qui falsifient la contrainte.

Réseau de contraintes cohérent :

Une solution d’un réseau de contraintes est une assignation complète de ses variables qui satisfait toutes ses contraintes.

Un réseau de contrainte est cohérent si et seulement s’il admet au moins une solution. Dans le cas contraire il est dit incohérent.

Exercices de découverte

A-dec-20

Soient les variables $A,B,C$ ayant toutes pour domaine ${0,1}$. Donnez une assignation complète qui étend l’assignation partielle ${A=1}$.

"Solution"

Par exemple ${A=1,B=0,C=0}$. Il y en a trois autres.

A-dec-21

Soient deux variables $A,B$ ayant le même domaine de $k$ éléments. Combien d’assignations complètes des variables satisfont la contrainte $A\neq B$ ?

"Solution"

$k^2 – k$

Récapitulatif

Vous venez de découvrir beaucoup de termes que vous n’avez pas encore complètement assimilé. Reprenez-les sur la figure suivante et tentez de retrouver le sens de chacun d’eux. Si vous n’y arrivez pas, revenez en arrière dans ce document pour relire les parties concernées.

Exercices d’assimilation

A-ass-00

Voici un réseau de contraintes. Variables : $A,B,C$ de domaine ${1,2,3,4}$. Contraintes :

$q_1$ : $A+B\leq C$
$q_2$ : $A\neq B$

Ce réseau est-il cohérent ? Si oui, donnez ses solutions. Donnez une assignation partielle de ${A,B,C}$ attribuant une valeur uniquement à la variable $A$ qui falsifie $q_1$.

"Indice

${A=1,B=2,C=3}$ est une solution. Trouvez les autres.

"Indice

Voici les solutions avec $A=1$ : ${A=1,B=2,C=3}, {A=1,B=2,C=4}, {A=1,B=3,C=4}$ Il vous reste à trouver celles avec $A=2$, celles avec $A=3$ (il n’y en a pas avec $A=$4).

"Indice

Voici toutes les solutions. ${A=1,B=2,C=3}, {A=1,B=2,C=4}, {A=1,B=3,C=4}$ ${A=2,B=1,C=3}, {A=2,B=1,C=4}, {A=2,B=3,C=4}$ ${A=3,B=1,C=4}$ Il vous reste à trouver une valeur de $A$ qui ne permet pas de satisfaire $q_1$, quelles que soient les valeurs de $B$ et $C$.

"Solution"

${A=4}$ falsifie $q_1$.

A-ass-01

Voici un réseau de contraintes. variables : $A,B,C\in {1,2,3}$. contraintes :

$q_1$ sur $A,B$ : ${(1,1),(1,2),(2,3),(3,3)}$
$q_2$ sur $A,C$ : ${(2,2),(3,1)}$
$q_3$ sur $B,C$ : ${(2,1),(3,3)}$

Ce réseau est-il cohérent ? Si oui, donnez ses solutions.

"Indice

La représentation graphique ci-dessous, dans laquelle les couples de valeurs autorisés par les contraintes sont matérialisés par des lignes reliant les valeurs concernées, doit vous permettre de trouver plus rapidement les solutions, si applicable.

"Indice

Dans la figure ci-dessus, toute solution (s’il y en a) apparait sous la forme d’un triangle dont les sommets sont les valeurs assignées aux variables.

"Solution"

Le réseau est incohérent.

A-ass-02

Voici un réseau de contraintes. Variables : $A,B,C,D,E\in {0,1}$. Contraintes :

$A\vee \neg B$
$B\vee \neg C$
$C\vee \neg D$
$D\vee \neg E$
$\neg A\vee B$
$\neg B\vee C$
$\neg C\vee D$
$\neg D\vee E$

Où le symbole $\vee$ est le connecteur logique « ou ». Ce réseau est-il cohérent ? Si oui, donnez ses solutions.

"Indice

Trouvez d’abord la solution pour laquelle la variable A vaut 0 en faisant des déductions basées sur les 4 premières contraintes. Puis ensuite trouvez la solution pour laquelle A vaut 1 en exploitant les 4 dernières contraintes.

"Indice

Pour $A=0$, la première contrainte ne peut être satisfaite qu’avec $B=0$. Donc pour satisfaire la deuxième contrainte, il faut $C=0$, pour la troisième, $D=0$, pour la quatrième $E=$0. Avec ces valeurs, les 4 dernières contraintes sont satisfaites. Tenter de trouver l’autre solution.

"Solution"

Les deux solutions sont ${A=0,B=0,C=0,D=0}$ et ${A=1,B=1,C=1,D=1}$.

CC2 des M2 BDIA avec corrigé

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

Variables : $A, C$ de domaine $\{1,2,3\}$, $B,D$ de domaine $\{4,5,6\}$.

Contraintes :

Sur $A,B$ : $\{(1,5),(2,6),(3,4)\}$.
Sur $B,C$ : $\{(4,2),(5,3),(6,1)\}$.
Sur $C,D$ : $\{(1,5),(2,6),(3,4),(3,6)\}$.
Sur $A,D$ : $\{(1,6),(2,4),(3,5)\}$.

"Solution"

Une solution : $A=1, B=5, C=3, D=6$.

A2 (1 point)

Donnez la spécification en extension de la contrainte logique $A\vee \neg B \vee C$.

"Solution"

Sur $A,B,C$ : $\{(0,0,0),(0,0,1),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}$.

Partie B

Soit $V$ un ensemble de variables, $q$ une contrainte reliant les variables de $V$ et un ensemble $Q$ de contraintes tel que les variables reliées par chaque contrainte de $Q$ appartiennent à $V$.

On dit que $Q$ est équivalent à $q$ si et seulement si toute assignation complète des variables de $V$ satisfait toutes les contraintes de $Q$ si et seulement si elle satisfait $q$.

Par exemple, l’ensemble de contraintes $Q = \{A\neq B, A\neq C, B\neq C\}$ est équivalent à la contrainte $q = \text{allDiff}(A,B,C)$.

On appelle contrainte logique toute contrainte spécifiée en compréhension uniquement à l’aide des opérateurs $\vee, \wedge, \neg$.

Dans les questions suivantes, il sera uniquement question de variables Booléennes, donc à domaine $\{0,1\}$.

B1 (1 point)

Donnez un ensemble de contraintes logiques équivalent à la contrainte $X_1+…+X_N \neq 0$. Cet ensemble peut ne contenir qu’une seule contrainte.

"Solution"

$X_1\vee…\vee X_N$

B2 (1 point)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $A+B+C+D \leq 2$.

"Solution"

$(\neg A \vee \neg B \vee \neg C)$, $(\neg A \vee \neg B \vee \neg D)$, $(\neg A \vee \neg C \vee \neg D)$, $(\neg B \vee \neg C \vee \neg D)$

B3 (2 points)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $X_1+…+X_N \leq 1$, pour tout entier $N$ supérieur à 1.

"Solution"

$\forall i \in 1..N, \forall j \in i+1..N, (\neg X_i \vee \neg X_j)$

Partie C

Pour chacune des questions, vous devez répondre en donnant, dans un ordre plausible, les valeurs retirées lors de la restauration de la cohérence de domaines du réseau de contraintes ou de la contrainte donnée dans l’énoncé. Aucune justification n’est demandée. Vous devez juste donner, à raison d’une ligne par visite d’une contrainte, la liste des valeurs retirées en utilisant la notation $V\neq x$ pour dire que la valeur $x$ est retirée du domaine de $V$.

Par exemple pour décrire le filtrage du réseau $q_1 : A<B$, $q_2 : B<C$ où $A, B, C$ ont pour domaine $\{1,2,3\}$, vous devez adopter la présentation suivante :

$q_1$ : $A\neq 3, B\neq 1$
$q_2$ : $B\neq 3, C\neq 1, C\neq 2$
$q_1$ : $A\neq 2$

C1 (2points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A$ de domaine $\{1,2,3\}$, $B$ de domaine $\{4,5,6\}$, $C$ de domaine $\{7,8,9\}$.

Contraintes :

$q_1$ sur $A,B$ : $\{(1,5),(2,4),(3,6)\}$
$q_2$ sur $B,C$ : $\{(4,8),(5,7),(6,8)\}$
$q_3$ sur $A,C$ : $\{(1,7),(2,8),(3,9)\}$

"Solution"

$q_2 : C\neq 9$
$q_3 : A\neq 3$
$q_1 : B \neq 6$

C2 (2 points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A,B,C$ de domaine $\{1,2,3\}$.

Contraintes :

$q_1$ : $A+B+C=6$
$q_2$ : $A+2B+C=9$
$q_3$ : $2A+B+3C=10$

"Solution"

$q_2 : B\neq 1$
$q_3 : A\neq 3, C\neq 3$
$q_1 : A\neq 1$
$q_2 : B\neq 2, C \neq 2$

Partie D

D1 (2 points)

Soit le réseau de contraintes suivant :

Variables : $A,B,C,D$ ayant toutes pour domaine $\{3,7,11\}$.

Contraintes :

$A+B+C+D \leq 17$
$A+B+C+D \geq 17$

Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.

"Solution"

CC2 des M2 BDIA

Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

Variables : $A, C$ de domaine $\{1,2,3\}$, $B,D$ de domaine $\{4,5,6\}$.

Contraintes :

Sur $A,B$ : $\{(1,5),(2,6),(3,4)\}$.
Sur $B,C$ : $\{(4,2),(5,3),(6,1)\}$.
Sur $C,D$ : $\{(1,5),(2,6),(3,4),(3,6)\}$.
Sur $A,D$ : $\{(1,6),(2,4),(3,5)\}$.

"Solution"

Une solution : $A=1, B=5, C=3, D=6$.

A2 (1 point)

Donnez la spécification en extension de la contrainte logique $A\vee \neg B \vee C$.

"Solution"

Sur $A,B,C$ : $\{(0,0,0),(0,0,1),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)\}$.

Partie B

On dit que $Q$ est équivalent à $q$ si et seulement si toute assignation complète des variables de $V$ satisfait toutes les contraintes de $Q$ si et seulement si elle satisfait $q$.

Par exemple, l’ensemble de contraintes $Q = \{A\neq B, A\neq C, B\neq C\}$ est équivalent à la contrainte $q = \text{allDiff}(A,B,C)$.

On appelle contrainte logique toute contrainte spécifiée en compréhension uniquement à l’aide des opérateurs $\vee, \wedge, \neg$.

Dans les questions suivantes, il sera uniquement question de variables Booléennes, donc à domaine $\{0,1\}$.

B1 (1 point)

Donnez un ensemble de contraintes logiques équivalent à la contrainte $X_1+…+X_N \neq 0$. Cet ensemble peut ne contenir qu’une seule contrainte.

"Solution"

$X_1\vee…\vee X_N$

B2 (1 point)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $A+B+C+D \leq 2$.

"Solution"

$(\neg A \vee \neg B \vee \neg C)$, $(\neg A \vee \neg B \vee \neg D)$, $(\neg A \vee \neg C \vee \neg D)$, $(\neg B \vee \neg C \vee \neg D)$

B3 (2 points)

Donnez un ensemble de contraintes logiques aussi petit que possible équivalent à la contrainte $X_1+…+X_N \leq 1$, pour tout entier $N$ supérieur à 1.

"Solution"

$\forall i \in 1..N, \forall j \in i+1..N, (\neg X_i \vee \neg X_j)$

Partie C

Par exemple pour décrire le filtrage du réseau $q_1 : A<B$, $q_2 : B<C$ où $A, B, C$ ont pour domaine $\{1,2,3\}$, vous devez adopter la présentation suivante :

$q_1$ : $A\neq 3, B\neq 1$
$q_2$ : $B\neq 3, C\neq 1, C\neq 2$
$q_1$ : $A\neq 2$

C1 (2points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A$ de domaine $\{1,2,3\}$, $B$ de domaine $\{4,5,6\}$, $C$ de domaine $\{7,8,9\}$.

Contraintes :

$q_1$ sur $A,B$ : $\{(1,5),(2,4),(3,6)\}$
$q_2$ sur $B,C$ : $\{(4,8),(5,7),(6,8)\}$
$q_3$ sur $A,C$ : $\{(1,7),(2,8),(3,9)\}$

"Solution"

$q_2 : C\neq 9$
$q_3 : A\neq 3$
$q_1 : B \neq 6$

C2 (2 points)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

Variables : $A,B,C$ de domaine $\{1,2,3\}$.

Contraintes :

$q_1$ : $A+B+C=6$
$q_2$ : $A+2B+C=9$
$q_3$ : $2A+B+3C=10$

"Solution"

$q_2 : B\neq 1$
$q_3 : A\neq 3, C\neq 3$
$q_1 : A\neq 1$
$q_2 : B\neq 2, C \neq 2$

Partie D

D1 (2 points)

Soit le réseau de contraintes suivant :

Variables : $A,B,C,D$ ayant toutes pour domaine $\{3,7,11\}$.

Contraintes :

$A+B+C+D \leq 17$
$A+B+C+D \geq 17$

"Solution"