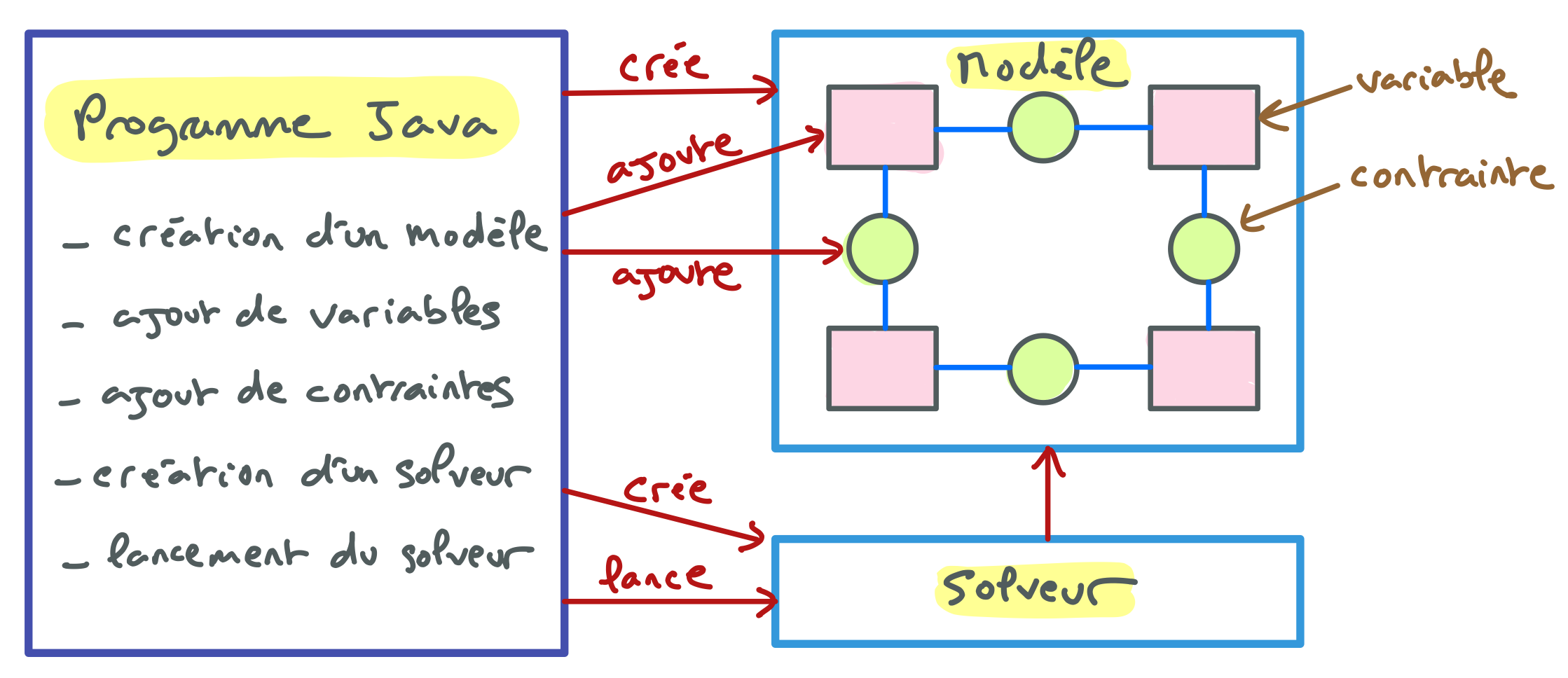
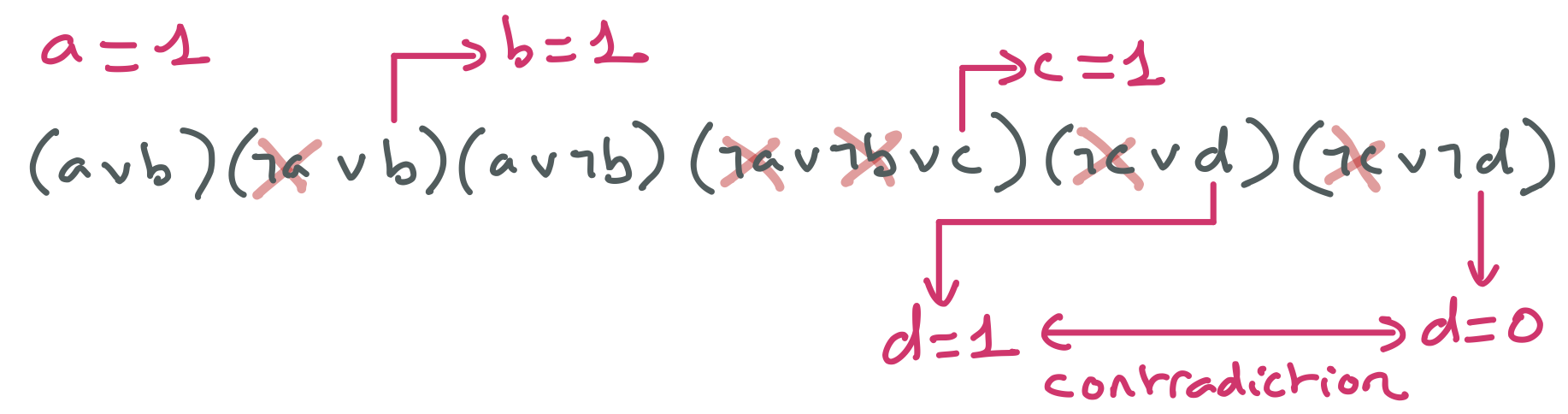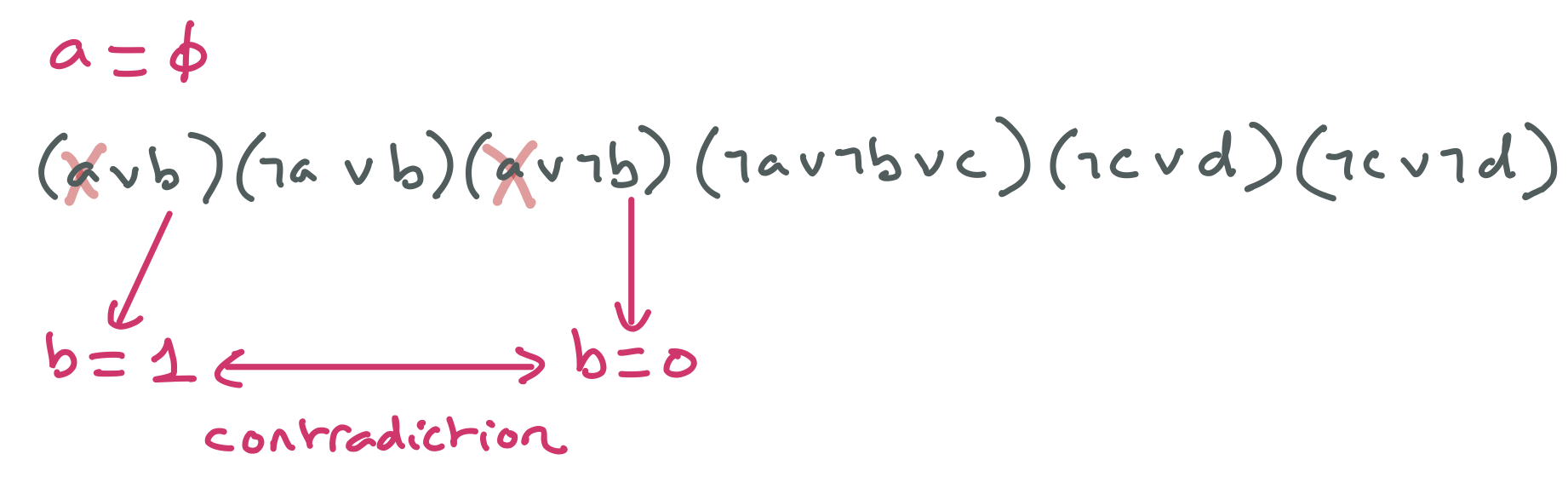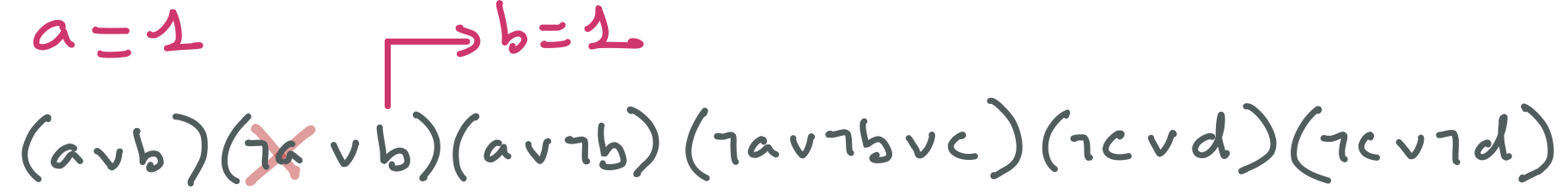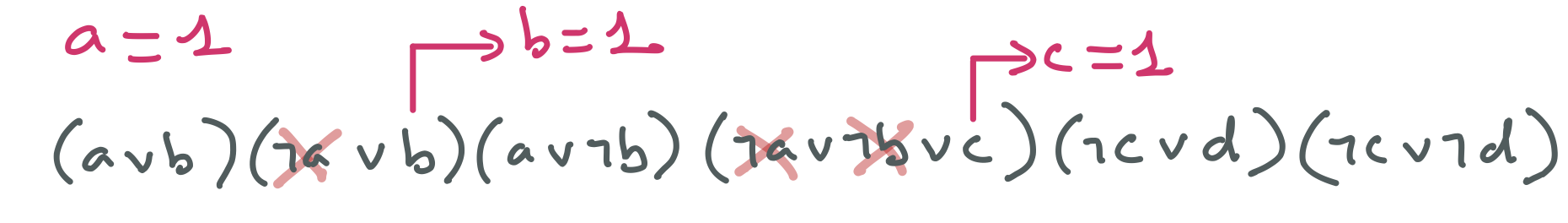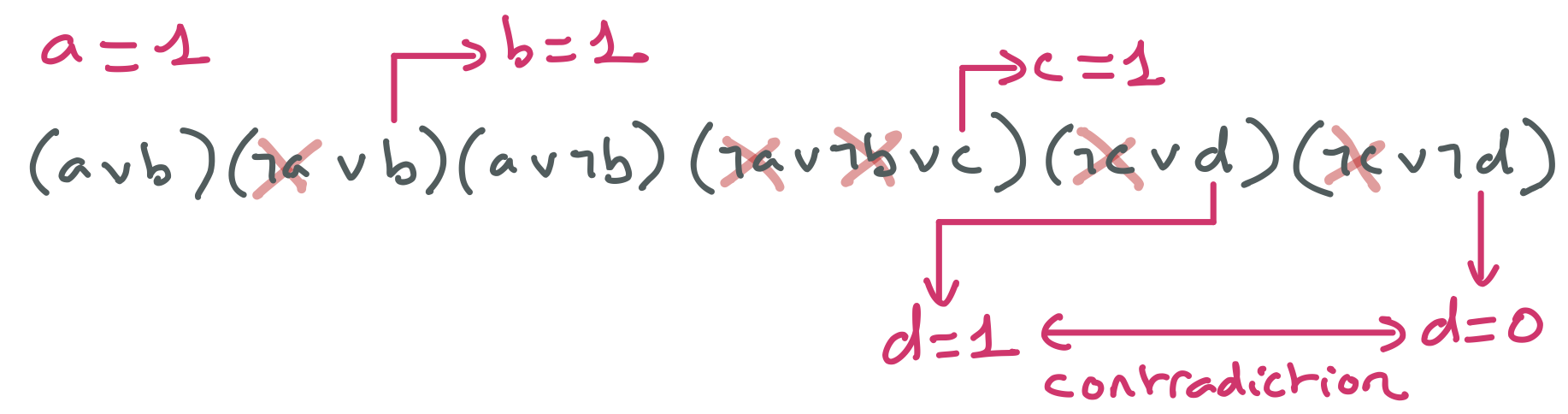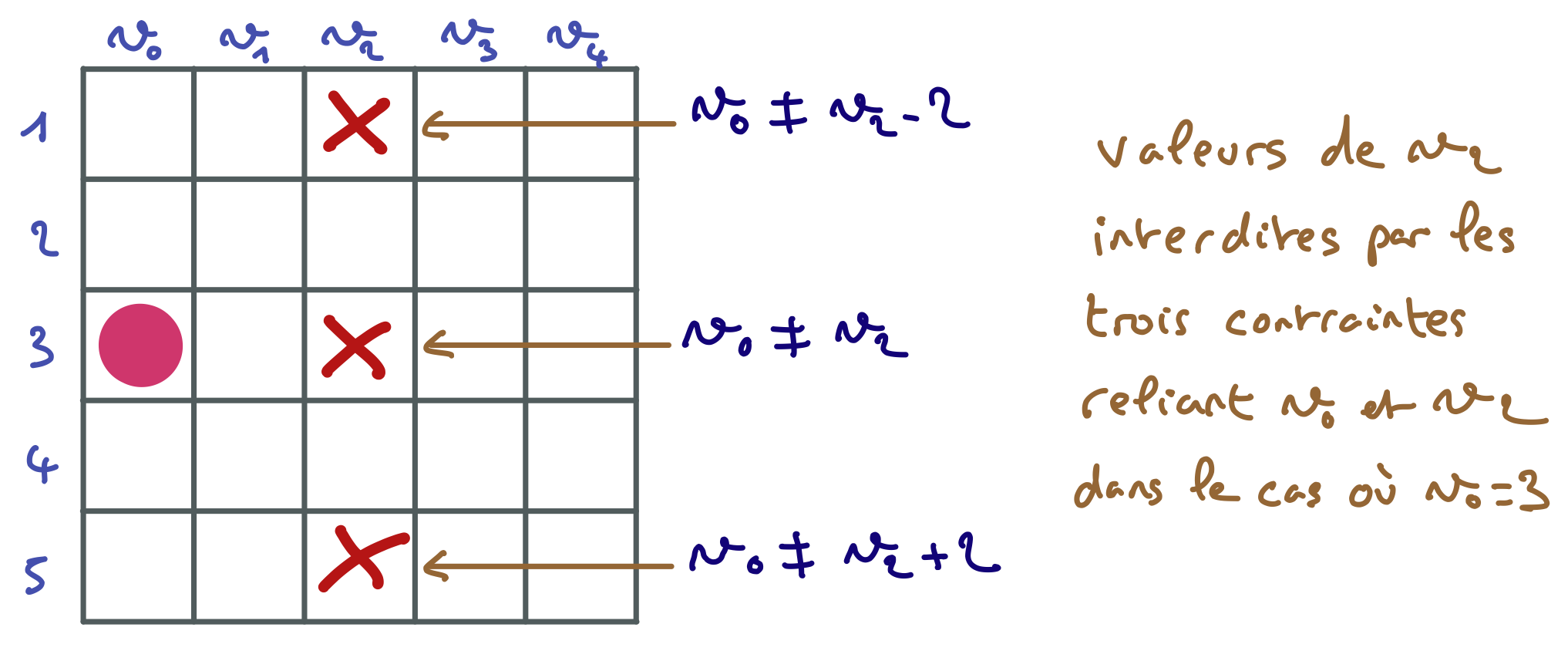Programmation par contraintes
En M2 Bases de données et IA et M2 Image et IA
Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne
Partie D : résolution énumérative
Objectif
Comprendre le principe de fonctionnement d’un solveur de type MAC (Maintaining Arc Consistency) et être capable de simuler le déroulement de l’exécution d’un tel solveur sur une instance de problème dont l’arbre de recherche peut être dessiné sur une feuille A4, et d’énumérer ou comptabiliser les solutions (si applicable) de cette instance.
Prérequis
Parties A et C
Introduction
Résoudre un réseau de contraintes, c’est déterminer s’il existe au moins une assignation des variables qui satisfait toutes les contraintes. Le nombre de ces assignations étant proprement astronomique – il croît exponentiellement en fonction du nombre de variables – il n’est pas possible en pratique d’énumérer et de tester une par une toutes les assignations possibles.
La résolution dite « énumérative » ne l’est donc pas totalement mais fait aussi appel à des déductions pour accélérer la recherche d’éventuelle solutions. Dans le cas du solveur MAC que nous allons étudier, ces déductions sont des restaurations de cohérence de domaines.
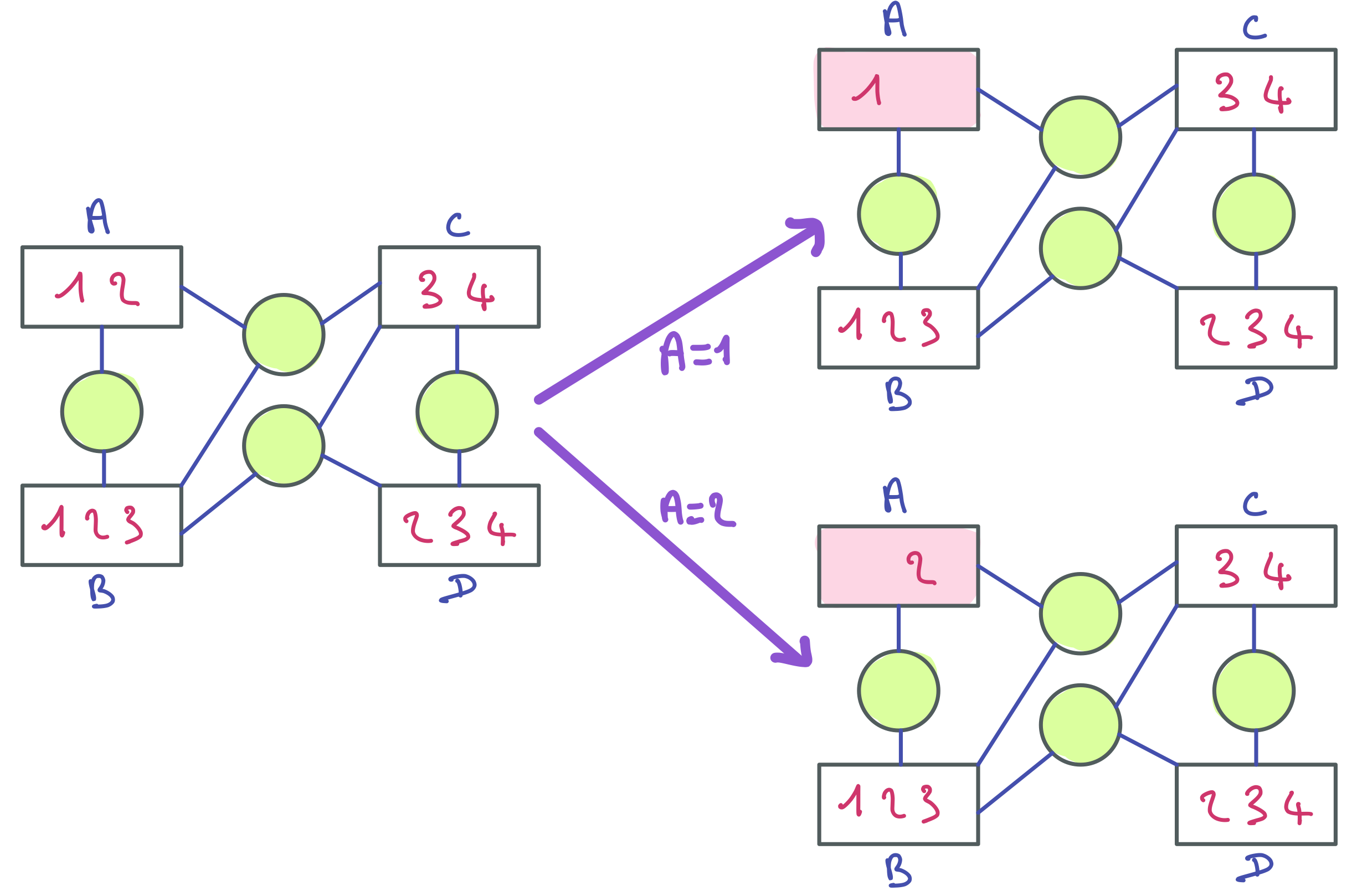
L’idée de l’algorithme MAC est de décomposer le réseau de contraintes à résoudre, après restauration de la cohérence de domaines, en plusieurs réseaux plus simples dans lesquels une des variables du réseau initial a été assignée avec une des valeurs de son domaine. Par exemple, un réseau ayant une variable A de domaine {1, 2} sera décomposé en deux réseaux : un dans lequel la variable A vaut 1 et un dans lequel elle vaut 2. Chacun de ses réseaux sera filtré et si nécessaire, à nouveau décomposé sur la base d’une autre variable. La variable A est appelée variable de branchement.
D-dec-10
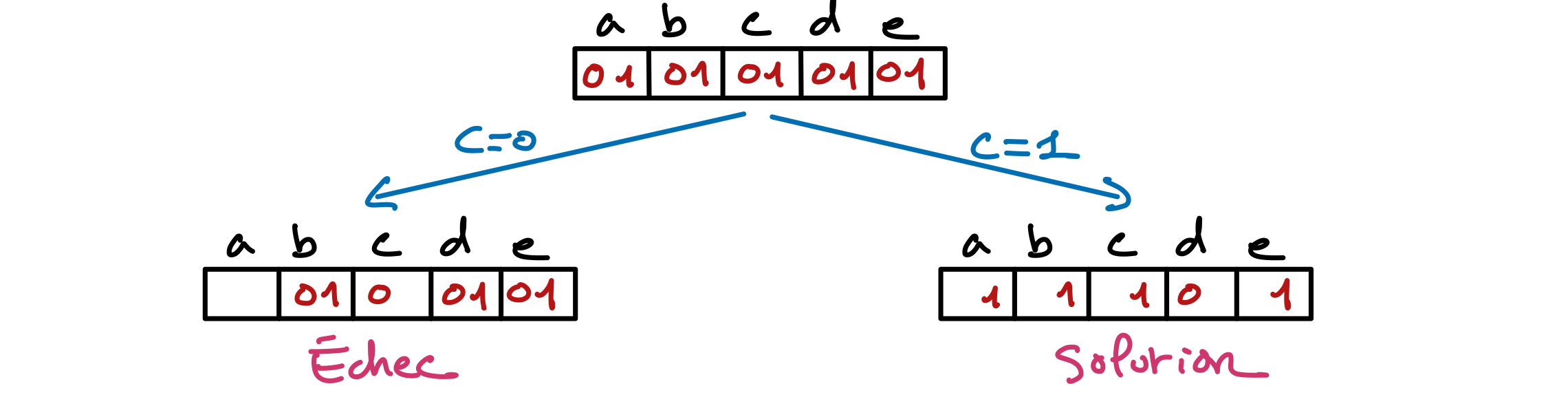
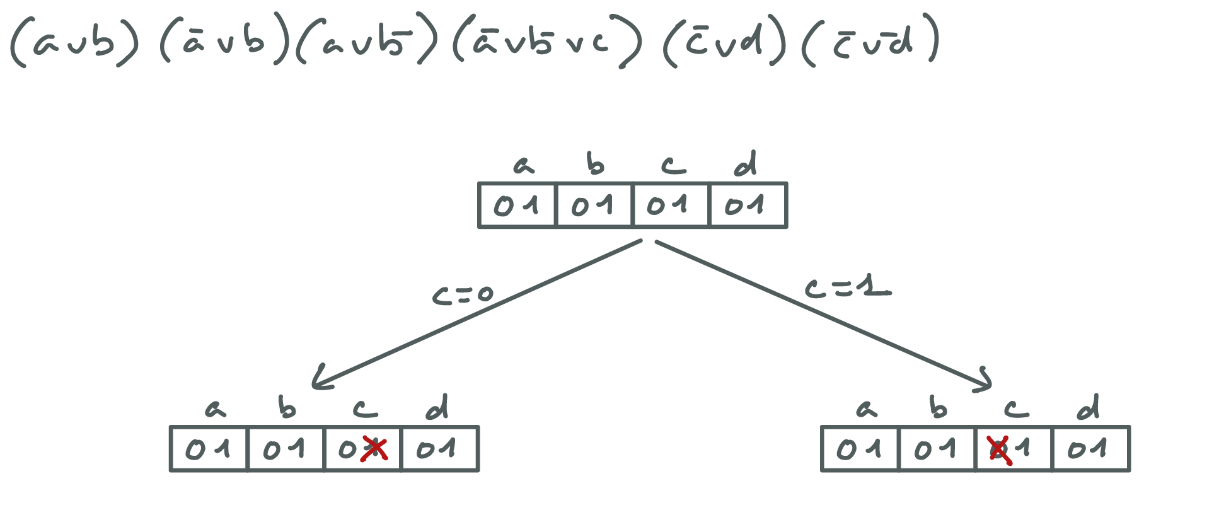
Soit le réseau de contraintes $(a\vee b \vee c), (\neg a \vee \neg c), (\neg b \vee c)$, où les variables $a,b,c$ ont toutes pour domaine ${0,1}$. Donnez les réseaux obtenus pour $a=0$ et $a=1$.
"Solution"
- $a=0$ : $(b \vee c), (\neg b \vee c)$
- $a=1$ : $(\neg c), (\neg b \vee c)$
En effet, pour $a=0$, la contrainte $(\neg a\vee \neg c)$ est satisfaite, on peut donc la retirer du réseau. D’autre part, la contrainte $(a\vee b \vee c)$ peut se simplifier en $(b \vee c)$.
Pour $a=1$, je vous laisse vérifier par vous-même les simplifications.
D2 : Algorithme MAC
Cette version de l’algorithme produit toutes les solutions. On peut la modifier pour qu’elle s’arrête dès qu’une solution est trouvée.

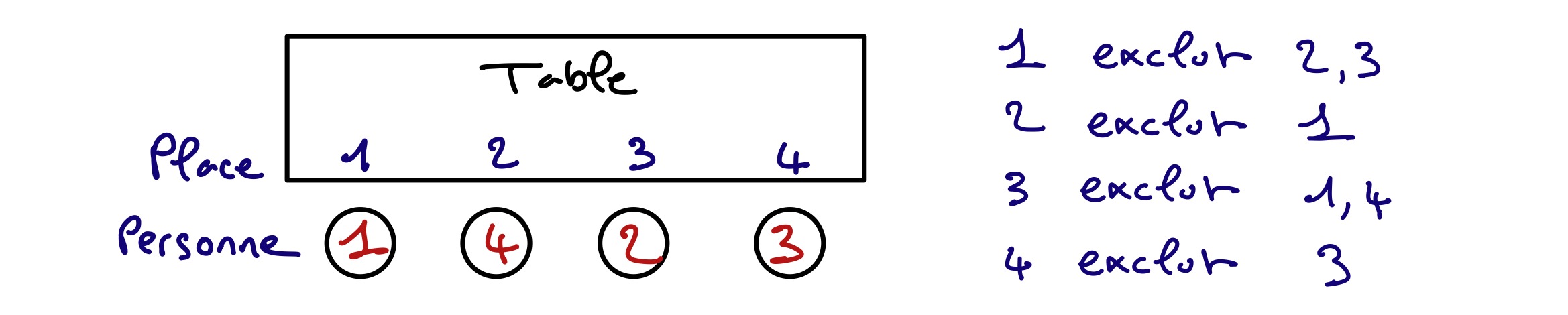
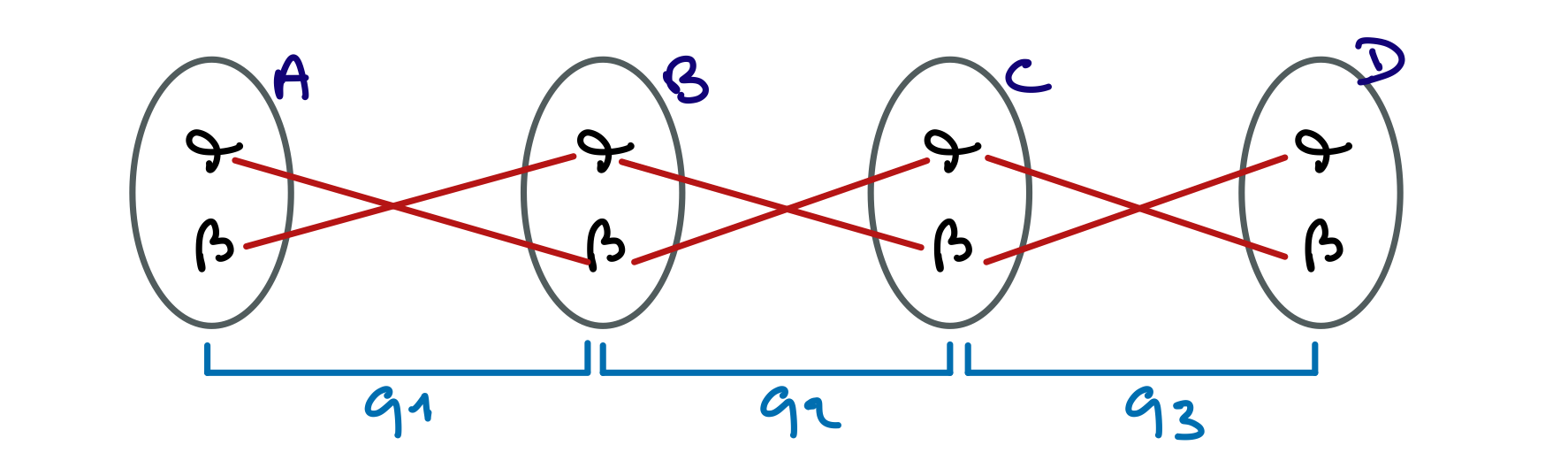
Simulons l’exécution de cet algorithme sur le réseau suivant :
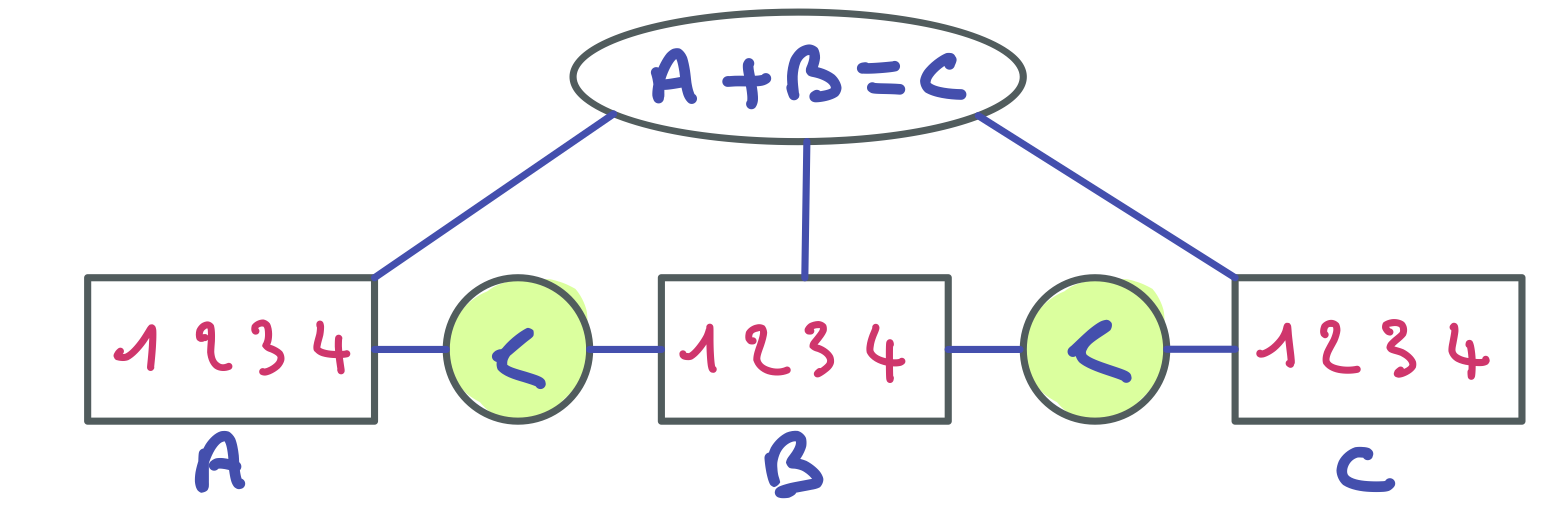
La première chose à faire est de restaurer la cohérence de domaines. Cela peut permettre de simplifier le problème avant de faire le premier branchement. Voici le résultat du filtrage.
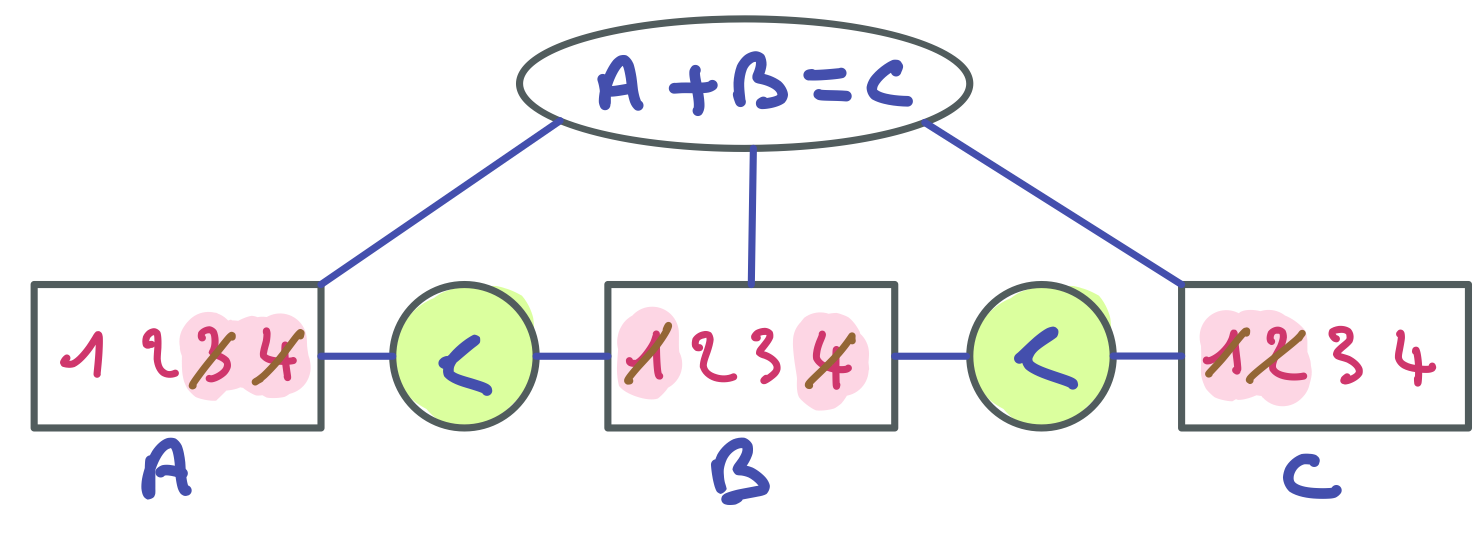
Si ce résultat vous paraît étonnant, c’est que vous ne maîtrisez pas le badge C, qui est un prérequis (où que le rédacteur du présent document s’est trompé).
Le filtrage simplifie le réseau (ce n’est pas toujours le cas), mais ne produit pas immédiatement de solution et ne fait pas apparaître d’incohérence (domaine vide).
Il nous faut donc choisir une variable de branchement. Nous allons utiliser la variable A. Nous obtenons l’arbre de recherche suivant, qui permet d’énumérer les deux solutions du réseau. Selon les besoins, on peut arrêter la recherche à la première solution ou n’énumérer qu’une partie des solutions. Si toute les branches de l’arbre de recherche aboutissent à une incohérence (domaine vide après filtrage), on conclut à l’incohérence du réseau.
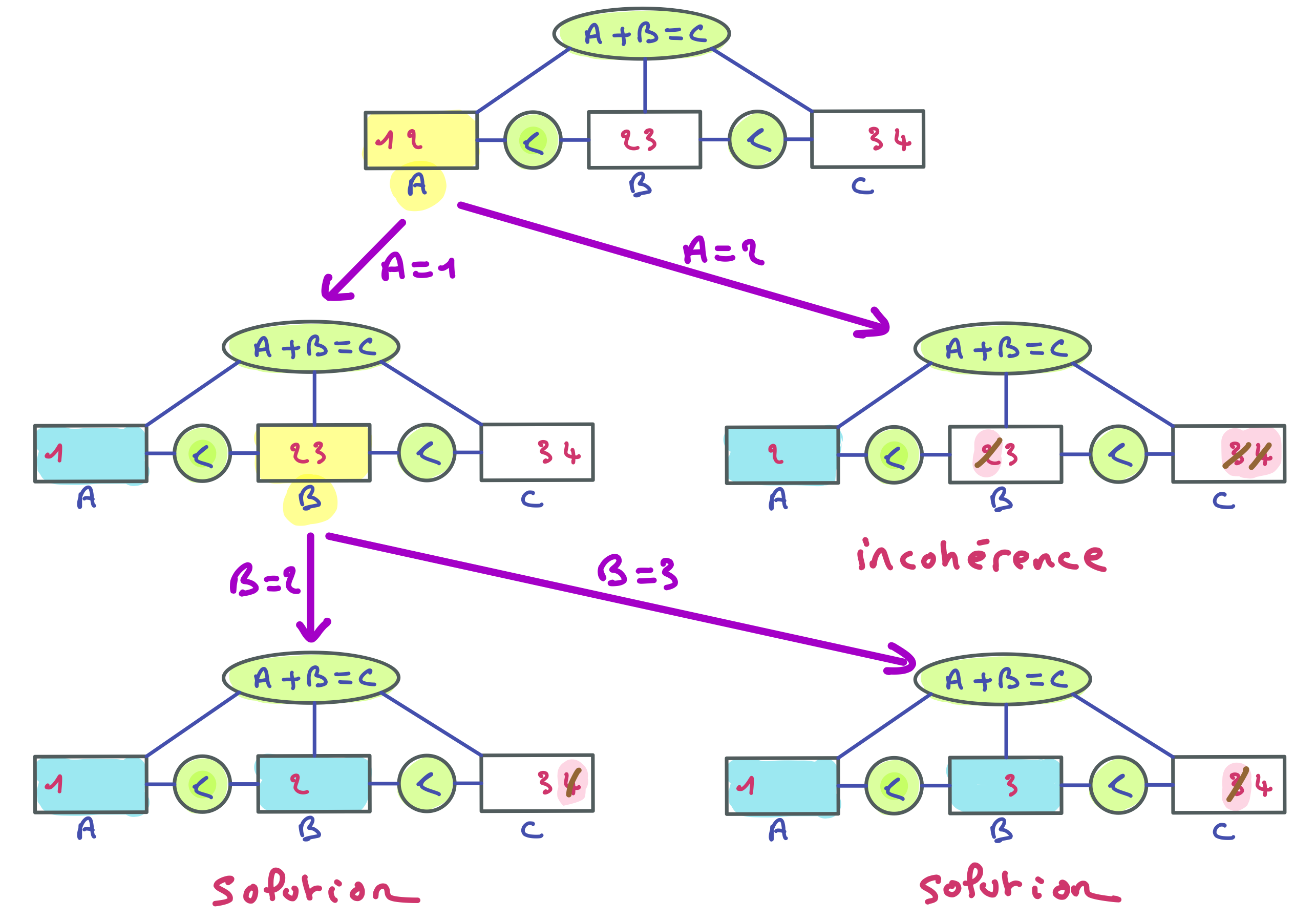
En pratique, pour présenter une simulation de résolution, on ne redessinera pas tout le réseau de contraintes à chaque nœud, mais seulement les domaines et les variables de branchement.
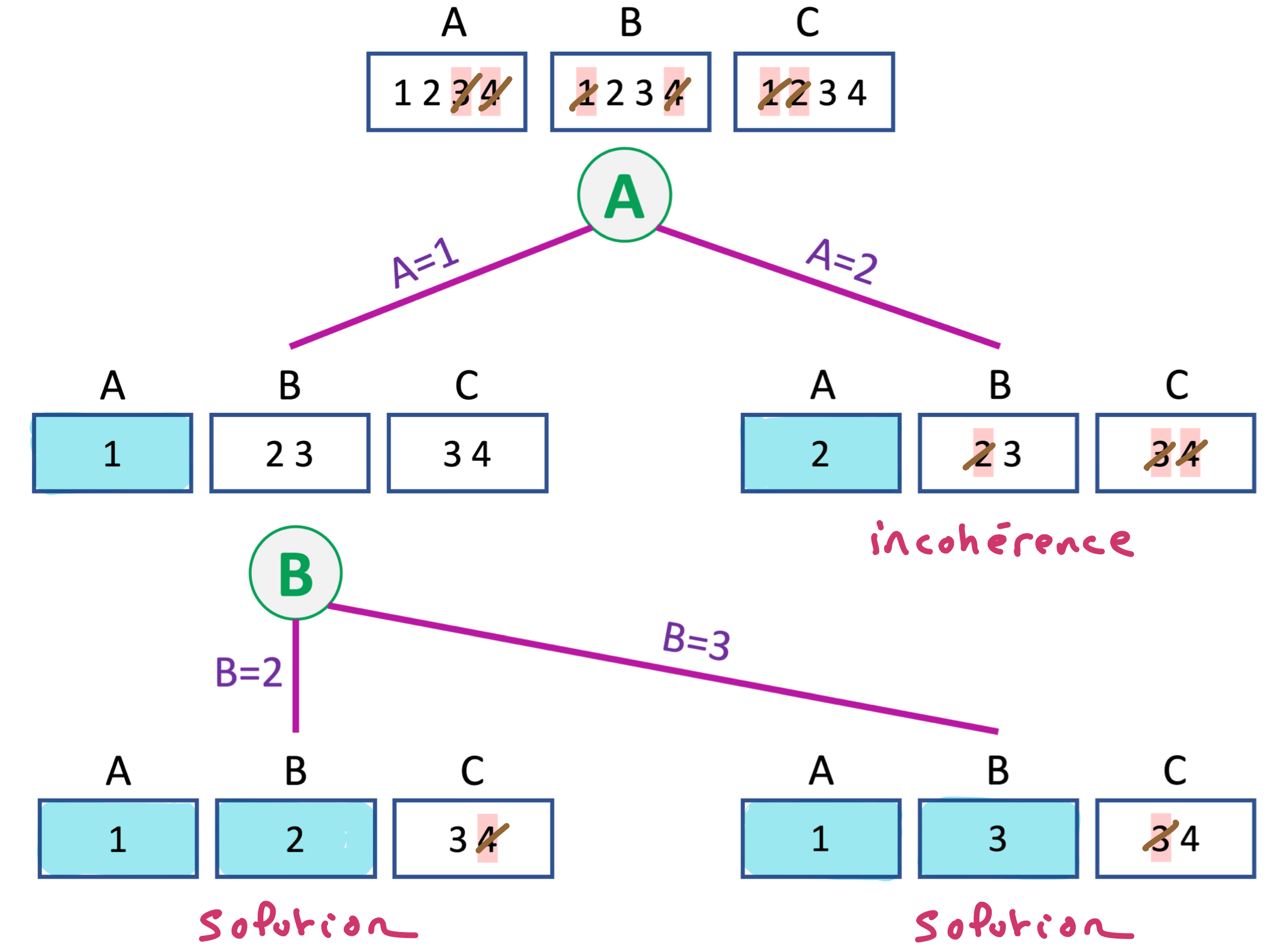
D-dec-20
Est-il plus avantageux, moins avantageux ou aussi avantageux d’utiliser la variable $B$ comme variable de branchement à la racine de l’arbre de recherche ?
"Solution"
C’est plus avantageux car pour $B=2$, on déduit $A\neq 2$ puis $C\neq 4$ par filtrage et on obtient une solution. Pour $B=3$, on déduit $C \neq 3$ puis $A \neq 2$ par filtrage et on obtient la deuxième solution. On a donc un seul branchement au lieu de deux.
D3 : variantes
Filtrage affaibli
Dans l’algorithme MAC, un filtrage complet par restauration de cohérence de domaine est réalisé à chaque nœud (y compris racine) de l’arbre de recherche. Ce filtrage est généralement rentable dans la mesure où le temps qu’il consomme est largement compensé par la réduction du nombre de branchements, donc de la taille de l’arbre de recherche. Mais il peut y avoir des exceptions pour certaines contraintes dont la restauration de cohérence de domaines est couteuse, pour lesquelles on peut utiliser un filtrage plus « faible ».
Par exemple, restaurer la cohérence de domaine sur une contrainte de type $a_{1} x_{1} + \ldots + a_{n} x_{n} = b$, où $a_{1}, \ldots, a_{n}$ et $b$ sont des entiers relatifs, est très couteux. On ne connait aucun algorithme capable de le faire en temps polynomial. (Ce qui est contre-intuitif !)
On peut utiliser à la place un filtrage très rapide bien que moins puissant, qui consiste à restaurer la cohérence de domaine sur les deux contraintes $a_{1} x_{1} + \ldots + a_{n} x_{n} \leq b$ et $a_{1}\ x_{1} + \ldots + a_{n} x_{n} \geq b$. Même si cela vous paraît très étrange en première lecture, restaurer la cohérence de domaine sur les deux inégalités ne permet pas de la restaurer sur l’égalité.
Pas convaincu ?
D-dec-30
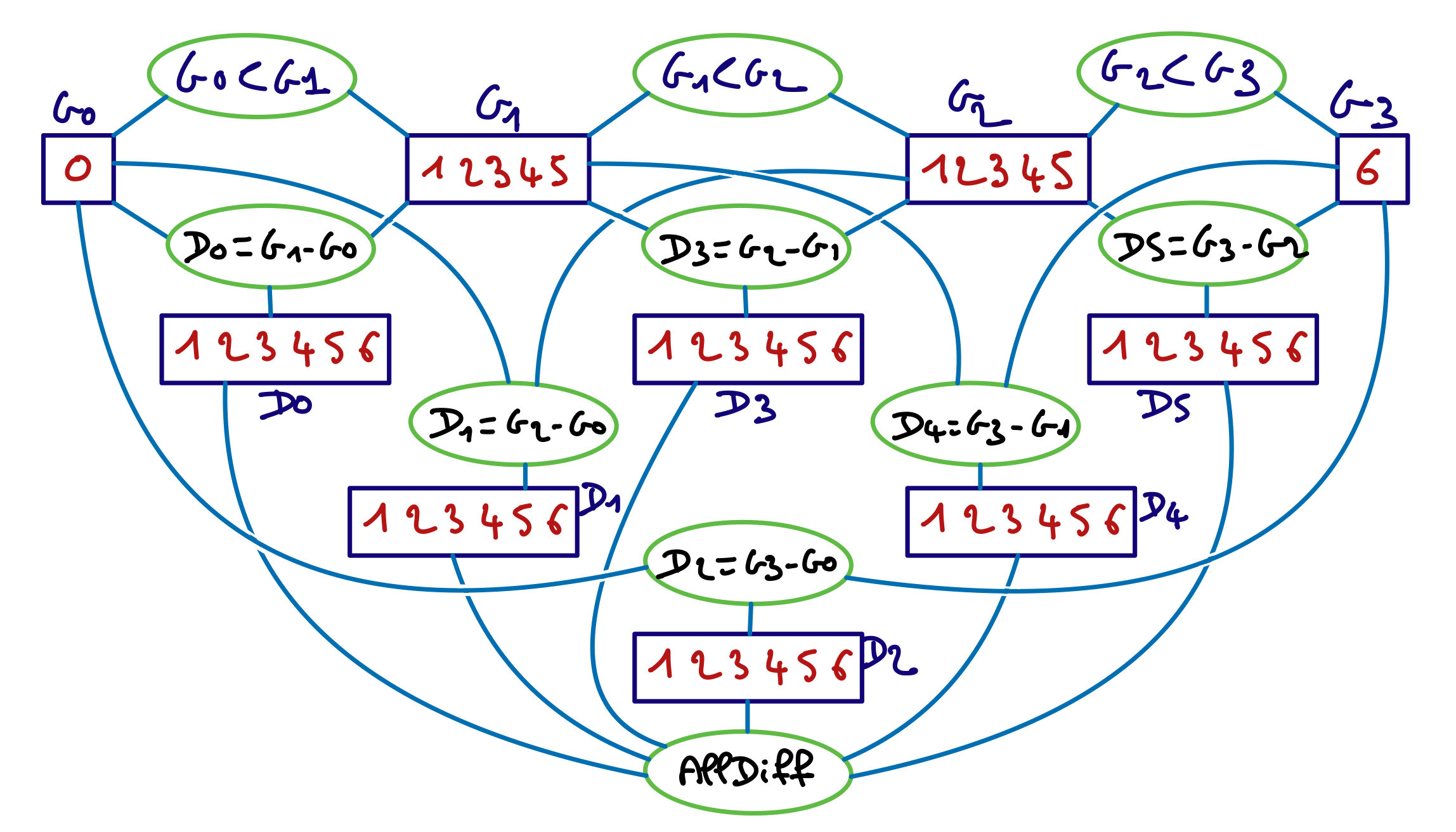
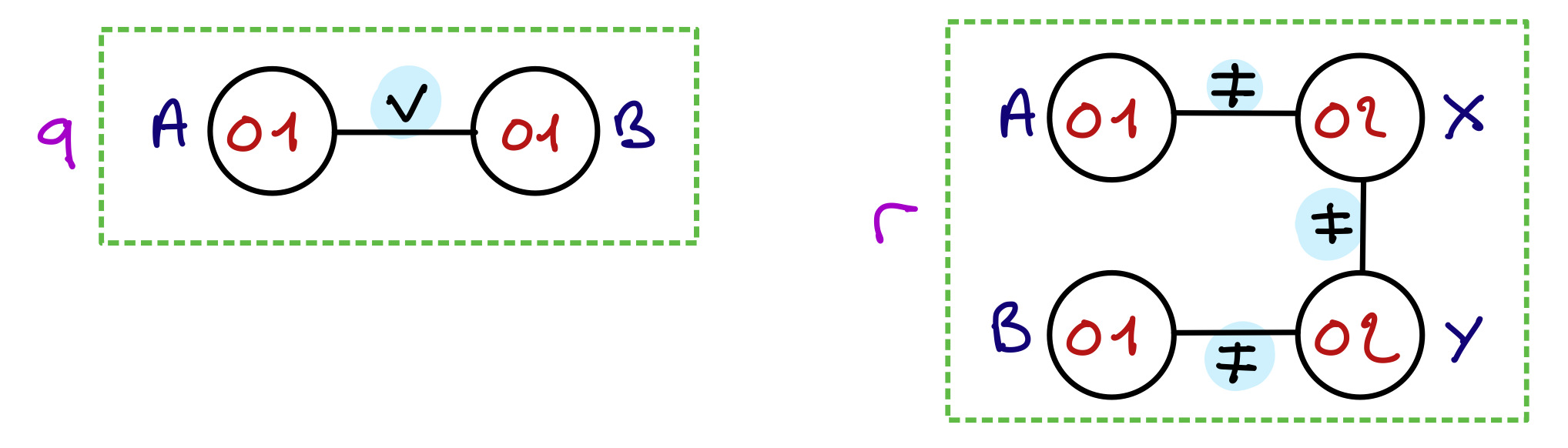
Restaurez la cohérence de domaine sur le réseau de contraintes suivant, avec domaine {0,1} pour toutes les variables :
"Solution"
On ne peut retirer aucune valeur des domaines en considérant les deux contraintes séparément. Si vous ne voyez pas pourquoi, c’est que le badge C n’est pas complètement acquis. Vous avez peut-être été en excès de confiance si vous pensiez le maîtriser.
En effet, en mettant n’importe laquelle des variables à 0, on peut toujours trouver une manière d’assigner les autres variables pour obtenir une somme au moins égale à 6 et une manière de les assigner pour obtenir une somme au plus égale à 6. Il en va de même en assignant n’importe quelle variable à 1.
D-dec-31
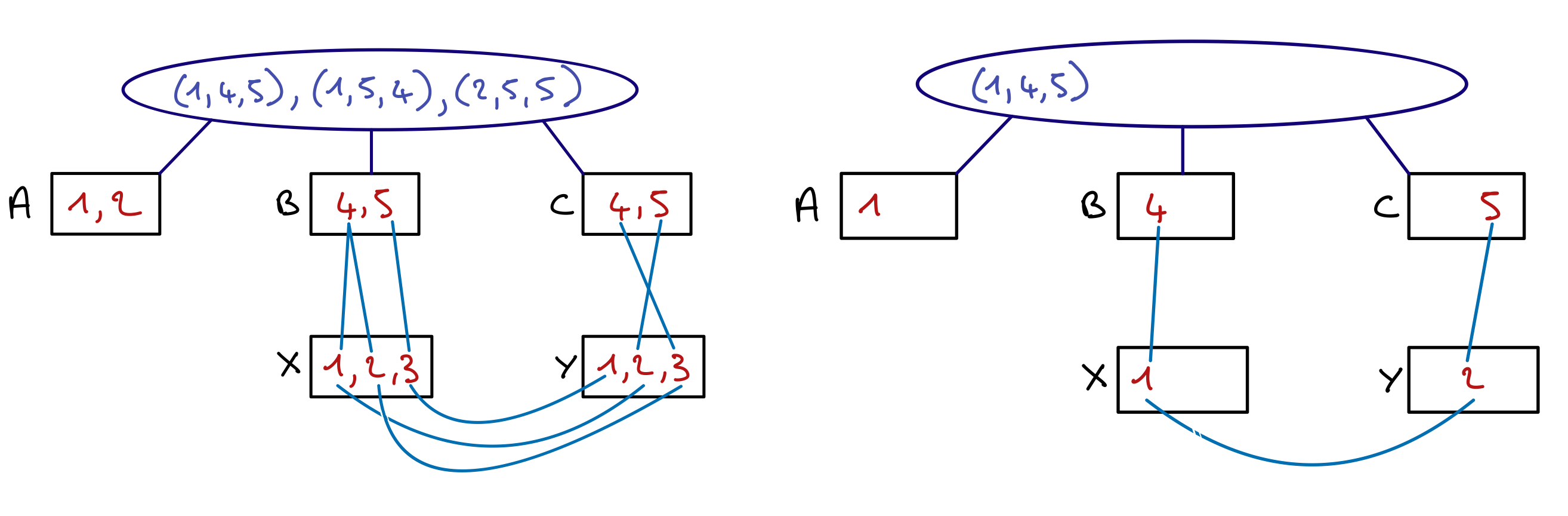
A présent, toujours avec les mêmes domaines initiaux {0,1}, restaurez la cohérence de domaine sur la contrainte suivante :
- $q : x_{1} + 2x_{2} + 3x_{3} + 4x_{4} = 6$
Ce n’est pas immédiat à réaliser. Il faut se poser des questions du genre « est-il possible d’obtenir une somme égale à 6 si $x_{1}$ vaut 1 ? »
"Solution"
La réponse est oui. Il suffit d’assigner $x_{2} = 1, x_{3} = 1,x_{4} = 0$. Donc $x_{1} = 1$ a un support, et donc on ne retire pas 1 du domaine de $x_{1}$. En faisant un raisonnement similaire pour les autres valeurs, on obtient les domaines respectifs suivants pour les variables $x_{1}$ à $x_{4}$ : {0,1}, {1}, {0,1}, {0,1}.
La restauration de la cohérence de domaines sur $q$ a permis de faire un filtrage qui n’a pas été réalisé par la restauration de la cohérence de domaines sur $q_{1}$ et $q_{2}$. Mais faute de disposer d’un algorithme efficace pour les contraintes telles que $q$, c’est-à-dire les égalités pseudo-Booléennes, on peut appliquer à ces contraintes des filtrages moins puissants qui restaurent la cohérence de domaines sur leur décomposition en deux inégalités pseudo-Booléennes.
Dans certains cas, contrairement à ce qui s’est produit dans notre exemple, ce filtrage affaibli réduit certains domaines et c’est mieux que rien.
Filtrage partiel
La restauration de cohérence de domaines s’applique itérativement à toutes les contraintes d’un réseau jusqu’à ce que toutes les valeurs de chaque domaine aient au moins un support pour toutes les contraintes. On peut réduire le coût du filtrage – et son efficacité – en ne filtrant que les contraintes directement reliées à la variable de branchement. L’algorithme obtenu est appelé forward checking (FC).
MAC est en général plus rapide que FC, mais on ne peut en faire un dogme. Dans certains cas particuliers où le filtrage complet serait couteux et peu rentable, on peut envisager d’utiliser FC, en prolongeant toutefois le filtrage lorsque certains domaines deviennent des singletons.
Dans le cadre de cet enseignement, on travaillera uniquement avec MAC.
Au delà de la cohérence de domaines
La restauration de la cohérence de domaines déduit tout ce qu’il est possible de déduire à partir d’une seule contrainte et lorsque la conclusion de la déduction est une restriction des domaines. Mais on peut imaginer d’autres formes de déductions faisant intervenir plusieurs contraintes. Lorsque le résultat d’une telle déduction est une nouvelle contrainte, on parlera d’apprentissage, mais si le résultat est une restriction de domaines on peut encore parler de filtrage.
L’exemple typique est la notion de k-cohérence, souvent appelée k-consistance dans la littérature par francisation du terme anglais consistency qui se dit en français cohérence. Un réseau de contraintes et k-cohérent si toute assignation partielle de k-1 variables peut être étendue à une assignation partielle de k variables sans falsifier de contrainte.
Cette notion ne sera pas développée ici, mais rien n’empêche de remplacer dans un solveur de type MAC la restauration de la cohérence de domaines par la restauration de la k-cohérence. Le risque est que le coût d’un tel filtrage soit plus élevé que son bénéfice, mais rien ne permet d’affirmer qu’il ne soit pas rentable pour certains types de contraintes ou de réseaux.
Branchements binaires
Dans l’algorithme MAC décrit au début de ce document, chaque nœud de l’arbre de recherche est associé à une certaine variable de branchement, appelons-là $V$, et chaque branche partant de ce nœud correspond à une valeur du domaine de $V$. On peut donc avoir des nœuds à deux, trois, quatre branches et plus. On peut interpréter ces branchements comme des hypothèses. En branchant sur $V = x$, où $x$ est dans le domaine de $V$, on fait l’hypothèse qu’il existe au moins une solution pour laquelle $V = x$. Si cette hypothèse est vraie, on trouvera de telles solutions dans le sous-arbre induit par le branchement. Si elle est fausse, on aura acquis une connaissance, à savoir qu’avec les domaines considérés avant le branchement, il n’existe aucun moyen de satisfaire le réseau si $V = x$. Cette connaissance est enregistrée implicitement par le solveur grâce au mécanisme qu’il utilise pour éviter de faire à nouveau le branchement $V = x$ à partir du même nœud de son arbre de recherche. On parle parfois de phase de la variable de branchement.
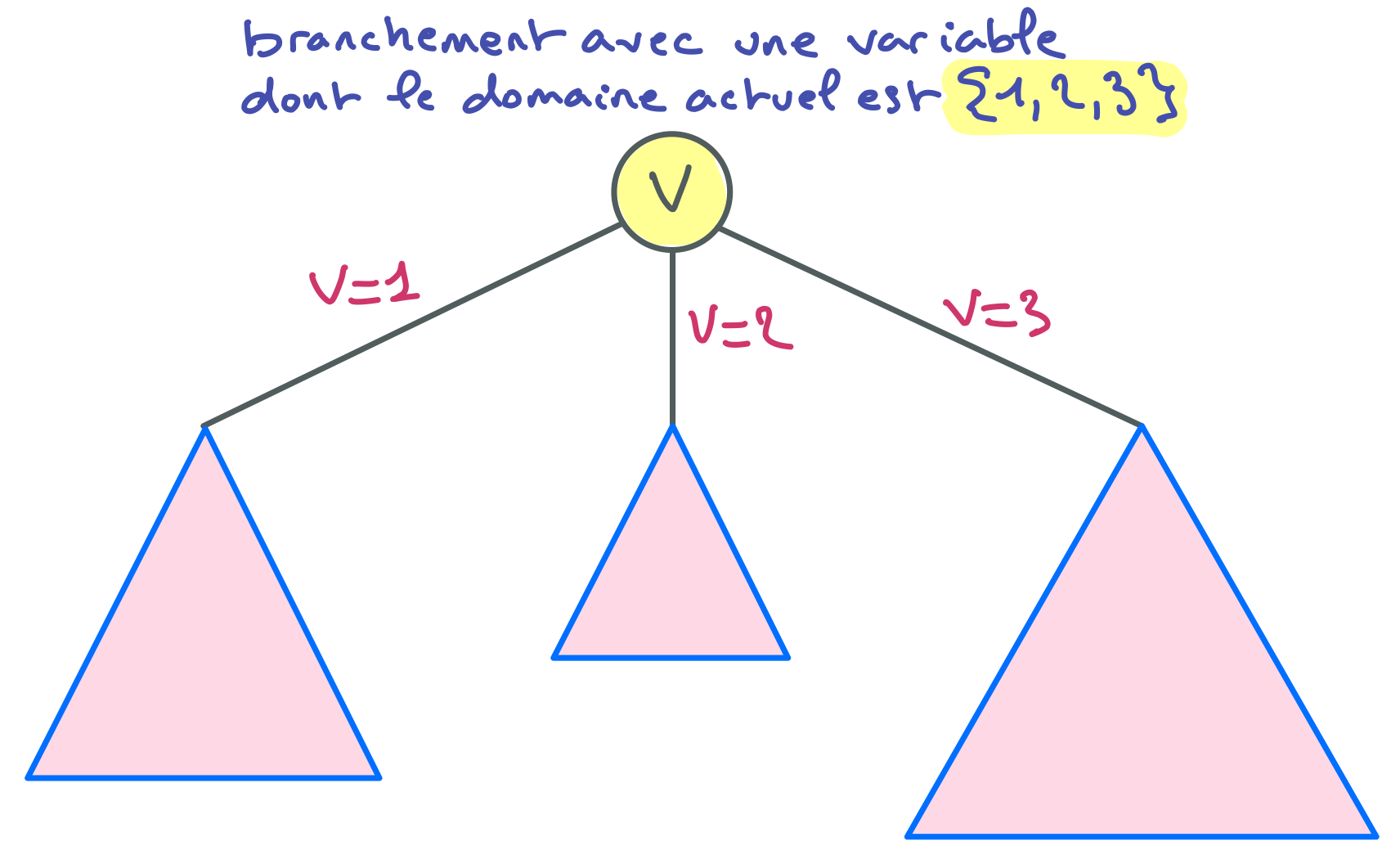
Il existe une variante de MAC dans laquelle on réalise exactement deux branchements à chaque nœud. Dans cette variante, pour une variable de branchement $V$, on va avoir un branchement correspondant à l’hypothèse $V = x$ et un autre correspondant à l’hypothèse $V \neq x$.
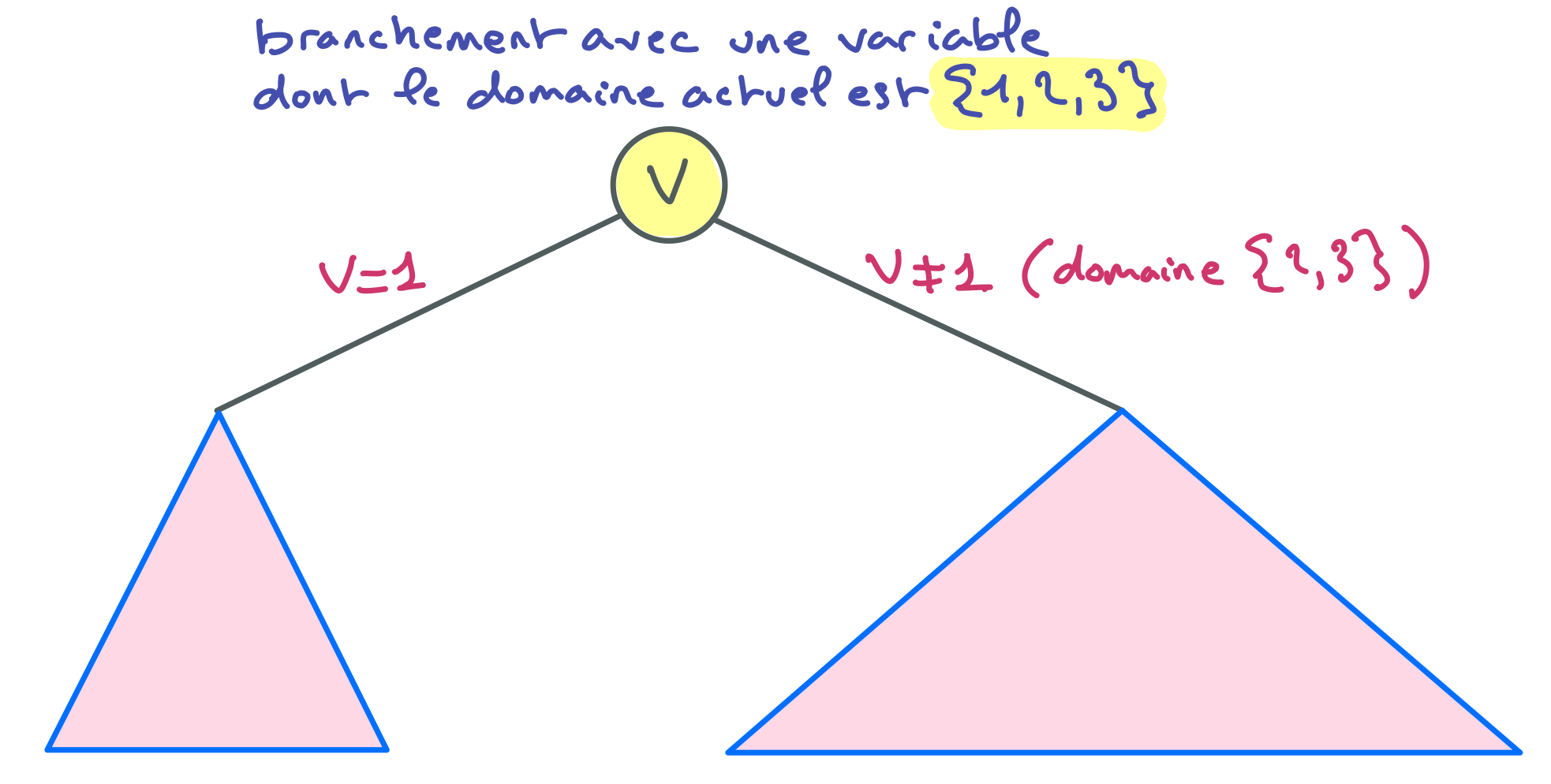
Tout arbre de MAC classique peut être aisément simulé par un MAC à branchements binaires. Par exemple dans le cas d’une variable de branchement $V$ de domaine ${ 1,2,3}$, le deuxième branchement correspondant à $V \neq 1$ pourra être prolongé par un branchement basé sur la même variable $V$ avec les hypothèses $V = 2$ et $V \neq 2$, mais comme à ce stade il n’y aura plus que 2 et 3 dans le domaine de $V$, cela reviendra au même que brancher sur $V = 2$ et $V = 3$.
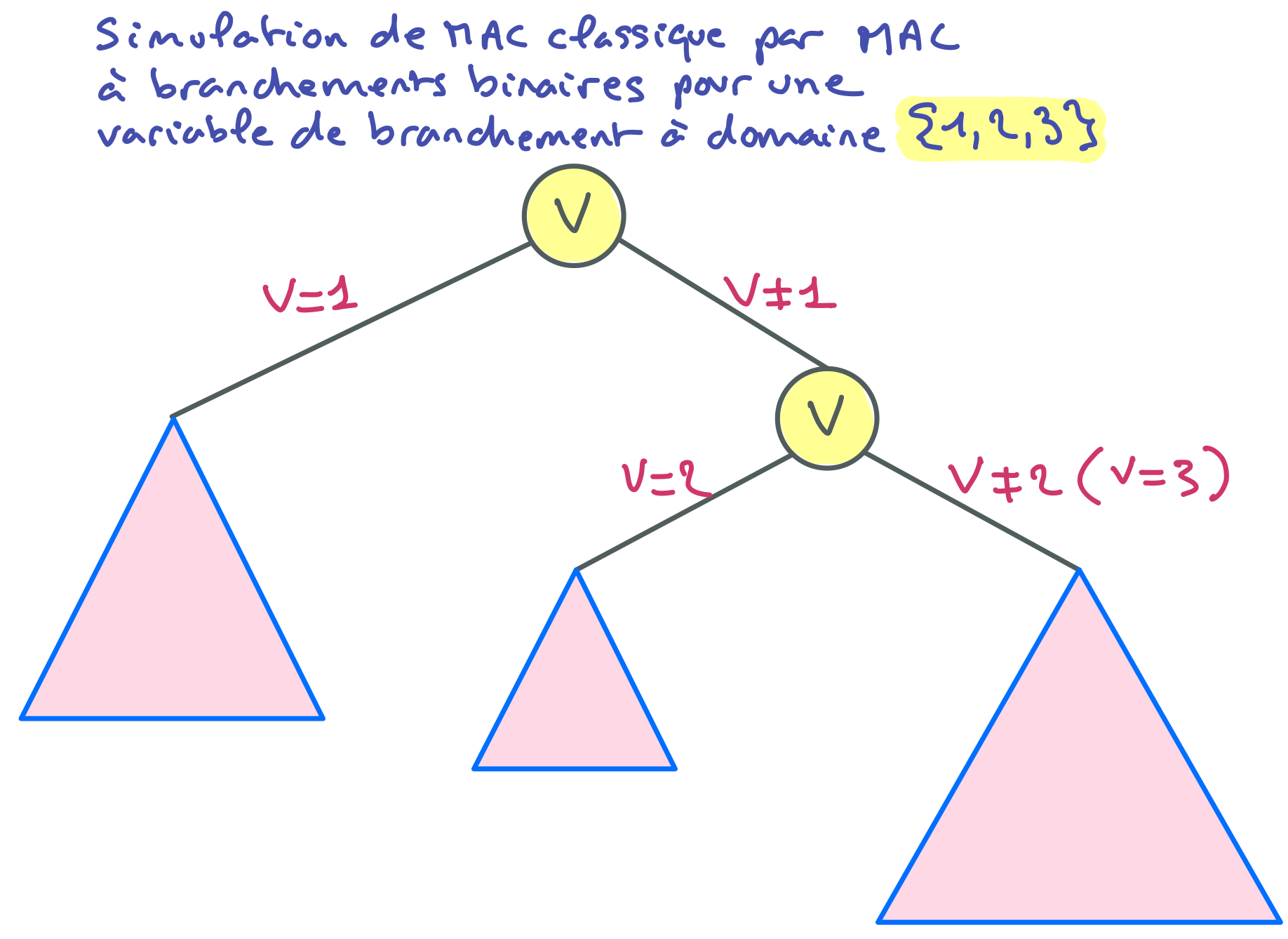
La réciproque n’est pas vraie. MAC à branchements binaires peut produire des arbres de recherche impossibles à obtenir avec MAC classique.
MAC à branchements binaires peut être plus efficace que MAC classique sur certains problèmes, à condition de bien choisir les variables et valeurs de branchements. Or ce choix est loin d’être évident, comme nous le verrons plus loin.
D-dec-32
Soit le réseau de contraintes suivant :
-
Variables : $A, B, C$ ayant toutes pour domaine ${1,2,3}$.
-
Contraintes : $\text{allDiff}(A,B,C)$, $A+B=4$.
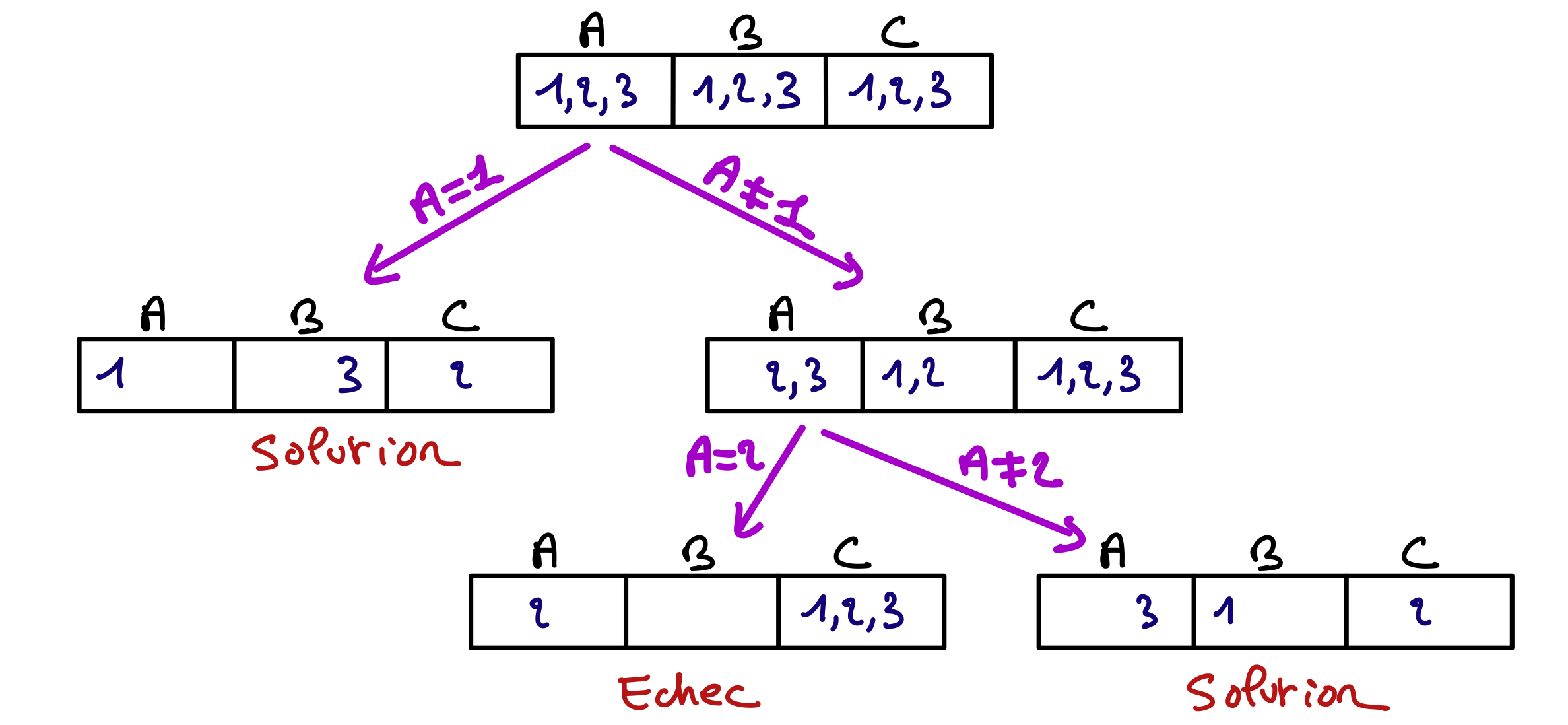
Donnez l’arbre de recherche MAC à branchement binaire en utilisant $A$ comme première variable de branchement.
Apprentissage (approfondissement hors programme)
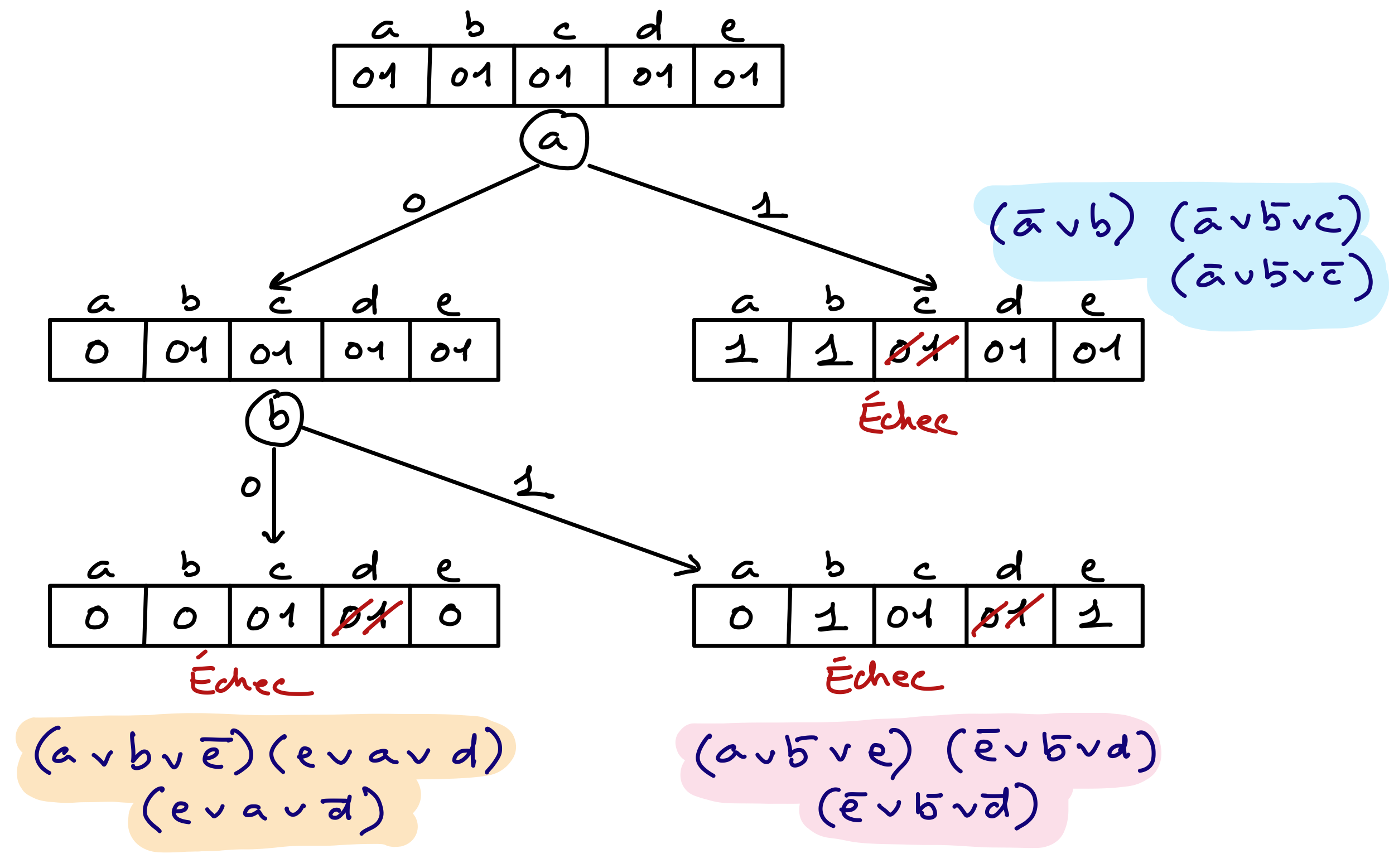
Dans MAC classique et MAC à branchements binaires, il y a une forme d’apprentissage dans le sens où le solveur accumule des connaissances sur des assignations partielles qui ne peuvent être étendues à des solutions. Prenons comme exemple l’arbre de recherche suivant (peu importe les contraintes).
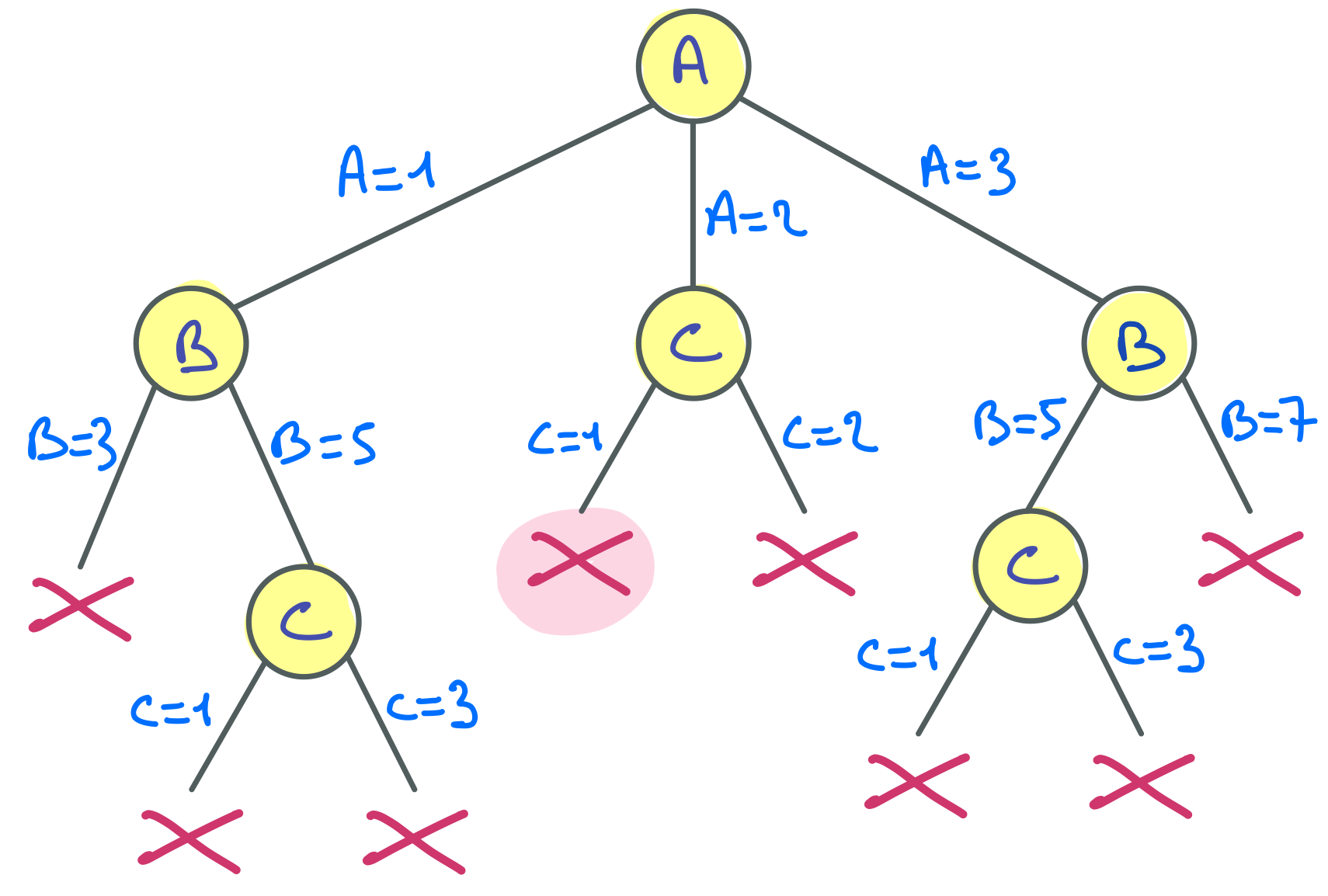
Cet arbre est parfaitement plausible. Rien n’oblige à choisir les variables de branchement dans le même ordre sur chaque branche. D’autre part, en raison des filtrages réalisés à chaque nœud, une même variable de branchement peut avoir un domaine différent selon le nœud où elle est utilisée. Les croix représentent des échecs, ou incohérences, c’est-à-dire des situations où après branchement et filtrage, un domaine devient vide.
Intéressons-nous au moment où la recherche vient de produire le quatrième échec. A ce moment précis, le solveur à accumulé les connaissances suivantes :
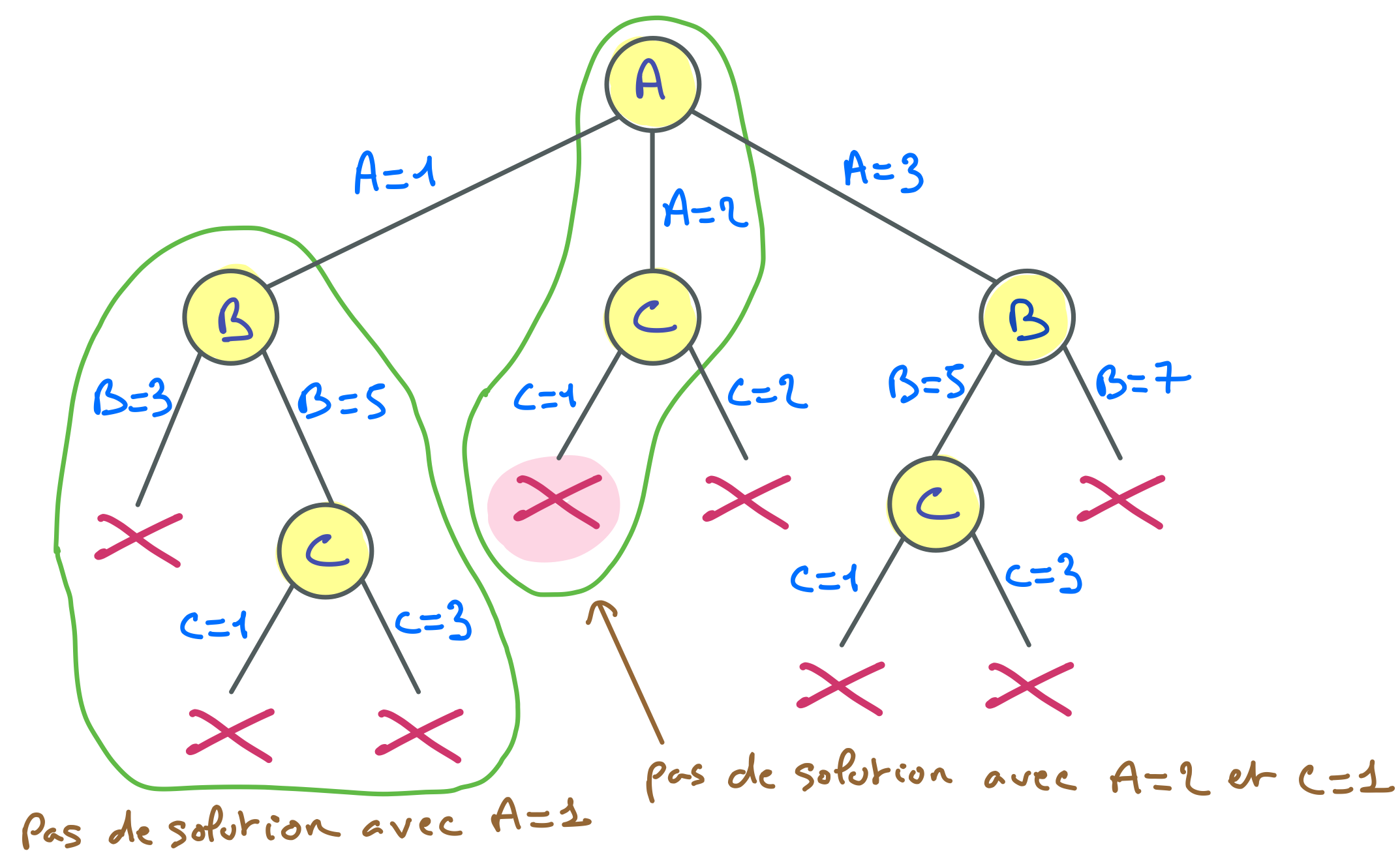
C’est ce que l’auteur de ce cours appelle de l’apprentissage implicite. C’est le mécanisme de retour arrière qui permet au solveur de conserver ces connaissances. Par exemple, après le stade matérialisé sur la figure ci-dessus, le solveur n’essaiera plus de trouver des solutions avec $A = 1$, ni avec $A = 2$ et $C = 1$.
Mais certains mécanismes d’apprentissage explicite peuvent être ajouté au solveur. Il peut s’agir de systèmes déductifs activés au moment des échecs. Par exemple, imaginons que le deuxième échec ne dépende pas de la valeur de la variable $A$. On dira que ${B = 5,\ C = 1}$ est un nogood. Trouver ce genre de nogood requiert des algorithmes spécifiques qui sortent du périmètre de ce cours.
Si notre algorithme MAC était équipé d’un mécanisme permettant de détecter le nogood ${B = 5,\ C = 1}$, alors on pourrait ajouter cette information dans une base de connaissances ou l’ajouter au réseau comme une nouvelle contrainte. Ainsi, si par exemple l’assignation $B = 5$ se reproduit plus tard, la valeur $1$ sera retirée du domaine de $C$, ce qui évitera des branchements qui auraient été nécessaires sans cet apprentissage.
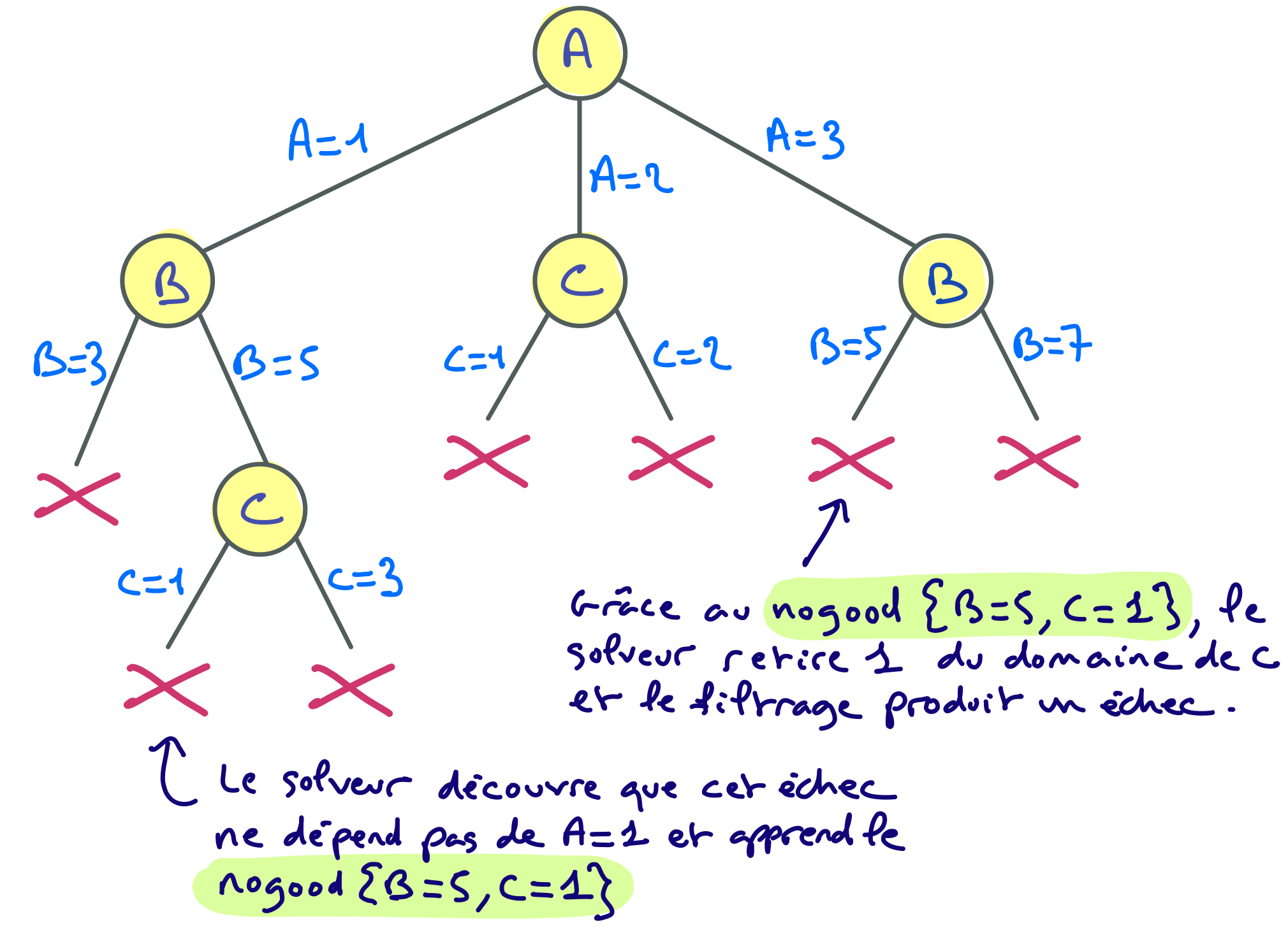
En pratique, les solveurs avec apprentissage sont très complexes et font généralement des redémarrages et des retours arrière non chronologiques, c’est-à-dire qu’après certains échecs et apprentissages associés, ils remontent plus haut que la dernière variable de branchement même si toutes les valeurs du domaine de cette variable n’ont pas été essayées.
Les nogoods ou autres connaissances qu’ils apprennent occupent un espace mémoire important, ce qui impose de retirer régulièrement certaines connaissances apprises. Malgré cette grande complexité, ces solveurs peuvent être beaucoup plus efficaces que les solveurs sans apprentissage (ou à apprentissage implicite). Par exemple pour problème SAT, dans lequel les contraintes sont des clauses en logique propositionnelle, les solveurs de type CDCL (pour Conflict Driven Clause Learning) qui apprennent (comme leur nom l’indique) de nouvelles clauses, pulvérisent les performances des solveurs énumératifs de type MAC (qui dans le contexte de SAT sont appelés DPLL d’après les initiales des noms des inventeurs).
D4 : Heuristiques de branchement
Le choix des variables de branchement (et des valeurs dans le cas de la version à branchement binaire) est critique pour l’efficacité des solveurs de type MAC. Sur des réseaux de quelques dizaines de variables, on peut facilement observer des rapports de temps d’exécution de l’ordre du milliard, ou beaucoup plus, selon la manière dont les variables de branchement sont choisies.
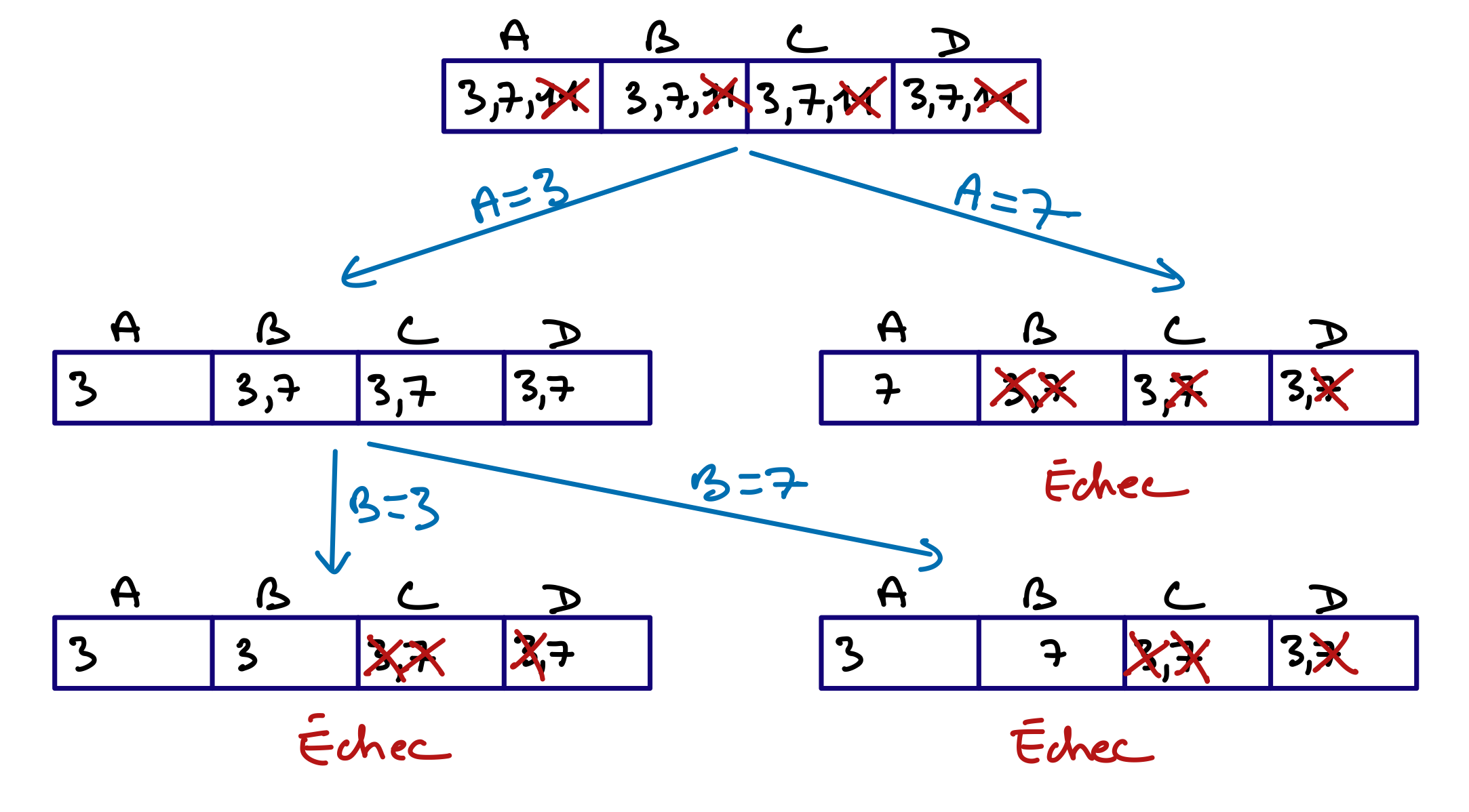
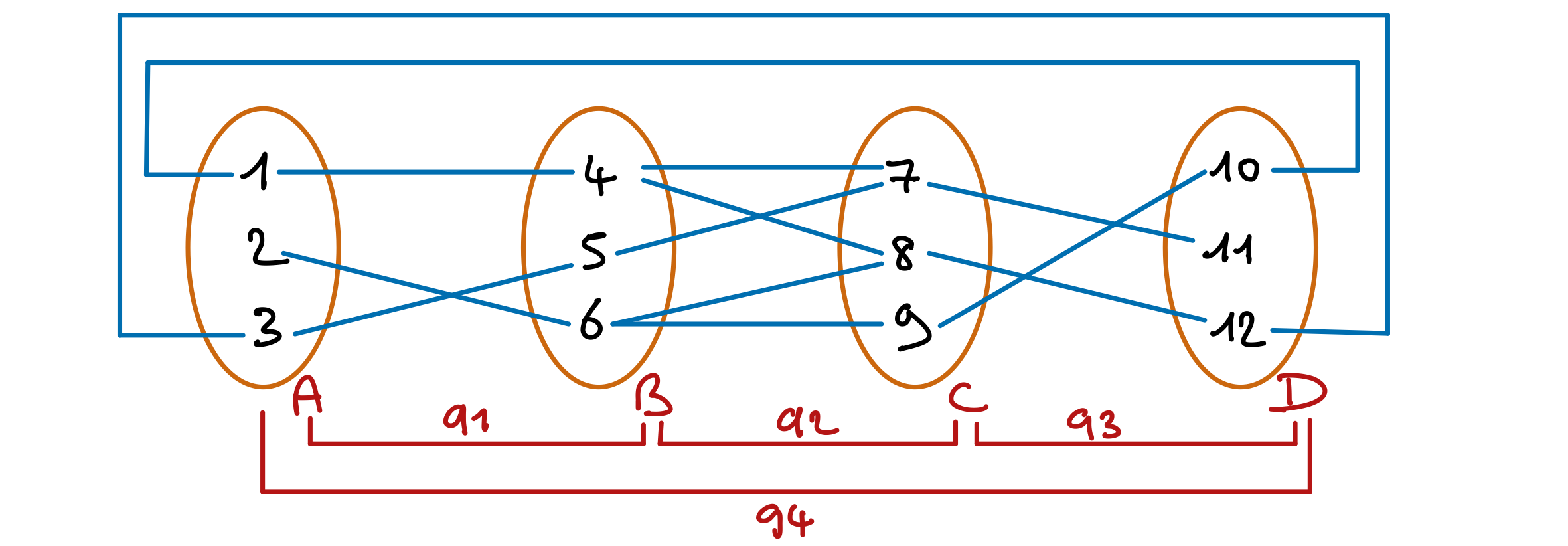
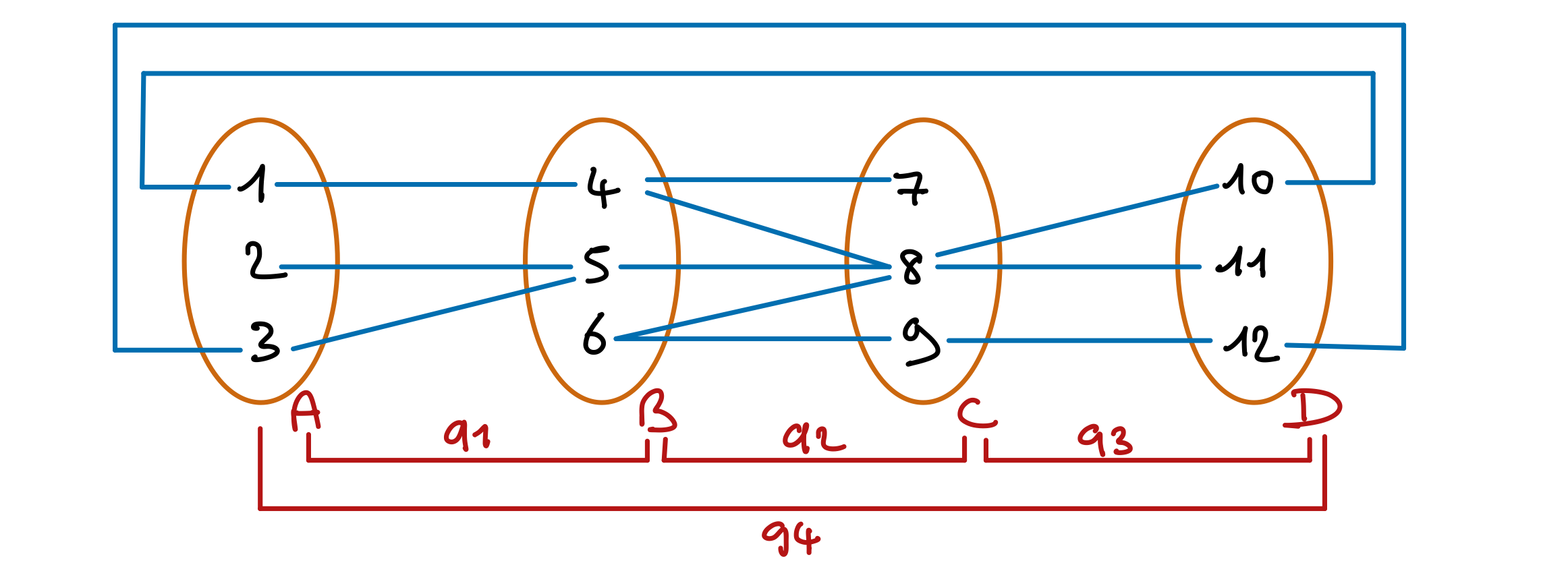
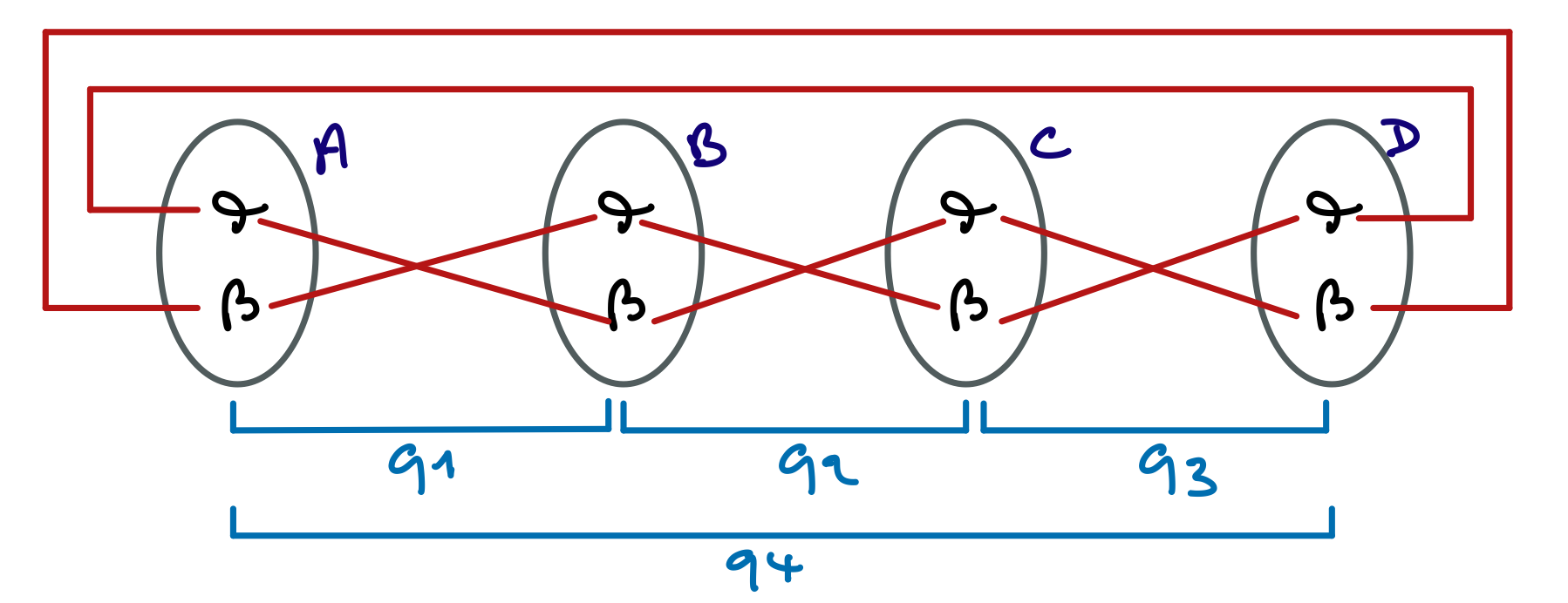
Pour comprendre l’importance de choisir les « bonnes » variable de branchement, considérons cet exemple.
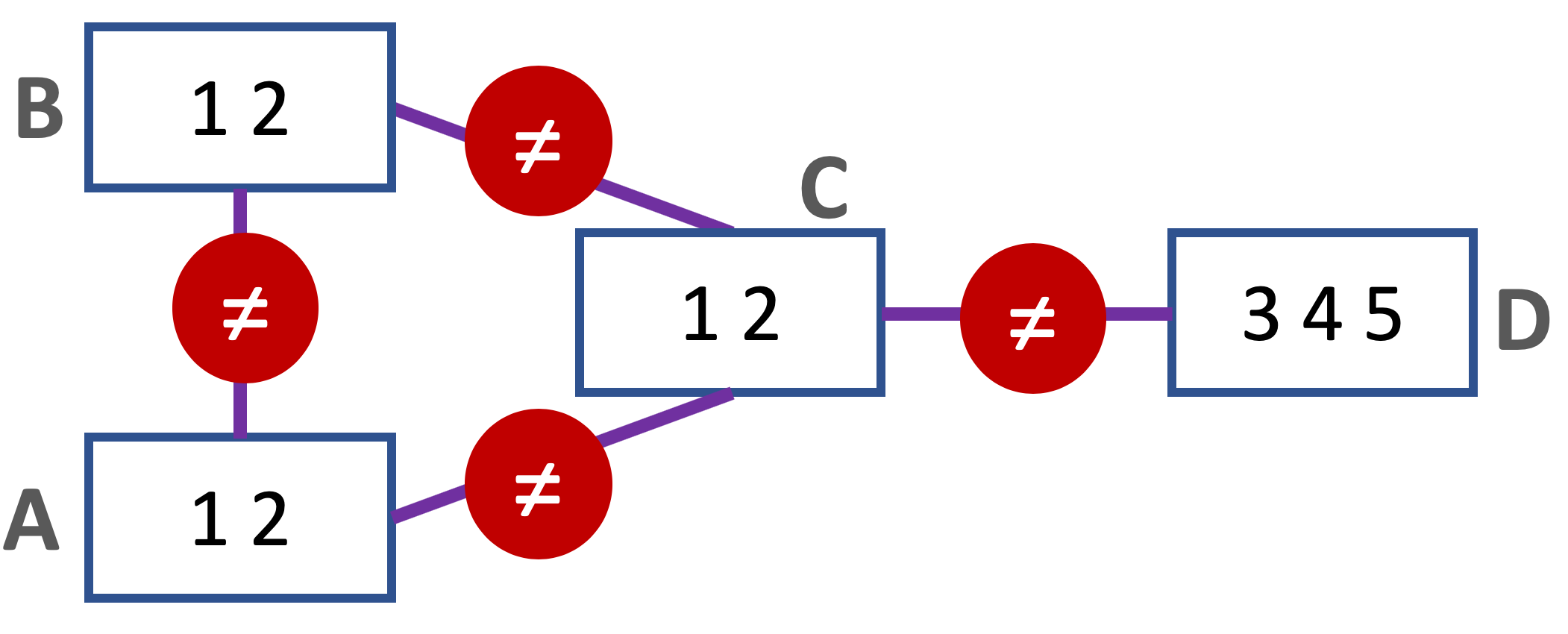
La cohérence de domaine est vérifiée pour toutes les contraintes. (Rappelez-vous que cette forme de cohérence ne considère qu’une seule contrainte à la fois !).
Si MAC commence par brancher avec une des variables A, B ou C, il déduira rapidement que le réseau est incohérent. Mais s’il commence par la variable D, il revérifiera trois fois l’incohérence du sous-réseau A, B, C.
Trouver la meilleure variable de branchement est (dans le cas général) plus difficile que résoudre le réseau, mais il existe des heuristiques de choix de la variable de branchement qui sont plus ou moins efficaces selon la nature des contraintes et la structure du réseau.
On appelle heuristique un critère de choix facile à calculer (qui prend un temps faible au regard des autres traitement réalisé par le solveur) mais qui ne donne aucune garantie d’optimalité.
Ces heuristiques peuvent prendre en compte, par exemple :
-
la taille du domaine de chaque variable,
-
le nombre de contraintes dans lesquelles chaque variable intervient,
-
le nombre d’assignations partielles autorisées par chaque contraintes,
-
des poids attribués à chaque variable, qui évoluent au cours de la recherche en fonction de l’efficacité des filtrages réalisés sur leurs domaines (on parle alors d’heuristiques dynamiques)…
C’est un très vaste sujet que nous n’approfondirons pas ici. Même lorsque le réseau de contraintes est cohérent, c’est le choix des variables de branchement qui est particulièrement critique pour trouver une solution. Bien évidemment, si on pouvait « deviner » les assignations des variables d’une solution, on la trouverait immédiatement quelles que soient les variables de branchement. Mais en pratique il s’avère souvent que « deviner » les solutions à l’aide d’une heuristique ne fonctionne pas, alors que les heuristiques efficaces pour prouver l’incohérence du réseau de contraintes sont celles qui sont également les plus efficaces pour trouver des solutions lorsque le réseau de contraintes est cohérent.
Exercices d’assimilation
D-ass-01
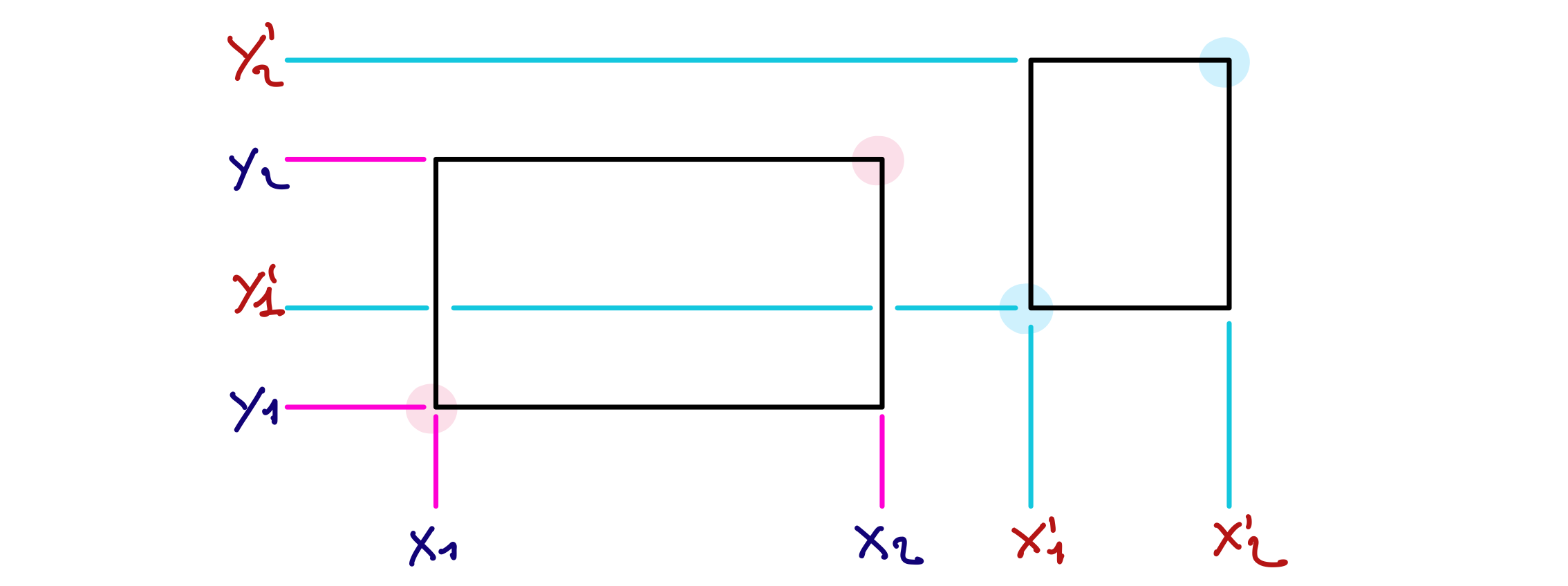
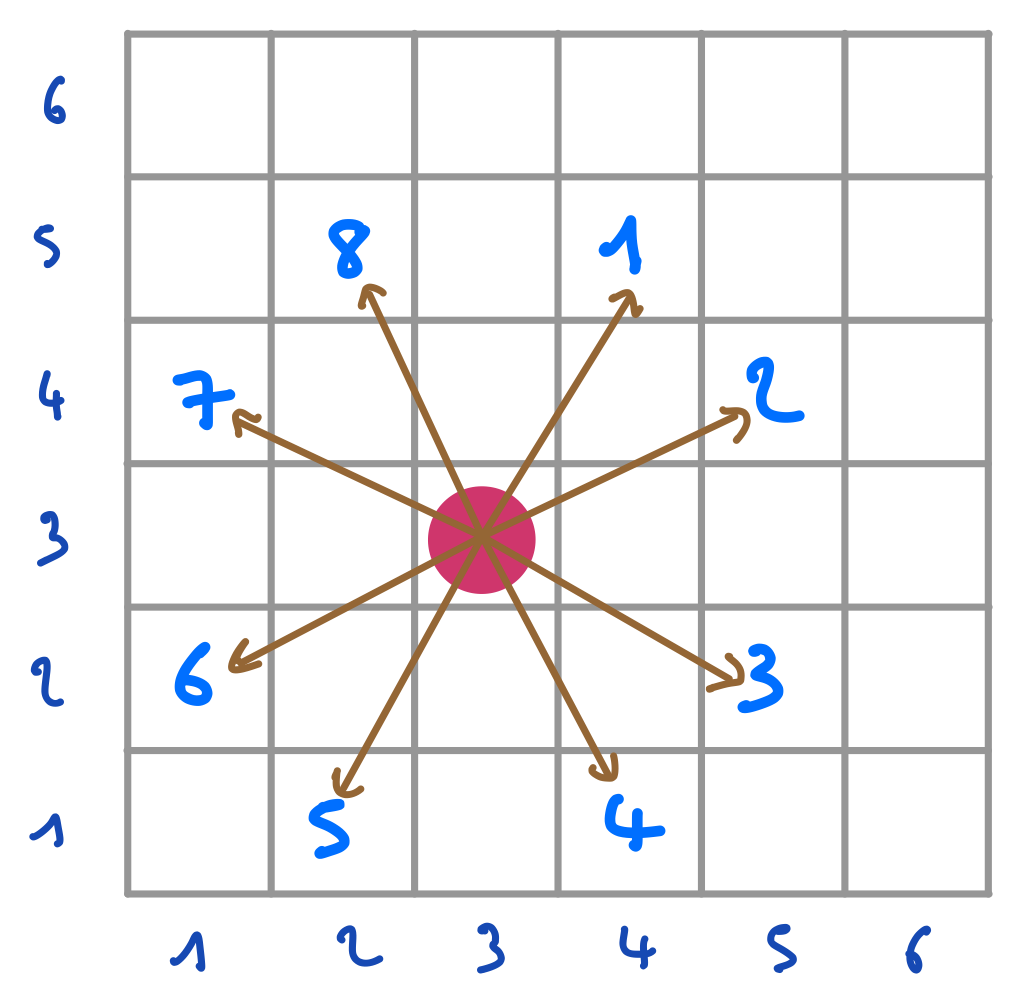
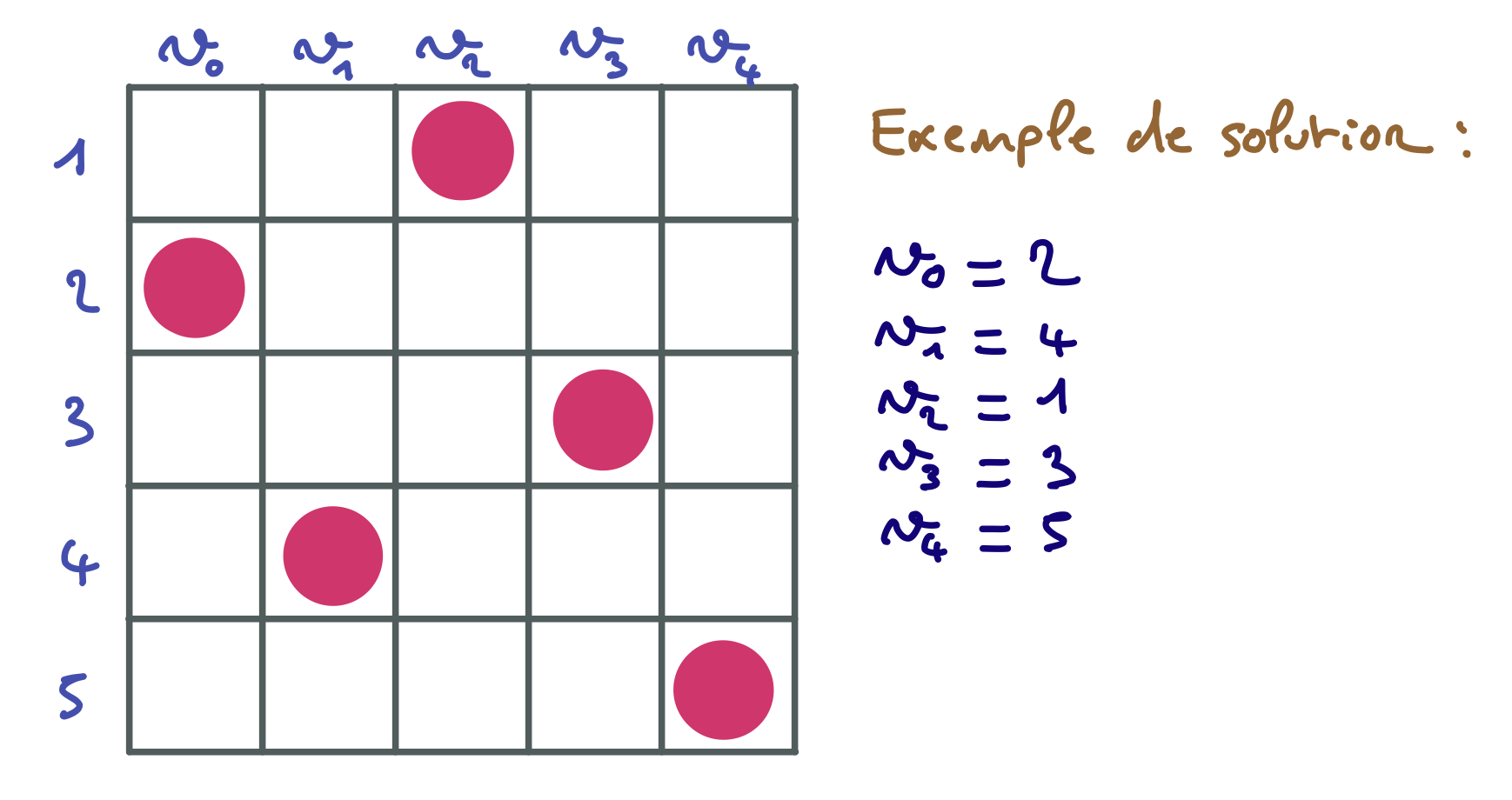
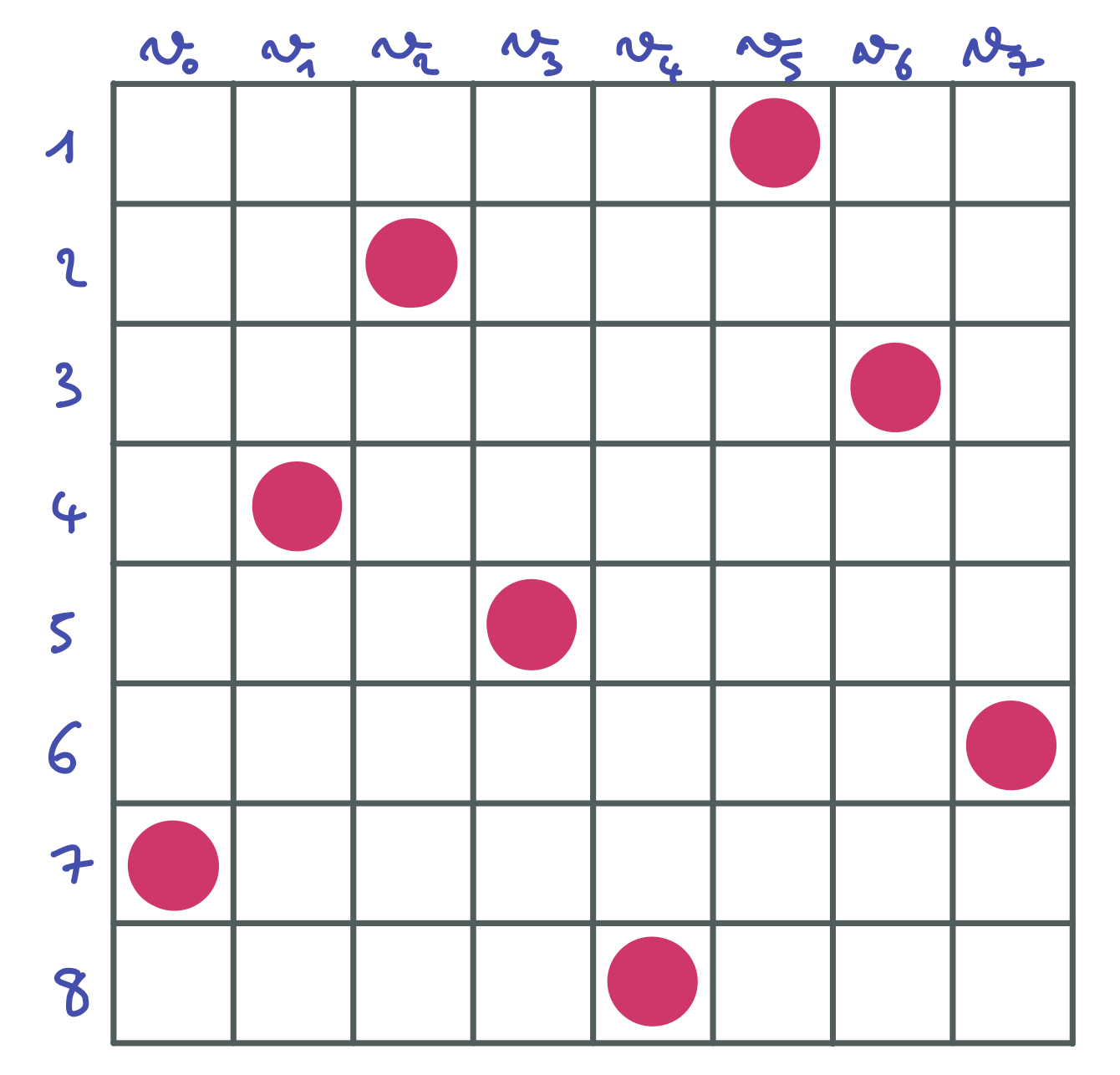
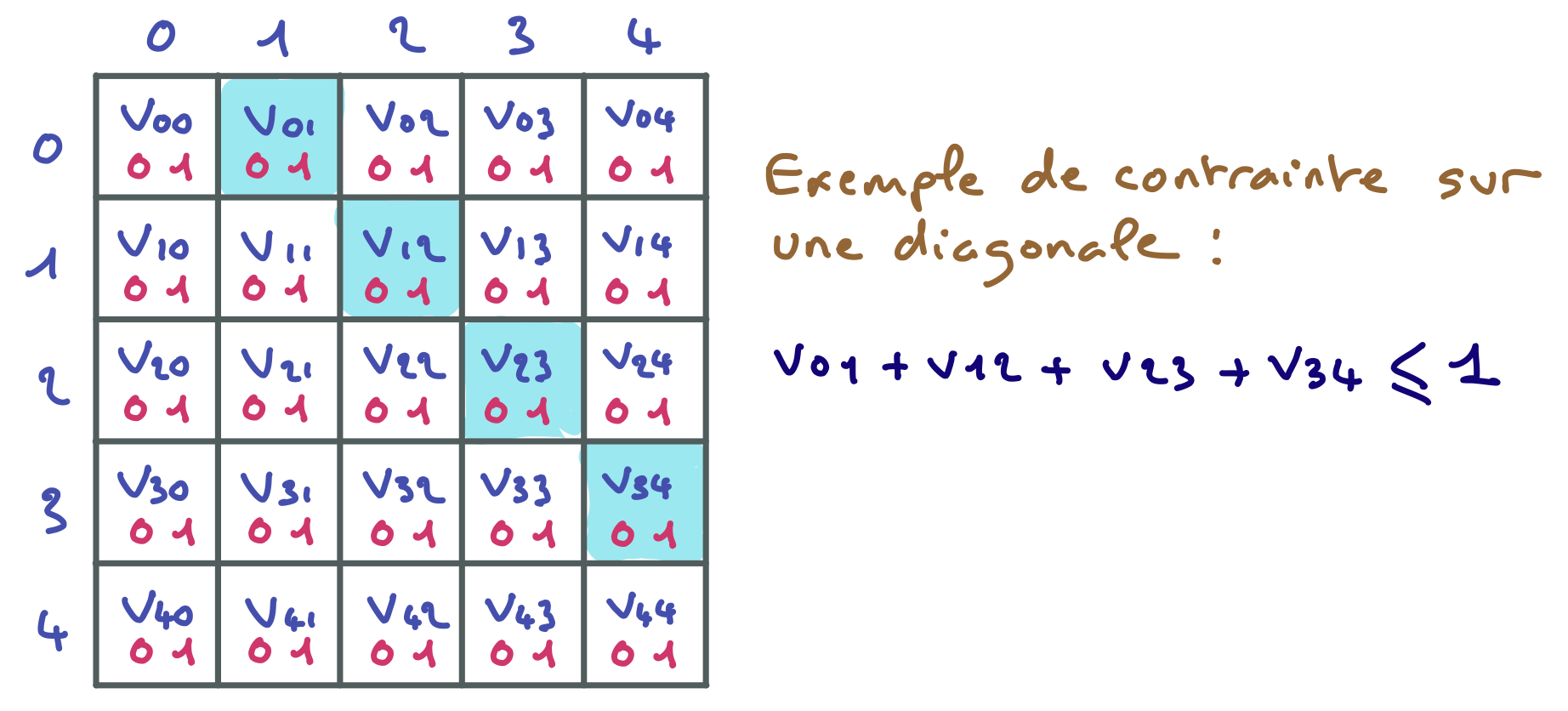
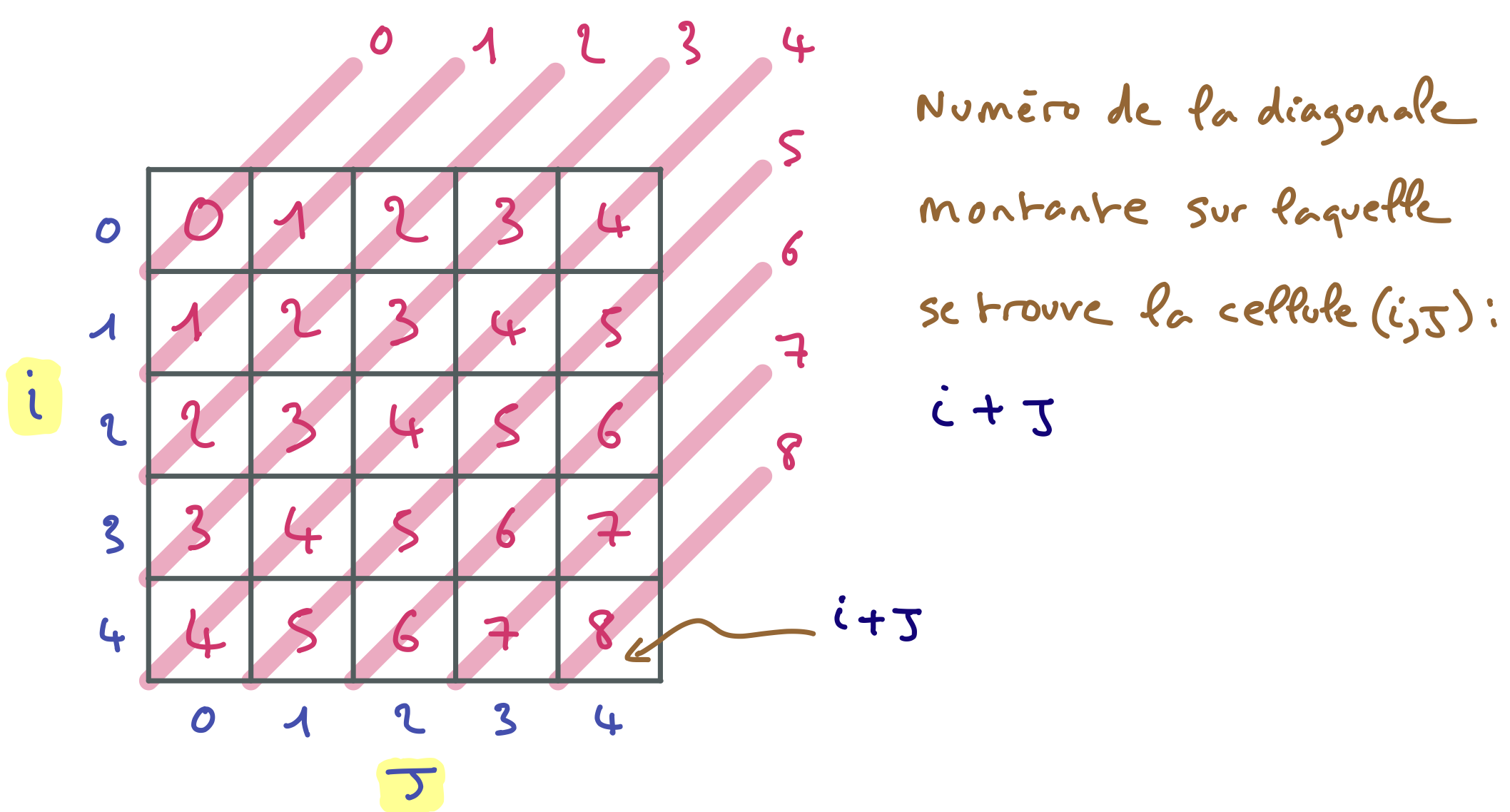
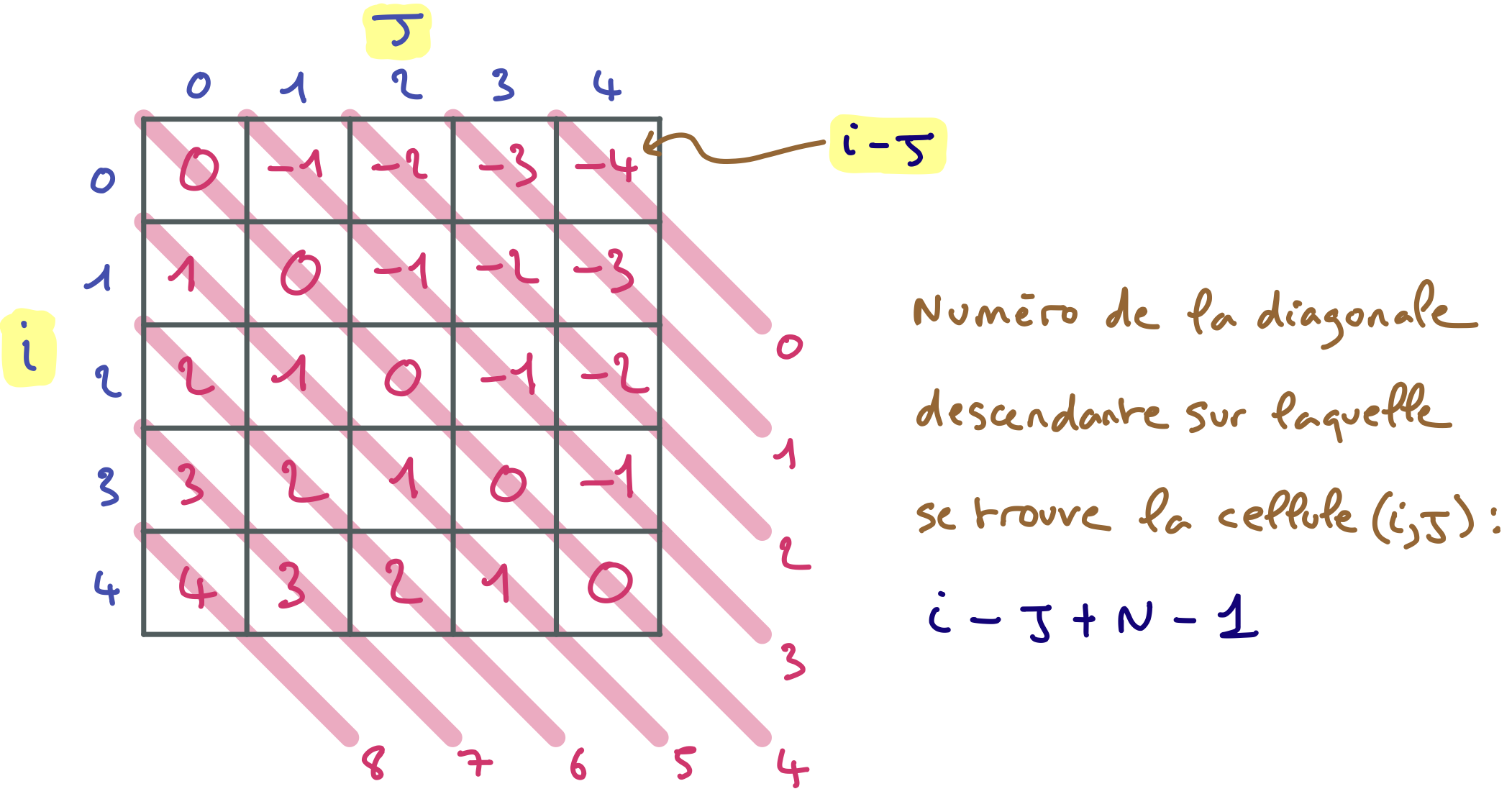
Complétez cet arbre de recherche de l’algorithme MAC sur le problème des 5 reines. Chaque pastille ronde rose représente l’assignation d’une variable de branchement. Les croix grises représentent les valeurs des domaines des variables qui ont été filtrées (ou éliminées du fait de l’assignation de la variable). Les pastilles carrées roses représentent les valeurs assignées par filtrage (quand il ne reste qu’une valeur dans le domaine concerné). On considère qu’il y a 10 contraintes reliant respectivement A et B, A et C, A et D, A et E, B et C, B et D, B et E, C et D, C et E, D et E. Chacune de ces contraintes exprime que les reines situées sur les colonnes associées aux variables concernées ne sont ni sur une même ligne, ni sur une même diagonale.
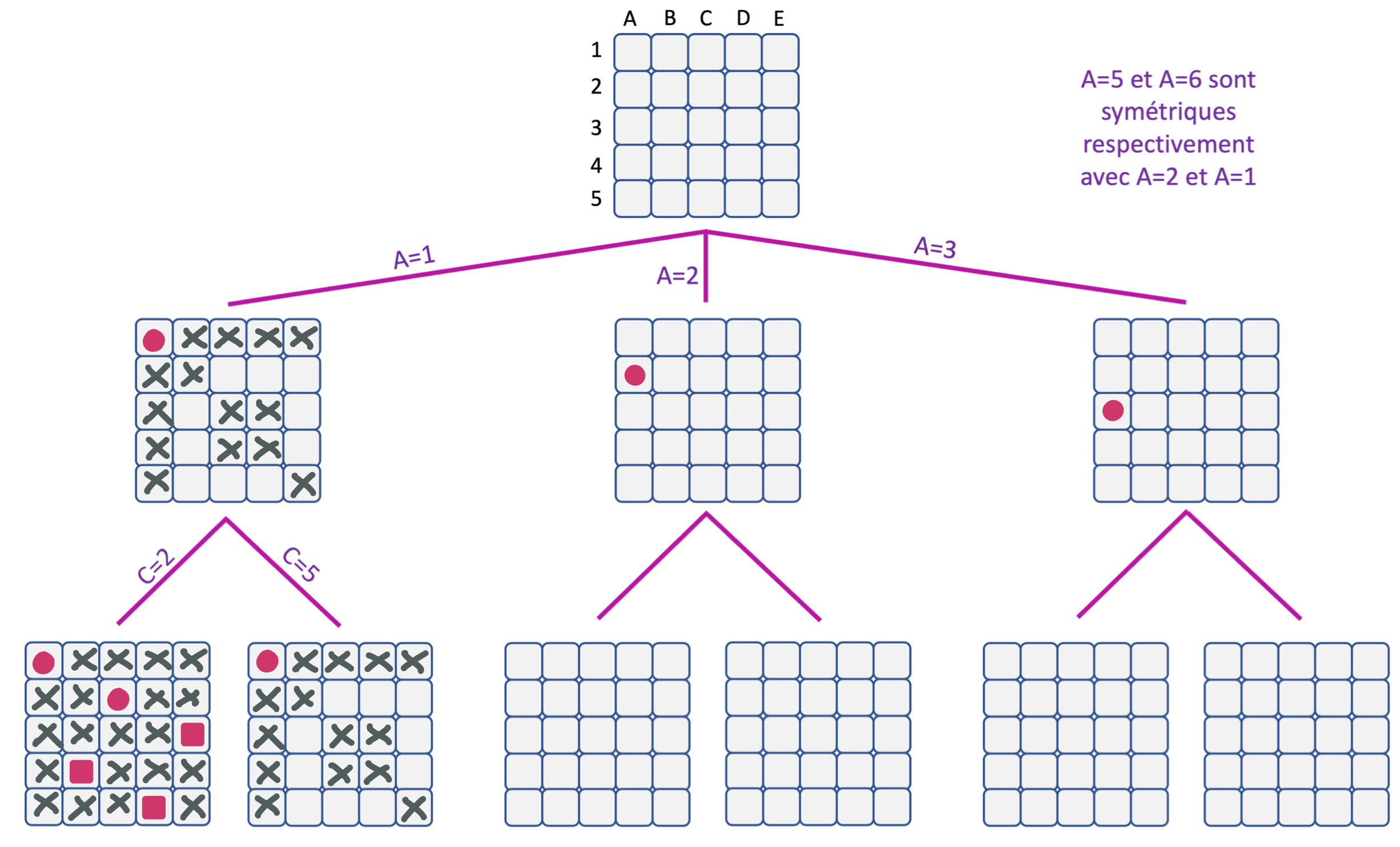
"Indice1"
Tout d’abord, il faut que vous soyez convaincu du résultat du filtrage pour $A = 1$. Les croix apparaissant sur la figure de gauche sont assez évidentes, puis qu’elles correspondent à des valeurs des variables B, C, D, E qui représentent des reines positionnées sur une même ligne ou une même diagonale que la reine représentée par A=1. Par exemple, il y a une croix pour C=3 parce-que C=3 n’a pas de support pour la contrainte entre A et C, parce que si on avait A=1 et C=3, cela reviendrait à mettre les reines des colonnes A et C sur une même diagonale.
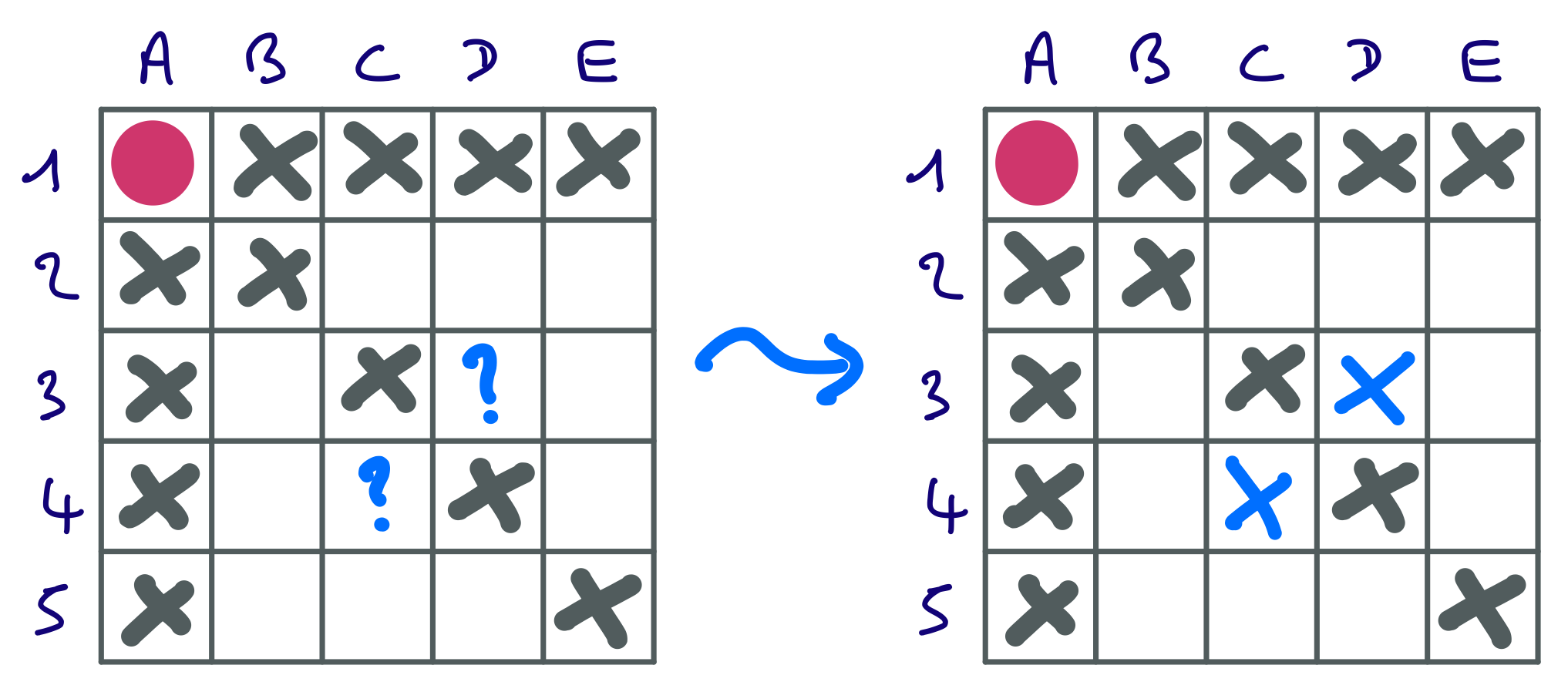
Mais pourquoi faut-il aussi mettre des croix pour C=4 et D=3 ? N’oubliez pas que vous devez continuer le filtrage tant qu’il reste dans certains domaines des valeurs n’ayant pas de support pour certaines contraintes.
Or C=4 n’a pas de support pour la contrainte entre B et C ! En effet, le domaine de B est {3,4,5} (les valeurs non barrées dans la colonne B. Si on assignait C=4, on ne pourrait pas assigner B=3 (conflit diagonale), ni B=4 (conflit ligne), ni B=5 (conflit diagonale). Donc aucune des valeurs du domaine de B n’est compatible avec C=4 au regard de la contrainte entre B et C. On doit donc retirer C=4.
Un raisonnement similaire pour la contrainte entre D et E permet de supprimer D=3, d’où les deux croix en C=4 et D=3. Quels sont les filtrages supplémentaires à ajouter si on assigne C=5 ? Trouvez les vous-même avant de consulter la réponse au prochain indice.
"Indice2"
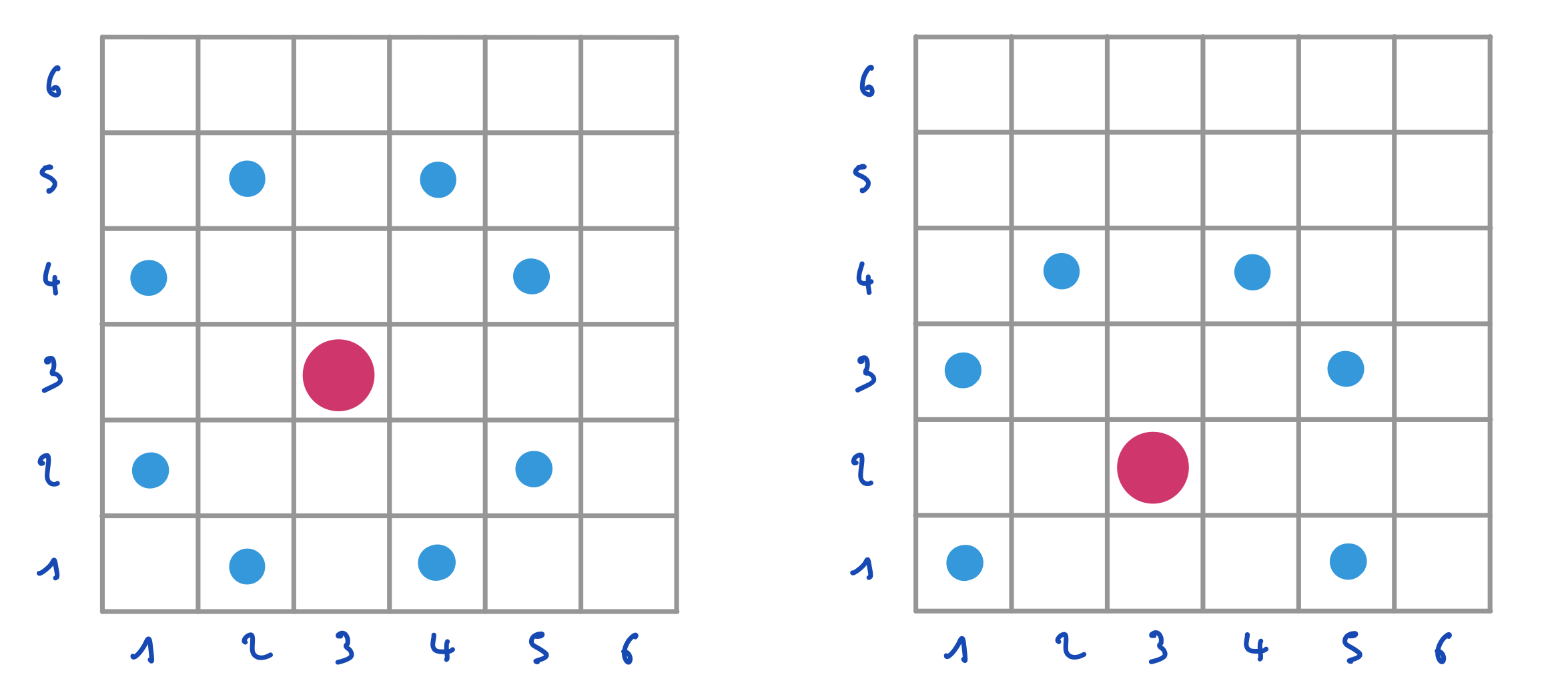
Sur cette figure, le filtrage pour la branche A=1, C=5 a été terminé et a donné lieu à une solution. Le filtrage pour A=2 a été réalisé. Merci de continuer avec la variable de branchement C.
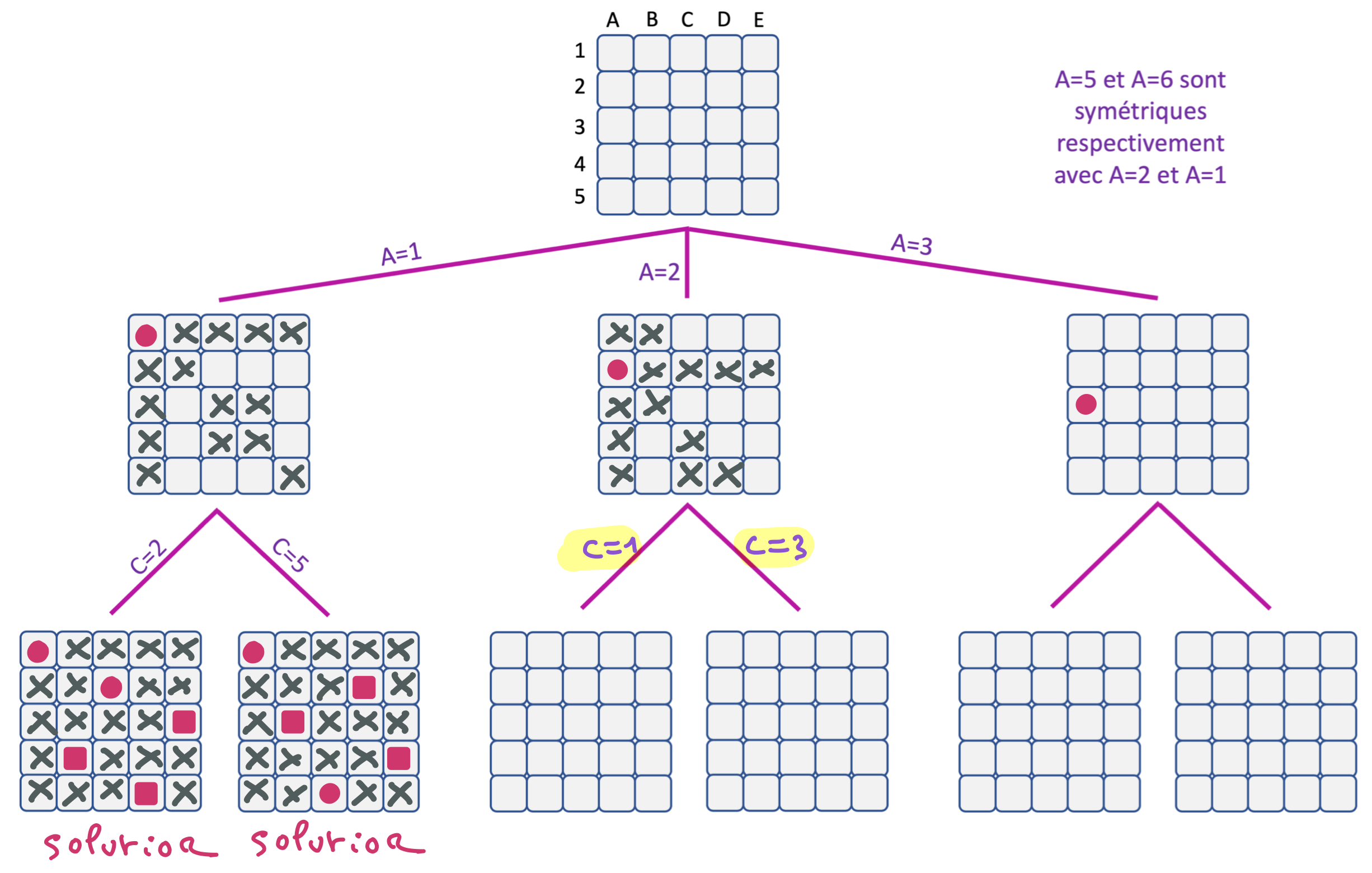
"Indice3"
Les branchements C=1 et C=3 après A=2 produisent chacun une solution par filtrage. A vous de tenter de terminer l’arbre de recherche avant de consulter le dernier indice.
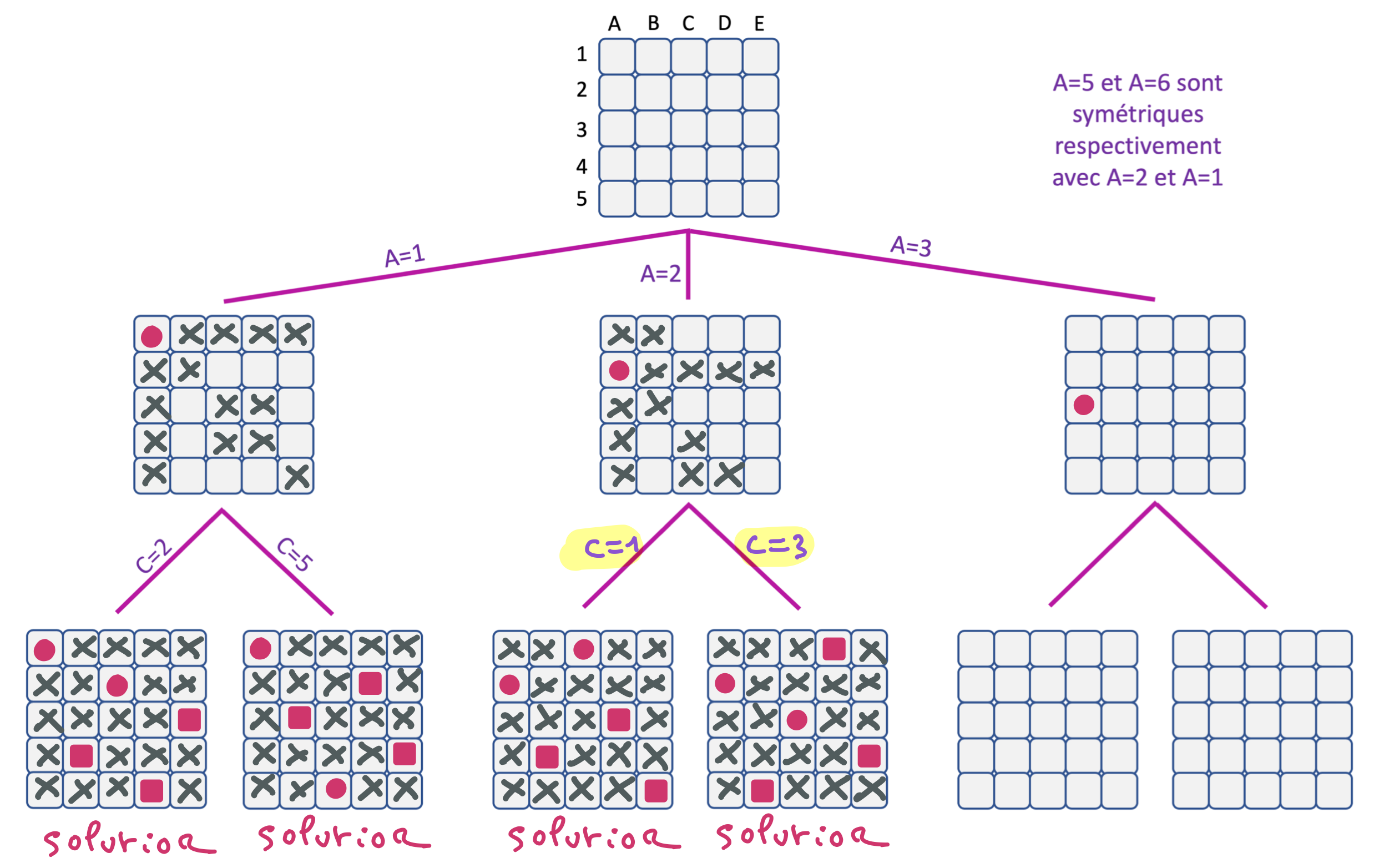
"Solution"
Voici le développement complet des branches A=1, A=2, A=3.
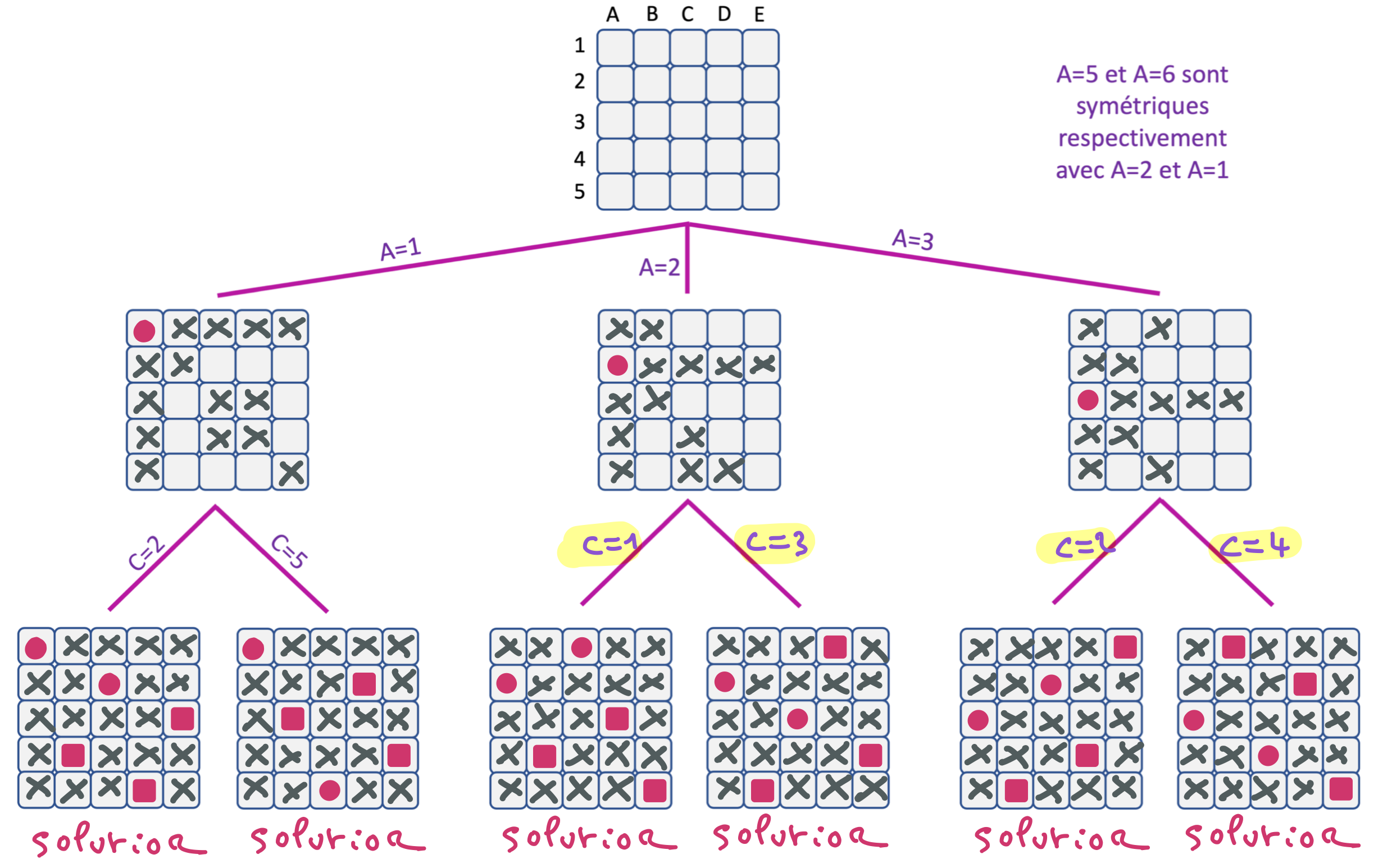
Comme les branches A=4 et A=5 sont symétriques avec les branches A=2 et A=1 (bien que peu de solveurs soient capables de le prendre en compte), on en déduit que le problème des 5 reines a 10 solutions.
D-ass-02
Soit le problème suivant :
Variables :
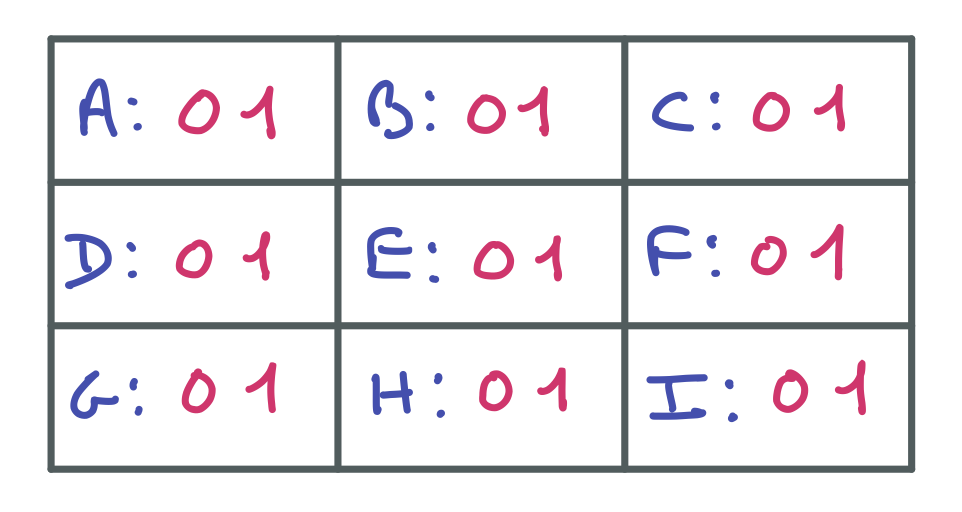
Contraintes :
Pour chaque ligne et chaque colonne, une contrainte exprime que la somme des variables concernées vaut 2. $A + B + C = 2$, $D + E + F = 2$, $G + H + I = 2$, $A + D + G = 2$,$B + E + H = 2$, $C + F + I = 2$.
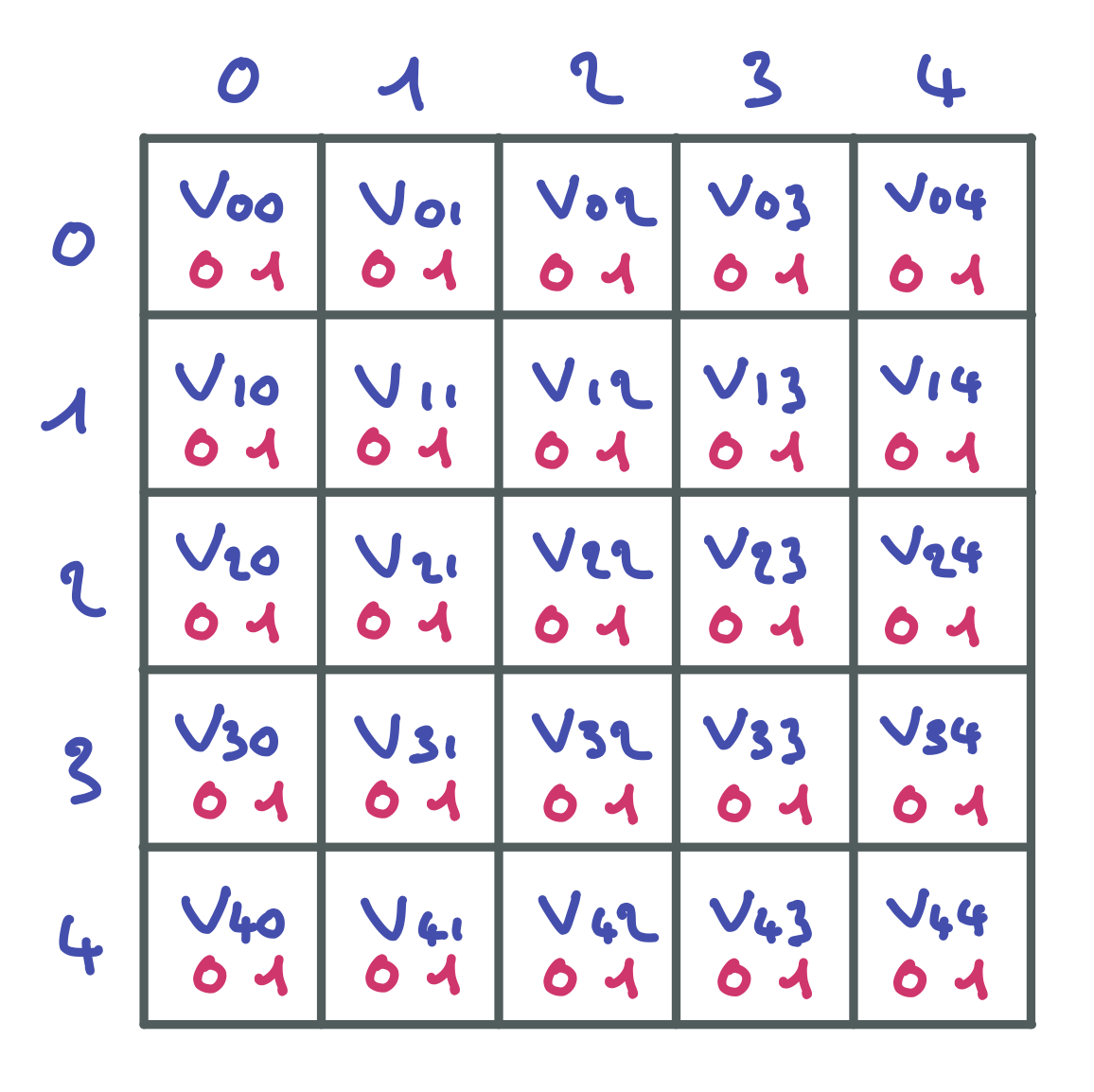
Réalisez une simulation de l’exécution d’un solveur MAC sur cette instance de problème. Dessinez l’arbre de recherche complet (recherchant toutes les solutions), en précisant à chaque nœud les domaines des différentes variables. Pour faciliter la lecture, merci de représenter ces domaines sous la forme d’une grille de 3 par 3 avec la convention suivante : une case blanche représente le domaine {0,1} , une case contenant la valeur 0 représente le domaine {0} , et une case contenant la valeur 1 représente le domaine {1}.
"Indice1"
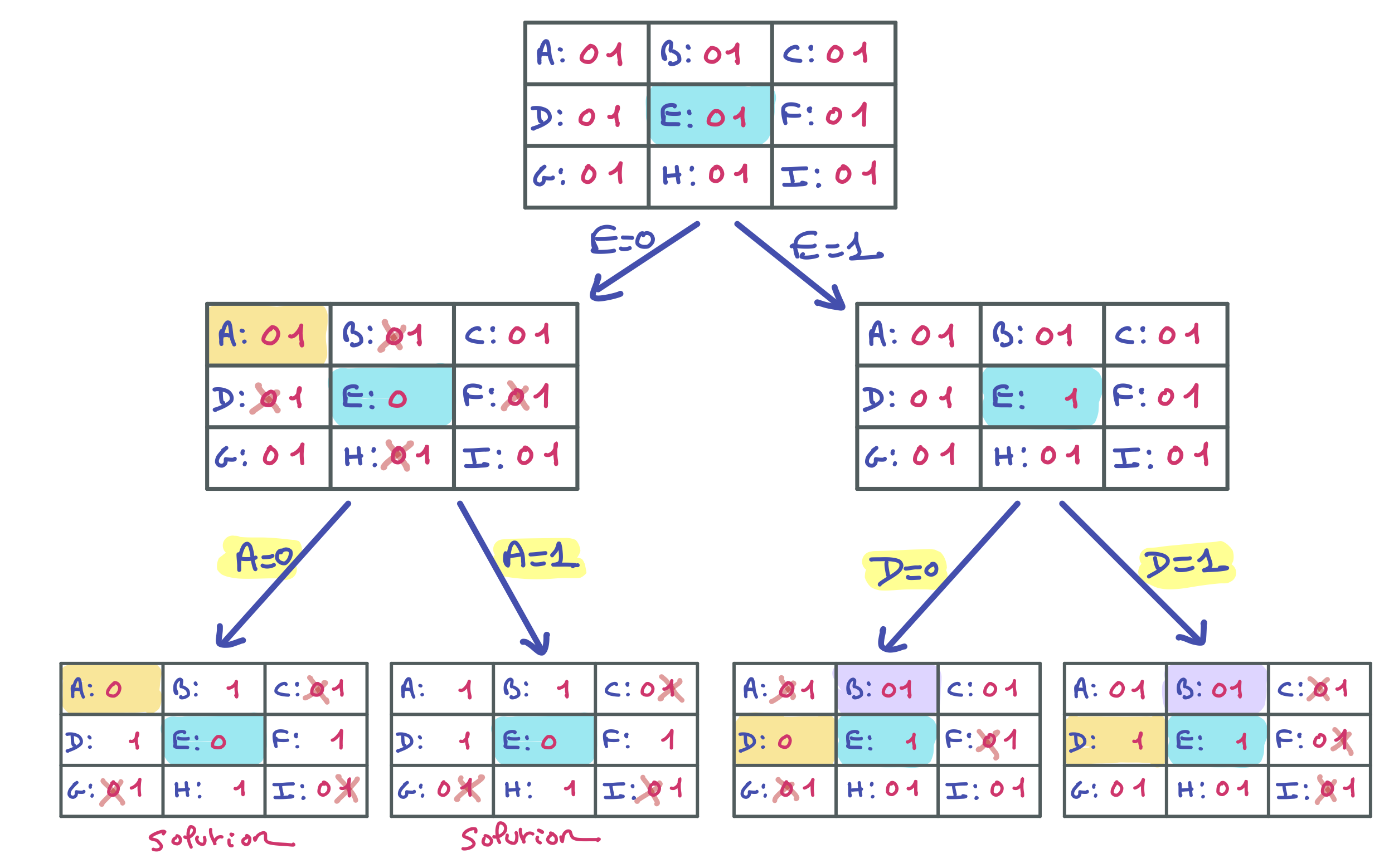
Voici le premier niveau de l’arbre de recherche en choisissant E comme variable de branchement. Ce n’est pas obligatoire, mais les indices suivants seront basés sur ce choix.
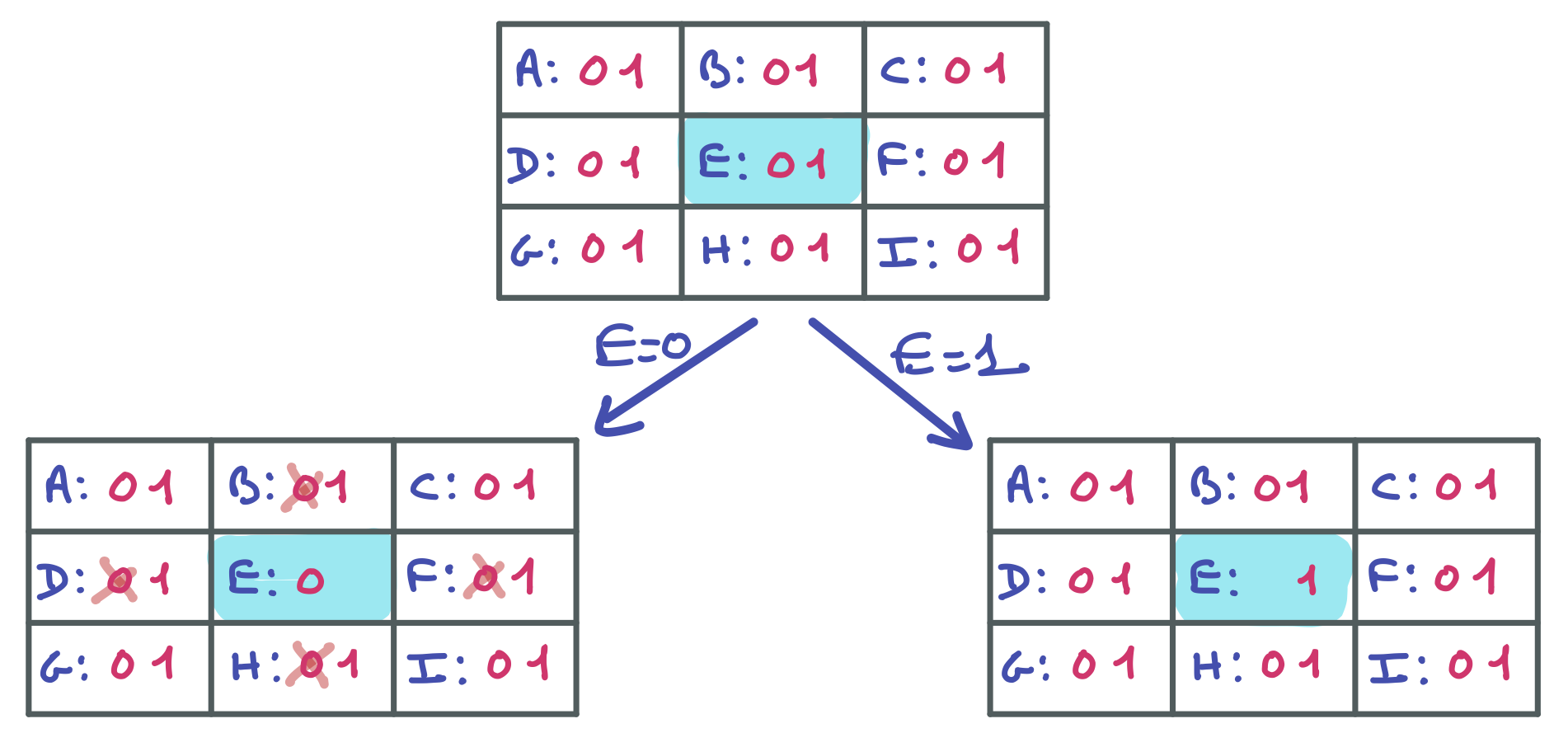
On voit que le côté gauche filtre un peu, alors que le côté droit ne filtre pas, mais cela aurait été la même chose avec tout autre choix de la variable de branchement.
"Indice2"
La branche gauche aboutit à deux solutions en branchant sur A, par exemple. Le prochain indice sera basé sur un branchement sur D à droite.
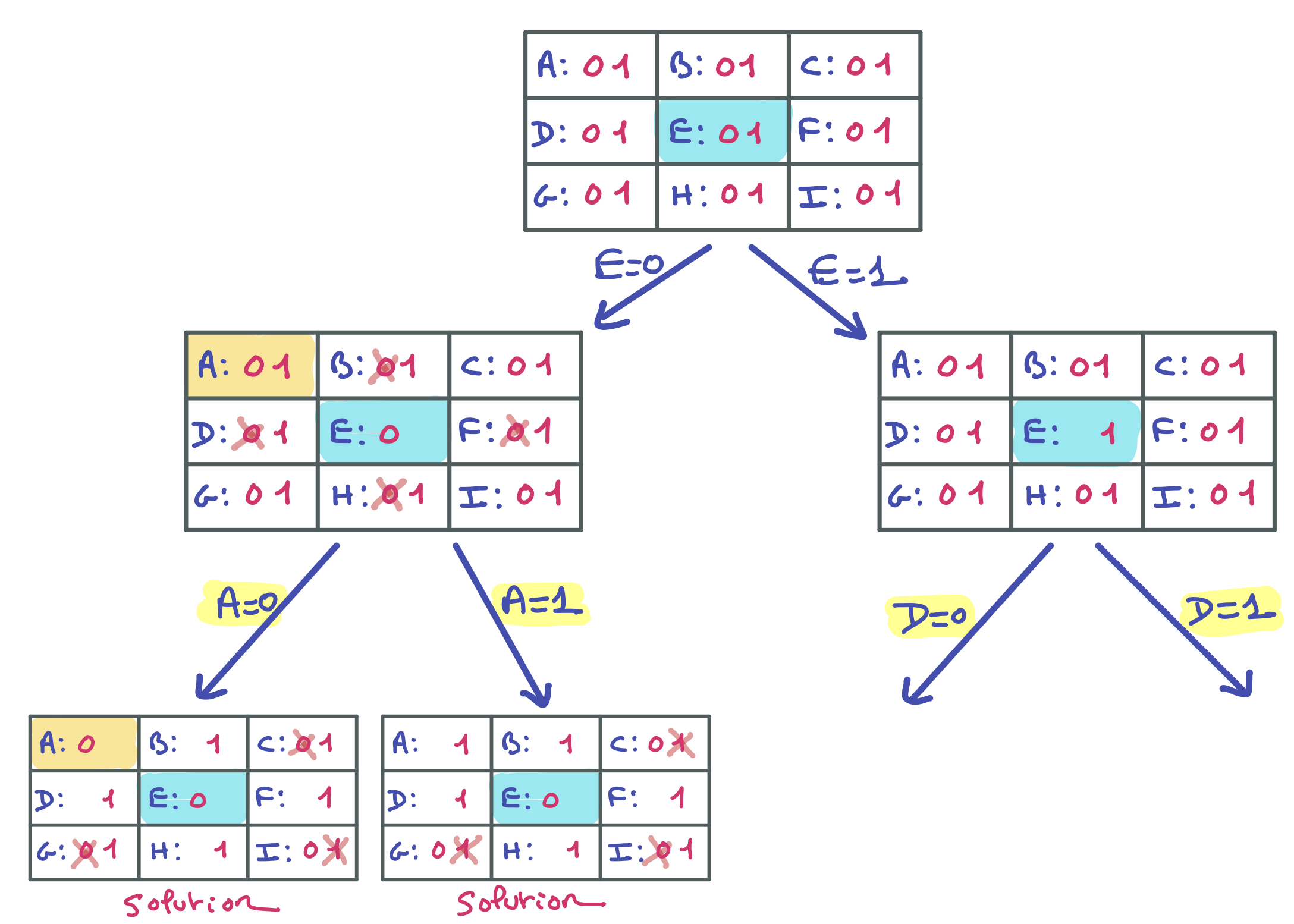
"Indice3"
Voici le développement de tout le deuxième niveau. Pour la suite, E est la variable de branchement préconisée.
"Solution"
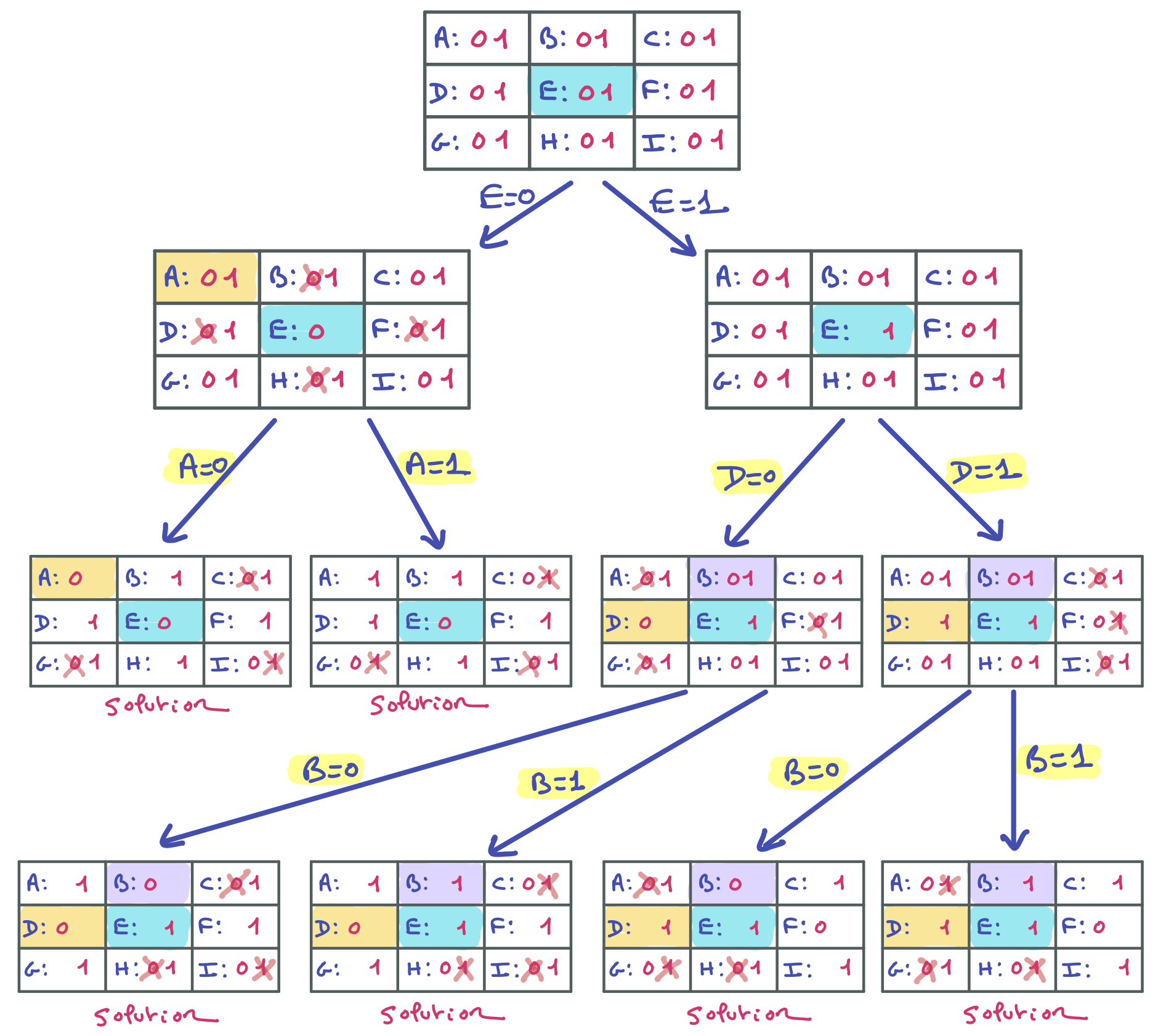
Voici l’arbre de résolution complet, qui fait apparaitre les 6 solutions du réseau. Étant donné qu’il y a 6 solutions, quelles que soit les choix des variables de branchement, l’arbre de recherche aura au moins 6 branches, donc 5 nœuds binaires. Il n’existe donc pas de stratégie de branchement produisant un arbre plus petit.
D-ass-03
Soit le réseau de contraintes suivant :
-
Variables : A avec domaine {0,5}, B avec domaine {0,6}, C avec domaine {0,9}, D avec domaine {0,2}.
-
Contraintes : A + B + C + D >= 15 et A + B + C + D <= 15.
Détaillez la résolution de ce problème par l’algorithme MAC (Maintaining Arc Consistency). Choisissez les variables de branchement de manière à minimiser la taille de l’arbre de recherche.
"Indice1"
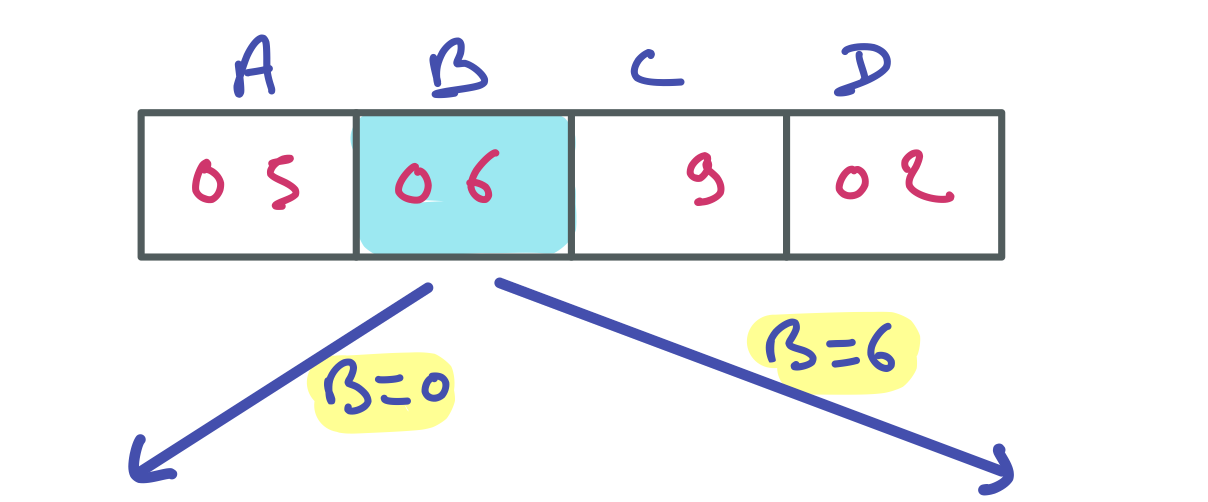
La première chose à faire est de rétablir la cohérence de domaine, si applicable. Or il y a bien une valeur à enlever. C=0 n’a pas de support pour la contrainte A + B + C + D >= 15. C’est le seul filtrage possible, donc pour continuer il faut choisir une variable de branchement. Pourquoi pas B ?
"Indice2"
Avec B=0, A=0 et D=0 ne peuvent satisfaire la contrainte A + B + C + D = 15. Les valeurs 0 sont donc retirées des domaines de A et D. Mais alors, aucune des valeurs restant dans les domaines ne permet de satisfaire la contrainte A + B + C + D <= 15.
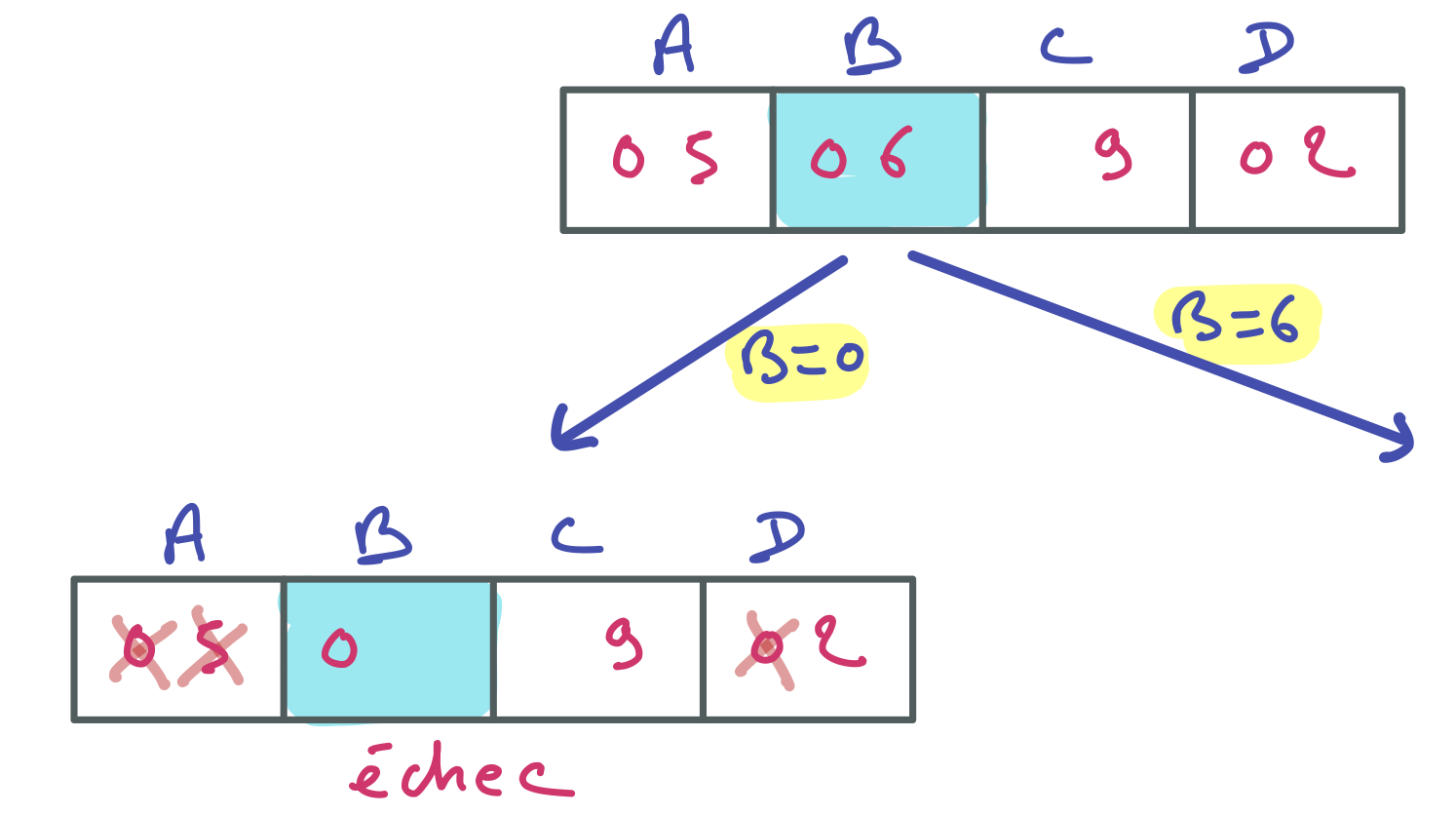
Pour la forme, on matérialise l’incohérence en retirant 5 du domaine de A, mais on aurait pu vider tout autre domaine, puisque les valeurs restantes, par définition, n’ont pas de support pour A + B + C + D <= 15.
Il reste un espoir de trouver une solution avec la branche B=6…
"Solution"
Voici l’arbre de recherche complet. Le filtrage des domaines de A et D au regard de la contrainte A + B + C + D >= 15 permet de retirer les valeurs non nulles et de produire une solution.
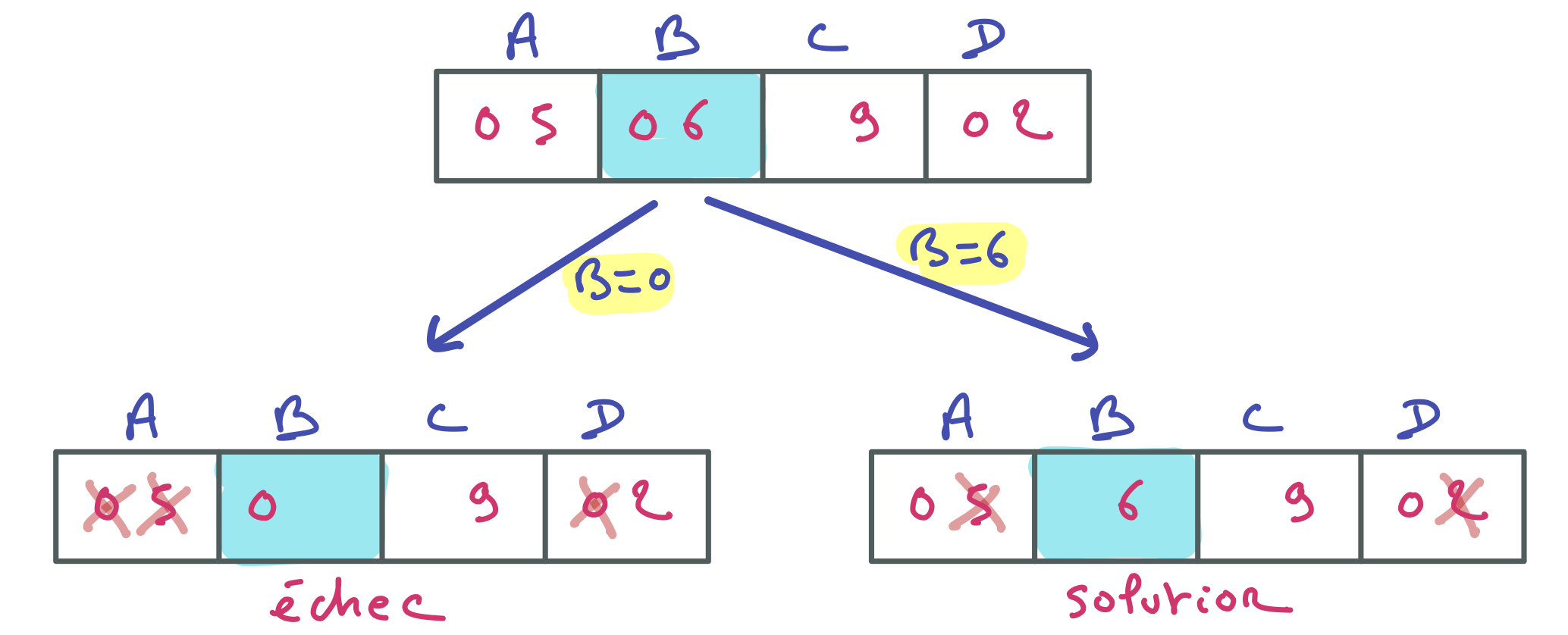
D-ass-04
Soit le réseau constitué des 6 contraintes logiques suivantes, appelées clauses.
$$(a \vee b), (\neg a \vee b), (a \vee \neg b), (\neg a \vee \neg b \vee c), (\neg c \vee d), (\neg c \vee \neg d)$$
Les variables ont toutes pour domaine {0,1}.
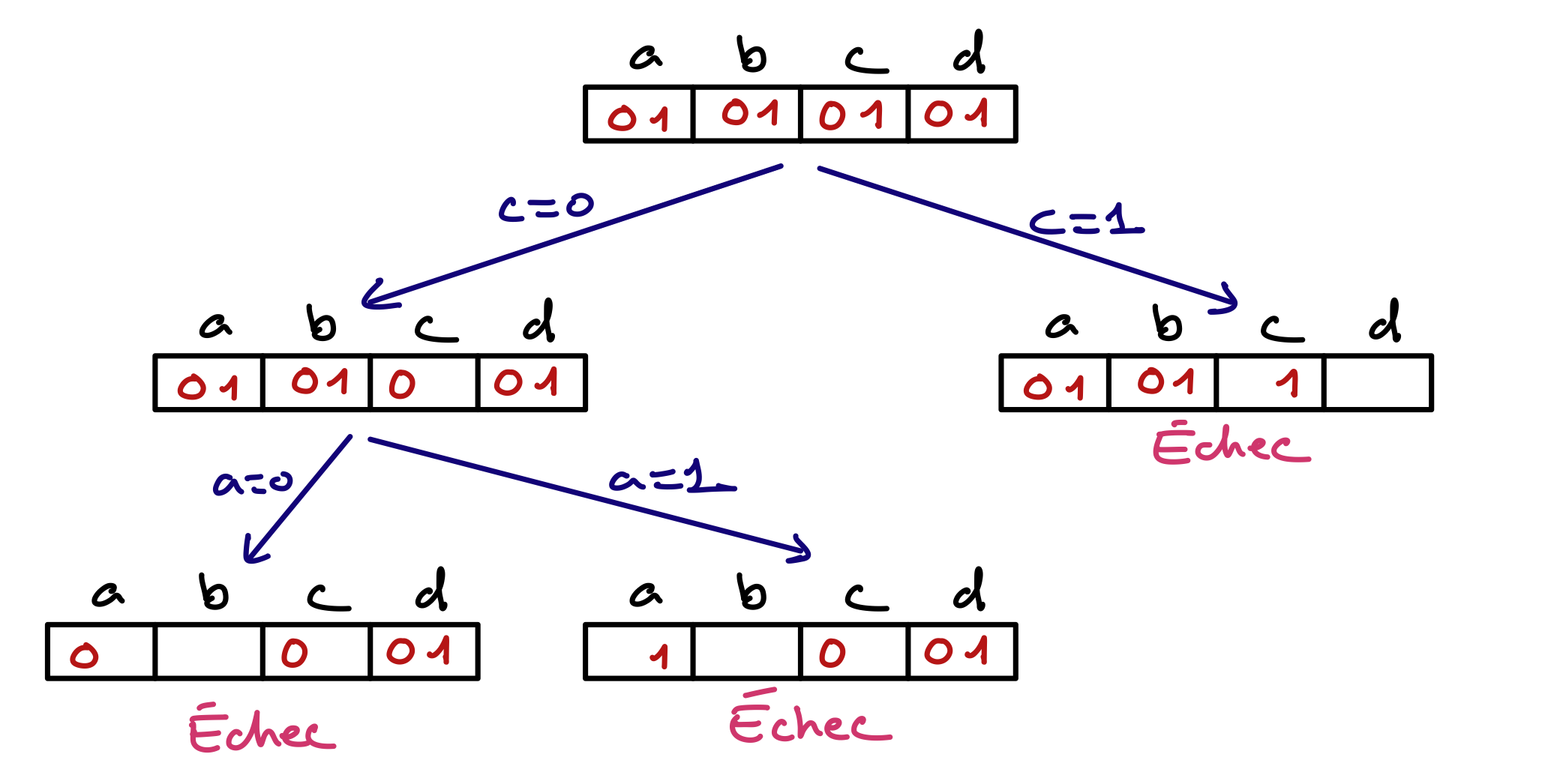
Détaillez la résolution de ce problème par l’algorithme MAC. A chaque nœud ou feuille, redonnez les domaines en barrant les valeurs éliminées par filtrage ou par assignation de la variable de branchement. A chaque feuille, précisez s’il y a échec ou solution. Essayez de choisir les variables de branchement de manière à minimiser la taille de l’arbre de recherche.
"Indice1"
Tout d’abord il faut restaurer la cohérence de domaine. Mais il n’y a aucun filtrage possible avec les domaines initiaux. Chaque clause fait intervenir plusieurs variables et quelle que soit la valeur d’une de ces variables, il existe toujours au moins une valeur pour l’autre qui permet de satisfaire la clause.
Pour la suite, merci d’utiliser la variable $a$ comme variable debranchement.
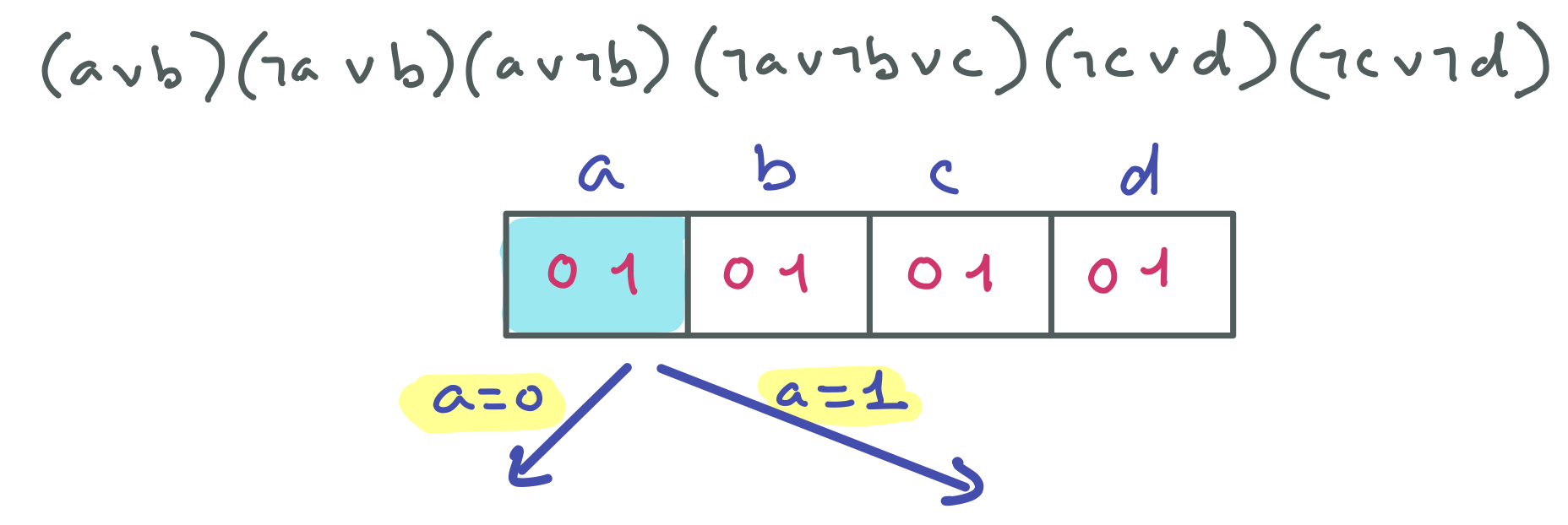
"Indice2"
Avec $a = 0$, $b = 0$ n’a pas de support pour la clause $(a \vee b)$ et $b = 1$ n’a pas de support pour la clause $(\neg a \vee b)$.
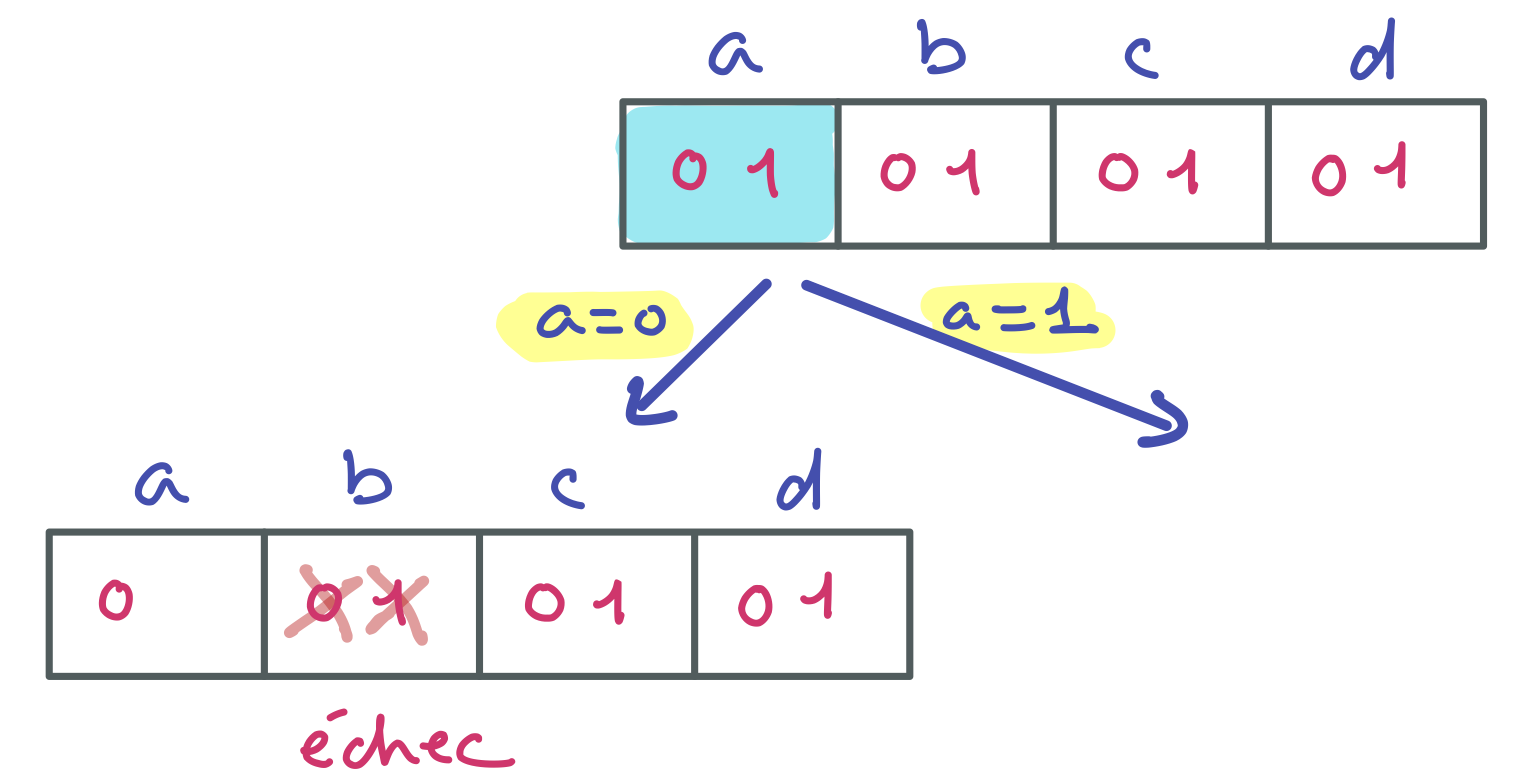
Avec les clauses, on peut raisonner directement sur les contraintes en barrant les littéraux qui sont falsifiés par les assignations déjà réalisées.
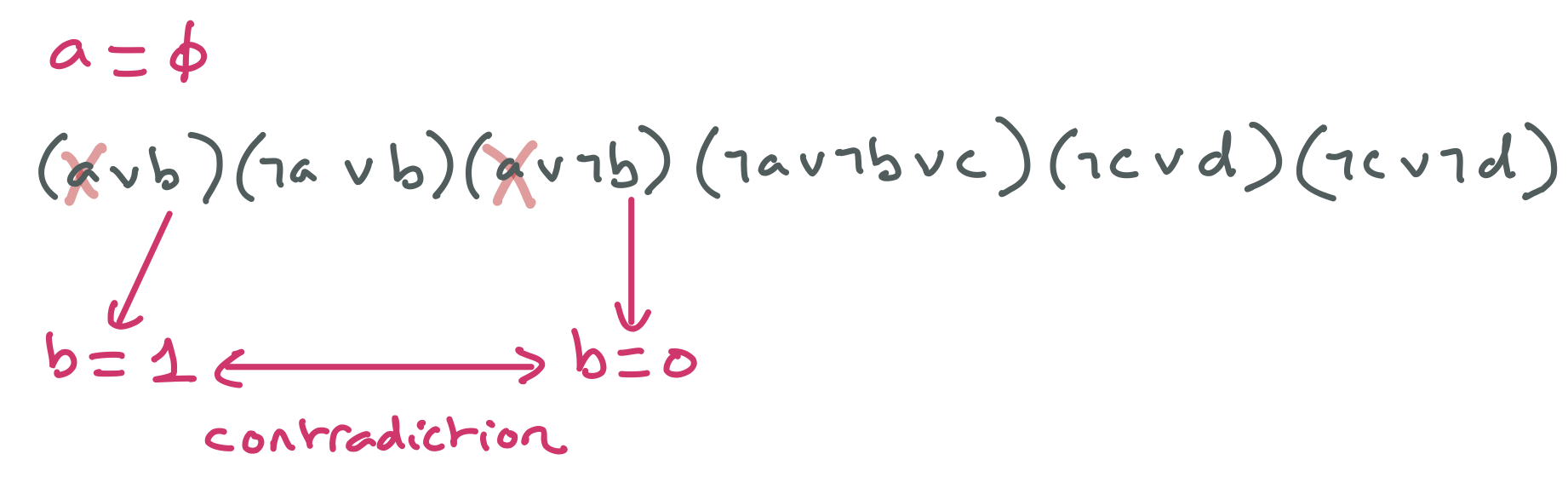
Quand il reste un seul littéral dans une clause, cela impose une assignation de la variable concernée. Dans le contexte du problème SAT, c’est-à-dire quand toutes les contraintes sont des clauses, cette technique est appelée propagation unitaire.
"Solution"
Voici l’arbre de résolution complet.
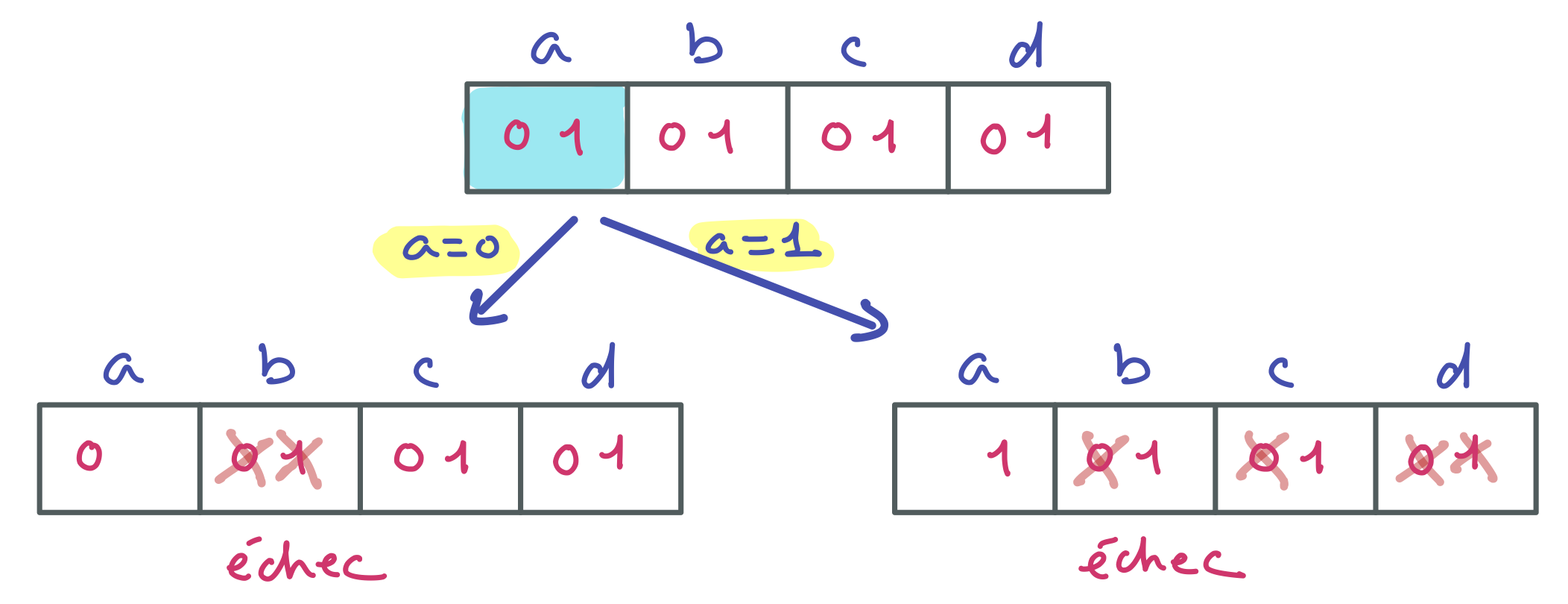
Puisque $a = 1$, $b = 0$ n’a pas de support pour la clause $(\neg a \vee b)$ qui ne peut être satisfaite que si $b = 1$. Cette première étape peut aussi être formalisée comme ci-dessous en termes de propagation unitaire.
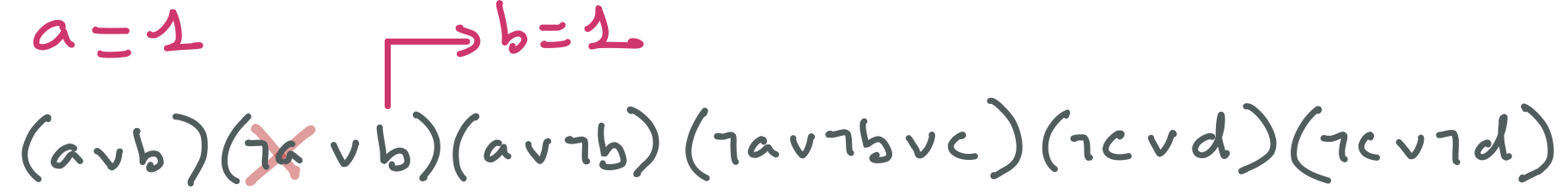
Ensuite, puisque le domaine de $b$ est ${ 1}$, ce qui revient à dire que $b = 1$, et que par ailleurs $a = 1$, $c = 0$ n’a pas de support pour la clause $(\neg a \vee \neg b \vee c)$ qui ne peut être satisfaite que si $c = 1$.
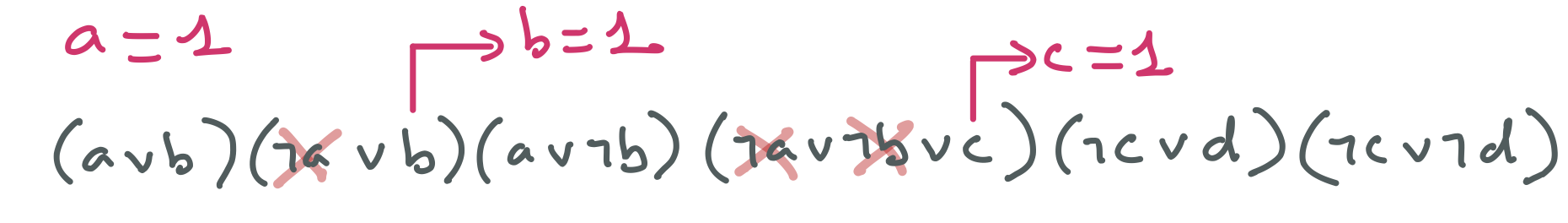
Mais avec $c = 1$, $d = 0$ n’a plus de support pour la clause $(\neg c \vee d)$ et $d = 1$ n’a plus de support pour la clause $(\neg c \vee \neg d)$. Le domaine de $d$ se retrouve vide et la branche aboutit à un échec. Le réseau initial est donc incohérent.