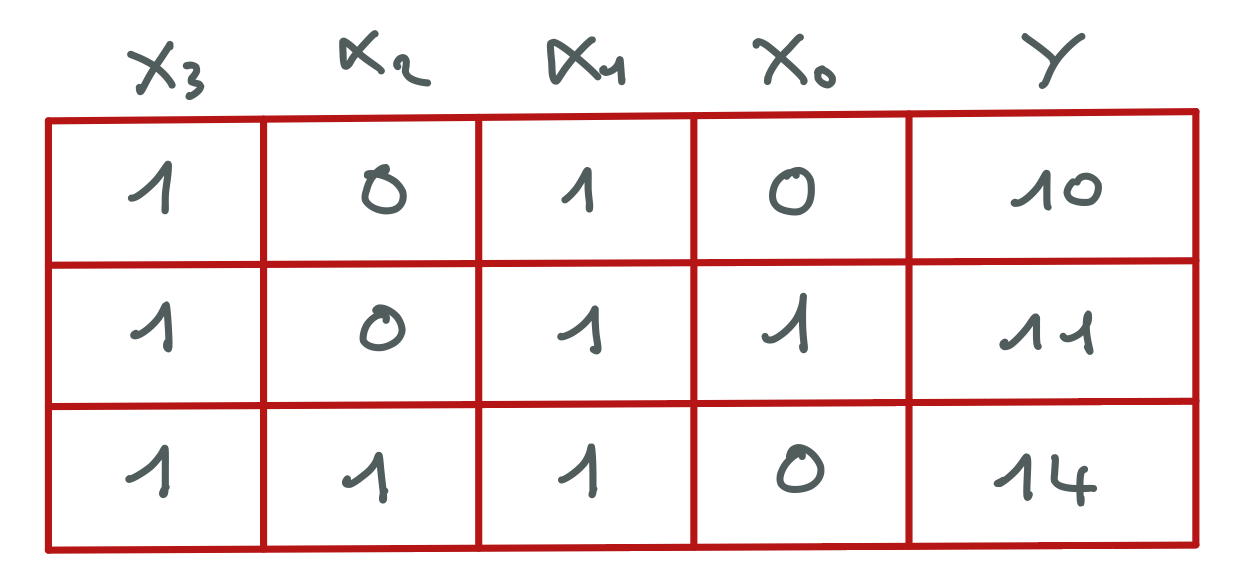
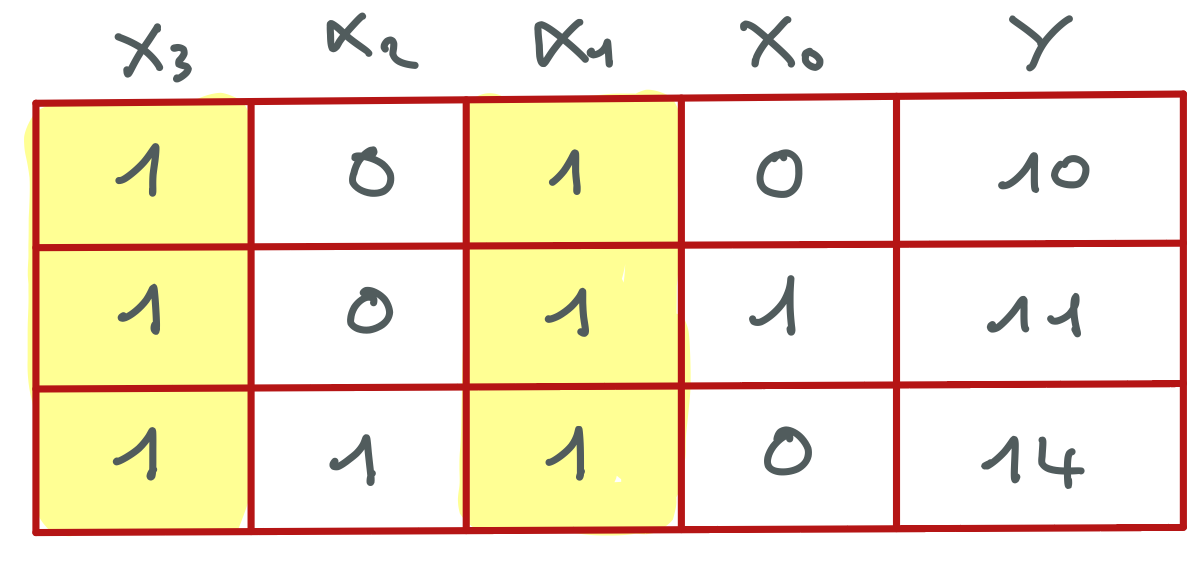
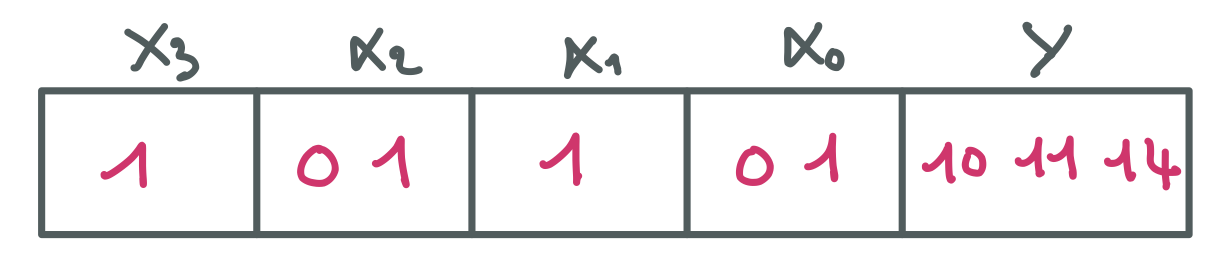
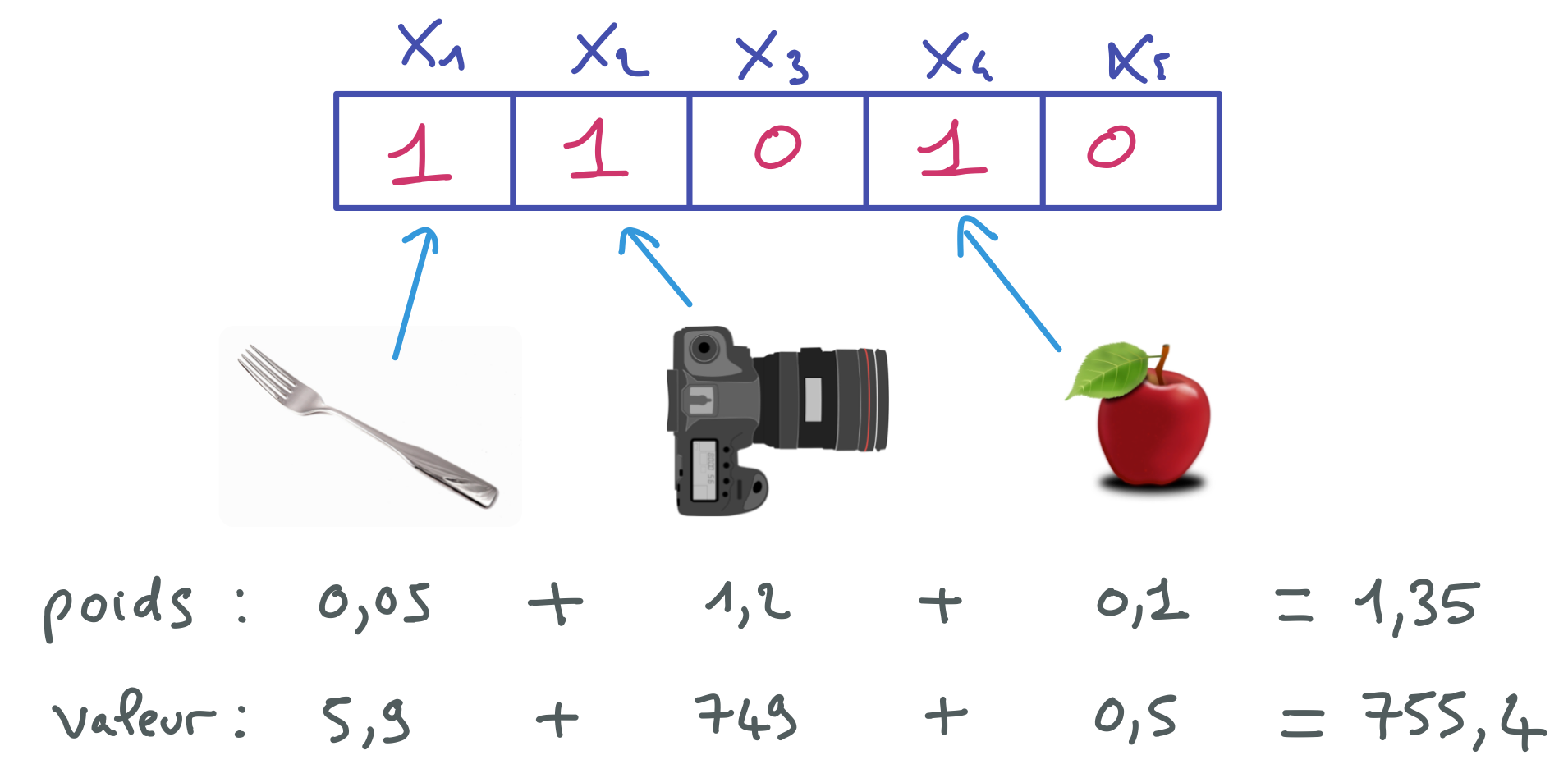
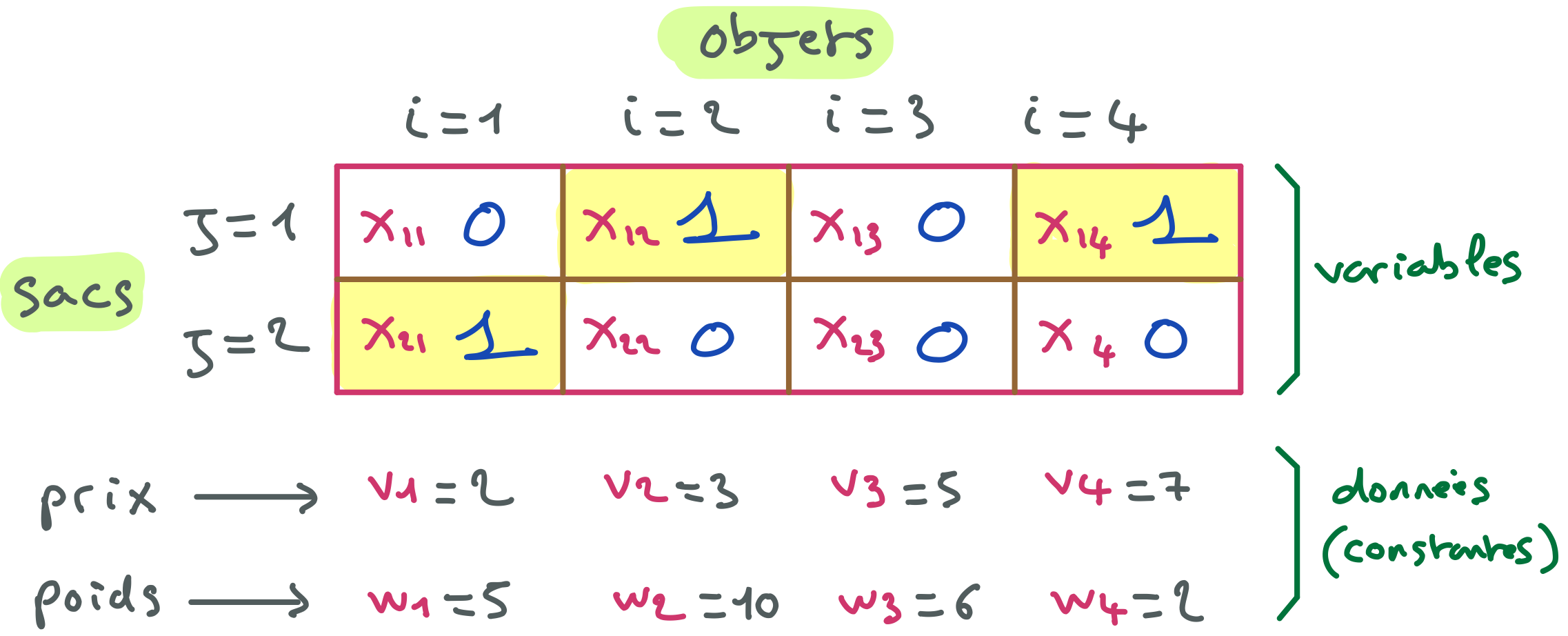
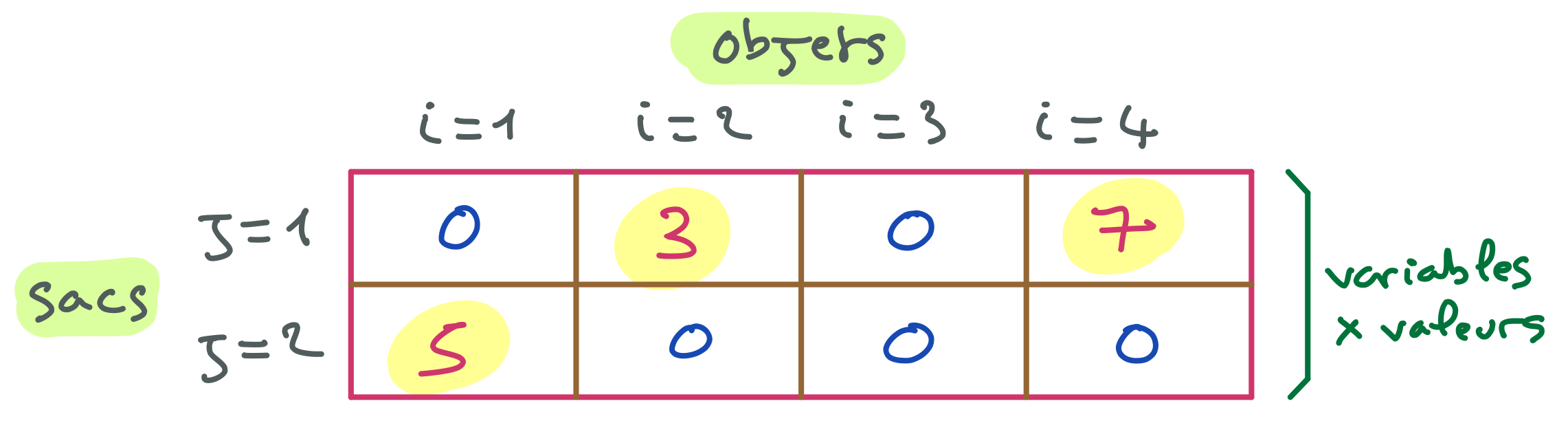
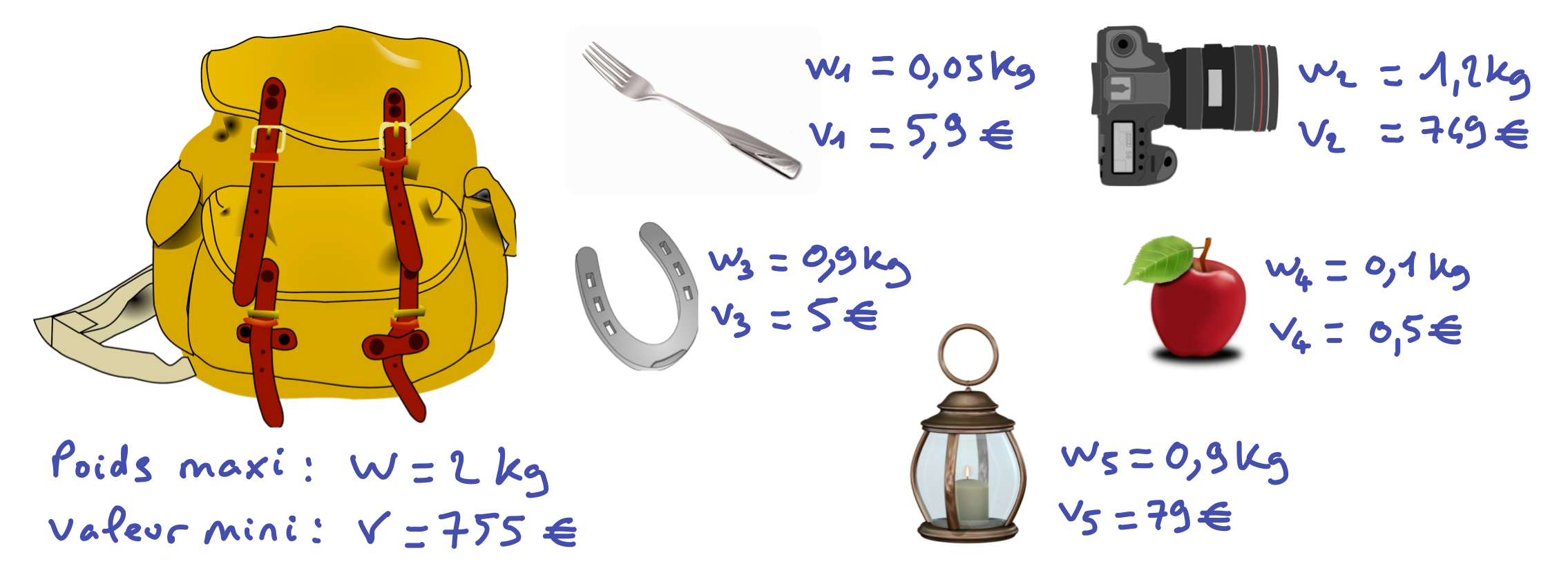Partie B
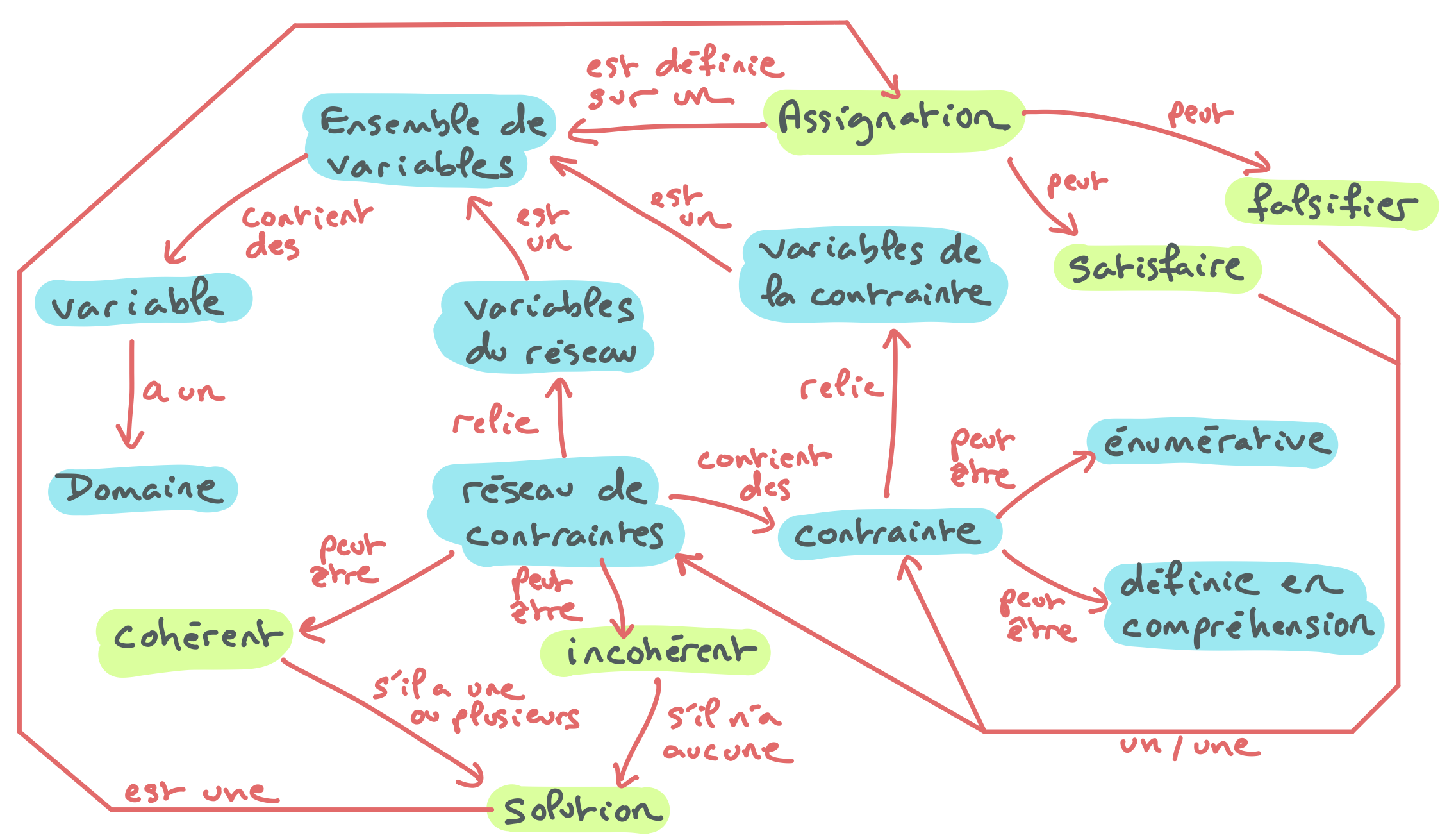
Classes et objets
Objectif
Être capable d’implémenter une classe comportant des attributs (variable d’instance), des méthodes d’instance, des constructeurs, exploitant des données représentées par des types primitifs, des tableaux, des chaînes, des listes de type ArrayList, et des classes enveloppes (telles que Integer, Double…). Être capable d’utiliser une telle classe en maîtrisant les effets de bord induits par les attributs modifiables. Être capable de réaliser une application utilisant plusieurs classes par composition (sans héritage) et de prévoir le comportement d’un tel programme, y compris les objets et données créés dans la mémoire de l’ordinateur (pile, tas, zone des données statiques).
Prérequis
Partie A
B1 : Exemple introductif
Présentation
Nous allons maintenant aborder la « vraie » programmation orientée objet, c’est à dire la création d’instances de classes, donc d’objets, et l’utilisation de méthodes d’instances pour agir sur ces objets.
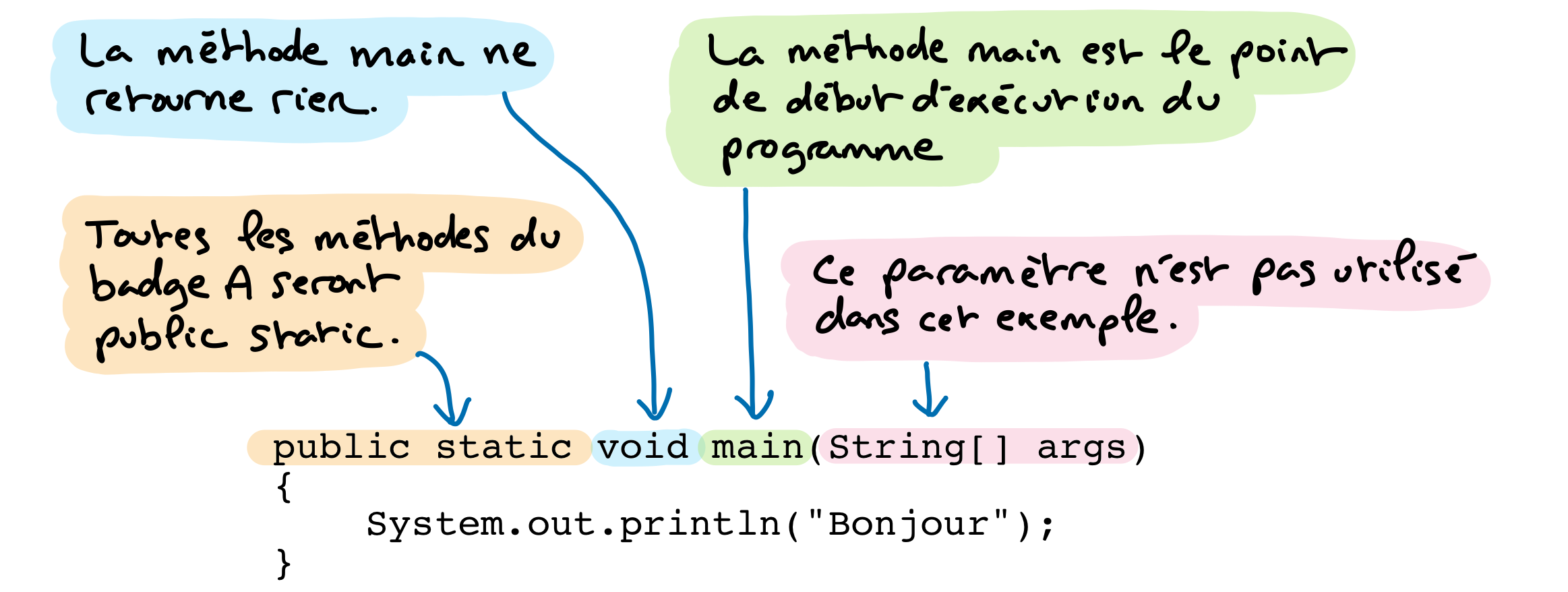
Voici un exemple introductif avec une classe Date qui modélise une date constituée d’un jour, d’un mois et d’une année. Java dispose déjà d’une classe Date, mais on peut utiliser un même nom pour des classes différentes, à condition qu’elles soient dans des packages différents.
public class Date
{
private int jour;
private int mois;
private int annee;
public Date()
{
this.jour=1; this.mois=1; this.annee=1900;
}
public Date(int jour, int mois, int annee)
{
this.jour=jour; this.mois=mois; this.annee=annee;
}
public String toString()
{
return this.jour + "/" + this.mois + "/" + this.annee;
}
}
Détaillons les différents éléments de cette classe. Voici la déclaration de trois attributs aussi appelés variables d’instance.
private int jour;
private int mois;
private int annee;
Ces trois attributs sont privés. Ils ne sont accessibles que depuis les méthodes de la classe Date. Chaque instance de la classe, c’est-à-dire chaque objet créé d’après cette classe, dispose de ses propres exemplaires de ces attributs.
Ensuite nous avons la définition d’un premier constructeur.
public Date()
{
this.jour=1; this.mois=1; this.annee=1900;
}
Un tel constructeur sans paramètre est appelé constructeur pas défaut. Comme tout constructeur, son rôle est d’initialiser une instance de la classe lors de sa construction lancée par l’opérateur new.
Voici maintenant un deuxième constructeur qui accepte 3 paramètres.
public Date(int jour, int mois, int annee)
{
this.jour=jour; this.mois=mois; this.annee=annee;
}
Comme dans le constructeur par défaut, les attributs initialisés sont préfixés par this, qui est la référence de l’objet en cours de construction. Dans le premier constructeur, ce préfixe est facultatif. Mais ici il permet de distinguer les attributs des paramètres de mêmes noms. Si on écrivait…
public Date(int jour, int mois, int annee)
{
jour=jour; mois=mois; annee=annee;
}
… ce constructeur n’aurait strictement aucun effet sur les attributs de la classe, ni sur autre chose d’ailleurs puis qu’il recopierait le contenu du paramètre jour dans lui-même, et pareillement pour mois et annee.
Nous avons ensuite une méthode d’instance.
public String toString()
{
return this.jour + "/" + this.mois + "/" + this.annee;
}
Cette méthode n’a aucun paramètre et retourne une chaîne de caractère qui décrit l’objet courant, c’est-à-dire l’objet via lequel elle est appelée. Ici, le préfixe this est facultatif, mais il a le mérite de bien mettre en évidence les attributs.
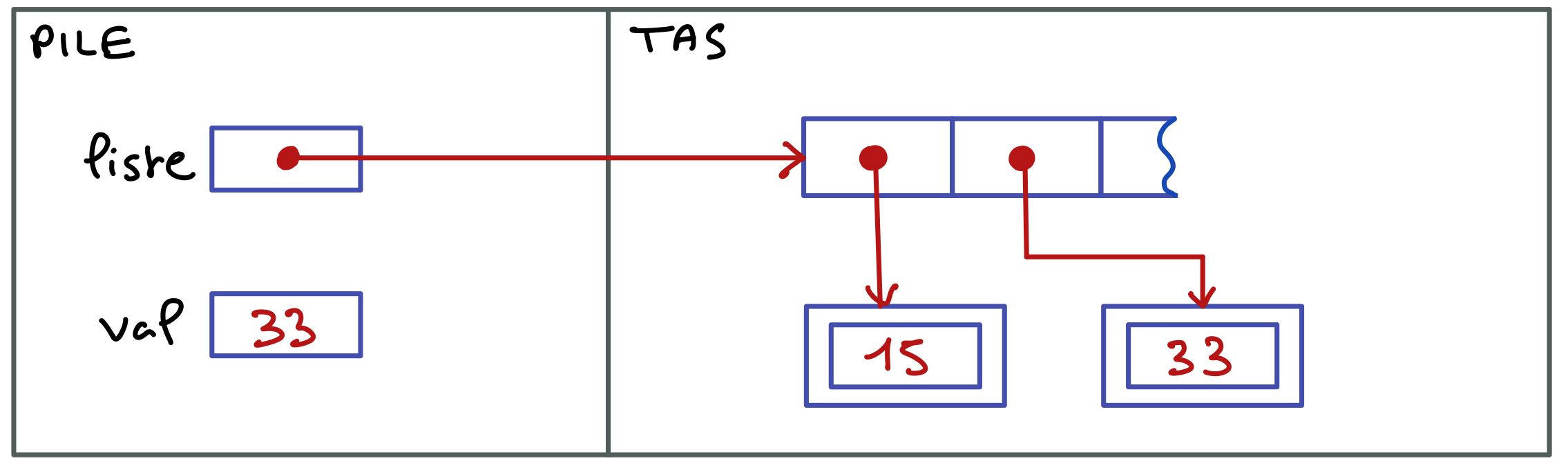
Maintenant que nous avons une classe, nous pouvons l’utiliser pour créer des instances et les utiliser. Voici un exemple simple.
public class Main
{
public static void main(String[] args)
{
Date d1 = new Date(11,9,2017);
Date d2 = new Date();
System.out.println(d1.toString());
System.out.println(d2.toString());
}
}
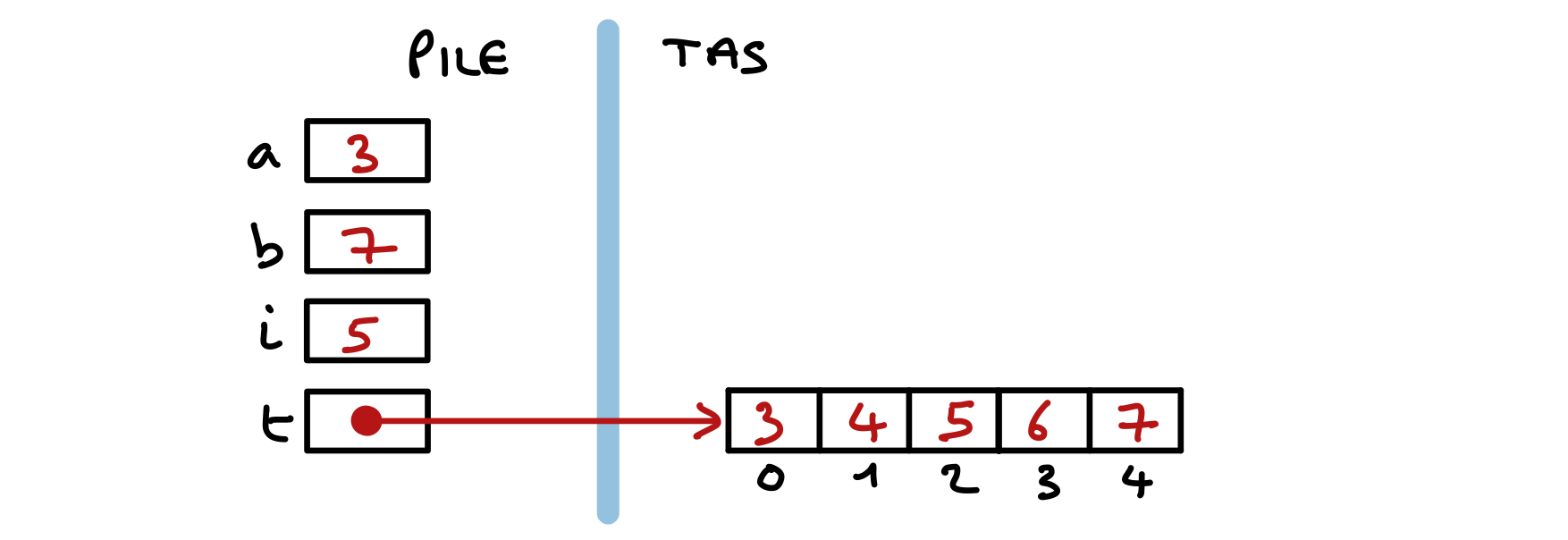
Les deux premières lignes de la méthode main font respectivement appel aux deux constructeurs de la classe Date.
Date d1 = new Date(11,9,2017);
Date d2 = new Date();
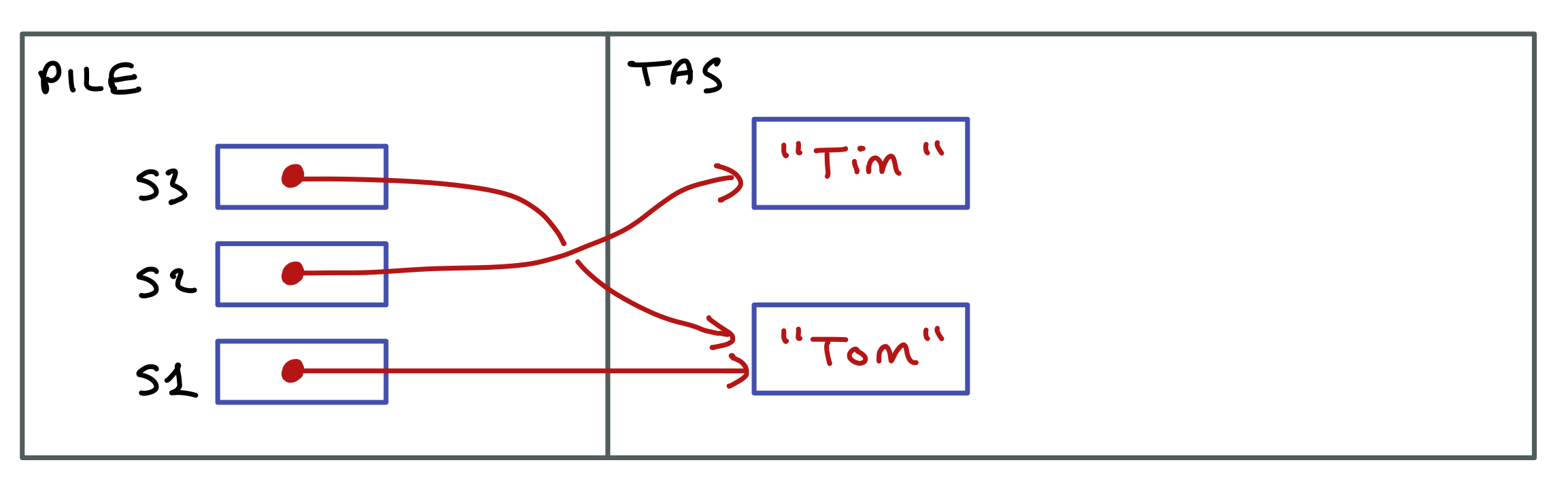
Les références des objets créés sont placées dans deux variables de méthode. Voici ce qui se passe en mémoire.
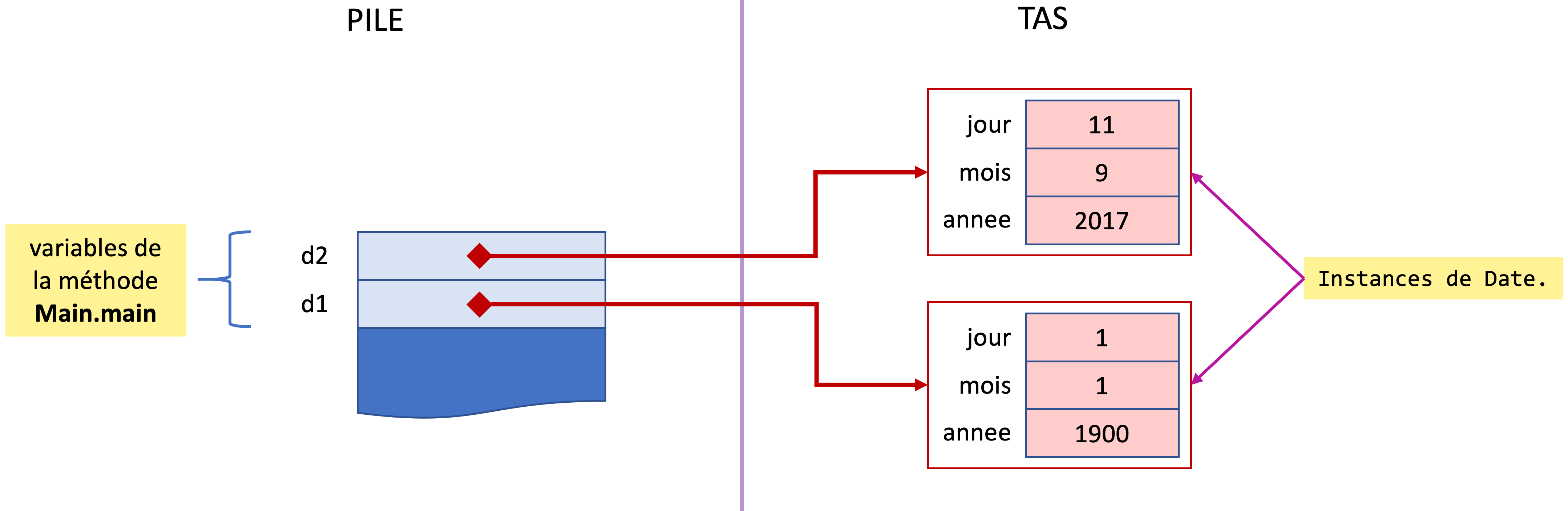
Les deux lignes suivantes appellent la méthode toString avec chacune des deux instances et affiche les chaînes retournées.
System.out.println(d1.toString());
System.out.println(d2.toString());
Le résultat est l’affichage suivant…
1/9/2017
1/1/1900
Quelques précisions
Constructeur par défaut
Lorsqu’on ne définit aucun constructeur dans une classe, Java crée un constructeur par défaut qui initialise chaque variable d’instance avec une valeur par défaut : 0 pour un entier, 0.0 pour un flottant, null pour une référence… Dès lors qu’on définit un constructeur avec paramètre(s), aucun constructeur par défaut n’est produit de manière automatique. Si on en veut un, il faut le définir. Dans notre exemple, le constructeur par défaut ne sert pas à grand-chose d’autre qu’illustrer le concept.
Destruction d’une instance
Toute instance est détruite automatiquement par la machine virtuelle dès lors qu’aucune variable ne contient sa référence. Le programmeur n’a donc pas à se soucier du recyclage de la mémoire.
Éditer et compiler ses programmes
Dans une application qui contient plusieurs classes, les bytecodes de ces classes sont regroupés dans un fichier ayant l’extension «.jar». On peut les produire en ligne de commande, via une console ou avec un script, mais Il existe des logiciels appelés IDE qui facilitent l’édition, la compilation et la mise au point des programmes, comme par exemple : NetBeans, Eclipse, IntelliJ IDEA, BlueJ (à vocation pédagogique !)… Je vous conseille d’en utiliser un.
Exercices de découverte
B-dec-10
Quels éléments syntaxiques (notation) permettent de savoir si une variable est une variable de méthode, une variable d’instance (aussi appelée attribut) ou une variable de classe dans un code Java ?
"Solution"
Les variables de méthodes sont déclarées uniquement à l’intérieur d’une méthode. La déclaration d’une variable de classe comporte le mot clé static. Les variables déclarées à l’extérieur d’une méthode sans le mot clé staticsont des variables d’instance, aussi appelée attributs.
B-dec-11
Quels éléments syntaxiques (notation) permettent de savoir si une méthode est une méthode de classe ou une méthode d’instance ?
"Solution"
La définition d’une méthode de classe comporte le mot clé static, contrairement à celle d’une méthode d’instance.
B-dec-12
On considère la classe Date définie précédemment et la classe Main suivante.
public class Main
{
public static void main(String[] args)
{
Date d = new Date();
d.annee = 1905;
System.out.println(d.toString());
}
}
Il y a une erreur. Trouvez là sans utiliser d’IDE ni de compilateur Java.
"Solution"
L’attribut annee de la classe Date est private. la méthode main est dans une autre classe et ne peut donc pas accéder à cet attribut.
B-dec-13
Ajoutez dans la classe Date un constructeur acceptant un seul paramètre de type int et qui permet de créer une instance de Date représentant le premier janvier de l’année passée en paramètre.
"Solution"
public Date(int annee)
{
this.jour = 1; this.mois = 1; this.annee = annee;
}
B2 : Accesseurs et bonnes pratiques
A l’instar de ce qui est fait dans notre classe Date, le fait de rendre private les variables d’instance est considéré comme une bonne pratique en programmation objet. Plutôt que de permettre aux « utilisateurs » de la classe d’accéder directement à ces variables, on préfère mettre à sa disposition des méthodes publiques appelées accesseurs.
Voici les accesseurs de la classe Date qui ont été produits automatiquement par mon IDE.
int getJour()
{
return jour;
}
public int getAnnee()
{
return annee;
}
public int getMois()
{
return mois;
}
public void setAnnee(int annee)
{
this.annee = annee;
}
public void setMois(int mois)
{
this.mois = mois;
}
public void setJour(int jour)
{
this.jour = jour;
}
Avec cette approche, on pourrait changer la représentation en mémoire d’une date, par exemple en utilisant un seul entier qui combinerait le jour, le mois et l’année avec une formule du genre (d = année x 10000 + mois x 100 + jours) sans avoir à changer quoi que ce soit dans les méthodes utilisant la classe Date. Il suffirait de modifier le code des accesseurs pour que tout fonctionne correctement.
Par exemple getMois() retournerait (d/100)%10000 et setMois(int m) effectuerait l’opération d = getAnnee()*10000 + m*100 + getJour().
Exercices de découverte
B-dec-20
Réalisez une méthode d’accès setDate permettant de modifier simultanément le jour, le mois et l’année de l’instance courante de la classe Date. Cette méthode doit avoir trois paramètre nommés jour, mois et annee.
"Solution"
public void setDate(int jour, int mois, int annee)
{
this.jour = jour; this.mois = mois; this.annee = annee;
}
B-dec-21
Donnez les lignes de code permettant de créer une instance de Date avec le constructeur par défaut de la classe Date, puis de modifier cette instance à l’aide de la méthode setDate de façon à ce que la date représentée soit le 12/10/2005.
"Solution"
Date d = new Date();
d.setDate(12, 10, 2005);
B3 : Composition de classes
On parle de composition de classes lorsqu’une classe a des attributs ayant pour types d’autres classes. Par exemple on peut définir une classe Periode dont les attributs désignent deux instances de Date et une instance de String.
public class Periode
{
private Date debut;
private Date fin;
private String nom;
// À compléter
}
Chacun des deux attributs debut et fin peut contenir une référence d’une instance de Date. Ces instances ont vocation à représenter le début et la fin d’une période constituée d’une ou plusieurs journées. Le troisième attribut est de type String. Il a vocation à contenir la référence d’une instance de String, c’est-à-dire une chaîne de caractères qui donne un nom à la période représentée.
On peut ajouter dans notre classe le constructeur suivant…
public Periode(Date deb, Date fin, String nom)
{
this.debut = deb;
this.fin = fin;
this.nom = nom;
}
…puis la méthode toString suivante…
public String toString()
{
return "[ " + nom + " " + debut + " - " + fin + " ]";
}
…et une méthode permettant de tester la classe…
public static void test()
{
Date d1 = new Date(4, 9, 2018);
Date d2 = new Date(19, 9, 2018);
Periode p = new Periode(d1, d2, "Vacances");
System.out.println(p.toString());
}
Notez bien que test est une méthode de classe qui ne nécessite pas d’objet de type Periode pour être appelée, et qui créée elle-même un objet de ce type. Pour appeler cette méthode test, par exemple depuis une méthode main, on écrit simplement…
Periode.test();
L’affichage obtenu est…
[ Vacances 4/9/2018 - 19/9/2018 ]
Voici ce qui se passe dans la mémoire…
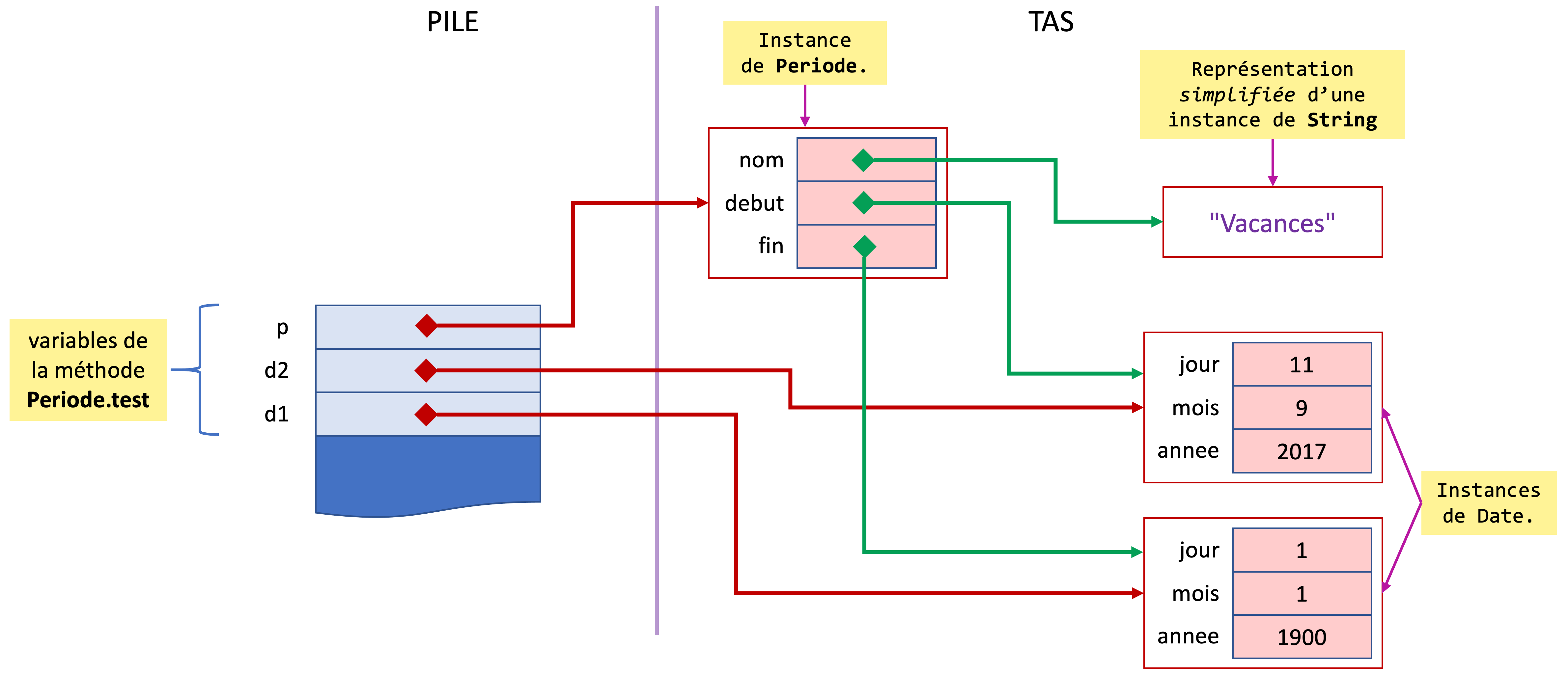
Exercices de découverte
B-dec-30
On considère deux variantes d’un constructeur de la classe Periode. En pratique, il faudra en choisir une car on ne peut implémenter dans une même classe deux constructeurs ayant exactement les mêmes paramètres.
/// Version 1
public Periode(Periode m)
{
this.debut = m.debut;
this.fin = m.fin;
this.nom = m.nom;
}
/// Version 2
public Periode(Periode m)
{
this.debut = new Date(m.debut.getJour(), m.debut.getMois(), m.debut.getAnnee());
this.fin = new Date(m.fin.getJour(), m.fin.getMois(), m.fin.getAnnee());
this.nom = m.nom;
}
On considère les lignes de code suivantes.
Date d1 = new Date(4, 9, 2018);
Date d2 = new Date(19, 9, 2018);
Periode p = new Periode(d1, d2, "Vacances");
Periode q = new Periode(p);
d1.setJour(5);
System.out.println(p.toString());
System.out.println(q.toString());
Donnez les affichages obtenus dans le cas où la version 1 du constructeur à 1 paramètre est utilisée et dans le cas où la version 2 est utilisée.
"Solution"
Version 1 :
[Vacances 5/9/2018 - 19/9/2018]
[Vacances 5/9/2018 - 19/9/2018]
Version 2 :
[Vacances 5/9/2018 - 19/9/2018]
[Vacances 4/9/2018 - 19/9/2018]
Pour bien comprendre ce résultat, il faut dessiner la configuration en mémoire dans les deux scénarios. Avec la version 1 du constructeur, il n’y a au total que deux objets de type Date dans le tas. Avec la version 2, on a deux new Date(...) en plus et au total 4 objets de type Datedans le tas. Dans le premier cas, les attributs debut des instances de Periode désignées par p et q pointent sur une même instance de Date. Si on la modifie, cela se répercute sur les deux périodes. Dans le deuxième cas, les attributs debut des instances de Periode désignées par p et q pointent sur deux instances de Date distinctes. Modifier l’une d’elle n’a pas d’effet sur l’autre.
B4 : Composition par tableaux
Dans cet exemple, nous créons une classe Memo qui contient plusieurs dates stockées dans un tableau. Cette classe a surtout une vocation pédagogique : montrer comment gérer un tableau référencé par une variable d’instance et comment les instances de la classe concernée sont représentées en mémoire.
public class Memo
{
private Date[] tab;
private int nDates;
// À compléter
}
Une instance de cette classe représente une liste de dates, chacune représentée par une instance de Date. Un tableau est utilisé à cette fin, dans un but plus pédagogique que pratique. Examinons d’abord le constructeur de la classe…
public Memo(int n)
{
tab = new Date[n]; nDates=0;
}
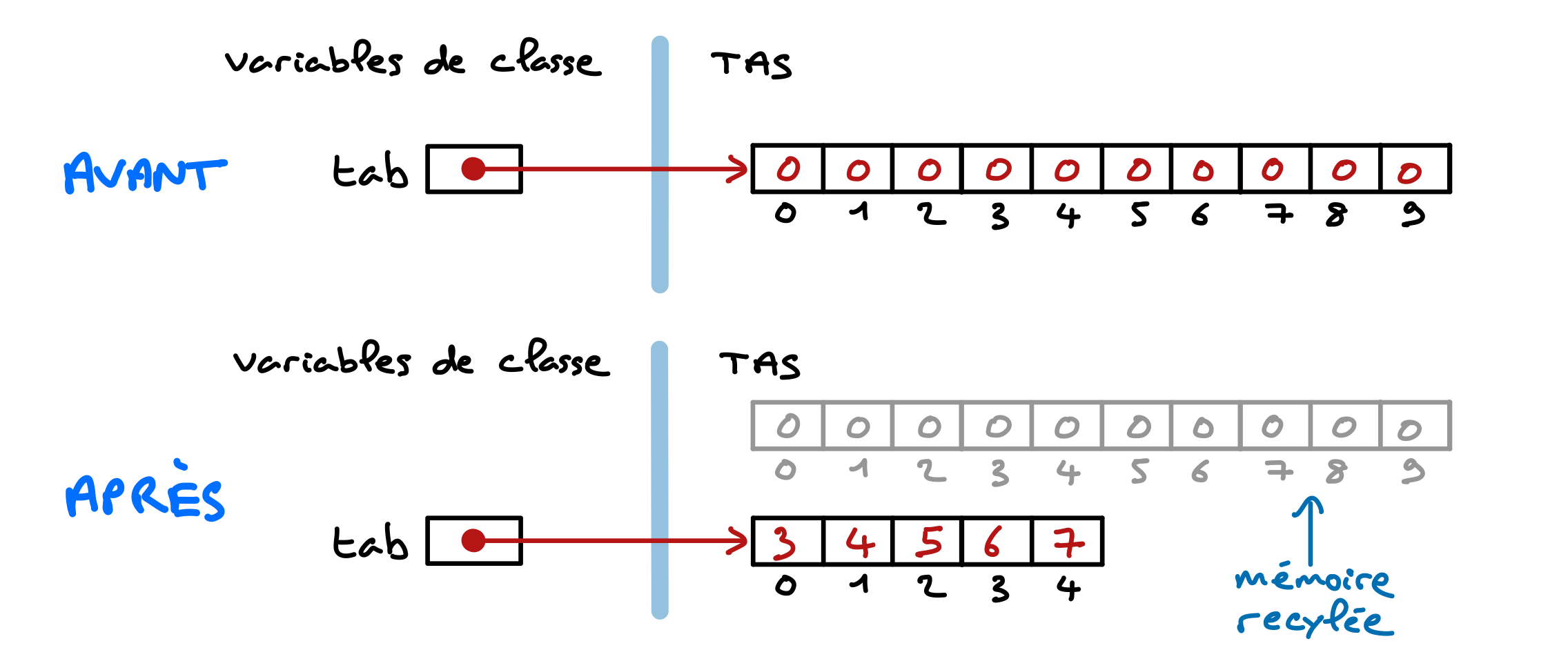
Ce constructeur accepte en paramètre la capacité du mémo, c’est-à-dire le nombre maximum de dates qu’il va pouvoir contenir. Cela correspond à la taille du tableau désigné par l’attribut tab. L’attribut nDate indique le nombre de dates effectivement stockées dans le mémo. Cet attribut est donc initialisé à 0, puisqu’à sa création le mémo est vide. Incidemment, chaque cellule du tableau créé contient la référence null.
Pour ajouter une date à une instance de Memo, on adjoint à la classe une méthode add définie de la manière suivante…
public void add(Date d)
{
if(nDates >= tab.length)
{
System.out.println("Tableau plein !");
}
else
{
tab[nDates] = d; nDates++;
}
}
On passe en argument à add la référence d’une instance de Date à ajouter au mémo. Mais comme le tableau de stockage a une taille limitée, déterminée à sa création, on vérifie qu’il reste encore de la place en comparant le nombre de dates enregistrées avec la longueur (tab.length) du tableau de stockage.
Dans le cas où il reste de la place, la référence de l’instance de Date à ajouter est placée dans la première cellule libre du tableau, qui a pour indice la valeur de l’attribut nDate. Cette valeur est ensuite augmentée de 1 pour refléter le nouveau nombre de dates stockées dans le mémo.
Ajoutons à notre classe Memo une méthode d’affichage…
public void print()
{
for(int i=0; i<nDates; i++)
{
System.out.println(tab[i].toString());
}
}
Puis testons ce que nous avons programmé avec la méthode suivante, qui peut se trouver dans la classe Memo ou ailleurs.
public static void test()
{
Memo m = new Memo(5);
m.add(new Date(12,10,2017));
m.add(new Date(14,12,2017));
m.print();
}
Voici la situation en mémoire à la fin de l’exécution de cette méthode.
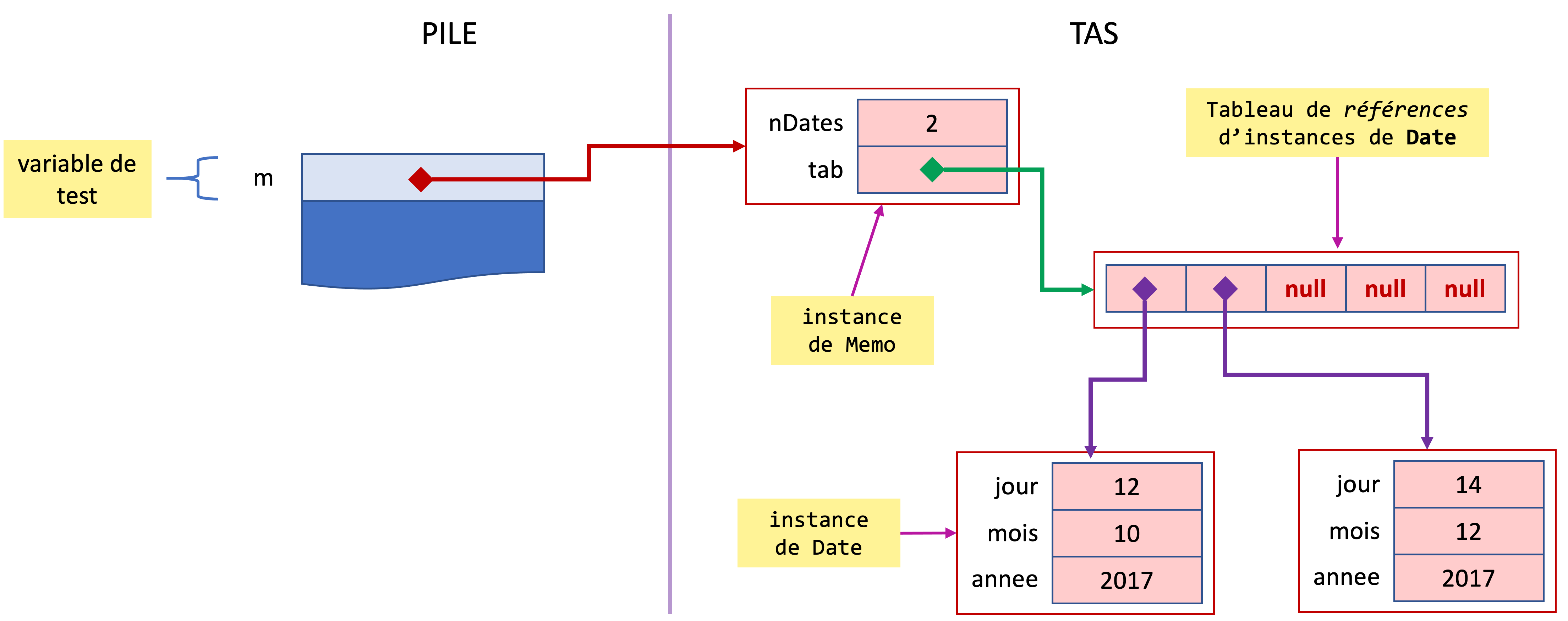
Exercices de découverte
B-dec-40
Réalisez une méthode d’instance read de la classe Memo permettant de récupérer la référence de la date située à une position donnée en argument dans l’instance courante de Memo. Si m désigne une instance de Memoet i est un entier positif ou nul alors l’appel m.read(i) doit retourner…
- la référence de la date située en position
i dans le mémo s’il contient au moins i+1 dates,
- la valeur
null dans le cas contraire.
Les positions sont numérotées à partir de 0 comme il est d’usage en programmation.
"Solution"
public Date read(int i)
{
if(i >= nDates) return null;
else return this.tab[i];
}
B-dec-41
Réalisez un constructeur de la classe Memo permettant de créer un mémo contenant exactement deux dates.
public Memo(Date d1, Date d2)
{
// À compléter
}
"Solution"
public Memo(Date d1, Date d2)
{
tab = new Date[2]; nDates=2;
tab[0] = d1;
tab[1] = d2;
}
B5 : La classe standard ArrayList
Comme nous l’avons vu dans l’exemple de la classe memo, l’utilisation d’un tableau comporte une limitation assez embêtante : sa taille doit être fixée une fois pour toute lors de sa création. Pour éviter ce problème, on peut utiliser une classe nommée ArrayList permettant de faire des listes extensibles.
Cette classe est générique, dans le sens où elle peut être paramétrée par un type. ArrayList<T> représente une liste de références d’instances de T. Une telle liste est plus souple d’utilisation qu’un tableau car sa capacité n’est pas limitée (du moins elle n’est limitée que par les ressources mémoire allouées à la machine virtuelle java).
Exemple introductif
Examinons un exemple. Je veux créer une liste de dates (techniquement, d’instances de la classe Date). J’écris simplement…
ArrayList<Date> t = new ArrayList<>();
Une liste vide est créée dans le tas et sa référence est placée dans w. Cette liste à une capacité initiale de 10 emplacements (valeur par défaut allouée par le compilateur), mais cette capacité sera automatiquement augmentée si on y place plus de 10 éléments.
J’ajoute deux dates à ma liste…
t.add(new Date(1,1,1901));
t.add(new Date(2,2,1902));
Examinons ce qui s’est passé dans la mémoire.
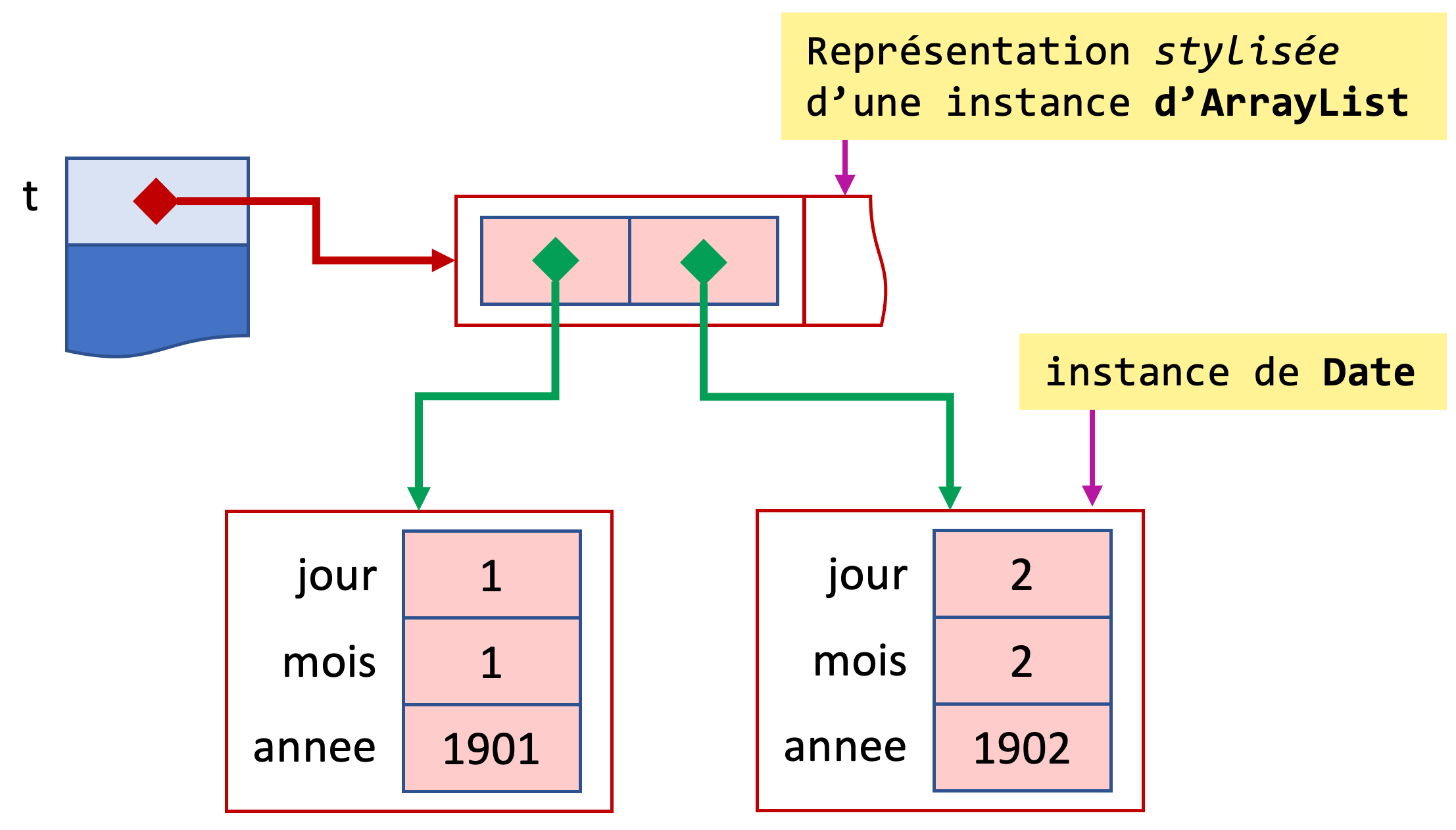
La représentation d’une instance d’ArrayList a été simplifiée (tout comme celle des instances de String que nous avons eu l’occasion de voir précédemment). En réalité, une instance d’ArrayList comporte plusieurs attributs dont un désigne un tableau qui pourra être remplacé par un autre de taille différente à chaque fois que c’est nécessaire. Mais puisque cette classe a été créée pour nous simplifier la vie, autant en simplifier la représentation.
Précisions sur la classe ArrayList<T>
L’essentiel à savoir concernant la classe ArrayList<T>, c’est que :
- toute instance
w contient w.size() éléments,
- tout élément est soit une référence de type
T, soit null.
- la position de chaque élément est désignée par un indice,
- le premier élément a pour indice 0.
Voici quelques méthodes de la classe ArrayList. Il y en a beaucoup d’autres, que vous pourrez trouver dans la documentation officielle à l’URL https://docs.oracle.com/javase/8/docs/api/
int size() : retourne le nombre d’éléments stockés.boolean add(T e) : ajoute l’élément e en fin de liste. La valeur de retour est toujours true. Elle peut être ignorée.void add(int i, T e) : ajoute l’élément e en position i et décale (si applicable) les éléments suivants d’une position. La plus grande valeur autorisée pour i est size().T get(int i) : retourne l’élément situé en position i. La plus grande valeur autorisée pour i est size()-1.T remove(int i) : retire l’élément situé en position i et le retourne. Les éléments suivants (si applicable) sont décalés d’une position pour boucher le « trou ».int indexOf(Object e) : retourne l’indice de la position de la première occurrence de l’objet e dans la liste, ou -1 si cet objet n’est pas dans la liste. (Toute référence a le type Object par héritage.)T set(int i, T e) : remplace l’élément situé en position i par e.void clear(int i) : retire tous les éléments de la liste.
Un exemple d’utilisation
Soit une classe Personne qui représente une personne et dispose d’une méthode toString permettant d’afficher le nom et le prénom de la personne représentée.
public class Personne
{
private String nom;
private String prenom;
public Personne(String nom, String prenom)
{
this.nom = nom; this.prenom = prenom;
}
publis String toString()
{
return nom + " " + prenom;
}
}
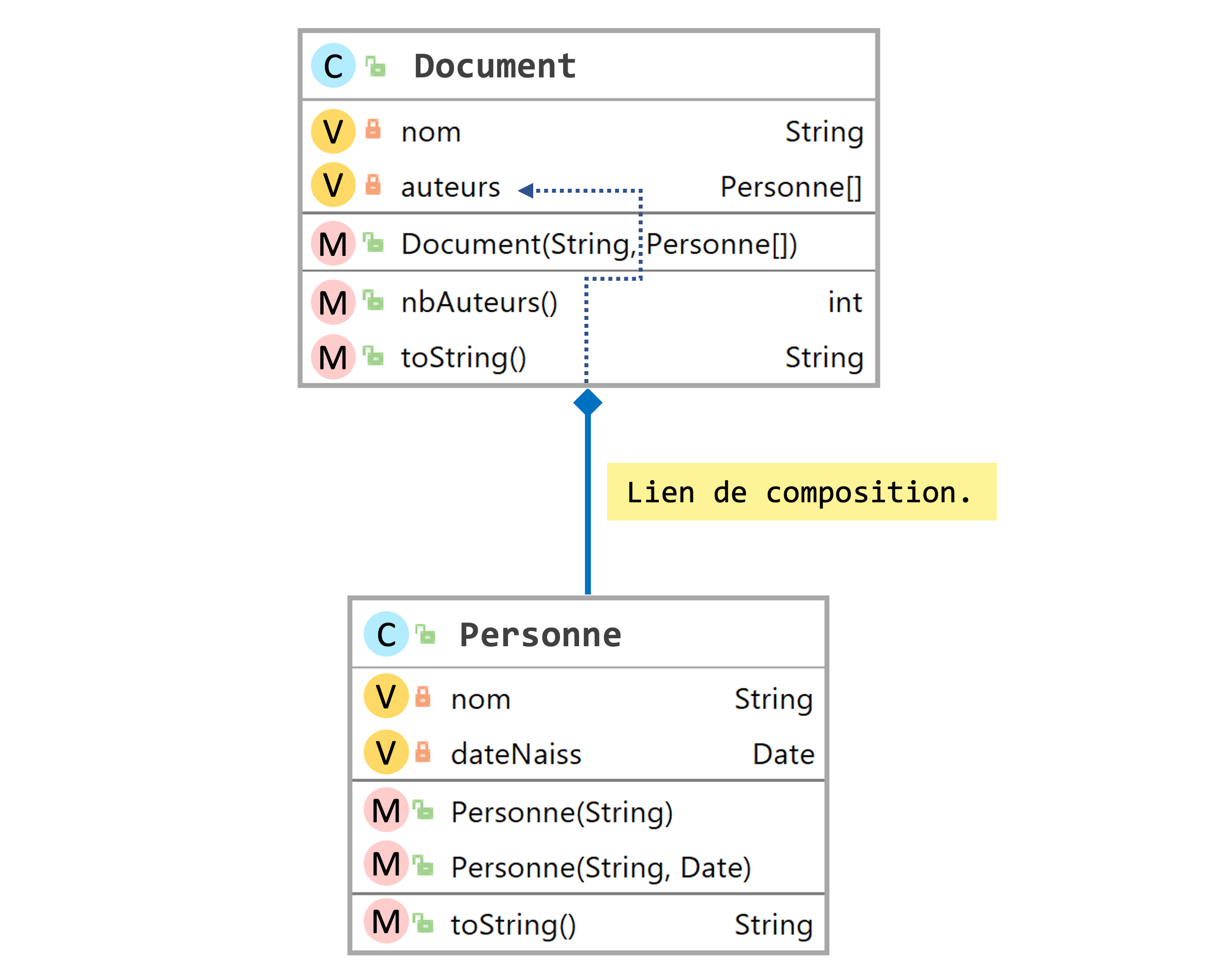
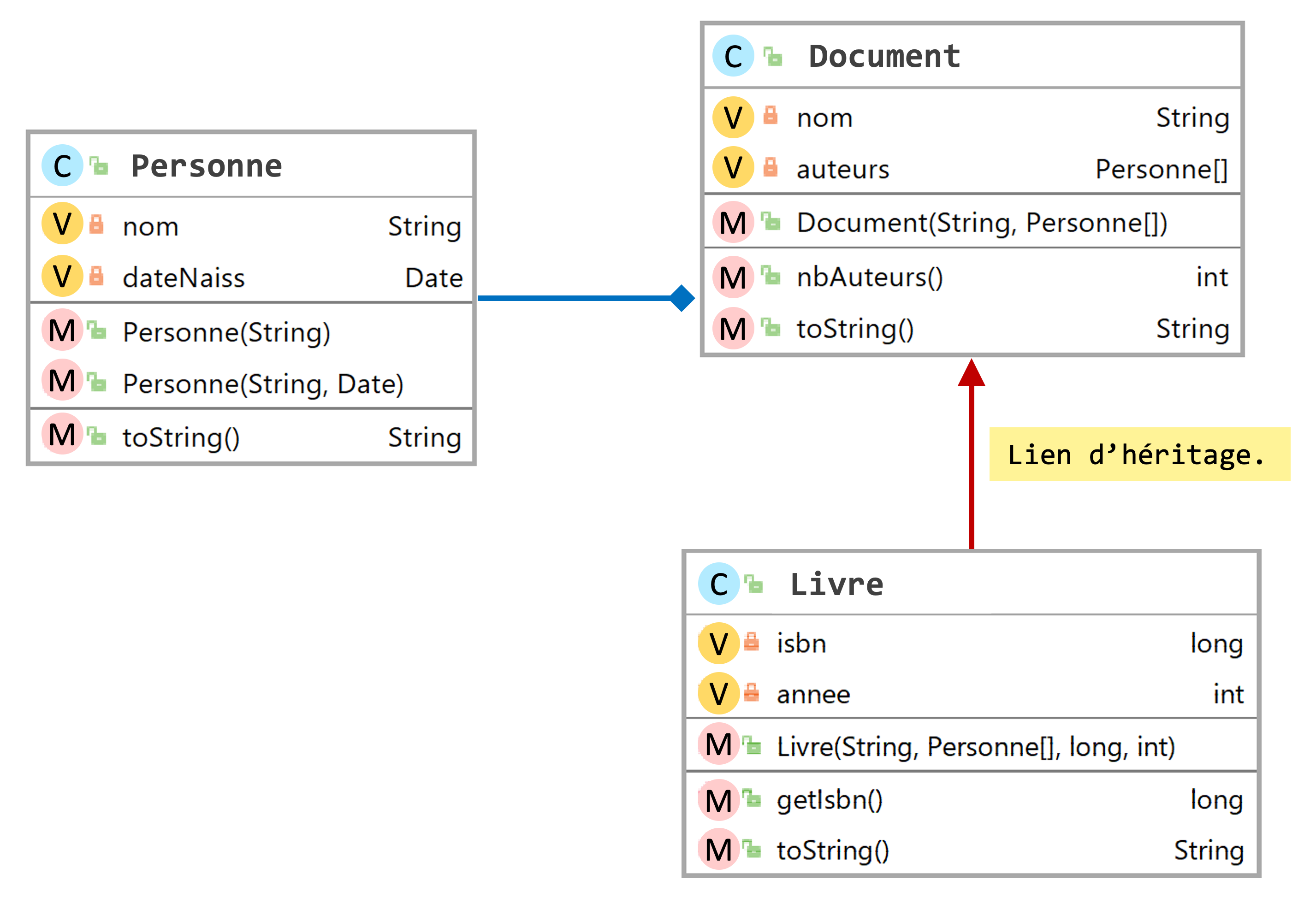
Voici une classe Document dont chaque instance représente un document ayant un nom et des auteurs. Voici les attributs de la classe Document.
public class Document
{
private String nom;
private ArrayList<Personne> auteurs;
// À compléter
}
Pour initialiser ces attributs, il nous faut un constructeur. En voici un…
public Document(String n, Personne[] a)
{
this.nom=n;
auteurs = new ArrayList<Personne>();
for(int i=0; i<a.length; i++)
{
auteurs.add(a[i]);
}
}
Il permet de créer un document en une seule fois, à partir des données reçues en argument, à savoir la référence n d’une chaîne de caractères et un tableau a de références d’instances de la classe Personne. Cela suppose qu’au moment d’utiliser ce constructeur, on dispose de ces données qui ont été préalablement créées.
La première ligne…
this.nom=n;
…place juste dans l’attribut nom la référence d’instance de String contenue dans n.
La ligne suivante…
auteurs = new ArrayList<Personne>();
… appelle le constructeur par défaut de ArrayList<Personne> pour créer une liste vide à laquelle on pourra ajouter autant des références à des instances de Personne que désiré. L’opérateur new retourne la référence de la liste créée, qui est placée dans l’attribut auteurs.
Ensuite, une boucle for…
for(int i=0; i<a.length; i++)
{
auteurs.add(a[i]);
}
… parcourt le tableau passé en argument et ajoute chacune des références qu’il contient à la liste des auteurs du document en cours de construction.
Nous allons ajouter une méthode permettant de récupérer le nombre d’auteurs d’un document…
public int nbAuteurs()
{
return auteurs.size();
}
… qui fait bêtement appel à une méthode de la classe ArrayList retournant le nombre d’éléments de l’instance d’ArrayList concernée.
La méthode suivante, toString, permet de créer une chaîne de caractères donnant une description de l’instance courante de Document.
public String toString()
{
String da = "";
for (int i = 0; i < nbAuteurs(); i++)
{
da = da + auteurs.get(i) + " ";
}
return nom + "\nAuteur(s) : " + da;
}
Notez au passage le moyen utilisé pour récupérer les informations sur les auteurs mérite quelques explications. La ligne…
da = da + auteurs.get(i) + " ";
…récupère la référence désignant l’élément situé en position i dans la liste. Jusque-là rien d’étonnant. Mais ensuite cet élément, qui est de type Personne (entendez par là qu’il s’agit d’une référence d’une instance de Personne), est ajouté à la chaîne en cours de construction grâce à l’opérateur +. Mais attendez, une instance de Personne n’est pas une chaîne de caractère ! Comment Java fait-il pour ajouter une instance de Personne à une chaine de caractères ?
En réalité, dans un tel contexte java remplace implicitement auteurs.get(i) par auteurs.get(i).toString(). C’est une sorte de notation raccourcie qui permet d’ajouter un objet à une chaîne, et qui fonctionne bien si l’objet en question dispose d’une méthode toString correctement programmée. Dans le cas contraire, c’est une chaîne représentant la référence de l’objet concerné qui est ajoutée à la chaîne.
Bon, notre classe Document n’offre pas encore beaucoup de possibilités, mais elle permet de créer et d’afficher des objets de type Document, à condition toutefois de programmer une classe Personne disposant à minima d’un constructeur et d’une méthode toString. Une personne pourrait par exemple être décrite par deux attributs de type String représentant son nom et son prénom.
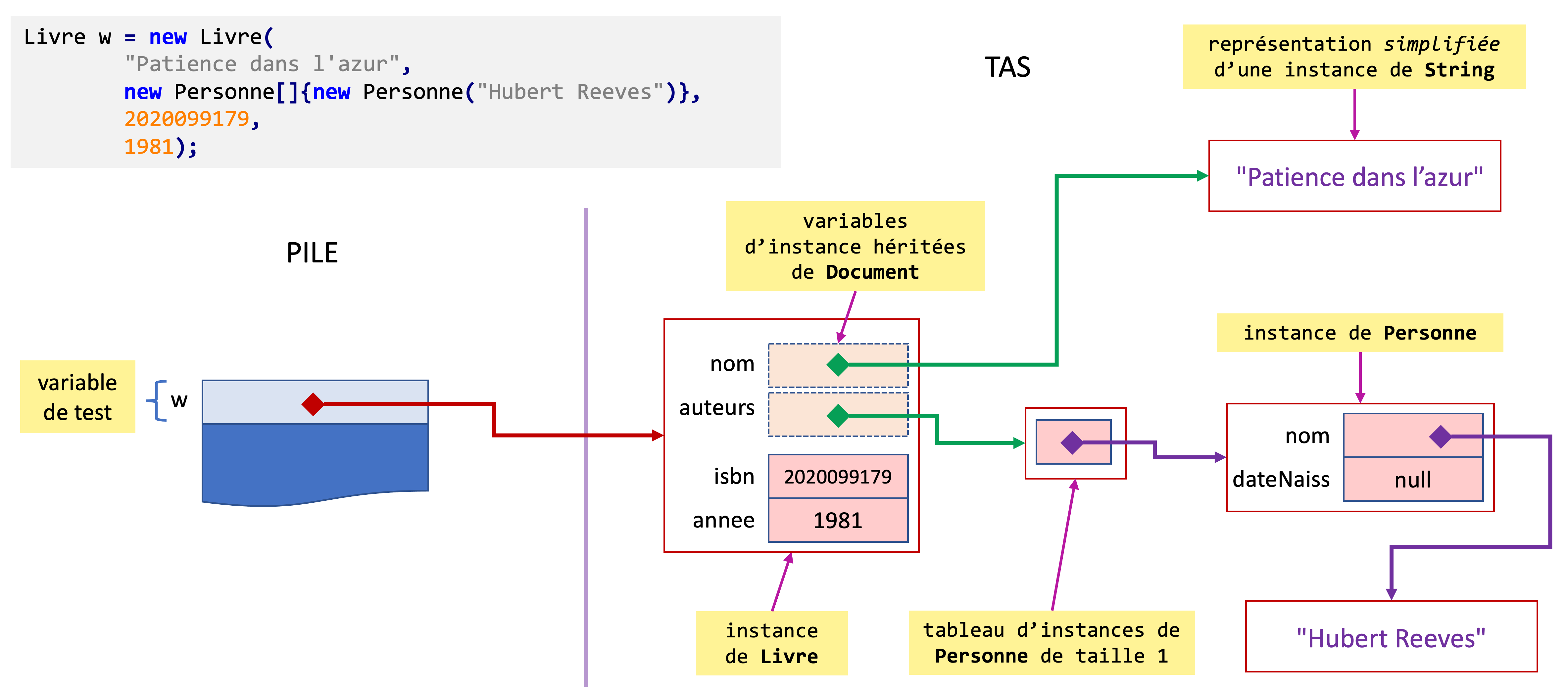
La création d’une instance de Document peut alors prendre la forme suivante…
Personne auteur1 = new Personne("Brian","Kernighan");
Personne auteur2 = new Personne("Dennis","Ritchie");
Document doc = new Document("Le langage C",new Personne[]{auteur1, auteur2});
La syntaxe…
Personne[]{auteur1, auteur2}
…permet de créer un tableau d’instances de Personne et de l’initialiser en même temps.
Exercices de découverte
B-dec-50
Ajoutez à la classe Document un constructeur qui crée une instance représentant un document sans auteur (la liste d’auteurs est vide), mais ayant un nom.
public Document(String nom)
{
// À compléter
}
"Solution"
public Document(String nom)
{
this.nom = nom;
this.auteurs = new ArrayList<Personne>();
}
B-dec-51
Ajoutez à la classe Document une méthode addAuteur permettant d’ajouter un auteur au document courant.
public void addAuteur(Personne p)
{
// À compléter
}
"Solution"
public void addAuteur(Personne p)
{
this.auteurs.add(p);
}
B-dec-52
Ajoutez à la classe Document une autre méthode addAuteur permettant d’ajouter un auteur au document courant.
public void addAuteur(String nom, String Prenom)
{
// À compléter
}
"Solution"
public void addAuteur(String nom, String Prenom)
{
this.auteurs.add(new Personne(nom, prenom));
}
Exercices d’assimilation
B-ass-00
Réalisez une classe Compteur qui comporte un attribut (variable d’instance) cpt de type int, un constructeur par défaut qui initialise cette variable à 0, une méthode d’instance plusUn qui incrémente cette variable, et une méthode d’instance lecture qui retourne la valeur de la variable cpt.
Réalisez une méthode main située dans une classe Main qui crée une instance de Compteur, réalise trois incrémentations de cette instance et affiche sa valeur (i.e., la valeur de sa variable cpt).
"Indice"
public class Compteur
{
private int cpt;
public Compteur()
{
// À compléter
}
public void pluUn()
{
// À compléter
}
public int lecture()
{
// À compléter
}
public static void main(String[] args)
{
Compteur c = new Compteur();
// À compléter
}
}
"Solution"
public class Compteur
{
private int cpt;
public Compteur()
{
cpt = 0;
}
public void pluUn()
{
cpt = cpt + 1;
}
public int lecture()
{
return cpt;
}
public static void main(String[] args)
{
Compteur c = new Compteur();
c.pluUn(); c.pluUn();; c.pluUn();
System.out.println(c.lecture());
}
}
B-ass-01
Réécrivez à la classe Memo (en vous limitant aux attributs, au constructeur à un paramètre et aux méthodes add et print) en remplaçant le tableau par un ArrayList.
"Indice"
public class MemoExt
{
private ArrayList<Date> tab;
public MemoExt()
{
tab = new // À compléter
}
public void add(Date d)
{
// À compléter
}
public void print()
{
for(int i=0; i<tab.size(); i++)
{
// À compléter
}
}
}
L’attribut nDate n’est plus nécessaire car le nombre de dates stockées peut être obtenu avec la méthode size de la classe ArrayList.
"Solution"
public class MemoExt
{
private ArrayList<Date> tab;
public MemoExt()
{
tab = new ArrayList<>();
}
public void add(Date d)
{
tab.add(d);
}
public void print()
{
for(int i=0; i<tab.size(); i++)
{
System.out.println(tab.get(i).toString());
}
}
}
B-ass-02
Réalisez une classe Point qui représente les coordonnées (x,y) d’un point dans un repère cartésien à 2 dimensions. Les coordonnées x et y sont représentées par des nombres en virgule flottantes de type double. La classe Point dispose d’un constructeur permettant de créer un point à partir de ses coordonnées, ainsi que d’une méthode toString, et deux accesseurs getX et getY permettant de récupérer les coordonnées. Elle possède aussi une méthode d’instance public double dist(Point p) qui calcule et retourne la distance entre le point courant et le point désigné par le paramètre p.
La méthode de classe prédéfinie double Math.sqrt(double x), qui retourne la racine carrée de x, vous sera utile.
"Indice"
public class Point
{
private double x;
private double y;
public Point(double x, double y)
{
// À compléter
}
public double getX() {return x;}
public double getY() {return y;}
public String toString()
{
// À compléter
}
public double dist(Point p)
{
double dx = // À compléter
double dy = // À compléter
return Math.sqrt(dx*dx + dy*dy);
}
}
"Solution"
public class Point
{
private double x; private double y;
public Point(double x, double y)
{
this.x = x; this.y = y;
}
public double getX() {return x;}
public double getY() {return y;}
public String toString()
{
return "(" + x + "," + y + ")";
}
public double dist(Point p)
{
double dx = this.x - p.x;
double dy = this.y - p.y;
return Math.sqrt(dx*dx + dy*dy);
}
}
B-ass-03
Réalisez une classe Polygone qui représente un polygone sous la forme d’une liste de points. Cette classe dispose d’un constructeur à trois paramètres de type Point qui produit un triangle et un autre à 4 paramètres de type Point qui produit un quadrilatère. Elle dispose également d’une méthode d’instance perimetre qui retourne la somme des longueurs des côtés du polygone courant et d’une méthode toString qui produit une chaîne indiquant juste le nombre de cotés et le périmètre du polygone courant.
"Indice
public class Polygone
{
private ArrayList<Point> liste;
public Polygone()
{
// À compléter
}
public Polygone(Point a, Point b, Point c)
{
this(); // appelle le constructeur par défaut
// À compléter
}
public Polygone(Point a, Point b, Point c, Point d)
{
this(a, b, c); // appelle le contsructeur de triangle
// À compléter
}
public double perimetre()
{
// À compléter
}
public String toString()
{
// À compléter
}
}
Bien que ce ne soit pas obligatoire, dans cette solution partielle, certains constructeurs utilisent this(...) pour appeler un autre constructeur de manière à éviter de refaire ce que cet autre constructeur sait déjà faire. Ceci évite de répliquer du code identique dans plusieurs constructeurs. Lorsqu’un constructeur en appelle un autre, il faut que cet appel soit réalisé par sa première ligne de code.
"Indice
Voici le code complet des constructeurs et quelques élément de la méthode perimetre. Il vous reste à terminer cette méthode et écrire ma méthode toString.
public Polygone()
{
liste = new ArrayList<>();
}
public Polygone(Point a, Point b, Point c)
{
this();
liste.add(a); liste.add(b); liste.add(c);
}
public Polygone(Point a, Point b, Point c, Point d)
{
this(a, b, c); liste.add(d);
}
public double perimetre()
{
double sum = 0.0;
for(int i=1; i<liste.size(); i++)
{
sum = sum + // À compléter
}
sum = sum + // À compléter;
return sum;
}
"Solution"
public class Polygone
{
private ArrayList<Point> liste;
// Constructeurs (voir indice 1)
public double perimetre()
{
double sum = 0.0;
for(int i=1; i<liste.size(); i++)
{
sum = sum + liste.get(i-1).dist(liste.get(i));
}
sum = sum + liste.get(0).dist(liste.get(liste.size()-1));
return sum;
}
public String toString()
{
String s = "Polygone de " + liste.size() + " sommets";
return s + " de périmètre " + perimetre();
}
}
B-ass-04
Cet exercice fait suite à l’exercice précédent. Vous devez ajouter à la classe Polygone une méthode de classe (static) triangle qui crée et retourne un polygone à trois sommets dont les coordonnées lui sont passées en argument. cette méthode aura donc 6 paramètres de type double.
Vous devez également réaliser une méthode main qui crée une instance de Polygone représentant un triangle en appelant la méthode triangle et qui affiche à l’écran la description de ce triangle obtenue par un appel de la méthode toString de la classe Polygone.
"Indice"
public static Polygone triangle(double x1, double y1, double x2, double y2, double x3, double y3)
{
Point a = // À compléter
Point b = // À compléter
Point c = // À compléter
return new // À compléter
}
public static void main(String[] args)
{
Polygone p = // À compléter
System.out.println(p);
}
La syntaxe la plus stricte pour la deuxième ligne de main devrait être System.out.println(p.toString());. Mais lorsque la référence d’un objet est utilisée à la place d’une chaîne, le compilateur java appelle automatiquement la méthode toString de la classe concernée.
"Solution"
public static Polygone triangle(double x1, double y1, double x2, double y2, double x3, double y3)
{
Point a = new Point(x1, y1);
Point b = new Point(x2, y2);
Point c = new Point(x3, y3);
return new Polygone(a, b, c);
}
public static void main(String[] args)
{
Polygone p = Polygone.triangle(0.0, 0.0, 1.0, 0.0, 0.0, 1.0);
System.out.println(p);
}
B6 : Objets modifiables et non modifiables
Nous revenons ici sur une notion que nous avons déjà abordée sans la nommer dans la partie A. On l’appelle effet de bord. Prenons un exemple avec la classe Date.
public static void effetDeBord()
{
Date d1 = new Date(11,11,1918);
Date d2 = d1;
d2.setAnnee(1919);
System.out.println(d1);
}
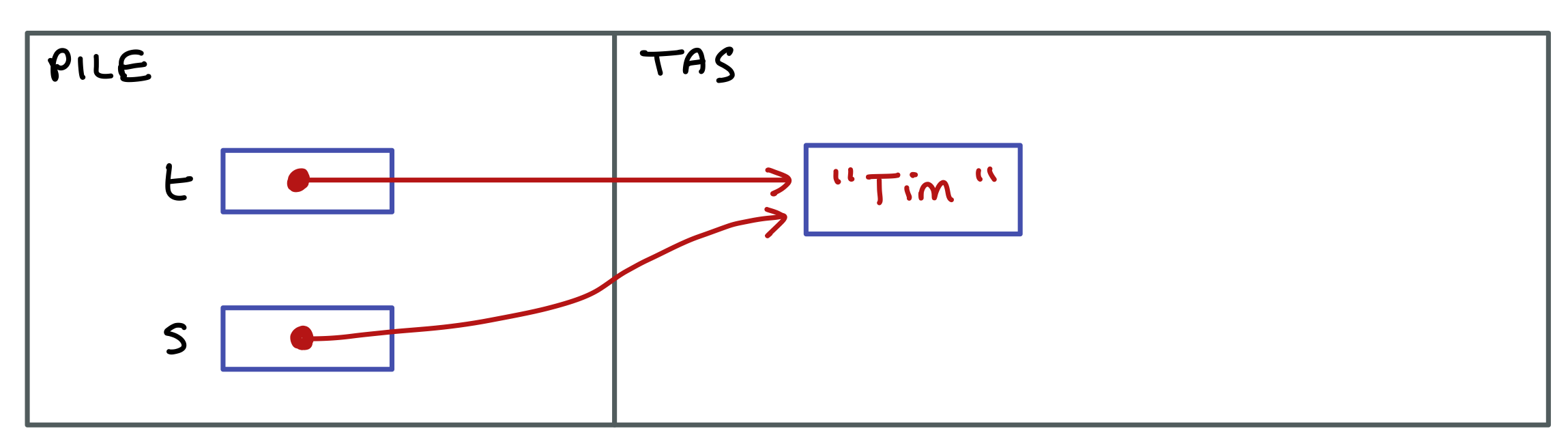
On définit deux variables d1 et d2. On place dans d2 le contenu de d1, puis on change l’année de d2 et on affiche d1. Résultat…
11/11/1919
La modification de la date désignée par d2 a changé aussi celle désignée par d1. Ce n’est pas étonnant quand on regarde la configuration des données en mémoire.
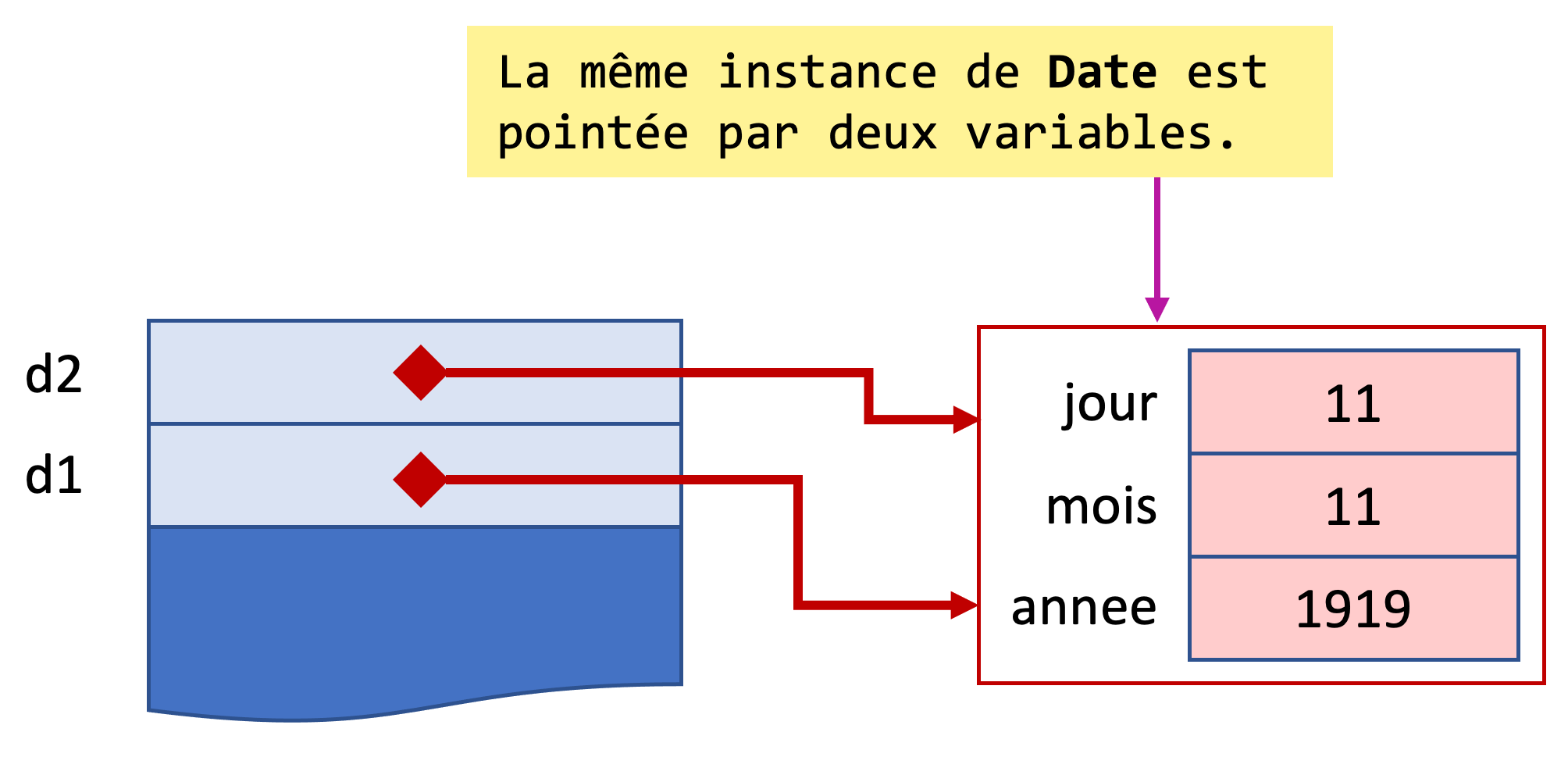
Les deux variables de méthode d1 et d2 contiennent la même référence, qui désigne la même instance de Date.
Pour éviter un tel effet de bord, on peut par exemple doter la classe Date d’un constructeur en copie ou d’une méthode de clonage. Concentrons-nous sur la première solution.
public Date(Date d)
{
this.jour = d.jour;
this.mois = d.mois;
this.annee = d.annee;
}
Voici comment utiliser ce constructeur pour dupliquer une instance de Date.
public static void pasDeffetDeBord()
{
Date d1 = new Date(11,11,1918);
Date d2 = new Date(d1);
d2.setAnnee(1919);
System.out.println(d1);
}
Cette fois-ci, la modification de la date désignée par d2 n’a pas d’effet sur celle désignées par d1. Voici la nouvelle configuration en mémoire.
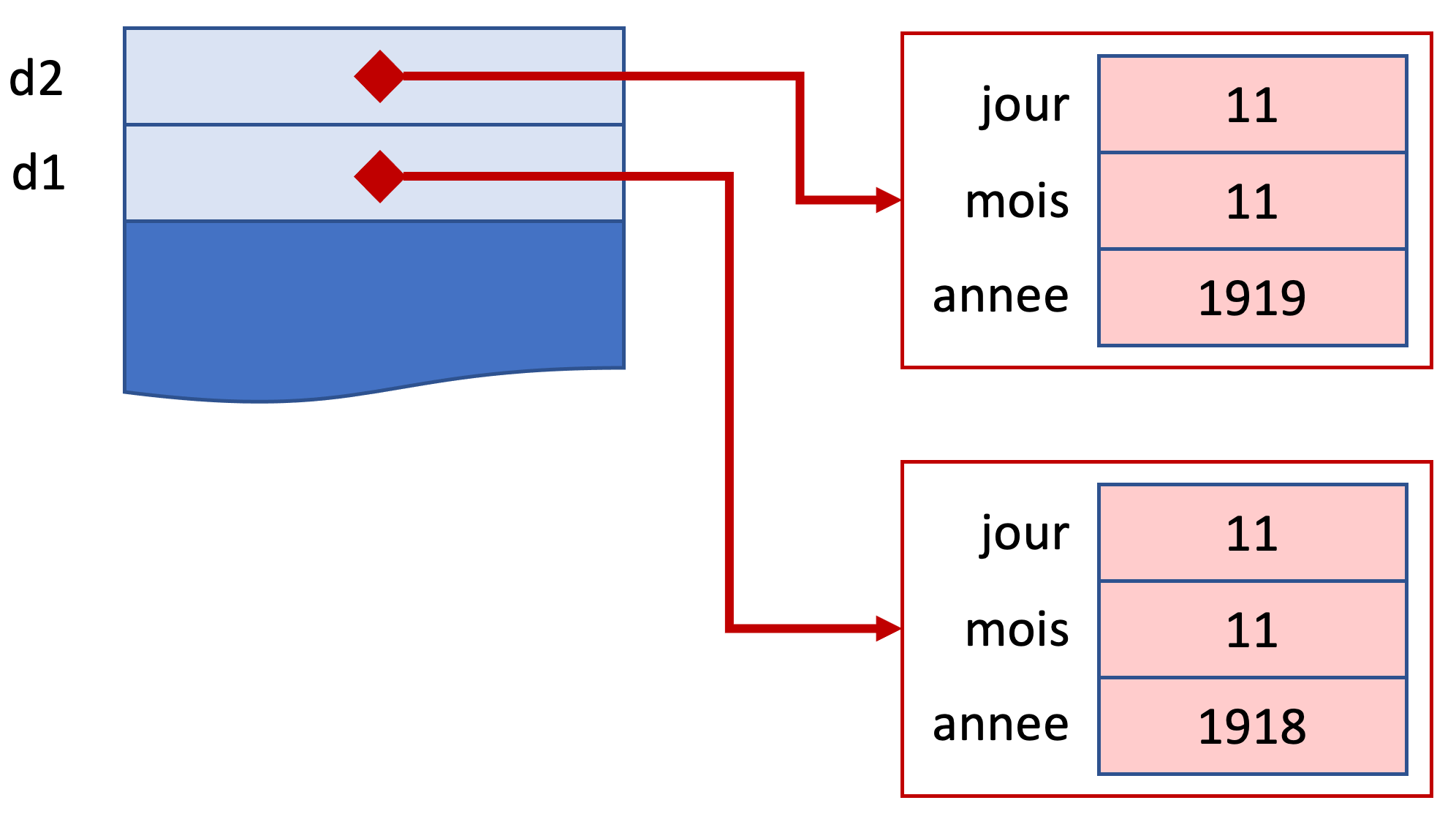
Une autre manière de permettre la duplication d’instance de Date, applicable à toute classe, comme la technique du constructeur en copie, consiste à ajouter à la classe Date une méthode de clonage.
public Date clone()
{
return new Date(this.jour, this.mois, this.annee);
}
Voici un exemple d’utilisation.
public static void pasDeffetDeBord2()
{
Date d1 = new Date(11,11,1918);
Date d2 = d1.clone();
d2.setAnnee(1919);
System.out.println(d1);
}
Exercices de découverte
B-dec-60
Réalisez une méthode d’instance de la classe Date retournant la date située une année plus tard que la date courante, sans modifier la date courante.
public Date plusUnAn()
{
Date cpy = new // À compléter
// À compléter
return cpy;
}
"Solution"
public Date plusUnAn()
{
Date cpy = new Date(this);
cpy.setAnnee(getAnnee()+1);
return cpy;
}
Il y a d’autres solutions valables, telles que celle-ci.
public Date plusUnAn()
{
Date cpy = new Date(this.getJour(), this.getMois(), this.getAnnee() + 1);
return cpy;
}
B-dec-61
Réalisez une variante de la première variante de la méthode d’instance plusUnAn qui utilise la méthode de clonage de la classe Date au lieu de son constructeur en copie.
"Solution"
public Date plusUnAn()
{
Date cpy = clone(); // ou this.clone()
cpy.setAnnee(getAnnee()+1);
return cpy;
}
B7 : Les constantes
Le mot final rend une variable non modifiable et la transforme donc en constante. Sauf que… Examinons un exemple. 
On ne peut pas modifier les références représentées par jours et Armistice, mais cela n’empêche pas de modifier les objets désignés par ces références. Par exemple on peut écrire…
jours[6]="sun";
Armistice.setAnnee(1919);
Ce qui modifiera les objets concernés.
Exercices de découverte
B-dec-70
Pour afficher le nombre $\pi$, on peut écrire :
System.out.println(Math.PI);
Donnez la déclaration de la variable d’instance PI dans le classe Math.
"Solution"
public static final double PI = 3.141592653589793;
B8 : Les classes enveloppes
En java, les types primitifs ne sont pas des objets. Ils constituent une sorte d’entorse au paradigme de programmation objet. Mais il existe des classes enveloppes qui permettent d’encapsuler des données de types primitifs dans des objets : Integer, Double, Boolean… Ces types enveloppe peuvent être utiles pour utiliser des données primitives dans de situation où seuls des objets sont utilisables, comme dans des ArrayList. Voici un exemple.
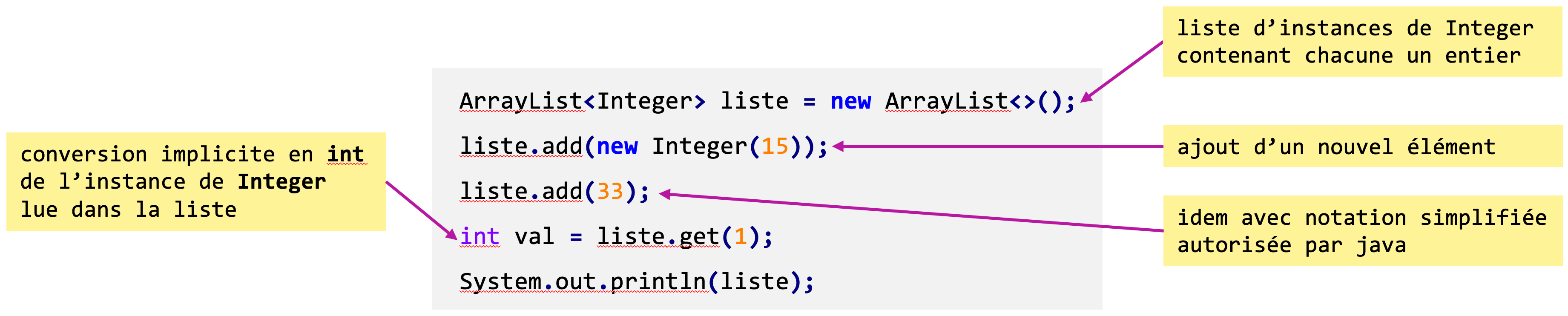
Exercices de découverte
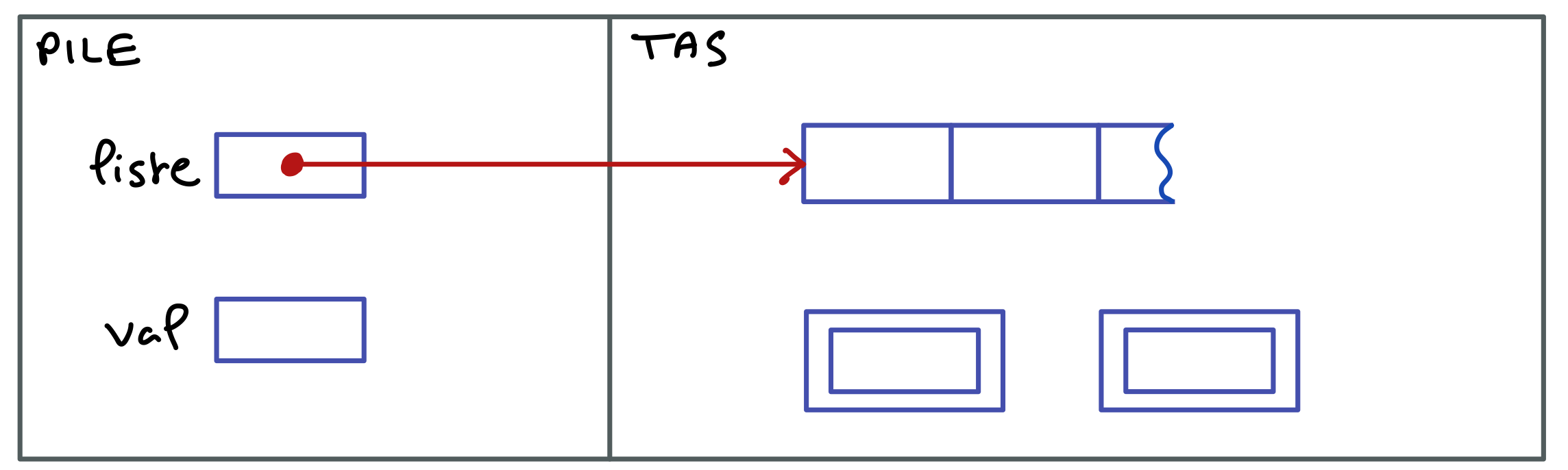
B-dec-80
Complétez cette illustration de la configuration en mémoire à l’issue de l’exécution des 4 premières lignes de code de l’exemple précédent.
B9 : Objets non modifiables
Les objets n’ayant que des attributs privés et ne disposant pas de méthodes permettant de modifier leurs attributs (ni les données accessibles par ces attributs) sont dits non modifiables, tout comme les classes qui définissent de tels objets.
Par exemple, les classes enveloppes sont non modifiables, ainsi que la classe String. L’intérêt de telles classes c’est qu’elles empêchent les effets de bord, mais en contrepartie d’une perte d’efficacité. On peut le voir en considérant deux classes permettant de représenter des chaînes : String, qui est non modifiable, et StringBuffer, qui est modifiable.
La méthode de classe suivante…
public static String makeString1(String s, int n)
{
String r = "";
for(int i=0; i<n; i++)
{
r = r + s;
}
return r;
}
…permet de construire une chaîne par n concaténations successives d’une chaîne s. Par exemple…
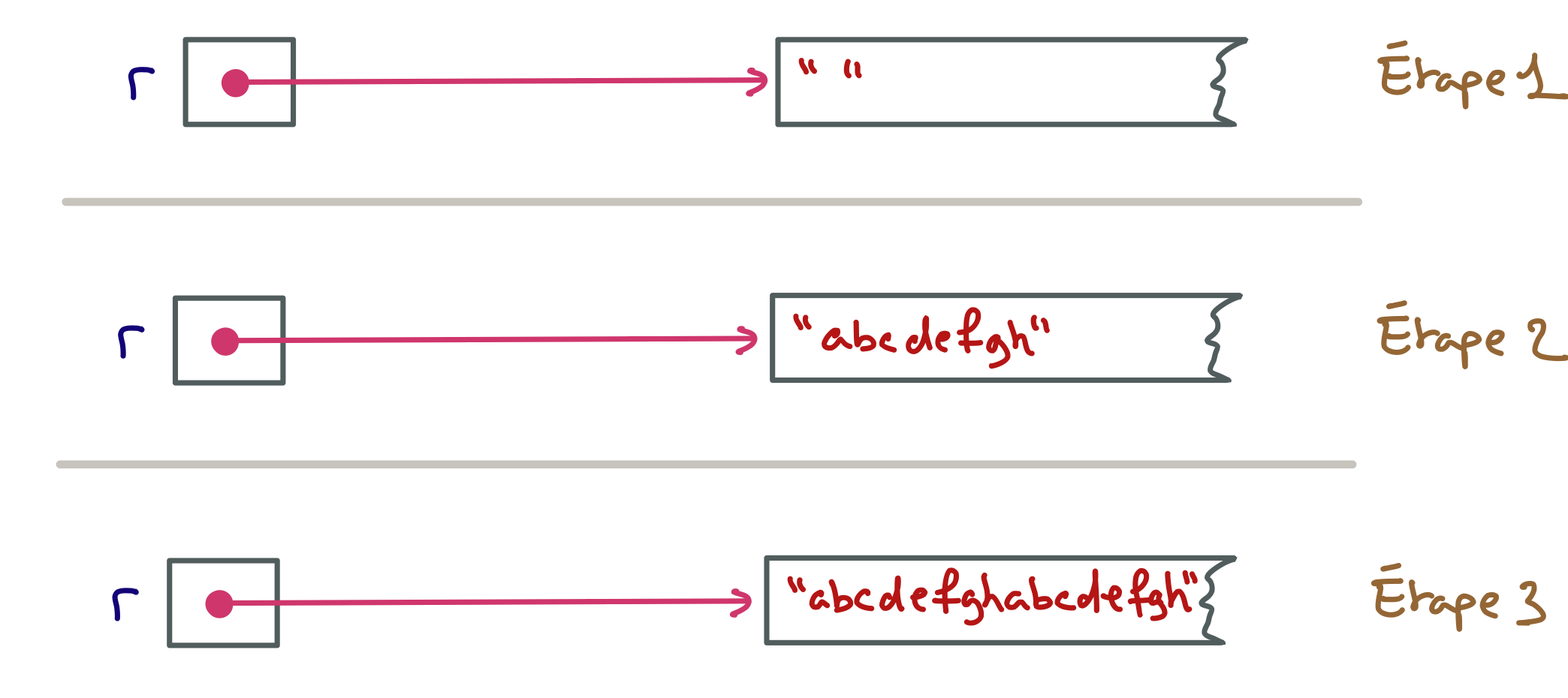
System.out.println(makeString1("abcdefgh",10));
… affiche…
abcdefghabcdefghabcdefghabcdefghabcdefghabcdefghabcdefghabcdefghabcdefghabcdefgh
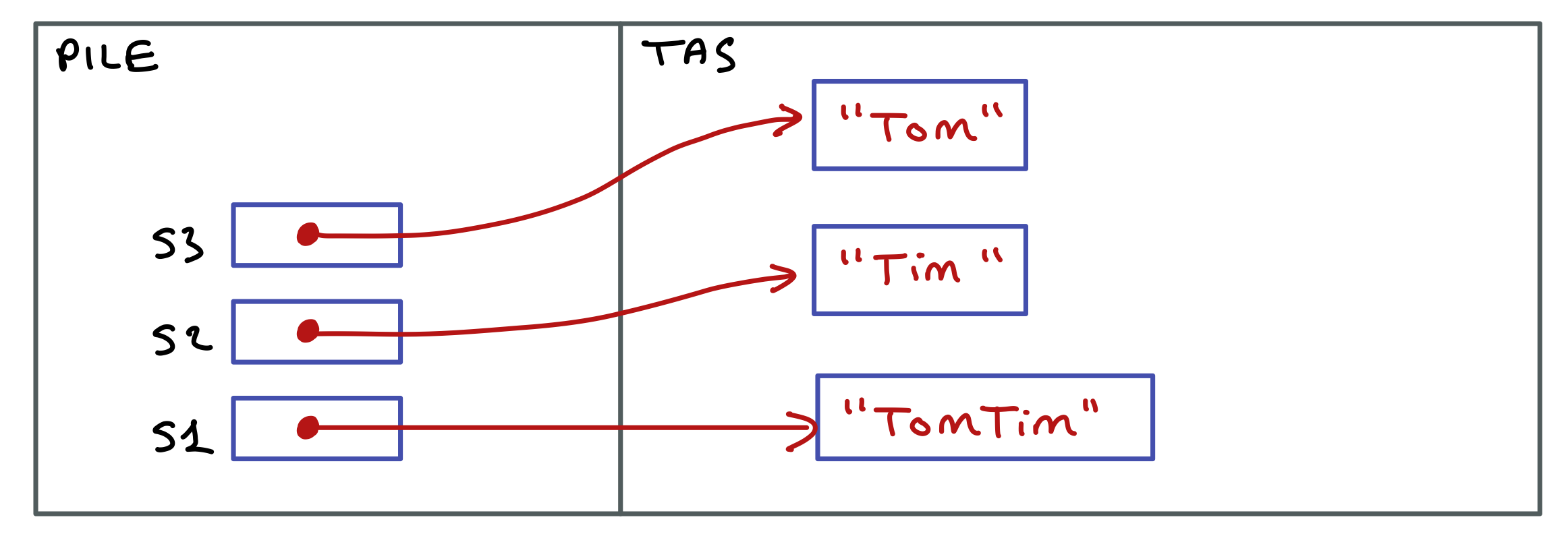
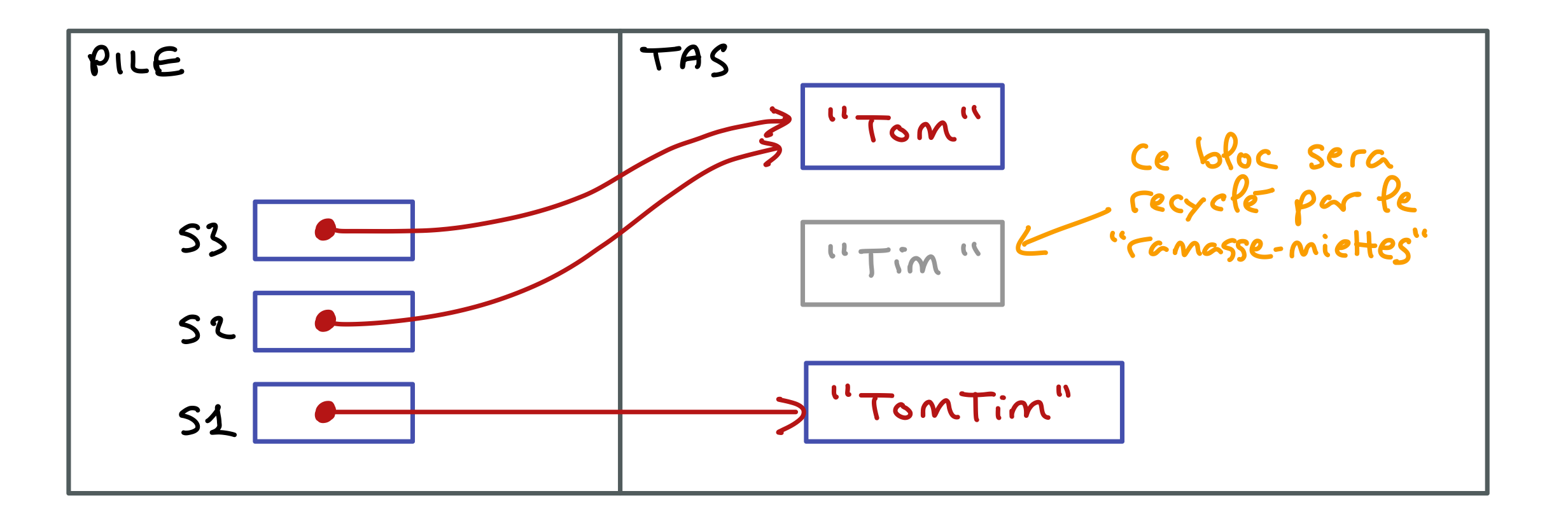
Mais cette méthode n’est pas très efficace. Pour fabriquer la chaîne retournée, cette méthode crée successivement n nouvelles chaînes intermédiaires qui sont ensuite recyclées par le ramasse-miettes de la machine virtuelle. En effet, chaque concaténation réalisée par l’opérateur + ne modifie pas une chaîne existante (puisque les chaînes sont des objets non modifiables) mais en crée une nouvelle.
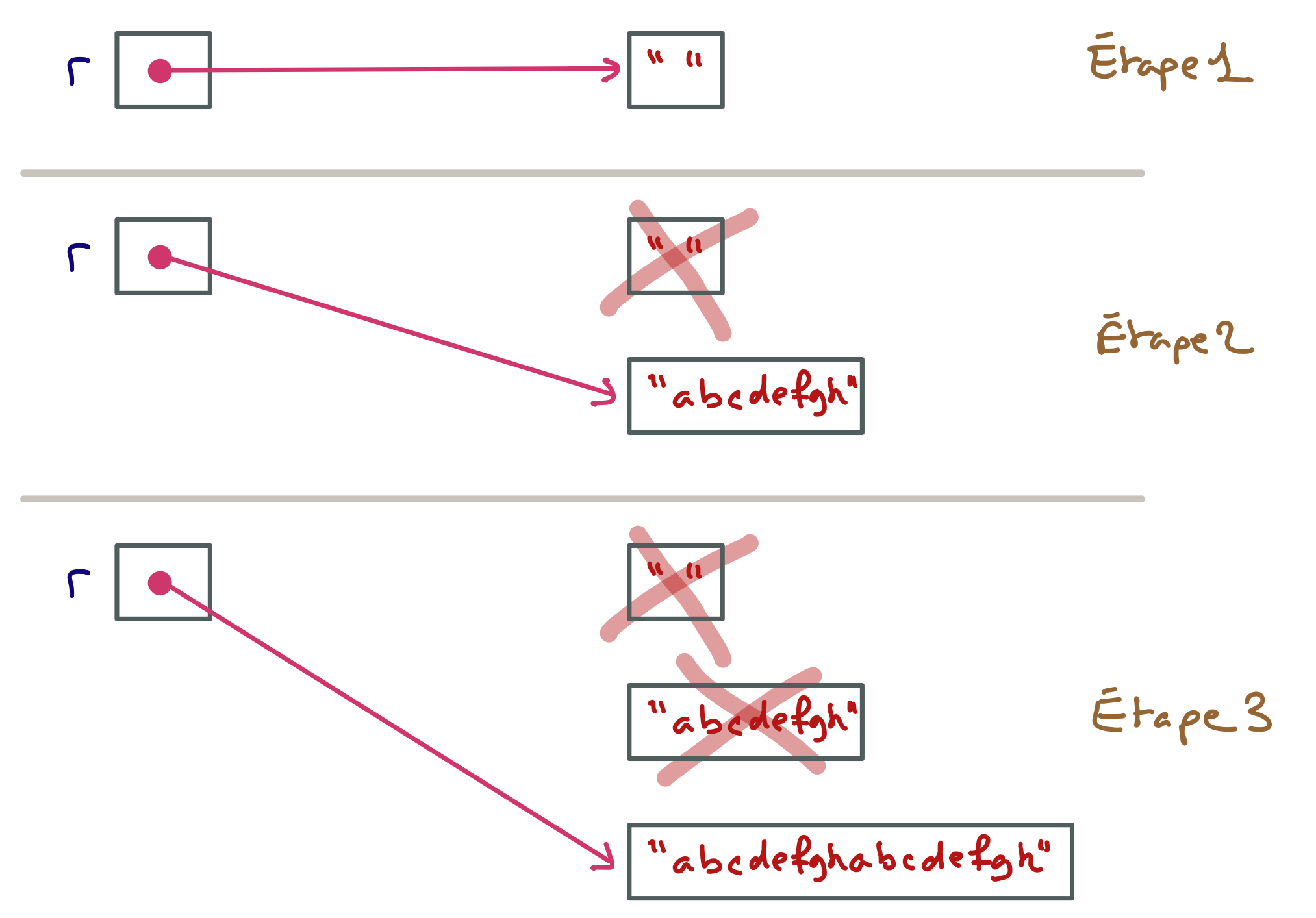
On peut réaliser la même chose en utilisant la classe modifiable StringBuffer qui dispose d’une méthode append permettant d’ajouter une chaîne à la fin de la chaîne courante sans en recréer une nouvelle.
public static String makeString2(String s, int n)
{
StringBuffer r = new StringBuffer();
for(int i=0; i<n; i++)
{
r.append(s);
}
return r.toString();
}
Lors de la création d’une instance de StringBuffer, une certaine ressource de mémoire est réservée pour le stockage de la chaîne courante. Cette quantité de mémoire est augmentée en fonction des besoins.
Exercices de découverte
B-dec-90
À quoi peut-on reconnaître une classe non modifiable en regardant son code ?
"Solution"
Une classe est non modifiable si et seulement si aucune de ses méthodes ne permet de changer la valeur d’un des attributs d’un objet après sa création.
Exercices d’assimilation
B-ass-50
Réalisez un constructeur en copie pour la classe Memo (en version ArrayList comme demandé par l’exercice 2). Ce constructeur doit accepter en paramètre une instance de Memo déjà créée et faire en sorte que l’instance construite soit identique, mais que toute modification de la copie créée (ajout ou modification d’une date) n’affecte pas l’original et réciproquement.
"Indice
public Memo(Memo m)
{
this(); // Pour créer la liste vide
for(int i=0; i<tab.size(); i++)
{
tab.add(// À compléter);
}
}
"Indice
public Memo(Memo m)
{
this();
for(int i=0; i<tab.size(); i++)
{
tab.add( new Date(// À compléter) );
}
}
Il est important de créer de nouvelles instances de Date identiques à celles qui sont dans le mémo servant de modèle. Si on plaçait dans la liste du nouveau mémo les références des dates du mémo servant de modèle, une modification d’une de ces dates affecterait les deux mémos, parce que Date est une classe modifiable. Le problème ne se poserait pas si c’était une classe non modifiable.
"Solution"
public Memo(Memo m)
{
this();
for(int i=0; i<tab.size(); i++)
{
tab.add( new Date(m.tab.get(i)) );
}
}
Voici une variante qui fonctionne aussi avec un code un peu plus propre.
public Memo(Memo m)
{
this();
for(Date e : tab)
{
tab.add( new Date(e) );
}
}
Il serait encore plus conforme aux bonnes pratiques de mettre dans la classe Memo une méthode permettant de récupérer la date située à une position passée en argument, et d’utiliser cette méthode au lieu d’accéder à l’attribut tab. Toutefois, l’accès à cet attribut privé est parfaitement légal puisque le modificateur d’accès private privatise un attribut dans le scope d’une classe et non de chacune des instances de cette classe : une méthode d’instance peut accéder aux attributs privés d’une autre instance, si elle a accès la référence de cette autre instance.
B-ass-51
Ajoutez à la classe Polygone une méthode…
public Polygone ext(Point p)
…qui produit un nouveau polygone constitué des points du polygone courant plus le point désigné par le paramètre p. L’ancien et le nouveau polygone doivent exister indépendamment l’un de l’autre. Pour rendre le code plus lisible, vous devrez définir un constructeur en copie de la classe Polygone, qui doit appeler le constructeur par défaut de cette classe. Notez que la classe Point n’est pas modifiable.
"Indice"
Voici un constructeur en copie pour la classe Polygone.
public Polygone(Polygone m)
{
this();
for(Point p : m.liste)
{
liste.add(p);
}
}
Il reste à écrire la méthode ext.
"Solution"
// Constructeur en copie donné dans l'indice 1
public Polygone ext(Point p)
{
Polygone poly = new Polygone(this);
poly.liste.add(p);
return poly;
}
Exercices d’approfondissement
B-cons-00
Vous devez développer un programme permettant de simuler un système d’offres par soumissions cachetées pour l’achat d’objets identiques. Il y a N objets en vente. Il peut y avoir plus (ou moins, ou autant) d’acheteurs intéressés que d’objets en vente. Chaque acheteur peut faire une ou plusieurs offres qui ne sont pas connues par les autres acheteurs. Les N meilleures offres seront retenues.
Chaque offre est représentée par une instance de la classe Offre suivante.
public class Offre
{
public int id;
public double montant;
public Offre(int id, double montant)
{
this.id = id; this.montant = montant;
}
public int getId() {return id;}
public double getMontant() {return montant;}
public String toString()
{
return "[ " + id + " : " + montant + "]";
}
}
Les offres sont placées dans une instance de la classe PrioFile, que vous devez implémenter. Une telle instance est appelée file de priorité. Elle contient une liste d’offres. Pour créer une file de priorité, on écrit…
PrioFile file = new PrioFile(n);
…où nest le nombre d’objets en vente. La file de priorité créée comportera au plus n offres, chacune représentée par une instance de la classe Offre. Tant que la file contient moins de n offres, chaque nouvelle offre y est automatiquement ajoutée. Au delà, quand une nouvelle offre est proposée, elle n’est ajoutée que si son montant dépasse celui de l’offre la plus récente parmi celles ayant le plus petit montant.
Pour soumettre une offre, on écrit…
file.soumission(id, montant);
…où id est l’identifiant d’une acheteur potentiel et montant est le montant proposé.
La classe PrioFile dispose d’une méthode toString qui affiche la liste complète des offres retenues.

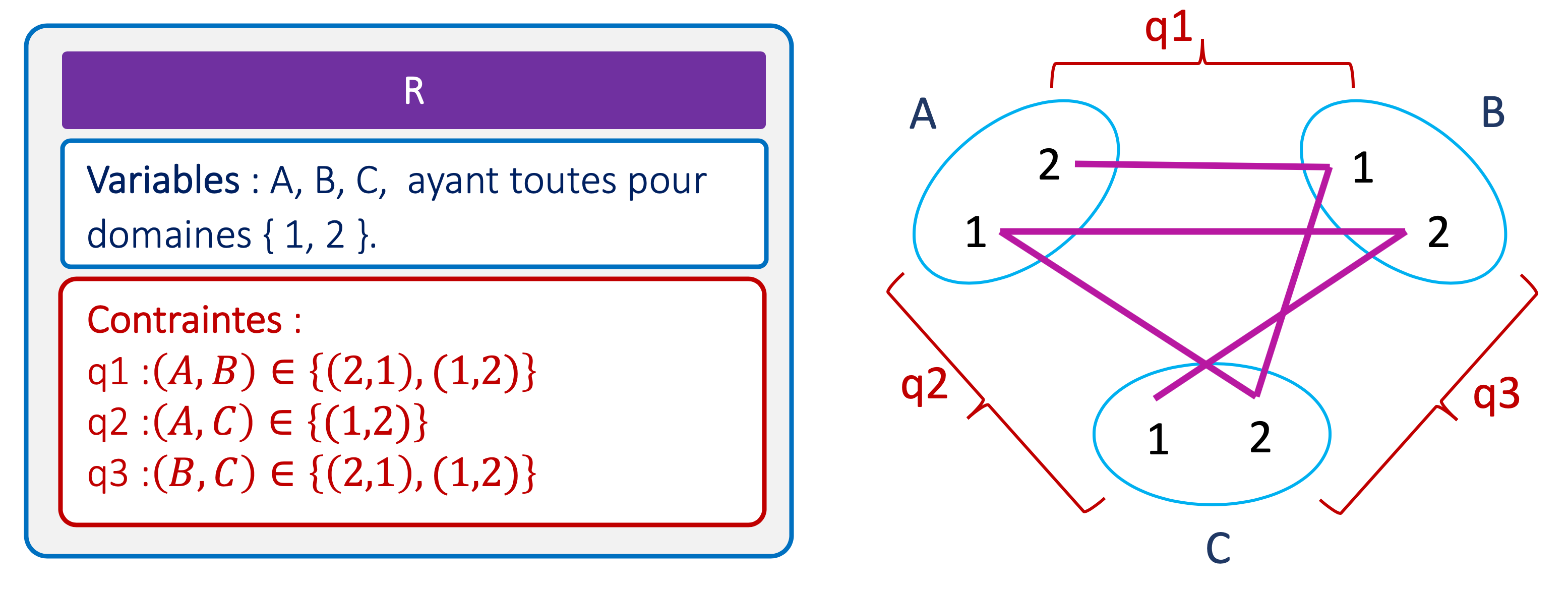
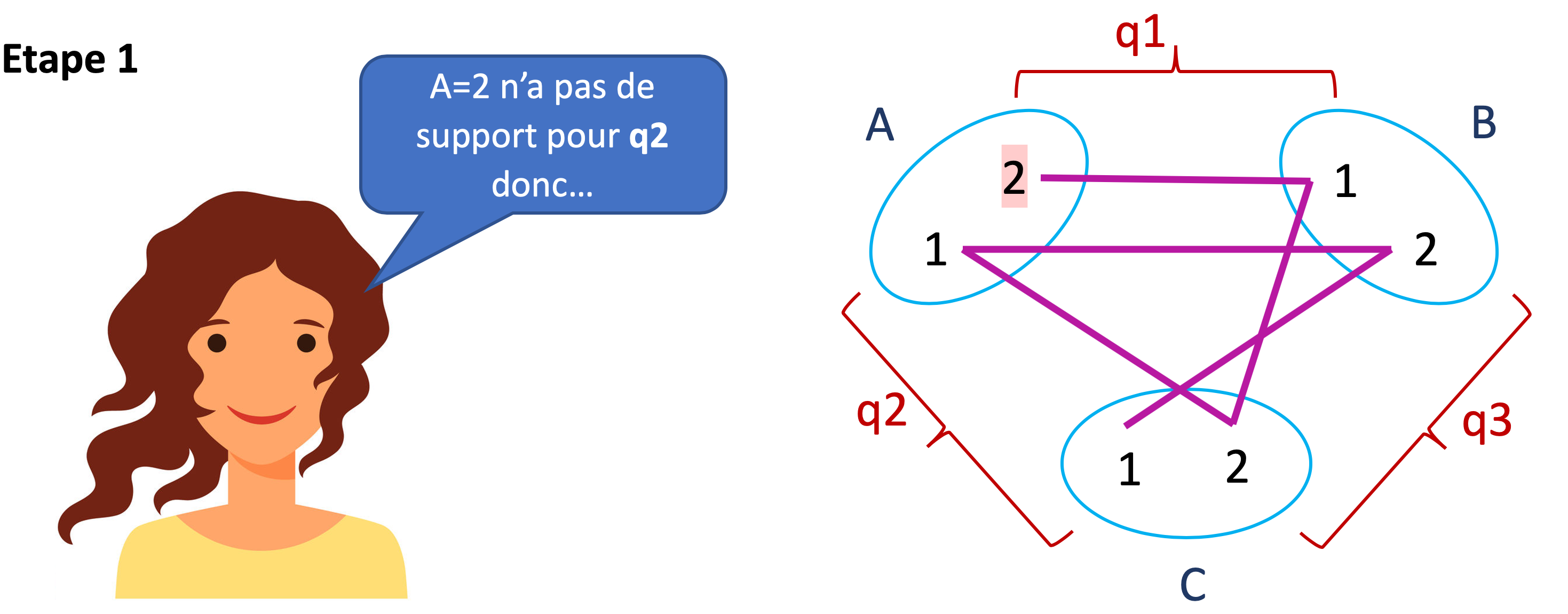

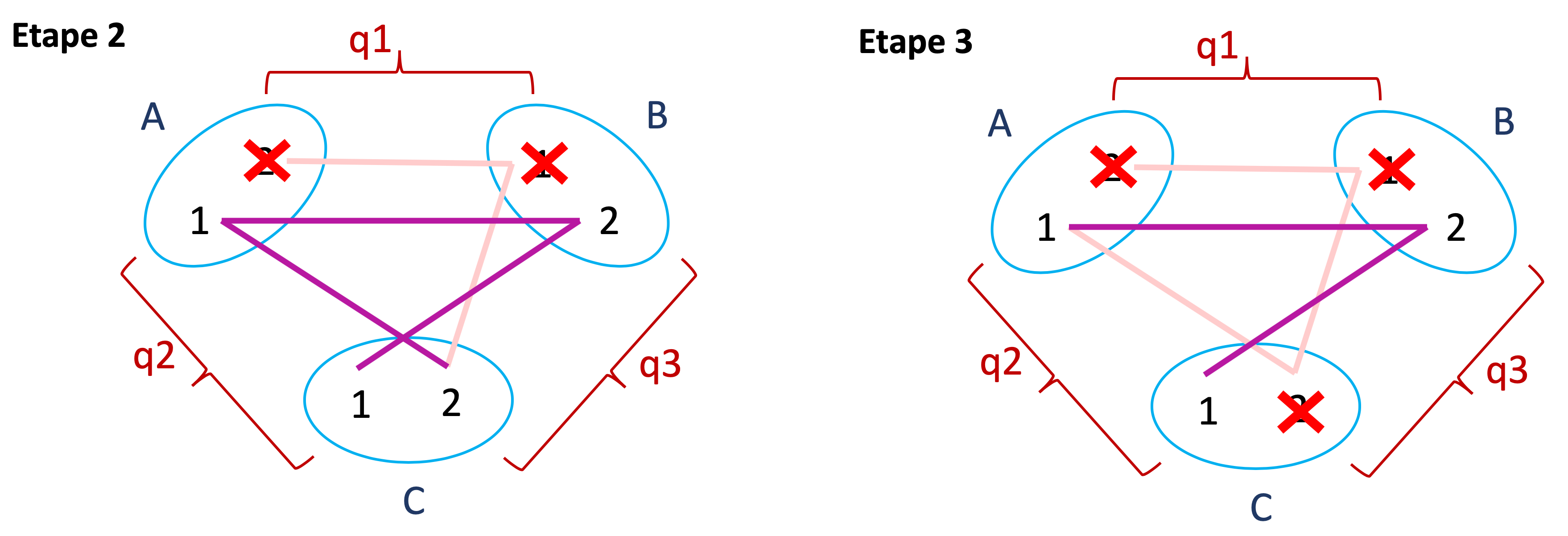
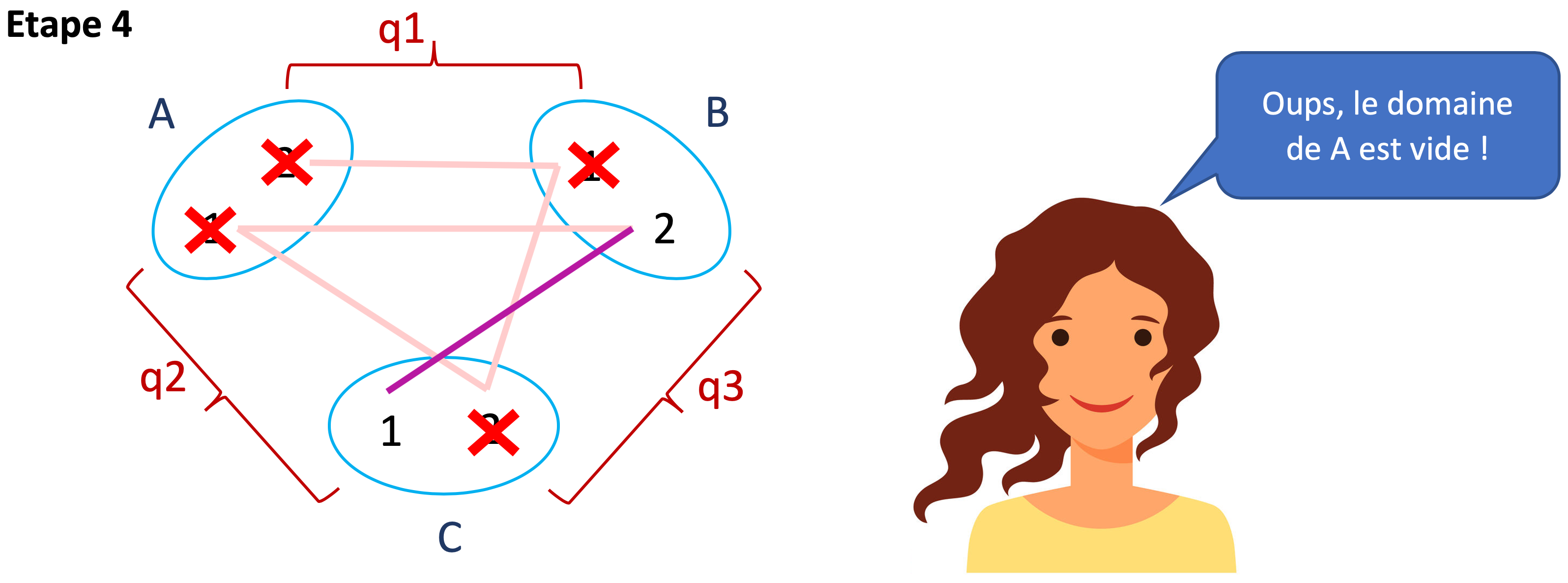


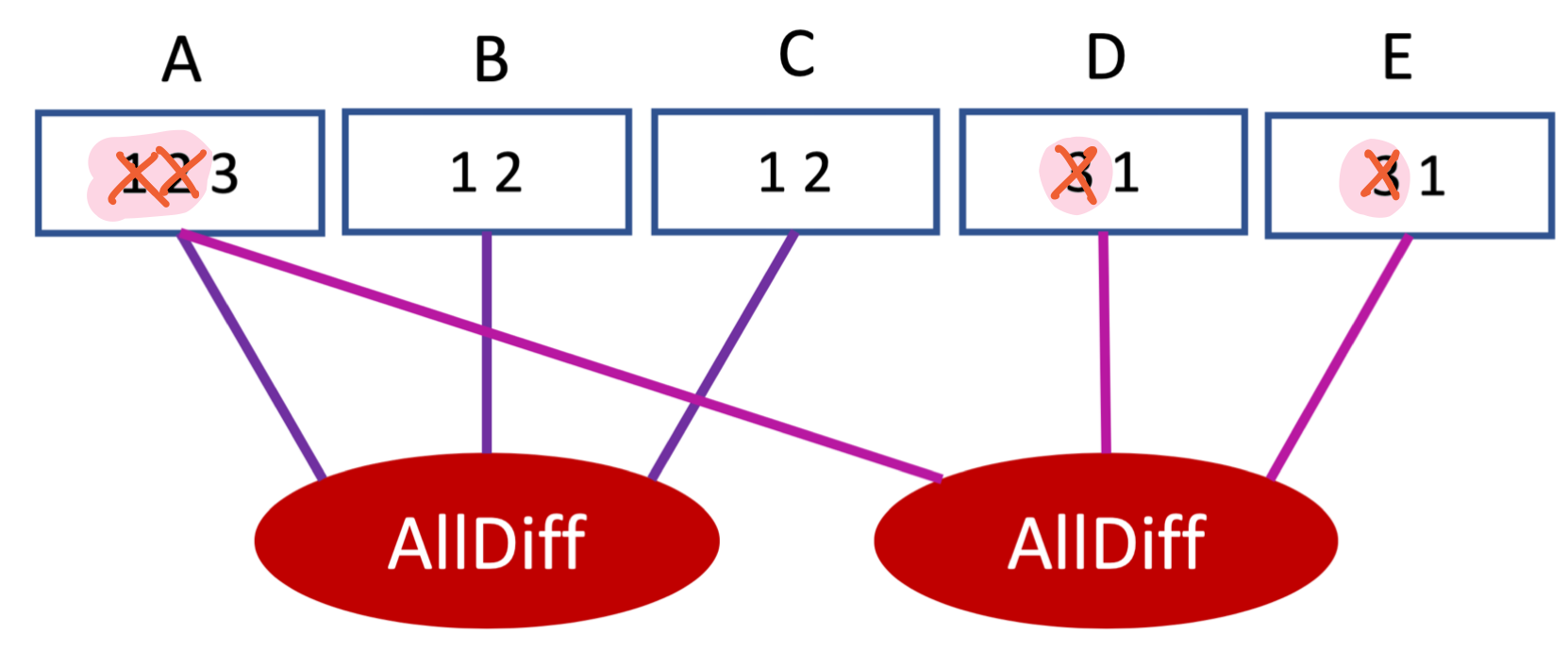
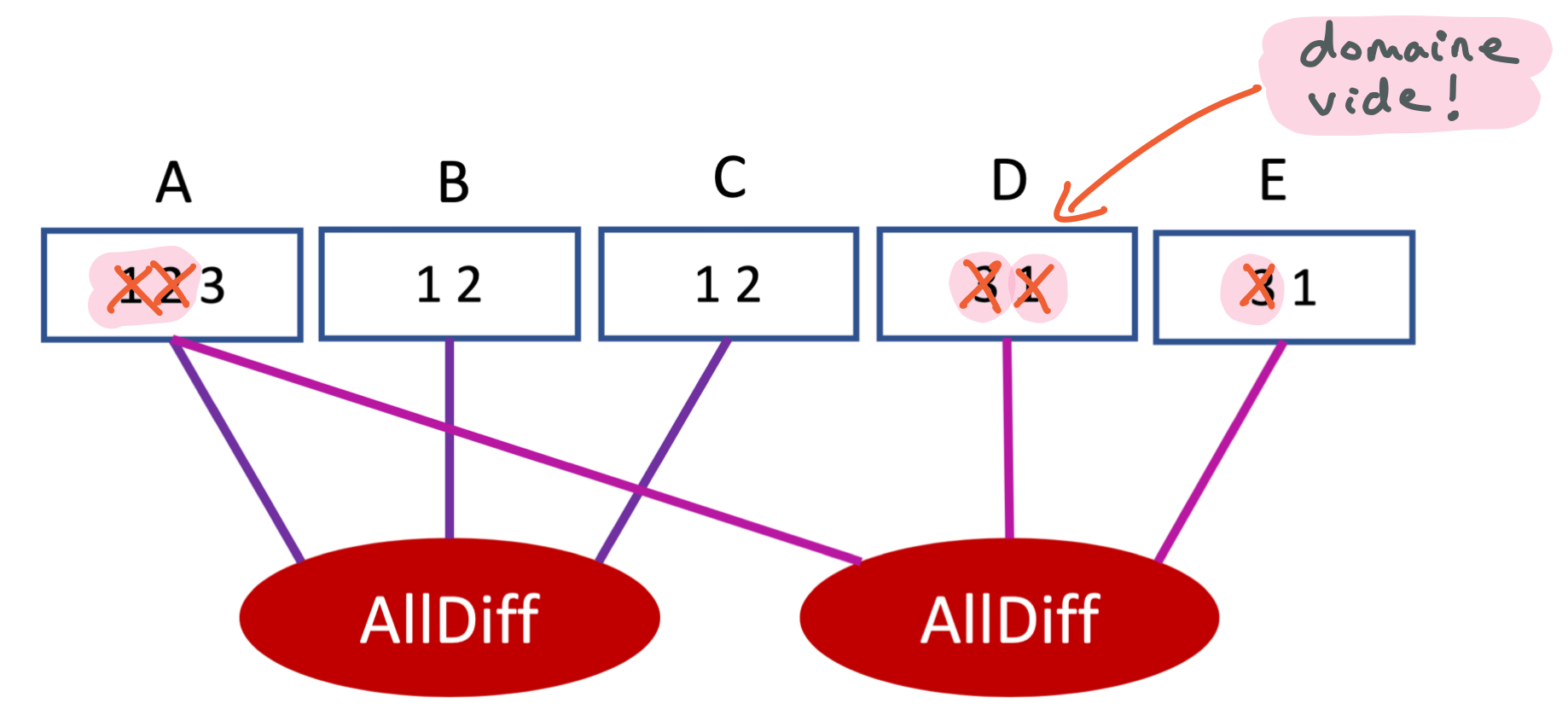
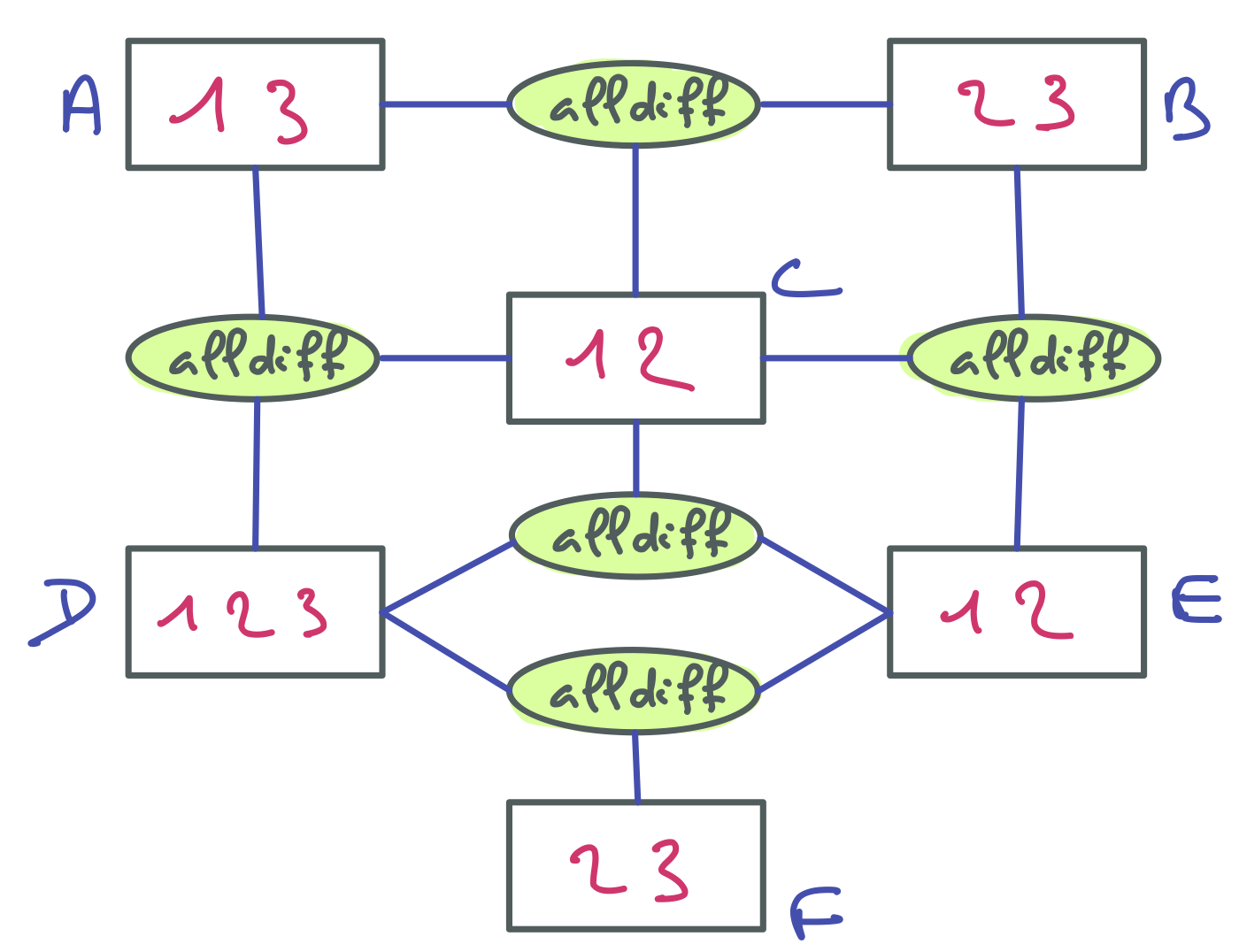
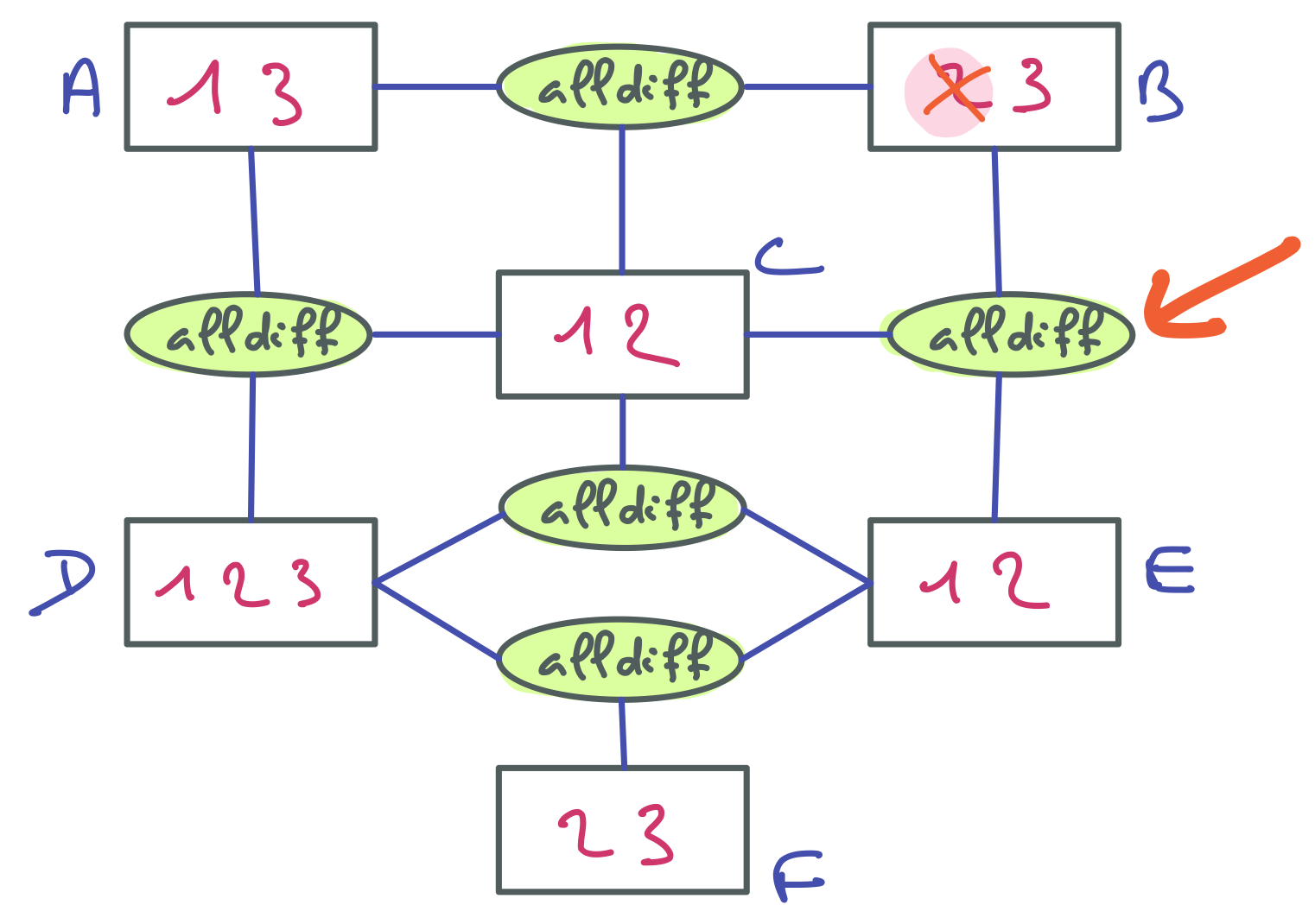
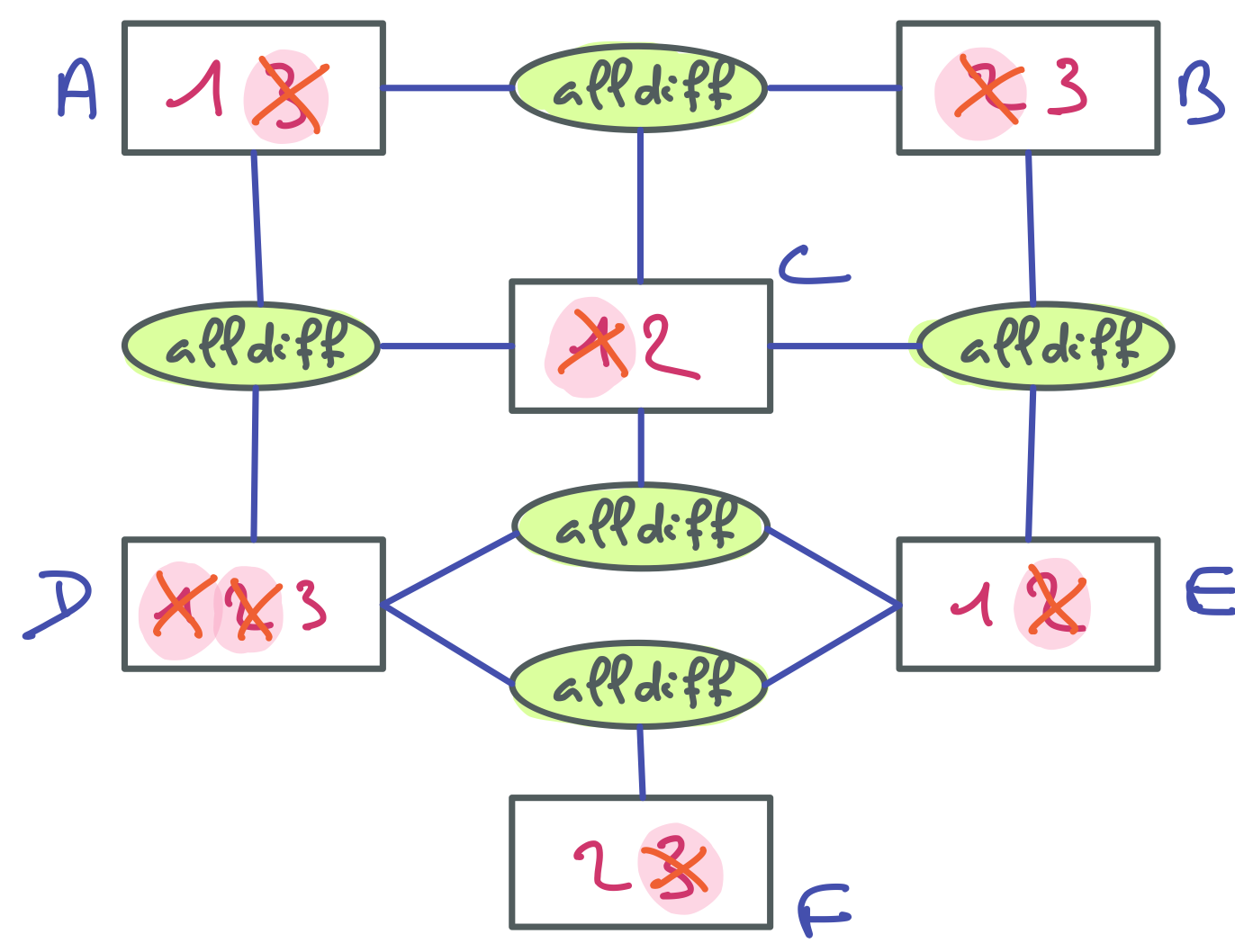
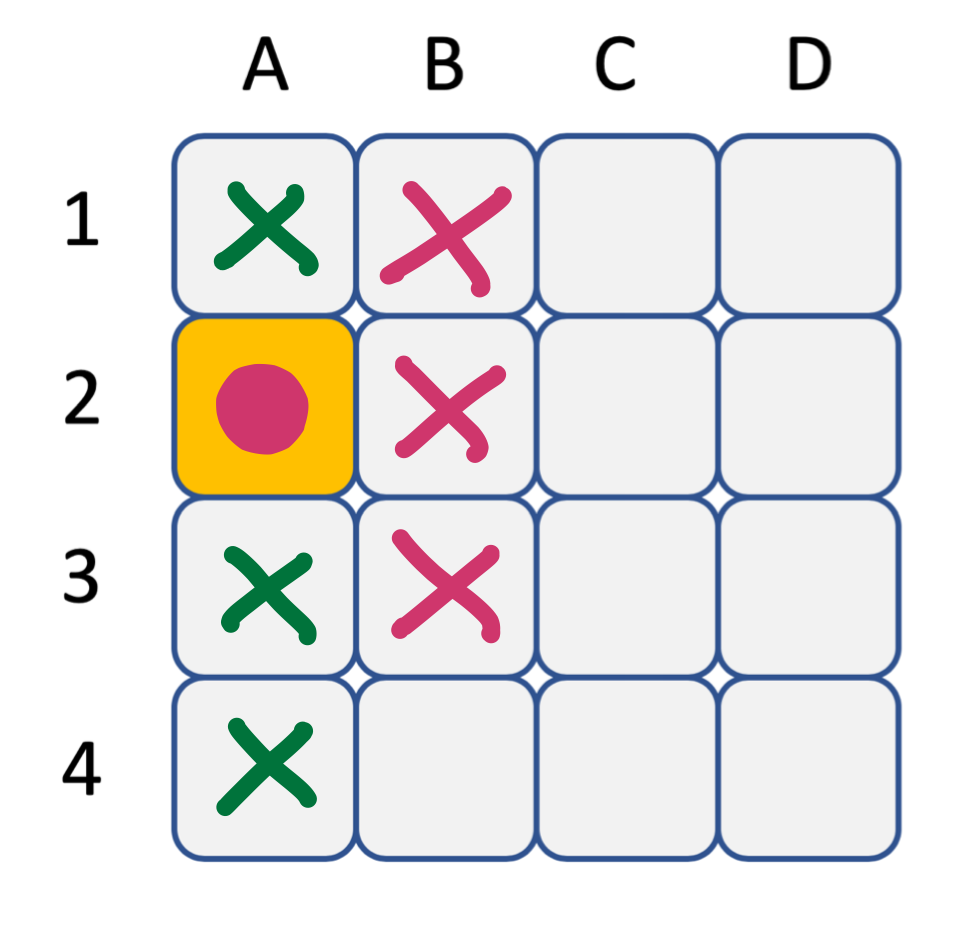 A étant assignée à 2, les cases correspondant aux autres valeurs du domaine de A ont été barrées. On voit facilement les valeurs de B qui doivent être retirées. Elles correspondent aux cases menacées par la reine située sur la première colonne. Du coup, il ne reste que 4 dans le domaine de B, ce qui revient à assigner B=4. Pour la suite, merci de visiter la contrainte entre A et C pour que les indices suivants soient pertinents.
A étant assignée à 2, les cases correspondant aux autres valeurs du domaine de A ont été barrées. On voit facilement les valeurs de B qui doivent être retirées. Elles correspondent aux cases menacées par la reine située sur la première colonne. Du coup, il ne reste que 4 dans le domaine de B, ce qui revient à assigner B=4. Pour la suite, merci de visiter la contrainte entre A et C pour que les indices suivants soient pertinents.