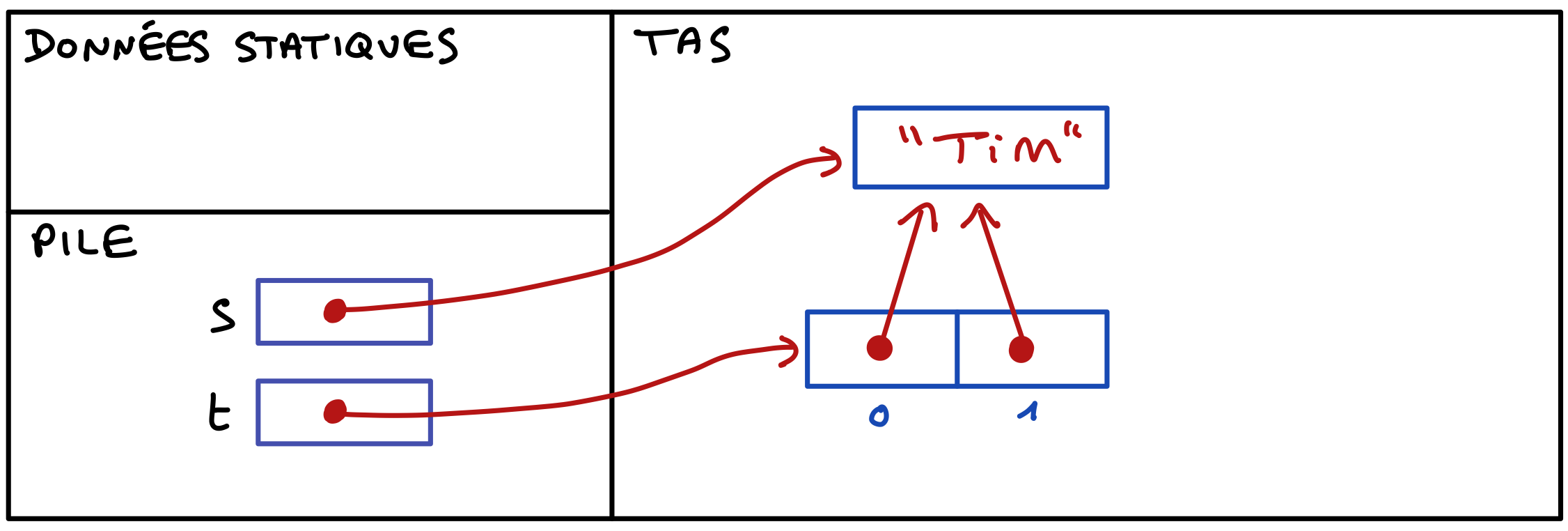
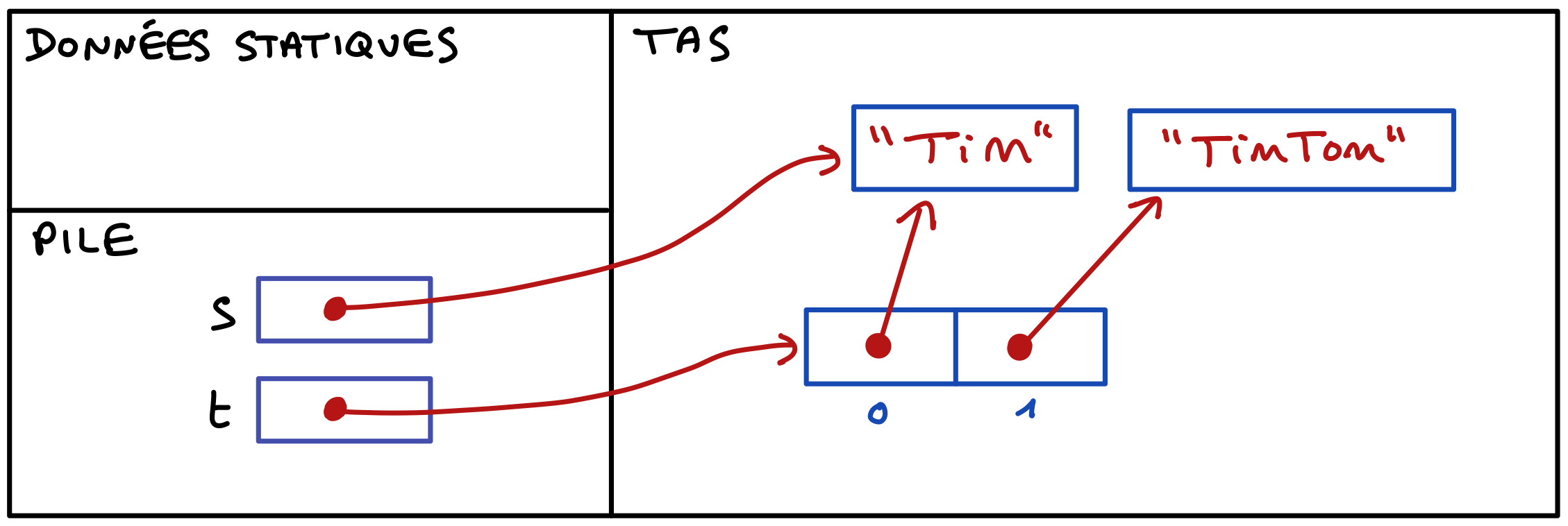
Partie D : Les exceptions
Objectif
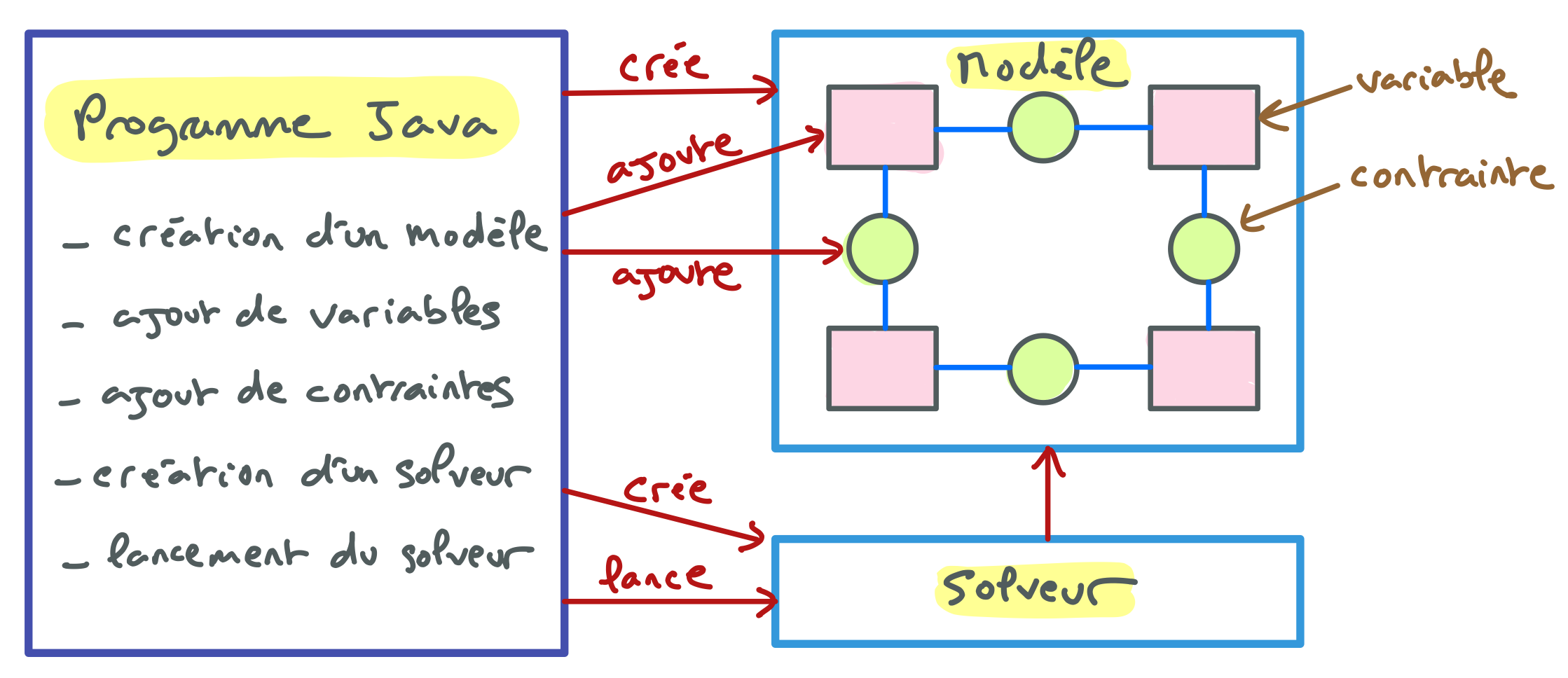
Être capable d’implémenter au sein d’une application telle que celles décrites dans les objectifs des parties B et C une gestion des exceptions : implémentation de classes d’exception, levée et interception d’exceptions. Être capable de prévoir le comportement d’un programme dans lequel des exceptions peuvent être produites et interceptées.
Prérequis
Partie C
D1 : Lancer et gérer une exception
Java permet à une méthode ou un constructeur de lancer une exception lorsqu’une situation particulière se produit lors de son exécution. Une exception est un objet, plus précisément une instance d’une classe dérivant de la classe prédifinie Exception.
Nous allons découvrir ce ce concept avec un exemple. La classe ci-dessous représente une liste de notes obtenues par un élève à une unité d’enseignement.
public class SuiviUE
{
private String idUE; //Intitulé de l'UE
private double coeff; //Coefficient
private ArrayList<Double> notes;
public SuiviUE(String nom, double coeff)
{
this.coeff = coeff;
this.idUE = nom;
this.notes = new ArrayList<>();
}
public void add(double note)
{
notes.add(note);
}
public String toString()
{
return "UE : " + idUE + " coefficient : " + coeff
+ " notes " + notes;
}
}
On y trouve un constructeur créant une liste de note vide, une méthode pour ajouter une note, et une méthode pour afficher une description de l’instance courante. Une schéma très classique qui correspond aux compétences introduites dans la partie B du cours.
A titre d’exercice de rappel, ajoutez à la classe SuiviEU une méthode moyenne qui calcule et retourne la moyenne des notes situées dans la liste.
"Solution"
public double moyenne()
{
double sum = 0.0;
for(double x : notes) sum += x;
return sum / notes.size();
}
Faisons maintenant l’expérience suivante, qui consiste à calculer la moyenne d’une instance de suiviUE à laquelle aucune note n’a été ajoutée.
public class Main
{
public static void main(String[] args)
{
SuiviUE r = new SuiviUE("Java", 2.0);
System.out.println(r.moyenne());
}
}
On obtient l’affichage…
NaN
…qui signifie "Non Arithmetic Number". C’est ce qui se produit, dans beaucoup de langages de programmation, lors d’une tentative de division par 0 d’un nombre flottant (de type double).
Nous allons changer ce comportement en faisant en sorte que lorsqu’il n’y a pas de note, une exception soit levée, puis nous allons montrer comment exploiter cette exception. Mais pour commencer, il nous faut une classe dérivant de Exception.
public class Defaillance extends Exception
{
private String id;
public Defaillance(String ue)
{
//super(); // ligne A
this.id = ue;
}
public String getID()
{
return id;
}
}
Cette classe ne comporte pas d’attribut (mais on pourrait lui en ajouter si nécessaire) ni de méthode (mais on pourrait aussi en ajouter en cas de besoin). Son constructeur, qui permet de créer un objet de type exception, fait appel à un constructeur de la superclasse Exception qui accepte en argument une chaîne de caractères. Cette chaîne pourra être récupérée avec la méthode toString héritée de la classe Exception.
Si on enlève la mise en commentaire de la ligne A, le constructeur par défaut de la superclasse Exception est appelé explicitement, alors que sinon il est appelé implicitement, ce qui en pratique ne change rien.
Voici une nouvelle version de la méthode moyenne qui lève une exception de type Defaillance lorsque la liste de notes est vide.
public double moyenne() throws Defaillance // ligne A
{
if(notes.size() == 0)
{
throw new Defaillance(idUE); // ligne B
}
double sum = 0.0;
for(double x : notes) sum += x;
return sum / notes.size();
}
Deux nouveaux mot-clés importants apparaissent ici :
throws permet de dire au compilateur java que la méthode moyenne est susceptible de produire une exception du type indiqué. Il est possible d’indiquer ici plusieurs types d’exceptions.throw permet de lever (lancer, produire) une exception et doit être suivi par une instance d’exception, généralement produite avec new et un constructeur d’une classe d’exception.
À chaque fois qu’une méthode susceptible de lancer une exception est appelée par une méthode m, la méthode m doit :
- soit intercepter l’exception et la gérer,
- soit la remonter à la méthode ayant appelé m.
Nous allons illustrer le premier cas.
public class Main
{
public static void main(String[] args)
{
SuiviUE r = new SuiviUE("Java", 2.0);
// r.add(12.0); r.add(17.0); // ligne A
try // ligne B
{
System.out.println(r.moyenne());
}
catch(Defaillance d) // ligne C
{
System.out.println("Défaillance à l'UE : " + d.getID());
return;
}
System.out.println(r);
}
}
L’instruction try … catch permet d’intercepter les exceptions d’un ou plusieurs types qui se produisent dans le bloc de code try et et définir les actions à réaliser si de telles exceptions se produisent. Il peut y avoir plusieurs blocs catch permettant de spécifier des traitement spécifiques à différents types d’exceptions susceptibles de se produire lors de l’exécution du code du bloc try.
À l’issue de l’exécution du try catch, l’exécution du code de la méthode reprend son cours, qu’il y ait eu exception ou pas, sauf si le traitement d’une exception a mis fin à cette exécution par une instruction return, ce qui est le cas dans l’exemple.
Exercices de découverte
D-dec-10
Tentez de déterminer ce que va afficher le programme d’exemple ci-dessus, en prenant en compte que la ligne A est un commentaire, qui ne s’exécutera pas.
"Solution"
Défaillance à l'UE : Java
D-dec-11
Tentez de déterminer ce que va afficher le programme d’exemple ci-dessus si on retire la mise en commentaire de la ligne A.
"Solution"
14.5
UE : Java coefficient : 2.0 notes [12.0, 17.0]
D-dec-12
Tentez de déterminer ce que va afficher le programme d’exemple ci-dessus si on remet en commentaire la ligne A, comme dans l’exercice D-dec-10, et qu’on supprime le return.
"Solution"
Défaillance à l'UE : Java
UE : Java coefficient : 2.0 notes []
D-dec-13
On remplace la ligne C par :
catch(Exception d) // ligne C
On refait les expériences décrites dans les trois exercices précédentes et on obtient exactement les mêmes résultats. Pourquoi ?
"Solution"
Comme la classe Defaillance hérite de la classe Exception, toute instance de Defaillance est aussi une instance de Exception et sera donc capturée.
D2 : Plus loin avec les exceptions
Dans la section précédente, nous avons introduit une classe SuiviUE qui représente une liste de notes attribuées à un même élève (non désigné) pour une même unité d’enseignement identifiée par une chaîne de caractères et à laquelle est associé un coefficient.
Dans cette section, nous reprenons la même classe mais avec une petite modification : les attributs n’ont plus les droits d’accès private mais par défaut, c’est à dire qu’ils sont accessibles depuis toutes les classes du package dans lequel se trouve la classes SuiviUE.
public class SuiviUE
{
String idUE; //Intitulé de l'UE
double coeff; //Coefficient
ArrayList<Double> notes;
public SuiviUE(String nom, double coeff)
{
this.coeff = coeff;
this.idUE = nom;
this.notes = new ArrayList<>();
}
public void add(double note)
{
notes.add(note);
}
public String toString()
{
return "UE : " + idUE + " coefficient : " + coeff
+ " notes " + notes;
}
public double moyenne() throws Defaillance
{
if(notes.size() == 0)
{
throw new Defaillance(idUE);
}
double sum = 0.0;
for(double x : notes) sum += x;
return sum / notes.size();
}
}
Nous allons ajouter à ce package une nouvelle classe SuiviEtu qui représente les notes d’un même élève, identifié par un numéro, dans plusieurs unités d’enseignement. Les notes de cet élève, ou cette élève, pour chaque unité d’enseignement auquel il est inscrit (ou elle est inscrite), sont stockées dans une instance de SuiviUE.
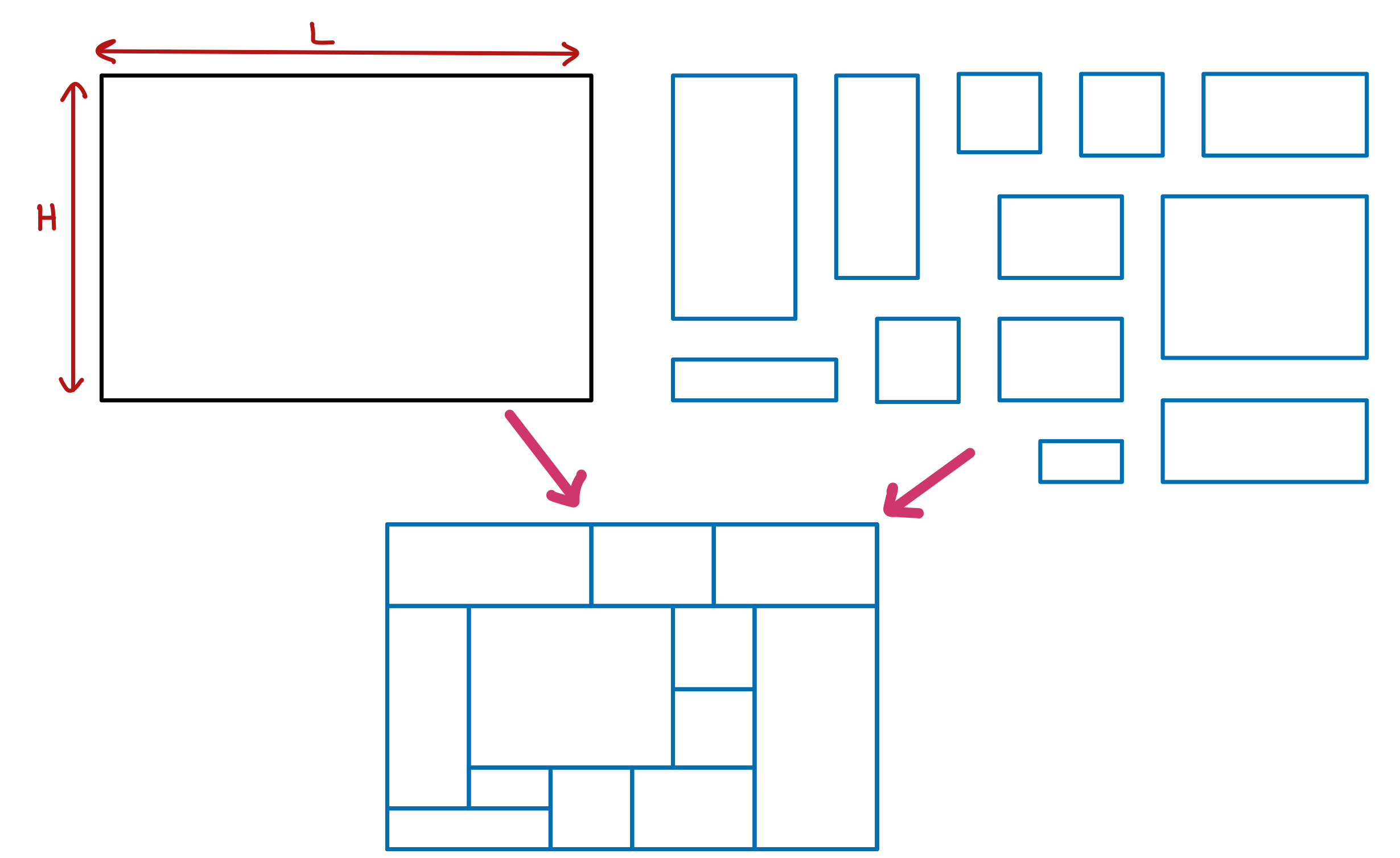
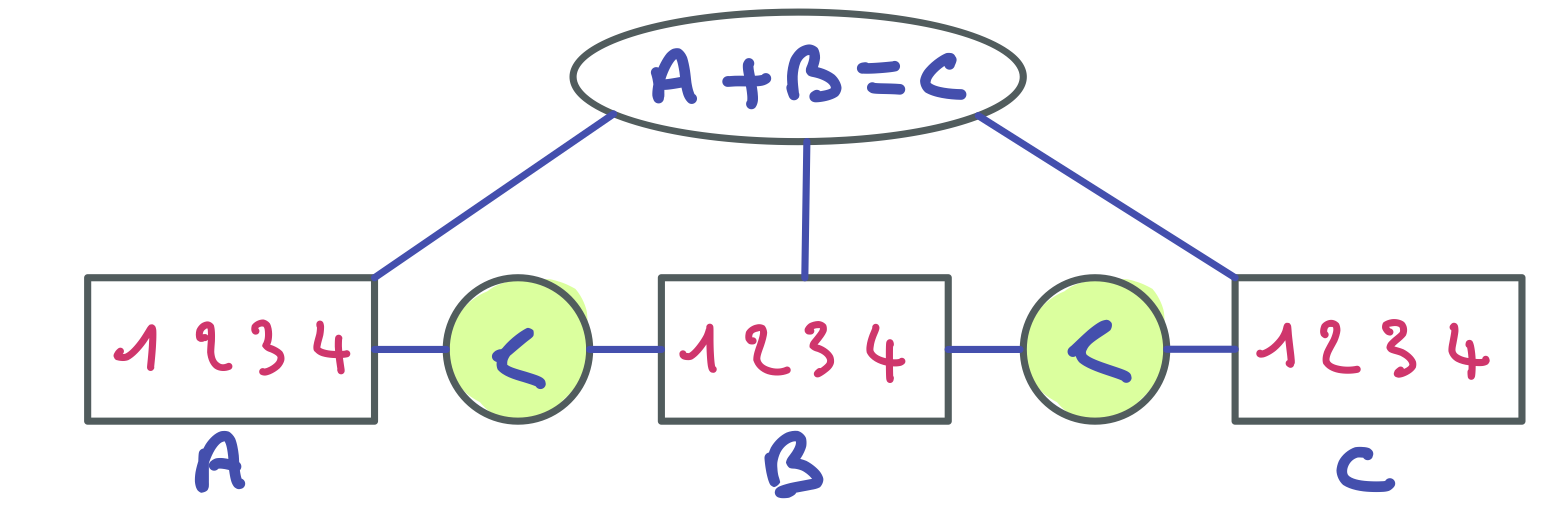
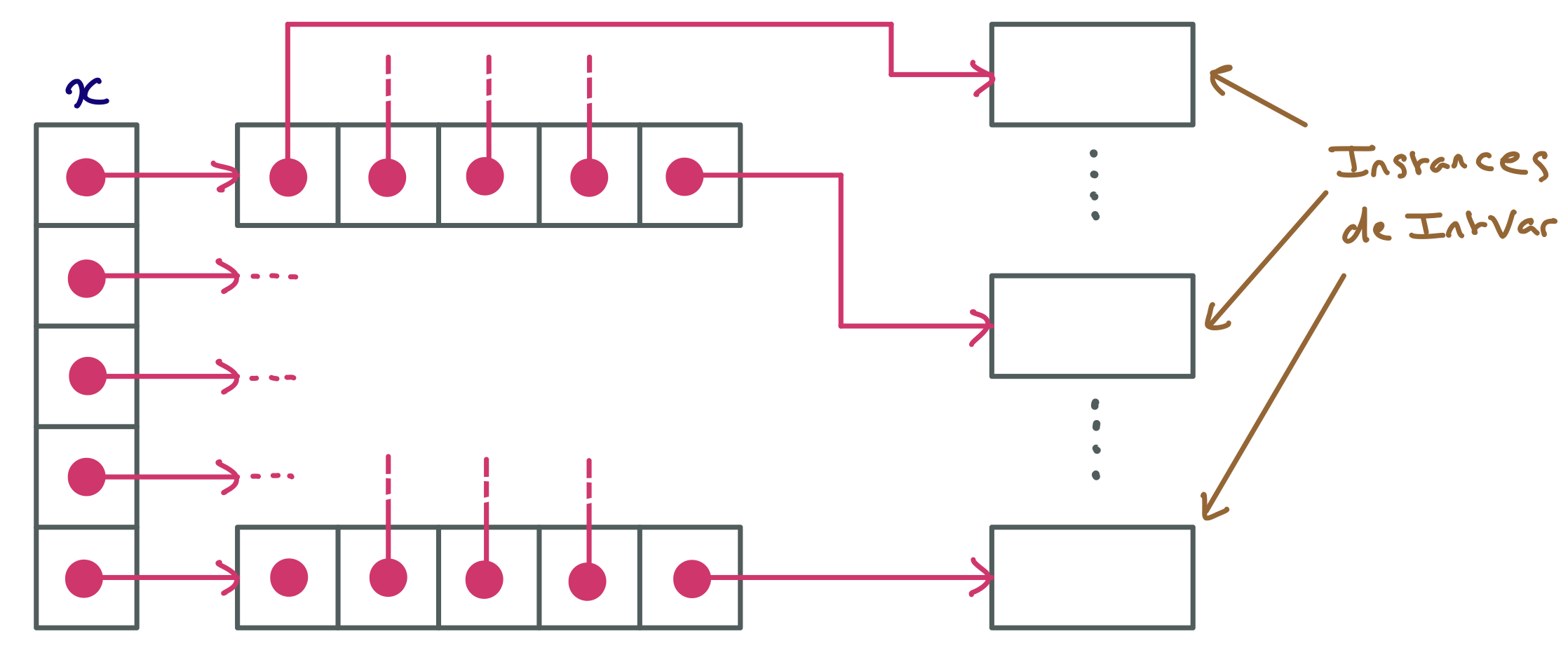
Nous avons là une structure de donnée un peu complexe qui peut être difficile à bien visualiser mentalement en lisant la description ce-dessus. Pour mieux visualiser les données représentées et leur organisation, voici une représentation graphique qui correspond à un exemple dans lequel :
- Il y a une instance de
SuiviEtu représentant un élève identifié par le numéro 1233, qui est inscrit à deux unités d’enseignement : Java et BD.
- Pour chacune de ces deux unités d’enseignement (UE en abrégé), il y a une instance de
SuiviUE qui contient l’intitulé de l’UE concernée, son coefficient, et les notes de l’élève 1233 pour cette UE.
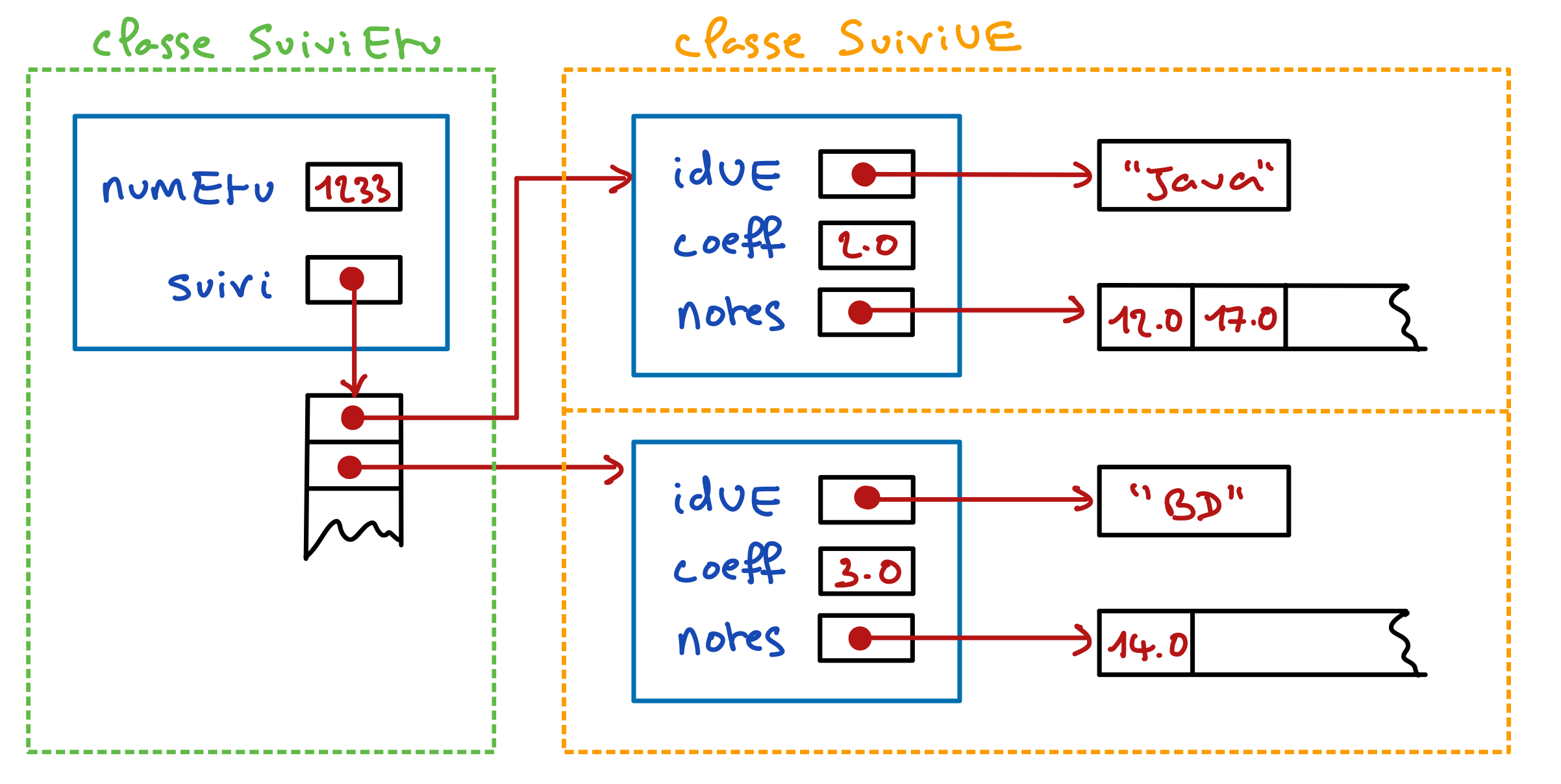
Avant d’écrire le code de la classe SuiviUE, nous allons voir comment elle devra être utilisée pour créer les données représentées ci-dessus, mais, dans un premier temps, sans nous soucier de la gestion des exceptions.
public class Main
{
public static void main(String[] args)
{// Attention, les exceptions ne sont pas gérées
SuiviEtu fiche = new SuiviEleve(1233);
fiche.addUE("Java", 2.0);
fiche.addUE("BD", 3.0);
fiche.addNote("Java", 12.0);
fiche.addNote("Java", 17.0);
fiche.addNote("BD", 14.0);
System.out.println(fiche.moyenne());
}
}
Appelons élève courant la personne apprenante désignée par le numéro passé en paramètre au constructeur de la classe SuiviEtu On voit que la classe SuiviEtu devra disposer d’un constructeur, d’une méthode addUE pour ajouter une unité d’enseignement au suivi de l’élève courant, d’une méthode addNote pour ajouter une note de l’élève dans une des UE auxquelles l’élève courant est inscrit, et une méthode moyenne permettant de calculer la moyenne général de l’élève courant.
Examinons à présent le détail du code de la classe SuiviEtu en considérant différentes situation pouvant produire des exceptions (il nous faudra donc les gérer dans la version définitive de notre fonction main donnée en exemple ci dessus). Procédons par étape. Voici une première partie de la classe SuiviEtu dans laquelle il n’y a ni levée, ni gestion d’exception.
public class SuiviEtu
{
private int numEtu;
private ArrayList<SuiviUE> suivi;
public SuiviEtu(int num)
{
this.numEtu = num;
this.suivi = new ArrayList<>();
}
public void addUE(String idUE, double coeff)
{
suivi.add(new SuiviUE(idUE, coeff));
}
// À compléter
}
Vérifiez que vous comprenez bien ce code. Le constructeur est assez classique. La méthode addUE permet d’ajouter une UE à laquelle l’élève courant est inscrit. Pour se faire, elle crée une instance de SuiviUE et elle l’ajoute à la liste des UE suivies par l’élève courant, qui est désignée par l’attribut suivi. N’allez pas trop vite. Si vous ne comprenez pas de manière limpide, revenez en arrière et regardez l’illustration basée sur l’exemple présenté plus haut.
À présent regardons le code de la méthode moyenne permettant de calculer la moyenne générale de l’élève courant.
public double moyenne() throws Defaillance // ligne A
{
double sum = 0.0; double sumCoeffs = 0.0;
for(SuiviUE sue : suivi)
{
sum += sue.moyenne() * sue.coeff;
sumCoeffs += sue.coeff;
}
return sum / sumCoeffs;
}
Il y a une nouveauté. Cette méthode appelle la méthode moyenne de la classe suiviUE, qui est susceptible de produire une exception de type Defaillance. Mais au lieu d’intercepter cette exception avec un try … catch, elle la fait remonter en indiquant throws Defaillance (ligne A). Ceci signifie que c’est la méthode qui appelle la méthode moyenne de la classe SuiviEtu qui va devoir soit gérer cette exception, soit la faire remonter.
Mais tout ceci ne nous sert à rien tant qu’on ne peut pas attribuer de note à l’élève courant, ce qui est le rôle de la méthode addNote de la classe SuiviEtu Cette méthode devra rechercher dans la liste des UE auxquelles est inscrit l’élève courant (désignée par l’attribut suivi) l’instance de SuiviUE dans laquelle il faut placer la note à ajouter. Cette recherche est basée sur l’intitulé de l’UE concernée. Mais que faire si l’UE en question n’est pas dans la liste ? C’est à dire par exemple si on veut ajouter une note à l’UE "Allemand" mais que cette UE n’a pas été ajoutée à celle suivies par l’élève courant avec la méthode addUE ?
On va lever une exception ! Mais pour éviter de tout mélanger, on va introduire pour cet usage un nouveau type d’exception appelé BadUE.
public class BadUE extends Exception
{
private String idUE;
public BadUE(String id)
{
this.idUE = id;
}
public String getId()
{
return idUE;
}
}
Voilà, maintenant voici le code de la méthode addNote de la classe SuiviEtu.
public void addNote(String idUE, double note) throws BadUE
{
for(SuiviUE sue : suivi)
{
if(sue.idUE.equals(idUE))
{
sue.add(note); return;
}
}
throw new BadUE(idUE);
}
Le principe est assez simple : on parcours la liste des instances de SuiviUE enregistrées dans la liste désignée par l’attribut suivi jusqu’à trouver celle ayant l’intitulé recherché. Si on la trouve, alors on utilise la méthode add de la classe SuiviUE pour ajouter la note, puis on arrête l’exécution de la méthode avec return. Si on ne la trouve pas, on lève une exception de type BadUE.
Si vous êtes débutant ou débutante, vous devez faire attention à ne pas confondre l’identifiant (ou nom ou intitulé) d’une unité d’enseignement et l’instance de SuiviUE représentant les notes obtenue par un élève dans cette UE.
Bien que le principe soit simple, il y a une subtilité qui, si elle n’est pas maîtrisée, pourra vous amener à faire des erreurs lorsque vous aurez besoin de comparer deux chaînes de caractères (représentant des identifiants d’UE).
Pour chaque instance sue de la la classe SuiviUE stockée dans la liste désignée par l’attribut suivi de l’instance courante de la classe SuiviEtu…
for(SuiviUE sue : suivi)
…on veut comparer l’intitulé de l’UE représentée par sue, c’est à dire sue.idUE, avec l’intitulé de l’UE à rechercher, c’est à dire idUE, passé en paramètre. On veut donc comparer les deux chaînes de caractères désignées respectivement par idUE et sue.idUE. Pour comparer ces chaînes, on pourrait être tenter d’écrire…
if(sue.idUE == idUE) // ERREUR !
…, ce qui serait une mauvaise idée. En effet, les chaînes sont des objets, des instances de String, désignées par leur référence, c’est à dire leurs adresses en mémoire. L’opérateur == compare les références et non les contenus des chaînes. Pour comparer les contenus, on peut utiliser la méthode equals qui a été définie dans le classe pédéfinie String pour cet usage. D’où la ligne…
if(sue.idUE.equals(idUE))
Il nous reste à revoir notre méthode main car telle qu’elle est codée plus haut, elle ne gère pas les deux types d’exceptions qu’elle peut recevoir : Defaillance et BadUE. Voici une manière de procéder.
public class Main
{
public static void main(String[] args)
{
SuiviEtu fiche = new SuiviEtu(1233);
fiche.addUE("Java", 2.0);
fiche.addUE("BD", 3.0);
try
{
fiche.addNote("Java", 12.0);
fiche.addNote("Java", 17.0);
fiche.addNote("BD", 14.0);
System.out.println(fiche.moyenne());
}
catch(Defaillance ue)
{// Traitement des exceptions produites par fiche.moyenne()
System.out.println("Défaillance à l'UE : " + ue.getID());
}
catch(BadUE ue)
{// Traitement des exceptions produites par fiche.addNote(...)
System.out.println("UE non référencée : " + ue.getId());
}
}
}
Examinez ce code avec attention. La création de la fiche de suivi de l’élève 1233 et l’ajout des deux UE auxquelles cet élève est inscrit reste identique puisque ni le constructeur, ni la méthode addUE de la classe SuiviEtu ne sont susceptibles de lever une exception.
Par contre, les lignes qui suivent ont été placées dans un try … catch chargé d’intercepter, si applicable, les deux types d’exception pouvant être produites.
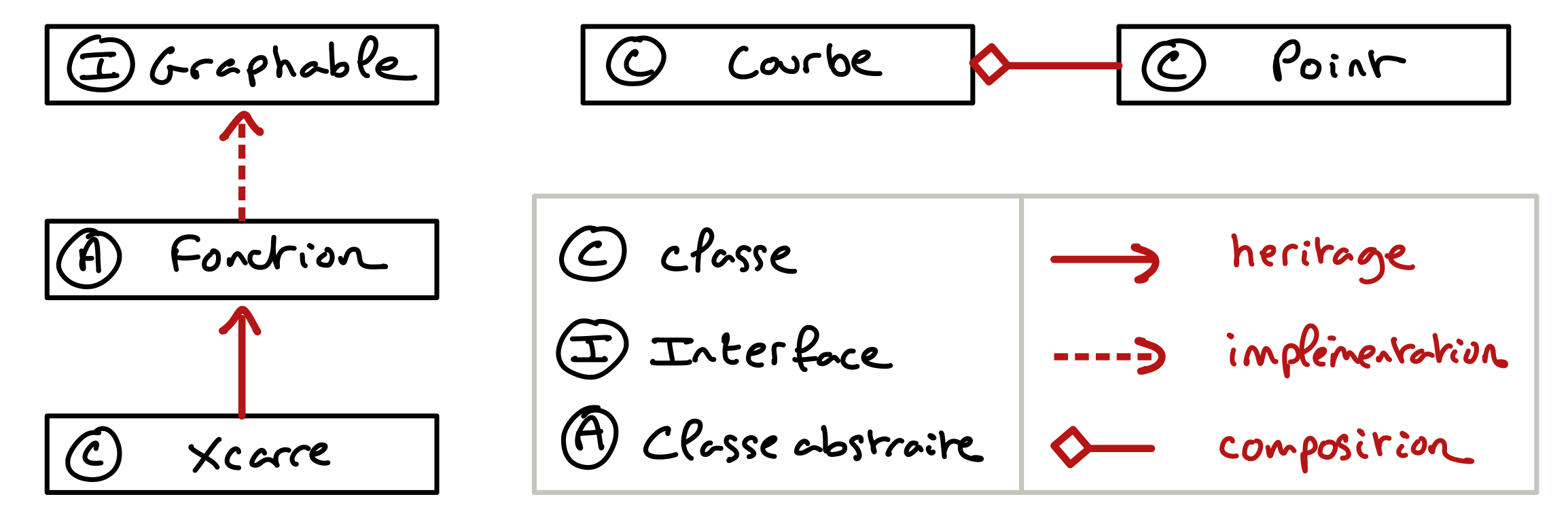
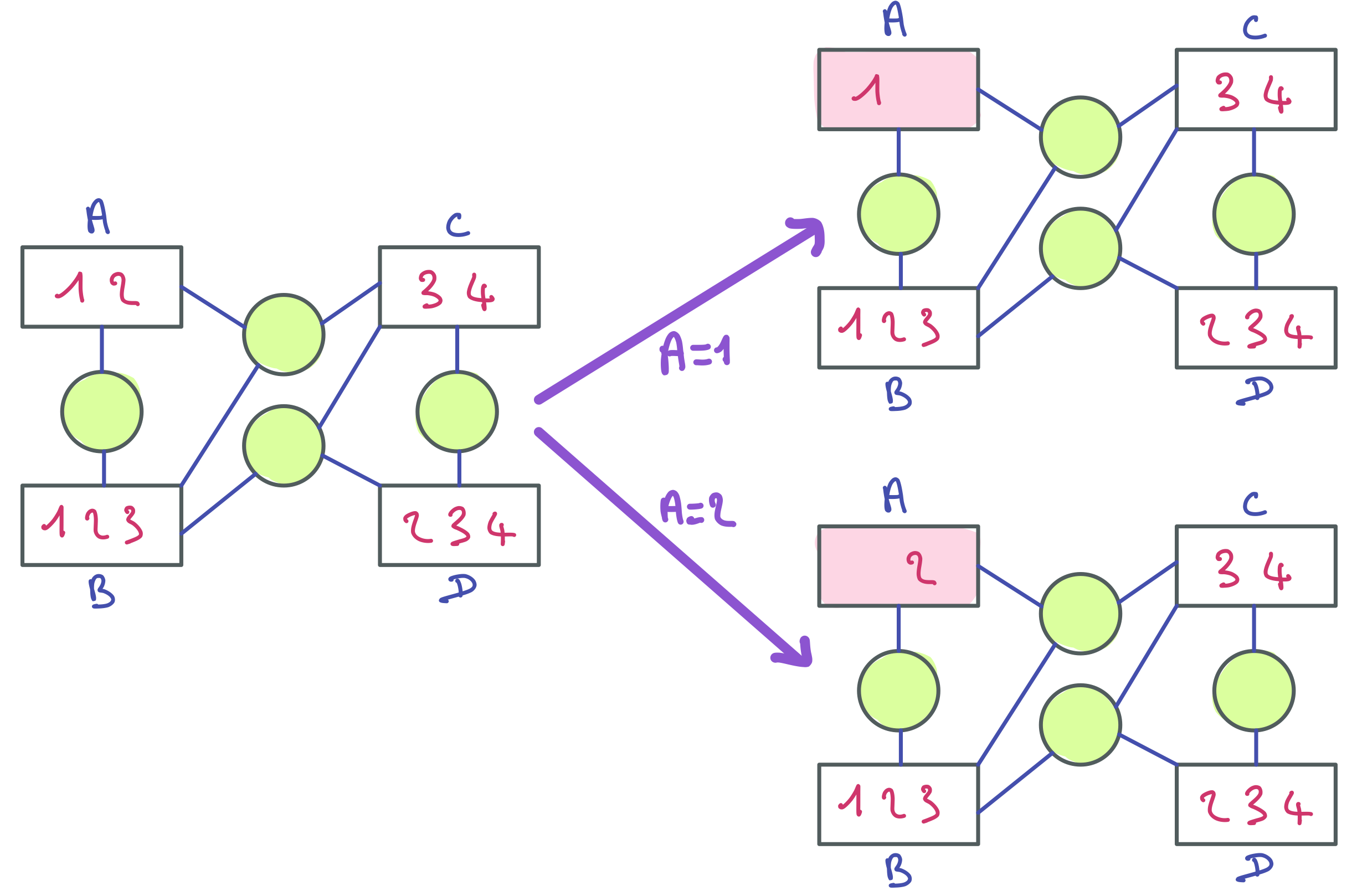
Ce programme est un peu compliqué lorsqu’on l’examine morceau par morceau sans avoir une vue d’ensemble. Certaines personnes peuvent avoir cette vue d’ensemble juste en lisant les codes des classes, mais si vous êtes débutante ou débutant, cela peut être très difficile. Ce schéma devrait vous aider. Il présente chacune des deux classes, leurs attributs, constructeurs et principales méthodes, et fait apparaitre le graphe d’appel qui matérialise par une flèche les appels de méthodes.
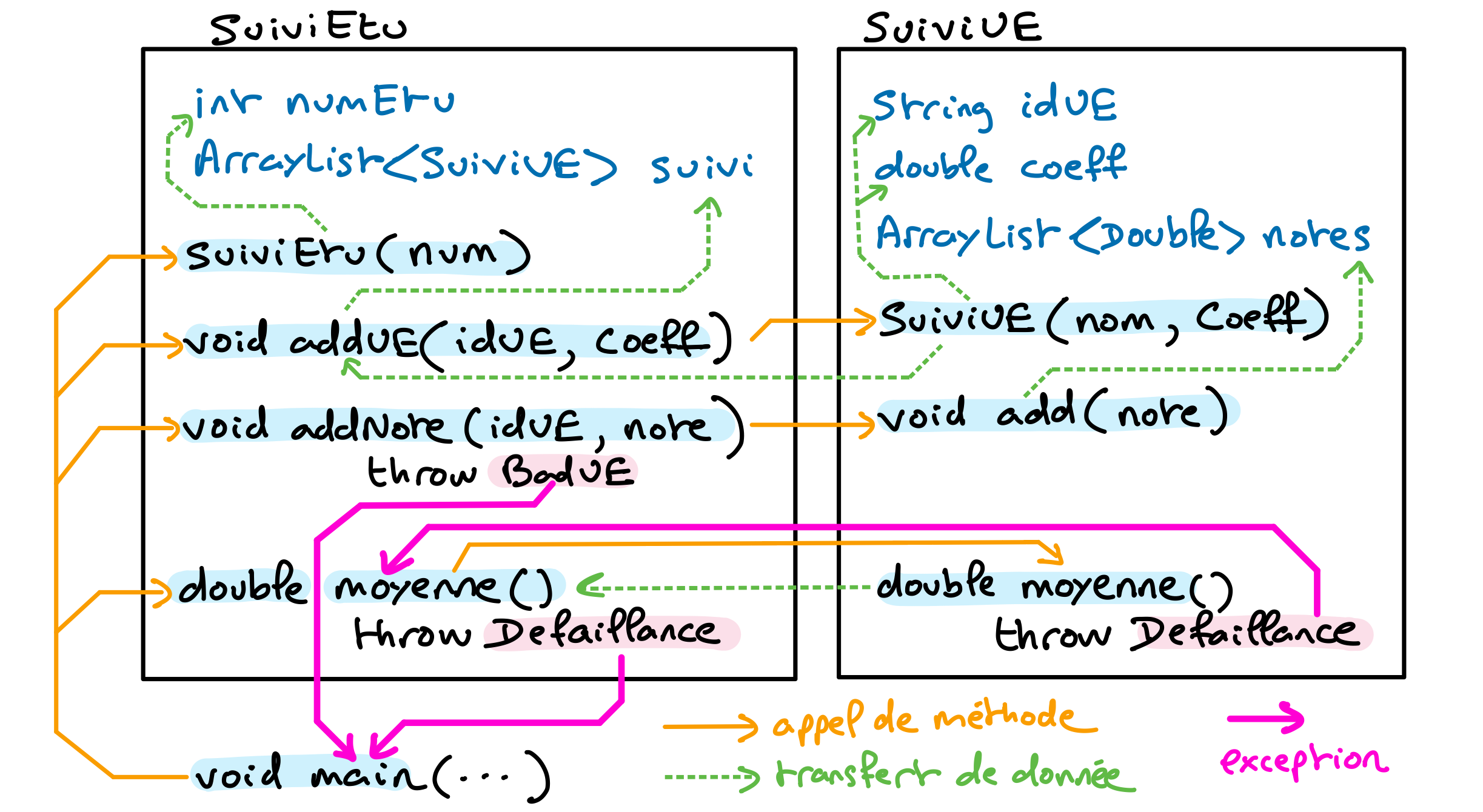
Par exemple, la méthode main appelle la méthode moyenne de la classe SuiviEtu qui appelle la méthode moyenne de la classe SuiviUE. On voit que la méthode moyenne de SuiviUE peut lever une exception de type Defaillance, qui est récupérée pat la méthode moyenne de la classe SuiviEtu qui la remonte à la méthode main.
Exercices de découverte
D-dec-20
Lors de l’exécution de la méthode main ci dessus, aucune exception n’est levée. Faite une modification pour qu’une exception de type Defaillance soit levée et dites quels seront alors les affichages réalisés lors de l’exécution.
"Solution"
Dans le bloc try on met en commentaire la ligne qui ajoute une note pour l’UE "BD".
try
{
fiche.addNote("Java", 12.0);
fiche.addNote("Java", 17.0);
//fiche.addNote("BD", 14.0);
System.out.println(fiche.moyenne());
}
À l’exécution, le programme affiche uniquement :
Défaillance à l'UE : BD
D-dec-21
En repartant de la méthode main donnée plus haut, celle qui ne produit aucune exception, faire une modification pour qu’une exception de type BadUE soit levée et dites quels seront alors les affichages réalisés lors de l’exécution.
"Solution"
Par exemple on peut remplacer "BD" par "GEO" dans la troisième ligne du bloc try.
try
{
fiche.addNote("Java", 12.0);
fiche.addNote("Java", 17.0);
fiche.addNote("GEO", 14.0);
System.out.println(fiche.moyenne());
}
À l’exécution, le programme affiche uniquement :
UE non référencée : GEO
D-dec-22
Dans la version de la classe SuiviEtu donnée plus haut, la méthode moyenne, si elle reçoit une exception de type Defaillance, la fait remonter. Modifiez la méthode de manière à ce que, si elle reçoit une exception de type Defaillance, elle affiche le message "L’élève n’a pas de note dans l’UE {ID de l’ue}" et retourne 0.0.
"Solution"
public double moyenne_bis()
{
double sum = 0.0; double sumCoeffs = 0.0;
for(SuiviUE sue : suivi)
{
try
{
sum += sue.moyenne() * sue.coeff;
}
catch(Defaillance d)
{
System.out.println("L'élève n'a pas de note dans l'UE " + d.getID());
return 0.0;
}
sumCoeffs += sue.coeff;
}
return sum / sumCoeffs;
}
D3 : Compléments
Le bloc Finaly
Un try … catch peut être suivi d’un bloc finally. Le code situé dans ce bloc est systématiquement exécuté à l’issue du try … catch qu’i y ait eu ou non interception d’exception, et même si un return est réalisé dans un bloc catch.
Un usage typique est de refermer un fichier ayant été ouvert dans le bloc try, mais cela sort du périmètre de cet enseignement.
Les exceptions "run time"
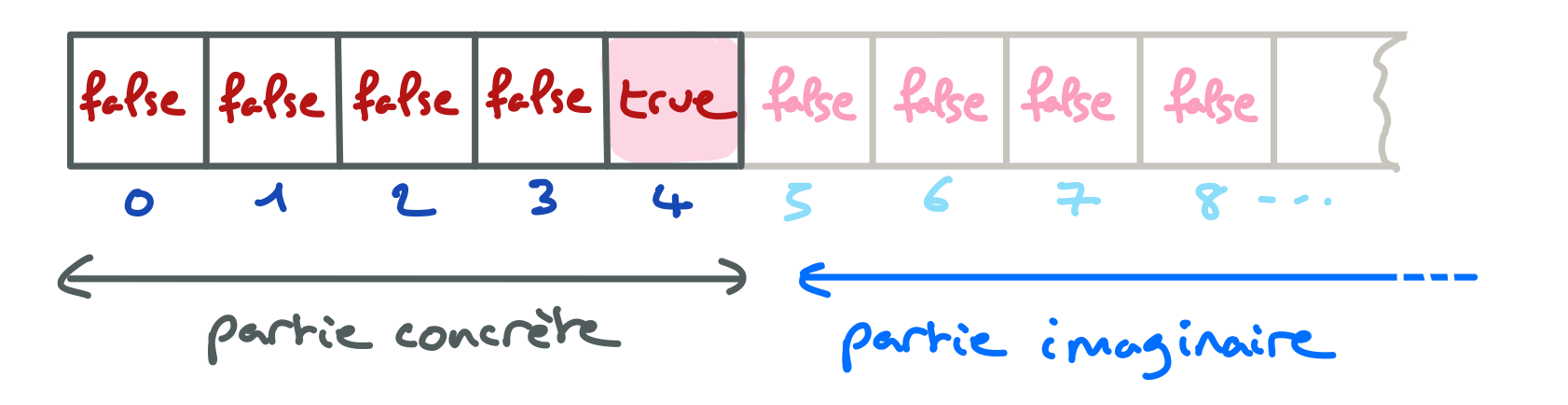
Les exceptions dérivant de la classe RuntimeException ont la particularité de remonter automatiquement, si elle ne sont pas interceptées, sans que les méthodes où elles se produisent aient à le spécifier avec throws. L’usage typique est la gestion des erreurs de programmations qui doivent entrainer un arrêt de l’exécution du programme. Java produit lui même de telles exceptions, par exemple lors d’une tentative d’appel d’une méthode avec une variables contenant une valeur null au lieu de la référence d’un objet (NullPointerException), ou encore lors d’une tentative d’accès à une cellule de tableau à un indice incorrect (OutOfBoundException).
Vous pouvez créer et intercepter des exceptions de type RuntimeException, et vous pouvez également intercepter celles produites par Java. Les exceptions de ce type non interceptées remontent jusqu’à la machine virtuelle Java, provoquant l’affichage d’un message d’erreur indiquant dans quelle méthode le problème est survenu.
Faisons l’expérience suivante.
public class TestRuntimeExceptions
{
public static void main(String[] args)
{
int[] tab = new int[5];
tab[5] = 12;
System.out.println("Exécution terminée");
}
}
À l’exécution, le programme s’arrête et affiche :
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException:
Index 5 out of bounds for length 5 at TestRuntimeExceptions.main(TestRuntimeExceptions.java:8)
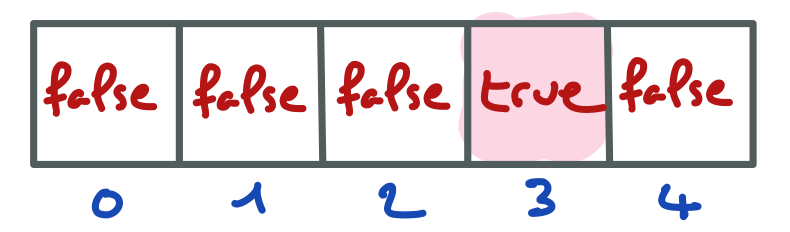
On voit que le message "Exécution terminée" ne s’est pas affiché car le programme a été interrompu avant par une exception de type ArrayIndexOutOfBoundsException déclenchée par une tentative d’accès à tab[5] alors que le tableau désigné par tab possède 5 cellules allant de tab[0] à tab[4]. (Une erreur classique de débutant.)
Voici un exemple d’interception de toute exception de type RuntimeException.
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12;
System.out.println("Exécution terminée");
}
catch(RuntimeException e)
{
System.out.println("Une erreur s'est produite.");
}
}
Lors de l’exécution, on obtient l’affichage :
Une erreur s'est produite.
Le genre de message un peu énervant parce que pas très informatif…
Si on écrit ceci…
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12;
System.out.println("Exécution terminée");
}
catch(RuntimeException e)
{
System.out.println(e);
}
}
…alors on obtient l’affichage :
ArrayIndexOutOfBoundsException: Index 5 out of bounds for length 5
L’affichage de l’instance d’exception e a invoqué la méthode toString de la classe ArrayOutOfBoundsException qui a fourni des informations utiles.
Exercices de découverte
D-dec-30
Soit la méthode main suivante :
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12;
System.out.println("Exécution terminée");
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
throw e;
}
}
Tentez de prévoir ce que le l’exécution de cette méthode va afficher à l’écran.
"Solution"
Comme une exception de type Runtime Exception est produite dans le bloc try, le bloc catch sera exécuté et affichera "----- ERREUR D'EXECUTION -----". Le code situé dans le bloc try après la ligne où l’erreur se produit ne sera pas exécuté.
Mais dans le bloc catch, l’exception est relancée par throw e ! (Celle là, on ne vous l’avait encore jamais faite.) Donc cette exécution est remontée à la machine virtuelle et provoque un affichage détaillé de l’erreur à l’origine de l’exception. On obtient l’affichage :
----- ERREUR D'EXECUTION -----
Exception in thread "main" ArrayIndexOutOfBoundsException:
Index 5 out of bounds for length 5 at TestRuntimeExceptions.main(TestRuntimeExceptions.java:10)
D-dec-31
Soit la méthode main suivante :
public class TestRuntimeExceptions
{
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12;
System.out.println("Exécution terminée");
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
}
}
}
On voudrait que le message "Exécution terminée" s’affiche toujours à l’issue de l’exécution du programme, qu’il y ait ou non une exception produite dans le bloc catch. Avec la nouvelle version, si on écrit tab[5] = 12 dans le bloc try, on devra avoir l’affichage…
----- ERREUR D'EXECUTION -----
Exécution terminée
…alors que si on écrit tab[4] = 12 on aura l’affichage :
Exécution terminée
Essayez de trouver deux manières d’obtenir ce résultat, une utilisant un bloc finally et une autre solution sans utiliser un tel bloc.
"Solution"
Avec un bloc finally, on peut écrire :
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12;
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
}
finally
{
System.out.println("Exécution terminée");
}
}
Sans utiliser un tel bloc, on peut écrire :
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[4] = 12;
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
}
System.out.println("Exécution terminée");
}
En effet, s’il n’y a pas de return ou de levée d’une exception ou autre instruction qui arrête le programme dans le bloc catch, l’exécution reprend son cours après les blocs try … catch et le bloc finally n’est pas vraiment utile. En revanche, si un bloc catch interrompt le programme, le bloc finally sera quand même exécuté alors que le code qui est au delà ne le sera jamais.
D-dec-32
Soit la méthode main suivante :
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12; // ligne A
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
return;
}
System.out.println("Exécution terminée");
}
Qu’affiche très exactement l’exécution du programme ? Même question si on supprime la ligne A ou si on la met complètement en commentaire ?
"Solution"
Avec la ligne A :
----- ERREUR D'EXECUTION -----
Sans la ligne A :
Exécution terminée
D-dec-33
Soit la méthode main suivante :
public static void main(String[] args)
{
try
{
int[] tab = new int[5];
tab[5] = 12; // ligne A
}
catch(RuntimeException e)
{
System.out.println("----- ERREUR D'EXECUTION -----");
return;
}
finally
{
System.out.println("Exécution terminée");
}
}
Qu’affiche très exactement l’exécution du programme ? Même question si on supprime la ligne A ou si on la met complètement en commentaire ?
"Solution"
Avec la ligne A :
----- ERREUR D'EXECUTION -----
Exécution terminée
Sans la ligne A :
Exécution terminée
Exercices d’assimilation
D-ass-00
La méthode suivante permet de saisir un entier au clavier.
public static int lireInt()
{
return new Scanner(System.in).nextInt();
}
Mais si la valeur saisie n’est pas un entier, elle produit une exception de type InputMismatchException. Proposez une nouvelle version de la méthode lireInt qui en cas de saisie correcte, retourne une instance de la classe enveloppe Integer contenant l’entier saisi, et qui dans le cas contraire retourne null.
"Indice
Voici un squelette de la méthode à compléter. L’exception attendue dans la partie catch est de type InputMismatchException, mais le type Exception plus général convient aussi dans ce cas.
public static Integer lireInt()
{
try
{
// À compléter
}
catch(Exception e)
{
// À compléter
}
}
"Solution"
Voici une solution complète. Des variantes sont possibles. Au besoin faites des essais sur machine.
public static Integer lireInt()
{
try
{
return new Scanner(System.in).nextInt();
}
catch(Exception e)
{
return null;
}
}
D-ass-01
Proposez une troisième version de la méthode lireInt de l’exercice précédent qui en cas de saisie correcte, retourne l’entier saisi (la valeur de retour est donc de type int, comme pour la première version), et qui, en cas de saisie incorrecte, redemande à l’utilisateur de faire une nouvelle saisie jusqu’à ce qu’une saisie correcte soit réalisée.
"Indice
Voici un squelette d’une solution simple. La présence du while(true) pout choquer certains puristes, mais elle ne me semble pas nuire à la lisibilité du code. La sortie de la boucle se fait par l’instruction return lorsque le « job » de la méthode est terminé, c’est-à-dire quand l’utilisateur a réalisé une saisie correcte.
public static Integer lireInt()
{
while(true)
{
try
{
// À compléter
}
catch(Exception e)
{
// À compléter
}
}
}
"Solution"
public static Integer lireInt()
{
while(true)
{
try
{
return new Scanner(System.in).nextInt();
}
catch(Exception e)
{
System.out.println("Saisie incorrecte, veuillez recommencer");
}
}
}
D-ass-02
Modifiez le constructeur de la classe Date du badge B pour qu’il lève une exception de type BadDate, à définir, si la valeur du jour ou du mois est incorrecte ou si celle de l’année est inférieure à MINY ou supérieure MAXY, deux constantes de classe définies dans BadDate. La classe BadDate dispose d’un constructeur acceptant un paramètre de type String qui appelle le constructeur Exception(String message). C’est ce constructeur qui devra être utilisé pour lever (si applicable) l’exception en lui passant en argument un message indiquant la nature du problème (Année incorrecte, ou Jour incorrect ou Mois incorrect). Un jour est considéré comme incorrect s’il est inférieur à 1 ou supérieur à 31. On ne prend pas en compte la durée réelle des mois dans cette version simplifiée. Réalisez une méthode de test qui tente de créer une date incorrecte, intercepte l’exception et affiche un message d’erreur pertinent.
"Indice
Commençons par définir la classe d’exception.
public class BadDate extends Exception
{
public BadDate(String message)
{
super(message);
}
}
"Indice
Regardons les modifications à faire dans la classe Date. Voici la déclaration des constantes (initialisées avec des valeurs arbitraires à titre d’exemple) et le squelette du constructeur à modifier.
public class Date
{
final public static int MAXY = 2100;
final public static int MINY = 1700;
private int jour;
private int mois;
private int annee;
public Date(int jour, int mois, int annee) throws BadDate
{
// À compléter
this.jour=jour; this.mois=mois; this.annee=annee;
}
}
"Indice
Voici le détail du constructeur de la classe Date, qui lève une même exception, mais avec des messages d’erreur différents selon le paramètre erroné.
public Date(int jour, int mois, int annee) throws BadDate
{
if((annee<MINY)||(annee>MAXY))
{
throw new BadDate("Annee incorrecte");
}
else if ((jour<1)||(jour>31))
{
throw new BadDate("Jour incorrect");
}
else if ((mois<1)||(mois>12))
{
throw new BadDate("Mois incorrect");
}
this.jour=jour; this.mois=mois; this.annee=annee;
}
Il vous reste à écrire la méthode de test.
"Solution"
Voici le détail de la méthode de test.
public static void test()
{
try
{
Date d = new Date(32,7,2012);
}
catch(BadDate e)
{
System.out.println(e);
}
}