Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Implémentation avec CHOCO v4

Objectif

Être capable de concevoir une application Java permettant de résoudre un problème de satisfaction de contraintes en utilisant la bibliothèque CHOCO version 4.

Prérequis

Partie B et bases de programmation en JAVA.

Introduction

Entendons-nous bien. La programmation par contraintes est une programmation déclarative : on spécifie un problème à l’aide de contraintes, et un solveur résout ce problème. L’intérêt est précisément de ne pas avoir à programmer un solveur. Java n’est pas un langage déclaratif mais impératif, qui exige de détailler toutes les étapes et opérations nécessaires à l’exécution d’un programme.

Alors pourquoi et comment utiliser un langage impératif pour faire de la programmation déclarative ?

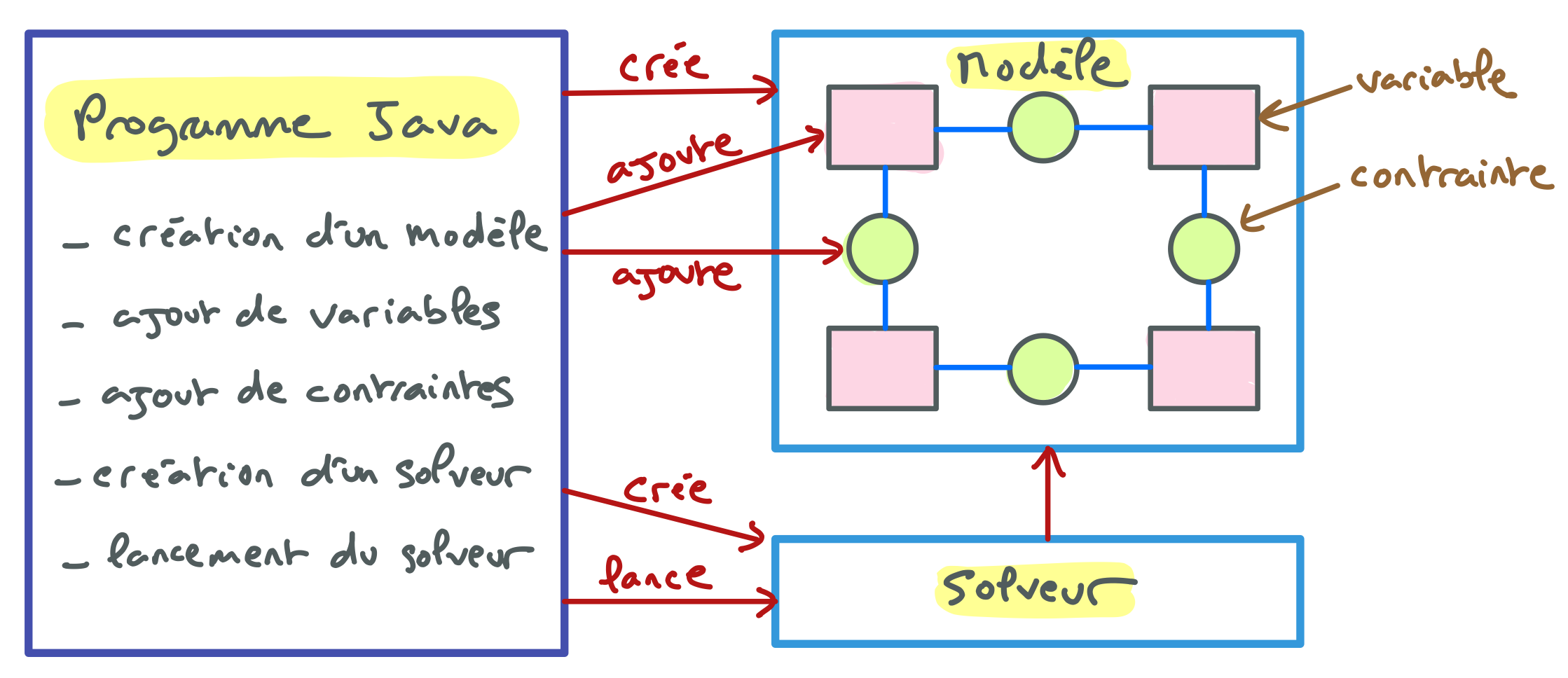
Il faut comprendre que les applications réalisées avec la bibliothèque CHOCO s’exécutent en deux temps. Dans un premier temps, un programme Java produits des objets de types variables et contraintes, qui sont placés dans un objet appelé modèle, qui représente un réseau de contraintes.

Une application utilisant CHOCO exécute un algorithme qui « fabrique » une spécification déclarative d’un problème de satisfaction de contraintes. Dans un deuxième temps, un objet solveur prend en charge le modèle préalablement construit pour résoudre le réseau de contraintes. Donc le code Java ne sert pas à résoudre le problème, mais à construire des réseaux de contraintes représentant des instances du problème à résoudre. La résolution en elle-même est assurée par le solveur fourni par CHOCO.

Avant d’aller plus loin, vous devez récupérer la bibliothèque CHOCO qui est disponible sous la forme d’une archive au format jar en suivant les instructions du site choco-solver.org. On vous envoie vers un dépôt github où, en cherchant bien, vous pourrez trouver un lien vers la "latest release". Au moment où j’écris ces lignes, il s’agit de la version 4.10.6. Vous arrivez enfin à une page proposant plusieurs archives. Celle qui nous intéresse est nommée choco-solver-4.10.6-jar-with-dependencies.jar au moment où j’écris ce ligne. Il se peut qu’il s’agisse d’une version ultérieur lorsque vous vous rendrez sur le site, mais l’important est que la bonne archive a l’extension jar et comporte les termes choco-solver et with-dependencies dans son nom.

Vous devez ensuite faire en sorte d’utiliser cette bibliothèque dans le code Java que vous allez écrire et compiler. Les IDE proposent tous un moyen spécifique de faire cela. Il faut parfois tâtonner un peu.

Exemple introductif

Avant de coder une application CHOCO, il faut modéliser le problème à résoudre sous la forme d’un réseau de contraintes comme nous avons appris à le faire dans la préparation du badge B.

Nous parlons ici du problème suivant : peut-on placer n reines sur un échiquier n par n de manière à qu’il y ait exactement une reine sur chaque ligne et chaque colonne et au plus une reine sur chaque diagonale ?

Pour modéliser ce problème, nous utilisons $n$ variables $v_{0},\ldots,\ v_{n – 1}$ à domaines ${ 1..n}$. Chaque variable est associée à une colonne de l’échiquier. Une assignation $v_{i} = j$ signifie que la reine située dans la colonne $i$ se trouve en ligne $j$.

La figure ci-dessous représente une solution pour $n = 5$ et l’assignation des variables $v_{0}$ à $v_{4}$ qui représente cette solution.

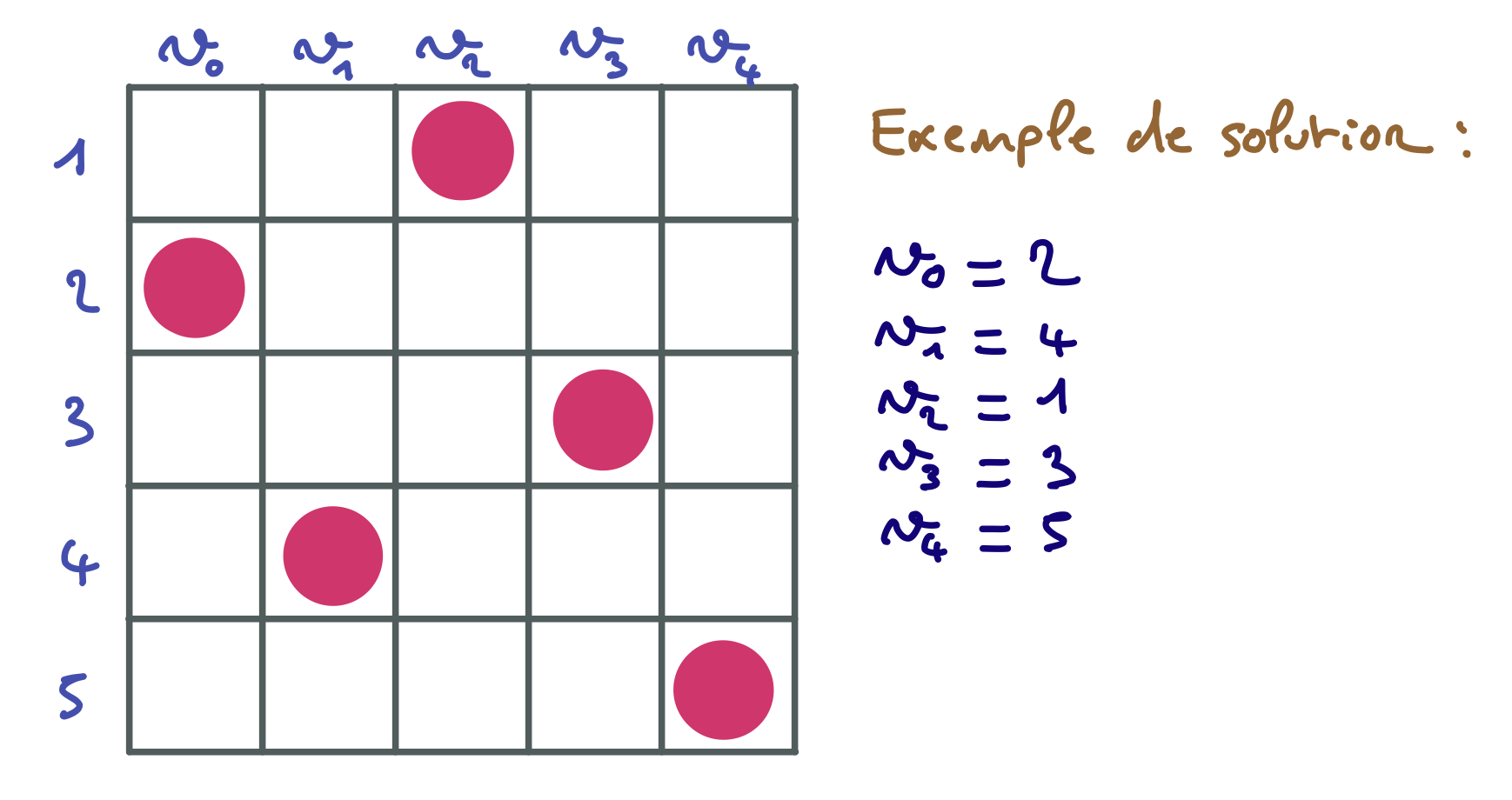
Pour chaque couple $(i,j),\ i \in 0..(n – 2),\ j \in (i + 1)..(n – 1)$, on pose les trois contraintes suivantes :

$v_{i} \neq v_{j}$, qui interdit que les reines des colonnes $i$ et $j$ soient une même ligne.
$v_{i} \neq v_{j} – (j – i)$, qui interdit que les reines des colonnes $i$ et $j$ soient sur une même diagonale descendante.
$v_{i} \neq v_{j} + (j – i)$, qui interdit que les reines des colonnes $i$ et $j$ soient sur une même diagonale montante.

Par exemple, on aura trois contraintes reliant les variables $v_{0}$ et $v_{2}$, à savoir $v_{0} \neq v_{2}$, $v_{0} \neq v_{2} – 2$ et $v_{0} \neq v_{2} + 2$. Si par exemple $v_{0} = 3$, ces trois contraintes interdiront les valeurs 2, 4 et 6 pour $v_{2}$.

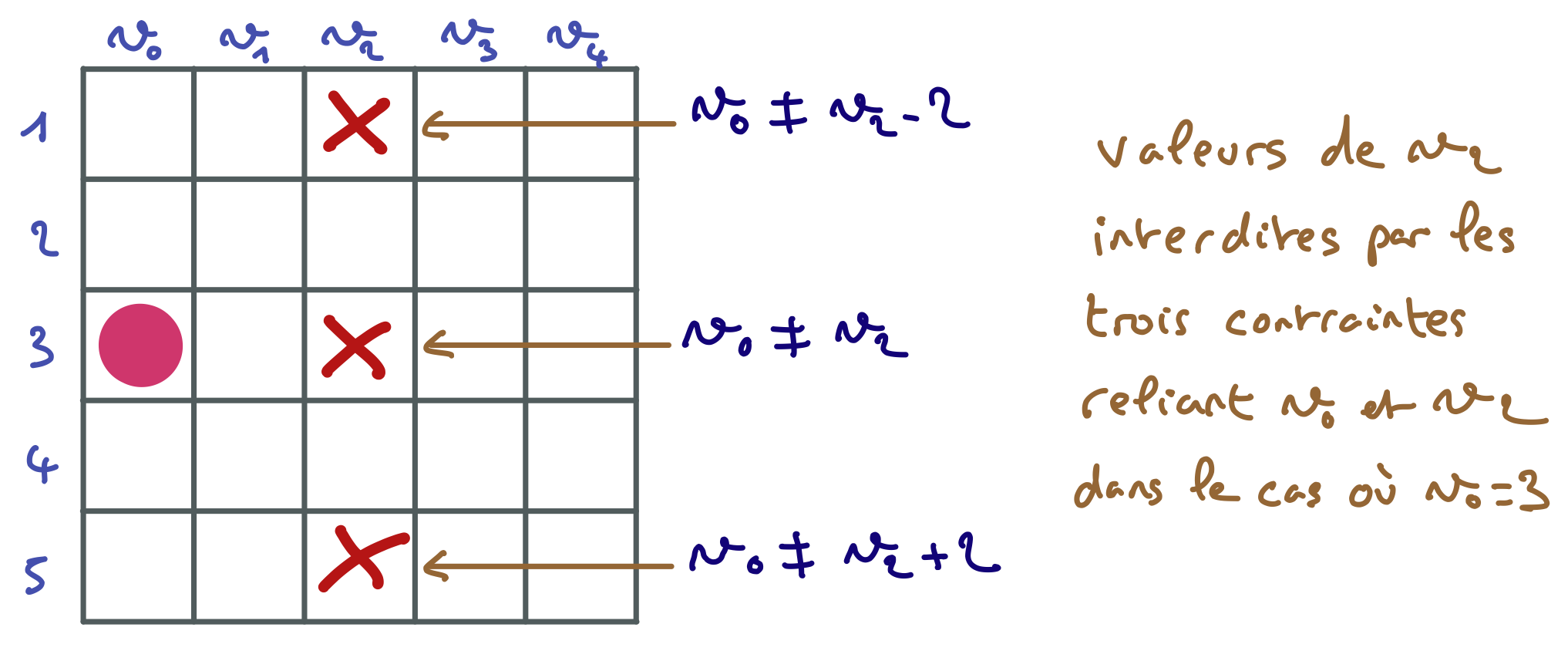
Au total, pour $n$ reines, on aura $3n(n – 1)/2$ contraintes.

Il nous faut maintenant traduire ce modèle en un ensemble d’objets créés avec la bibliothèque CHOCO. Voici les différentes étapes.

Création du modèle

Ces deux lignes permettent de créer un modèle (instance de la classe Model) à laquelle seront ensuite ajoutées les contraintes et les variables. La chaîne passée en paramètre est purement « cosmétique ».

    int n = 8;
    Model model = new Model(n + "-queens problem");

Création des variables

Ces lignes permettent de créer les variables du réseau de contraintes. Attention. Nous parlons bien ici des variables du réseau de contraintes, dont les domaines contiennent des entiers. Ces variables ne sont pas des variables de type int de Java. Ce sont des instances de la classe IntVar de CHOCO qui représentent les variables du réseau de contraintes sur lequel le solveur CHOCO va raisonner.

    IntVar[] vars = new IntVar[n];
    for(int q = 0; q < n; q++)
    {
        vars[q] = model.intVar("Q_"+q, 1, n);
    }

La première ligne crée un tableau qui regroupera toutes les variables du problème. Attention, cette liste produit juste un tableau dont les cellules contiennent la pseudo-référence null.

En Java, les cellules d’un tableau, tout comme les variables ayant un type non scalaire T ne contiennent jamais une instance de type T, mais contiennent soit la valeur null, soit la référence d’un objet de type T.

En résumé, une variable ou une cellule de tableau ne peut pas contenir un objet, mais seulement sa référence. Donc dans notre cas, la création du tableau ne crée pas les variables de notre réseau mais juste les cellules destinées à contenir les références de ces variables.

C’est la boucle for qui va créer les variables de notre réseau de contraintes, qui est appelé modèle dans la documentation CHOCO, et placer les références de ces variables, représentées par des objets de type IntVar, dans le tableau vars.

La création de chaque variable est assurée par la méthode intvar de la classe Model de CHOCO.

L’appel model.intVar(\"Q\_\"+q, 1, n) retourne la référence un objet de type IntVar qui représente une variable (au sens de la programmation par contrainte) nommée Q_q (où q désigne la colonne associée à la variable) et de domaine 1..n (où n est le nombre de reines). Le nom de la variable est un attribut purement cosmétique qui pourra servir pour des affichages et lors de la mise au point du programme.

Création des contraintes

Les contraintes de notre modèle sont des objets de type Constraint. Ces objets sont produits par la méthode arithm de la classe Model. Différentes variantes surchargées de cette méthode permettent de construire aisément des contraintes arithmétiques à partir de variables, d’opérateurs et de constantes comme le montrent les lignes de code suivantes qui créent les contraintes pour le problème de n reines et les intègrent dans le modèle.

    for(int i  = 0; i < n-1; i++)
    {
        for(int j = i + 1; j < n; j++)
        {
            model.arithm(vars[i], "!=",vars[j]).post();
            model.arithm(vars[i], "!=", vars[j], "-", j - i).post();
            model.arithm(vars[i], "!=", vars[j], "+", j - i).post();
        }
    }

Examinons par exemple la ligne model.arithm(vars\[i\], \"!=\", vars\[j\], \"-\", j - i).post(). Cette ligne appelle la méthode arithm qui, avec les paramètres qui lui sont transmis, crée un objet de type Constraint représentant la contrainte $v_{i} \neq v_{j} – (j – i)$. La méthode post de la classe Constraint est ensuite appelée pour intégrer cette contrainte dans le modèle dans lequel elle a été créée. Il faut bien comprendre que du point de vue de CHOCO, les valeurs des variables Java i et j sont des constantes qui vont être figées dans la contrainte au moment de sa création.

En pratique, toutes les contraintes créées dans un modèle doivent y être intégrées par la méthode post sauf les contraintes dites réifiées.

La réification d’une contrainte $q$ sur un ensemble $V$ de variables est une contrainte $q^{r}$ sur $V \cup { r}$, où $r$ est une variable additionnelle appelée variable de réification à domaine Booléen {0,1}, telle que pour toute assignation $A$ sur $V$, $A \cup { r = 1}$ satisfait $q^{r}$ si et seulement si $A$ satisfait $q$ et $A \cup { r = 0}$ satisfait $q^{r}$ si et seulement si $A$ falsifie $q$. En résumé, la réification $q^{r}$ d’une contrainte $q$ peut toujours être satisfaite mais avec une valeur de sa variable de réification qui indique si $q$ est satisfaite par les valeurs des autres variables.

Si cela vous parait confus, pour l’instant retenez juste que pour ajouter des contraintes ordinaires, telle que celles que nous avons vu dans la préparation des parties A et B, il faut toujours intégrer les contraintes avec la méthode post et que si vous oubliez de le faire, le solveur ne prendra pas en compte les contraintes concernées.

Dans notre exemple, les boucles for imbriquées ne servent donc en aucun cas à résoudre le problème des n reines. Elles servent à fabriquer les contraintes qui spécifient ce problème et à intégrer ces contraintes dans le modèle qui servira ensuite au solveur pour résoudre le problème.

Résolution

Pour résoudre notre problème, il suffit de créer un objet de type Solveur et d’exécuter une méthode de cet objet permettant de lancer la résolution du réseau de contraintes spécifiée par le modèle précédemment construit. C’est ce que font les lignes de code ci-dessous.

    Solution solution = model.getSolver().findSolution();
    if(solution != null)
    {
        System.out.println(solution.toString());
    }

La méthode getSolver crée un objet de type Solver dédié au modèle représenté par l’objet model. La méthode findSolution appelée avec cet objet recherche une solution de ce modèle. Si le réseau de contraintes représenté par le modèle est incohérent, findSolution retourne null, sinon elle retourne un objet de type Solution qui contient les détails de la solution trouvée. La méthode toString de l’objet solution permet d’afficher les valeurs assignées aux variables par cette solution.

Il existe d’autres méthodes applicables aux objets de type Solver pour rechercher toutes les solutions du problème.

Voici le code complet de cet exemple introductif avec les imports des packages de CHOCO requis pour son fonctionnement.

public static void main(String[] args)
{
    int n = 8;
    Model model = new Model(n + "-queens problem");
    IntVar[] vars = new IntVar[n];
    for(int q = 0; q < n; q++)
    {
        vars[q] = model.intVar("Q_"+q, 1, n);
    }
    for(int i  = 0; i < n-1; i++)
    {
        for(int j = i + 1; j < n; j++)
        {
            model.arithm(vars[i], "!=",vars[j]).post();
            model.arithm(vars[i], "!=", vars[j], "-", j - i).post();
            model.arithm(vars[i], "!=", vars[j], "+", j - i).post();
        }
    }
    Solution solution = model.getSolver().findSolution();
    if(solution != null)
    {
        System.out.println(solution.toString());
    }
}

L’auteur a compilé ce code dans l’IDE IntelliJIDEA et l’exécution a produit l’affichage suivant :

Solution: Q_0=7, Q_1=4, Q_2=2, Q_3=5, Q_4=8, Q_5=1, Q_6=3, Q_7=6

Voici une représentation graphique de la solution trouvée par le solveur.

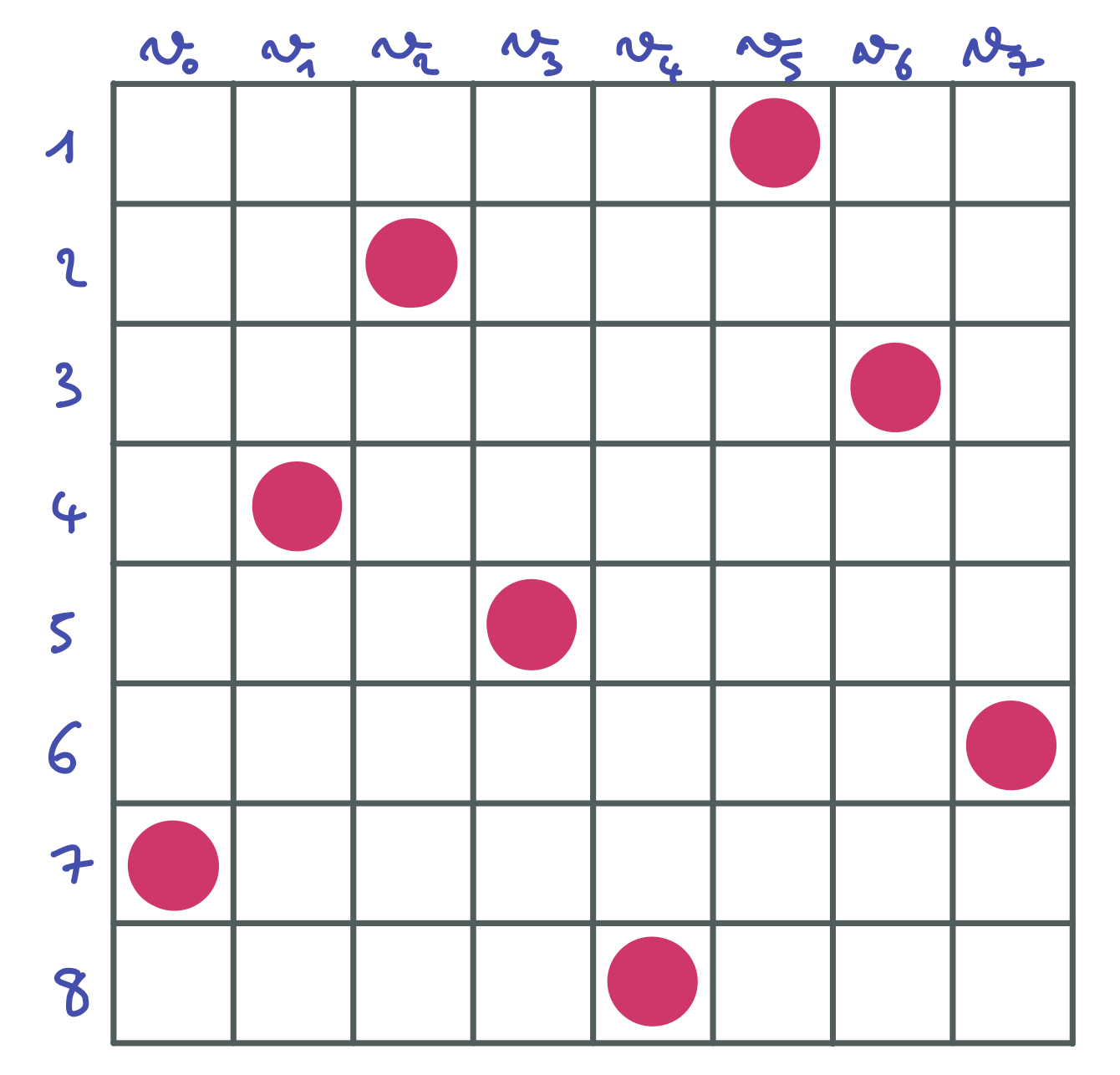
Exercices d’assimilation

A-ass-00

Le problème des reines en booléens. On modélise le problème des $N$ reines en utilisant uniquement des variables Booléennes. Le réseau de contraintes comporte $N^{2}$ variables, chacune associée à une case de l’échiquier. Voici par exemple les variables pour $N = 5$.

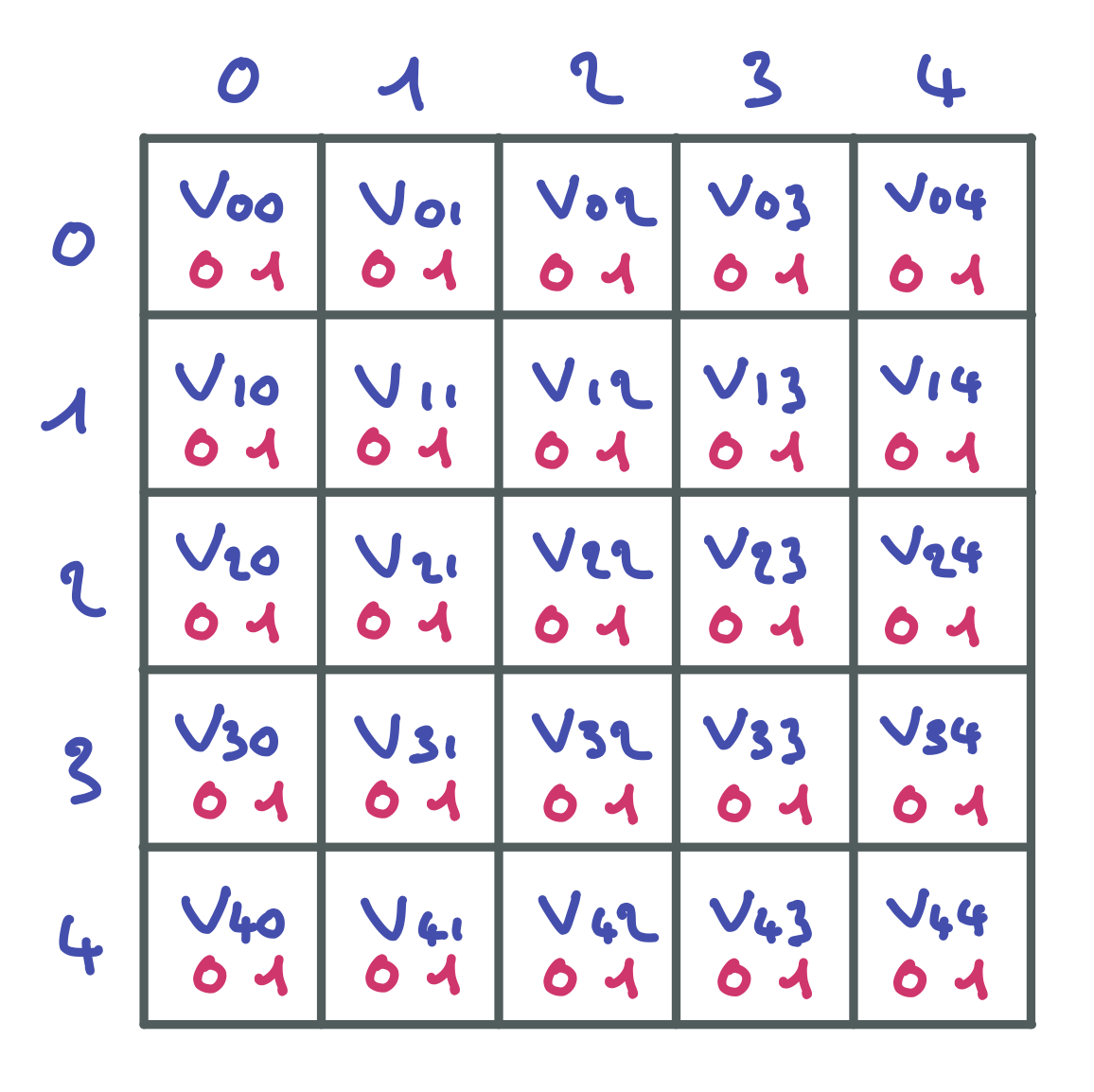
Une contrainte est associée à chaque ligne, chaque colonne et chaque diagonale de l’échiquier. Les contraintes relient toutes les variables d’une même ligne ou d’une même colonne expriment qu’une seule des variables concernées vaut 1. Les contraintes qui relient toutes les variables d’une même diagonale expriment qu’au plus une des variables concernées vaut 1.

Voici deux exemples de contraintes pour $N = 5$.

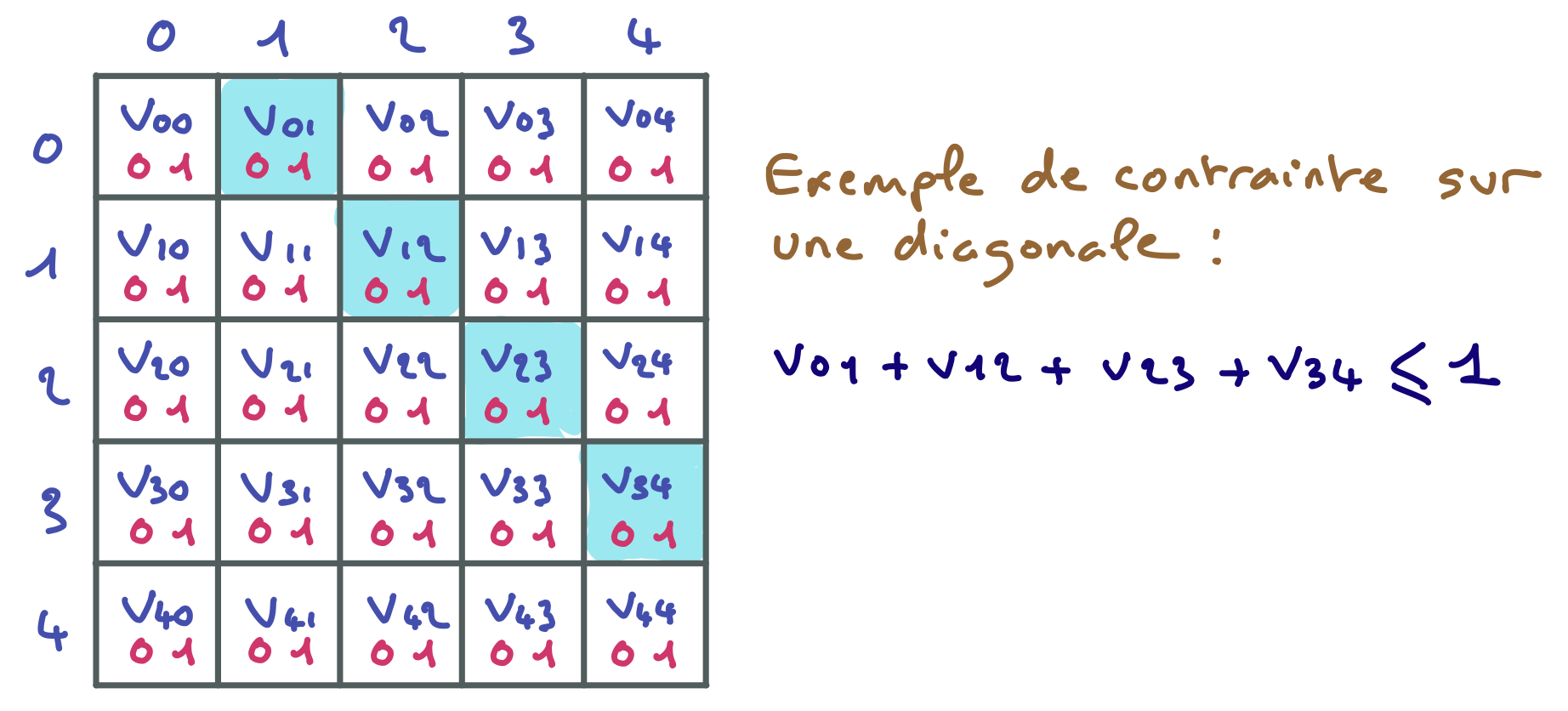
Réalisez une application CHOCO qui résout ce problème.

"Indice1"

La première chose à faire est de créer un modèle et de lui ajouter les variables du problème. Voici les lignes de code qui permettent de faire cela.

    int N = 8;

    //Création du modèle
    Model model = new Model(N + "-queens problem");

    // Création des variables
    IntVar[][] x = new IntVar[N][N];
    for(int i=0; i<N; i++)
    {
        for(int j=0; j<N; j++)
        {
            x[i][j] = model.intVar("X_"+i+"_"+j, 0, 1);
        }
    }

Voici les données créées en mémoire (dans le tas) par l’exécution de ces lignes de code.

"Indice2"

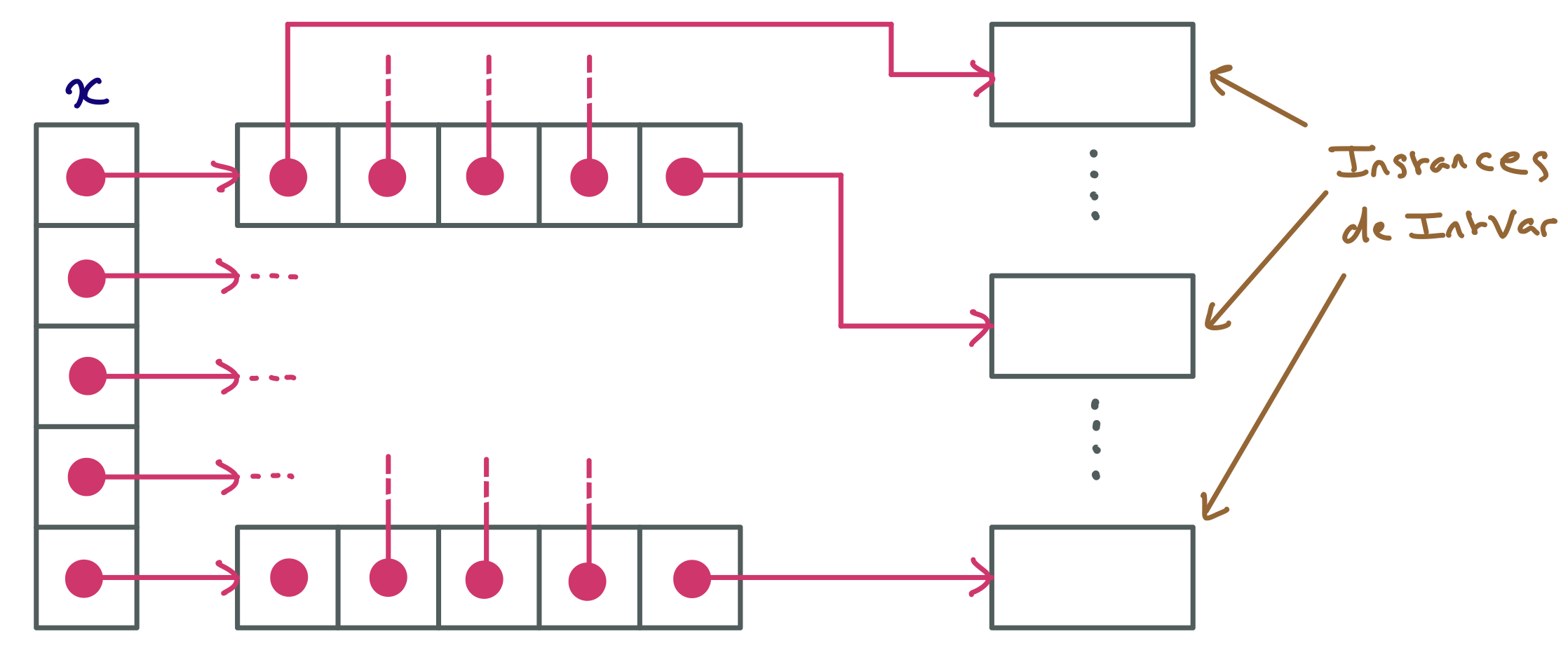
A présent il nous faut construire les contraintes. Commençons par les plus faciles, qui concernent les lignes de l’échiquier. En cherchant un peu dans la documentation CHOCO, on trouve une contrainte somme qui exprime que la somme de toutes les variables situées dans un tableau est égale à une valeur donnée (des variantes de cette contrainte permettent d’exprimer une inégalité $\leq ,\ \geq ,\ > ,\ <$ avec une constante ou une variable du réseau).

Pour construire une contrainte somme, les références des variables à prendre en compte doivent être dans un tableau. Ça tombe bien, les variables de chaque ligne de l’échiquier sont déjà dans des tableaux. Vous pouvez le vérifier en observant la figure donnée dans l’indice précédent. En java, chaque cellule d’un tableau à 2 dimensions contient la référence d’un tableau à une dimension.

Le code suivant permet de produire toutes les contraintes relatives aux lignes de l’échiquier.

    for(int i=0; i<N; i++)
    {
        model.sum(x[i], "=", 1).post();
    }

Dans la lignemodel.sum(x[i], "=" 1).post(), x[i] désigne un tableau de taille N dont les cellules contiennent les références des objets de type IntVar qui représentent les variables d’une ligne de l’échiquier.

"Indice3"

Après les lignes, il nous faut produire les contraintes relatives aux colonnes. Mais cette fois-ci, nous ne disposons pas de tableau tout fait contenant les références des variables d’une même colonne. Il faut donc, pour chaque colonne, créer un tel tableau et le remplir avant de l’utiliser pour créer une contrainte de type somme similaire à celles utilisées pour les lignes.

Voici les lignes de codes permettant de faire cela.

    for(int j=0; j<N; j++)
    {
        IntVar[] col = new IntVar[N];
        for(int i=0; i<N; i++)
        {
            col[i] = x[i][j];
        }
        model.sum(col, "=", 1).post();
    }

"Indice4"

Nous devons maintenant produire une contrainte pour chacune des $2N – 1$ diagonales montantes et des $2N – 1$ diagonales descendantes de l’échiquier. Il existe plusieurs moyens de collecter les variables de ces diagonales. Voici celui que je propose pour les diagonales montantes. Comme le montre la figure ci-dessous, on peut numéroter les diagonales montantes de 0 à $2N – 2$. Les cellules appartenant à la diagonale $i$ ont pour particularité que la somme de leurs indices vaut $i$. Par exemple, la cellule d’indice $(3,1)$ est sur la diagonale 4.

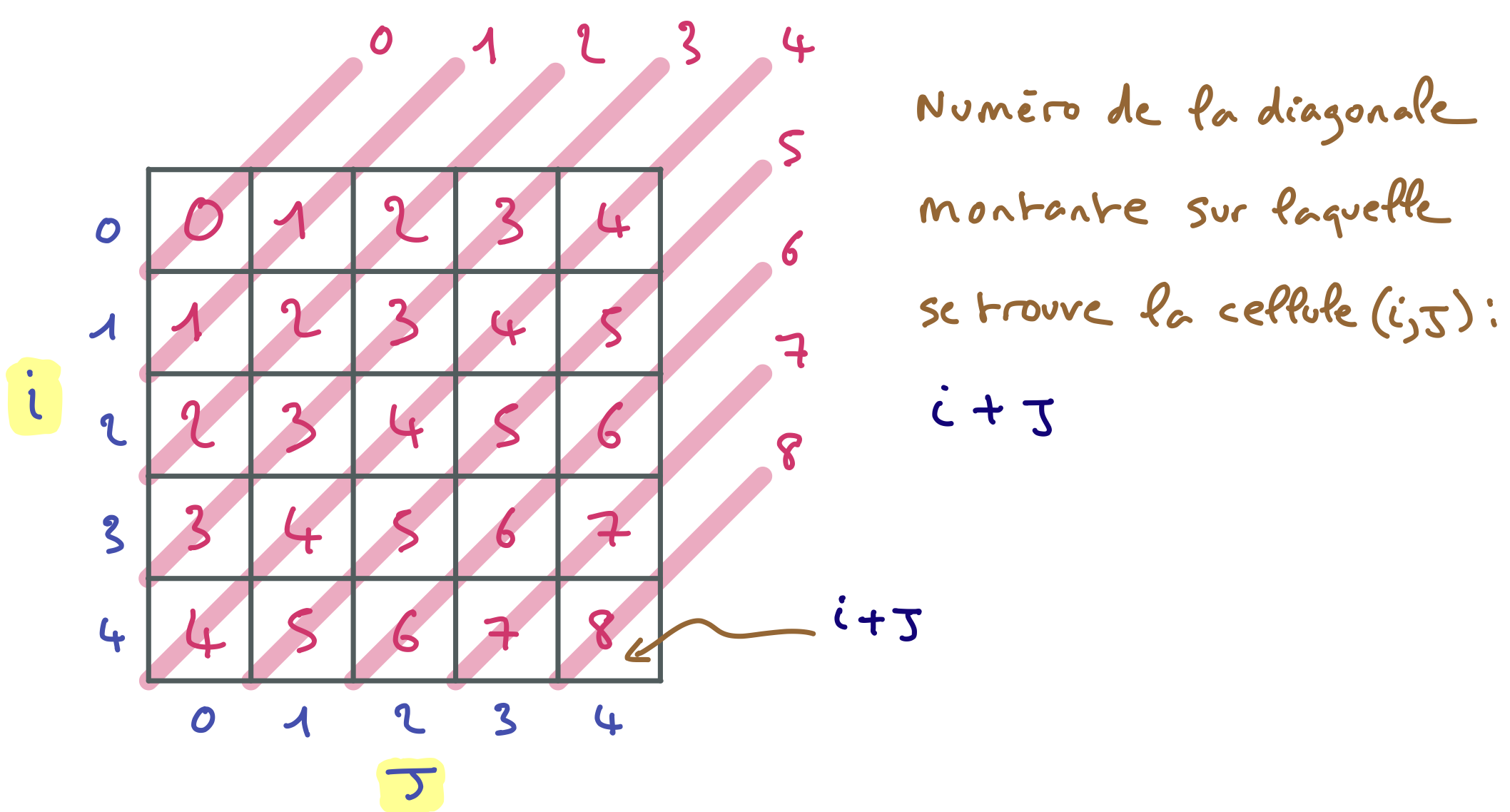
On peut créer les listes des variables des différentes diagonale en parcourant une seule fois toutes les cellules du tableau représentant l’échiquier. Pour ce faire, on crée un tableau dUp de $2n – 1$ listes initialement vides. On parcourt l’échiquier en faisant varier les indices $i$ et $j$ entre $0$ et $N – 1$ et pour chaque $(i,j)$ on ajoute la variable $x_{\text{ij}}$ à la liste dUp[i+j].

A l’issue du parcours, il suffit de parcourir le tableau dUp, de transformer chaque liste qu’il contient en un tableau de références d’objet de type IntVar représentant les variables d’une diagonale, et de produire une contrainte expriment que la somme de ces variables est inférieure ou égale à 1. Voici les lignes de code qui font cela.

    //Diagonales montantes
    ArrayList<IntVar>[] dUp = new ArrayList[2*N-1];

    for(int k=0; k<2*N-1; k++)
    {
        dUp[k] = new ArrayList<>();
    }

    for(int i=0; i<N; i++)
    {
        for(int j=0; j<N; j++)
        {
            dUp[i+j].add(x[i][j]);
        }
    }

    for(int k=0; k<2*N-1; k++)
    {
        IntVar[] tmp = dUp[k].toArray(new IntVar[0]);
        model.sum(tmp, "<=", 1).post();
    }

La première boucle crée les $2N – 1$ listes vides. La double boucle suivante parcoure toutes les variables et place chacune d’elles dans la liste qui représente la diagonale montante à laquelle elle appartient.

La dernière boucle récupère chaque liste de variable, la transforme en un tableau, crée une contrainte exprimant que la somme des variables de ce tableau est inférieure ou égale à 1, et enregistre cette contrainte dans le modèle.

Il ne reste plus qu’à produire les contraintes correspondant aux diagonales descendantes. Essayez de trouver vous-même le moyen de le faire en vous inspirant de la méthode qui vient d’être décrite pour les diagonales montante.

"Solution"

On peut numéroter les $2N – 1$ diagonale comme indiqué sur la figure ci-dessous. Une cellule de coordonnées $(i,j)$ appartient à la diagonale descendante numéro $i – j + N – 1$.

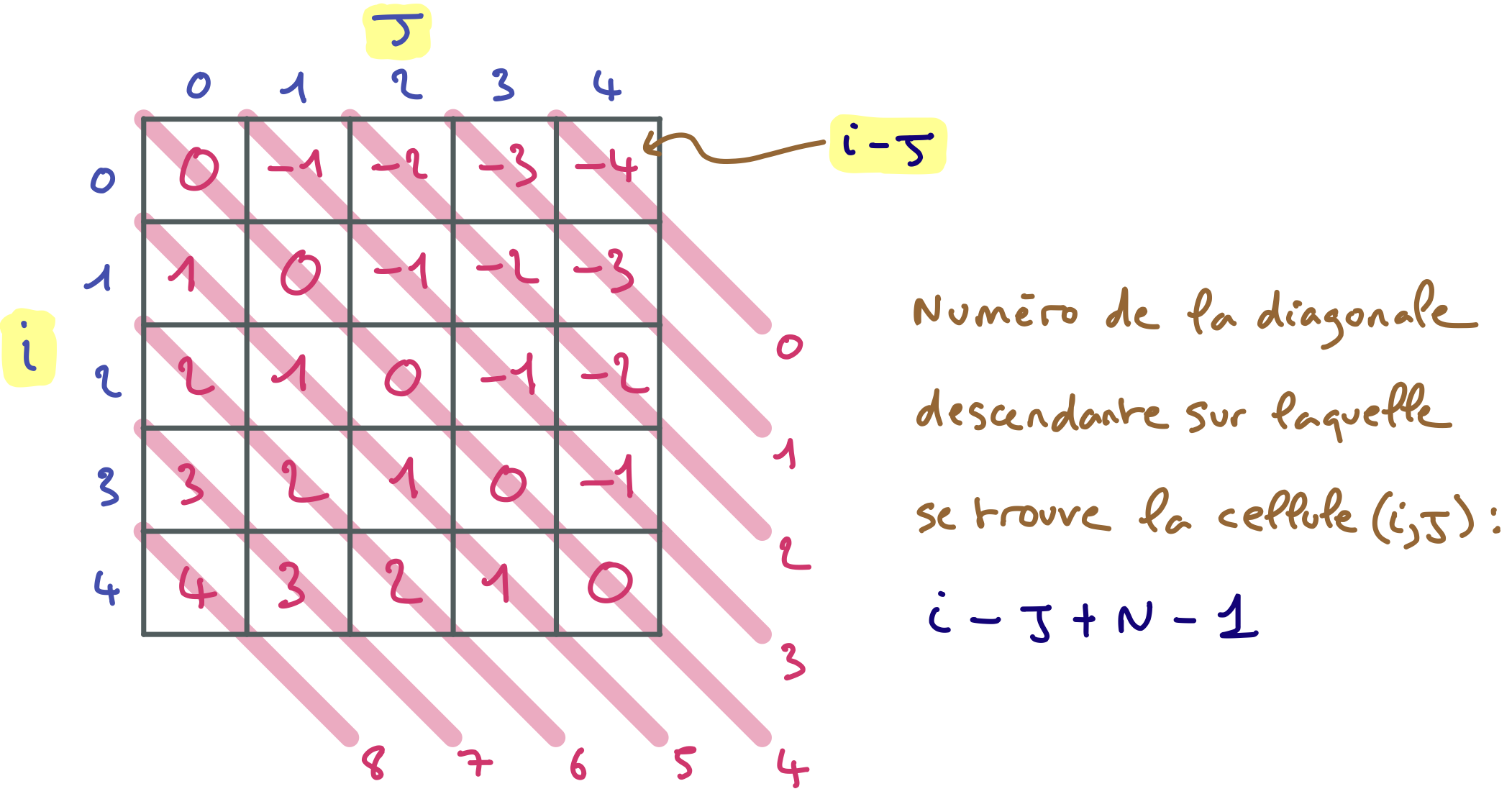
Cette observation étant faite, il devient facile d’implémenter la production des contraintes relatives aux diagonales descendantes.

    //Diagonales descendantes
    ArrayList<IntVar>[] dDown = new ArrayList[2*N-1];

    for(int k=0; k<2*N-1; k++)
    {
        dDown[k] = new ArrayList<>();
    }

    for(int i=0; i<N; i++)
    {
        for(int j=0; j<N; j++)
        {
            dDown[i-j+N-1].add(x[i][j]);
        }
    }

    for(int k=0; k<2*N-1; k++)
    {
        IntVar[] tmp = dDown[k].toArray(new IntVar[0]);
        model.sum(tmp, "<=", 1).post();
    }

Lorsque ces contraintes sont ajoutées au modèle, le reste du code est similaire à celui de l’exemple introductif.

    //Résolution
    Solution solution = model.getSolver().findSolution();
    if(solution != null)
    {
        System.out.println(solution.toString());
    }

A-ass-01

Le problème du sac à dos. Les données du problème sont les suivantes :

Deux entiers $W$ et $V$ représentant respectivement le poids maximum et la valeur minimum des objets à mettre dans un sac à dos.
Une liste $w_{0},\ldots w_{n – 1}$ des poids des objets susceptibles d’être mis dans le sac.
Une liste $v_{0},\ldots v_{n – 1}$ des valeurs des objets susceptibles d’être mis dans le sac.

Les variables du problème, $x_{0},\ldots,x_{n}$ ont toutes pour domaine {0,1}.

Les contraintes sont : $\sum_{i = 0}^{n – 1}{w_{i}\ x_{i}} \leq W$ et $\sum_{i = 0}^{n – 1}{\text{wv}{i}\ x{i}} \geq V$.

Réalisez une application CHOCO qui résout ce problème et testez-là avec l’instance suivante :

Poids des objets (en kg) : 2, 5, 7, 8, 15, 21, 23
Prix correspondants (en Euros) : 3, 11, 8, 10, 10, 8, 9
Valeur minimum des objets emportés : 40 Euros
Poids maximum des objets emportés : 50 Kgs

"Indice1"

Il faut définir les constantes représentant les données de l’instance de problème. On peut le faire de la manière suivante :

    int W = 50;
    int V = 40;
    int[] w = new int[]{2,5,7,8,15,21,23};
    int[] v = new int[]{3,11,8,10,10,8,9};

Dans une version plus sophistiquée de l’application, ces variables seraient initialisées par des données issues d’un fichier représentant l’instance à résoudre. A vous maintenant de définir le modèle et les variables.

"Indice2"

Le code permettant de définir et initialiser les variables est très proche de ce que nous avons déjà rencontré.

    //Création du modèle
    Model model = new Model("Backpack");

    // Création des variables
    int N = w.length;
    IntVar[] x = new IntVar[w.length];
    for(int i=0; i<N; i++)
    {
        x[i] = model.intVar("X_"+i, 0, 1);
    }

Il faut maintenant trouver le moyen de produire les contraintes. CHOCO dispose de contrainte de type $a_{0} x_{0} + \ldots + a_{n – 1} x_{n – 1} \ \text{op} \ b$ où, $a_{0}$ à $a_{n – 1}$ et $b$ sont des coefficients réels et $x_{0}$ à $x_{n – 1}$ des variables dont les domaines contiennent des entiers. Plusieurs possibilités existe pour l’opérateur op, telles que <, >, = etc.

Cette contrainte est produite par la méthode scalar de la classe Model. Consultez la documentation de CHOCO pour savoir comment utiliser cette méthode.