Partie A

Programmation procédurale en Java

Objectif

Savoir réaliser une application simple utilisant uniquement des méthodes statiques, des tableaux, des types scalaires, et des chaînes de caractères.

Prérequis

Une première expérience, même limitée, en programmation procédurale ou objet.

A1 : Un programme de découverte

Présentation

public class Decouverte
{
    public static void main(String[] args)
    {
        System.out.println("Bonjour");
    }
}

Tout programme est constitué de blocs qui s’imbriquent et / ou se succèdent. Ici nous avons deux blocs :

La classe Decouvertedont le code source doit être placé dans un fichier nommé Decouverte.java. Pour l’instant, nous pouvons voir une classe comme un un bloc contenant des méthodes et des variables. Les variables contiennent des données et les méthodes réalisent des traitements.
La méthode main est le point de départ de l’exécution de tout programme java.

Pour exécuter ce programme, vous pouvez utiliser un IDE (environnement intégré de développement) tel que NetBeans, IntelliJ IDEA, Eclipse… Mais vous devez aussi maîtriser la compilation et l’exécution d’un programme Java via une console. Cette démarche comporte en trois étapes.

Édition du programme avec l’éditeur de code source de votre choix.
Compilation du fichier source avec la ligne de commande javac Decouverte.java. Cela suppose qu’un environnement de développement appelé Java SDK soit installé sur votre machine et que les variables d’environnement soit configurées de manière à ce que l’exécutable javac, c’est à dire le compilateur java, soit accessible. Le résultat de la compilation est un fichier Decouverte.class.
Exécution du fichier résultant de la compilation par la ligne de commande java Decouverte.

Plusieurs mots-clés interviennent dans la définition de la méthode main.

public static void main(String[] args)
{
    ...
}

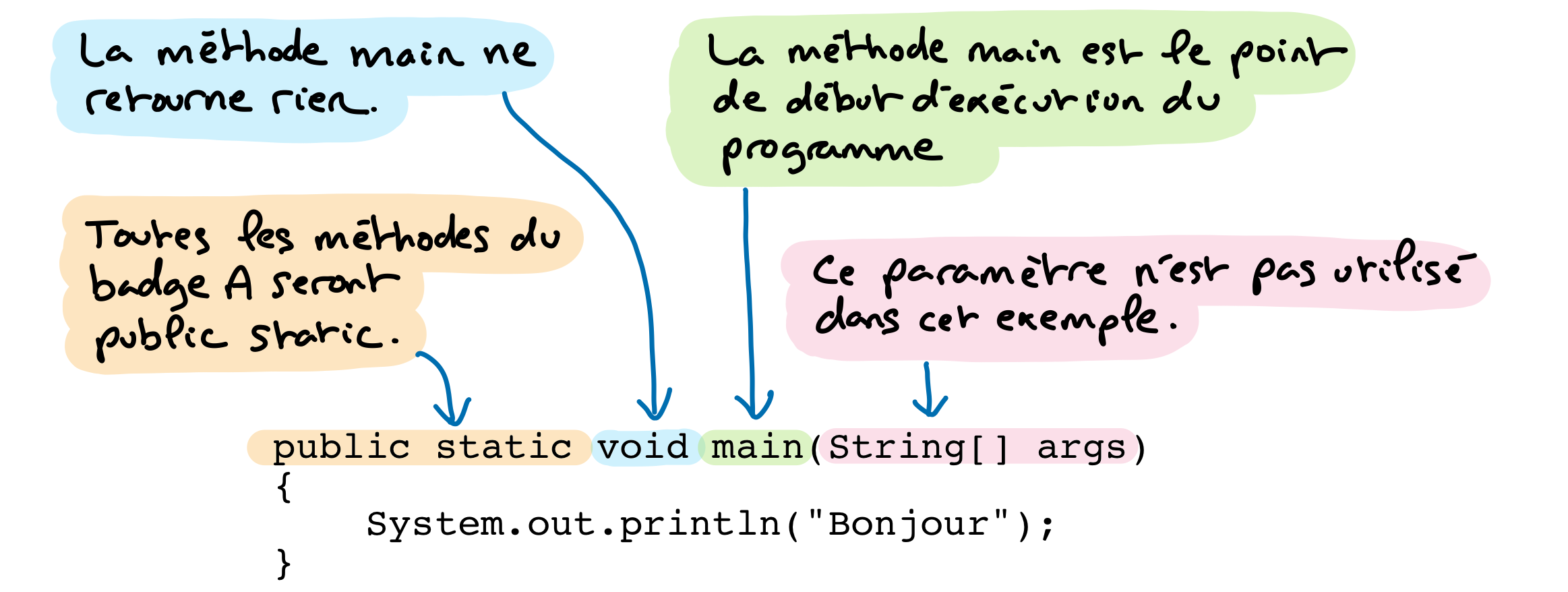
public : Toutes les méthodes du badge A seront public. Nous introduirons plus tard d’autres options, à partir de la partie B.
static : Toutes les méthodes de la partie A seront static. De telles méthodes sont aussi appelées méthodes de classe. Nous introduirons d’autres sortes de méthodes dans la partie B.
void : Signifie que la méthode main ne retourne rien.
main : La méthode principale d’un programme java porte toujours ce nom, tout comme elle est toujours public, static, et a toujours un paramètre de type String[].
Le paramètre String[] args peut permettre à la méthode main de prendre en compte des arguments passés par la ligne de commande lors de l’appel du programme depuis la console. Dans notre exemple, cette possibilité n’est pas exploitée.

Exercices de découverte

A-dec-10

Répondez aux questions suivantes :

Quelle est la première méthode exécutée par un programme Java ?
Que retourne la méthode main?
Quel est le rôle de la méthode System.out.println?
Qu’est-ce que le SDK de Java ?
Quel est le nom du compilateur java ?

"Solutions"

main
rien (void).
afficher quelque chose à l’écran
L’ensemble des ressources permettant de développer des programmes Java.
javac

A2 : Un programme qui compte

Présentation

Voici notre deuxième programme. Autant que possible, testez sur machine les différents programmes qui seront présentés et tentez quelques modifications pour vérifier que vous êtes capable de prévoir leur effets. Le code des deux méthodes suivantes doit être placé dans la classe Decouverte.

    public static void compte(int k)
    {
        for(int i=0; i<k; i++)
        {
            System.out.println(i);
        }
    }

    public static void main(String[] args)
    {
        compte(10);
    }

La méthode main appelle la méthode compte en lui passant en argument la valeur 10. La méthode compte reçoit cette valeur dans la variable k qui est le paramètre de la méthode compte. Lors du début de l’exécution de compte, la variable k est initialisée avec la valeur 10.

Il y a dans le code de la méthode compte une autre variable nommée i, à laquelle l’instruction for donne successivement les valeurs de 0 à k. L’exécution de la méthode a donc pour effet l’affichage des valeurs 0 à 9, avec un passage à la ligne entre chaque valeur.

La méthode compte peut être réécrite en utilisant l’instruction while au lieu de for.

    public static void compte(int k)
    {
        int i = 0;
        while(i<k)
        {
            System.out.println(i); 
            i++;
        }
    }

Les variables k et i sont appelée variables de méthodes ou variables automatiques. Elles n’existent que pendant l’exécution de la méthode dans laquelle elle sont déclarée et seul cette méthode peut les utiliser. La variable k a un rôle particulier puisque c’est un paramètre de la méthode. Sa valeur initiale est déterminée lors de l’appel de la méthode.

Exercices de découverte

A-dec-20

Si on remplace System.out.println(i) par System.out.print(i + " ") dans la méthode compte, on obtient l’affichage 0 1 2 3 … k (les valeurs sont séparées par des espaces. Modifiez le programme pour obtenir l’affichage 0, 1, 2, 3, …, k (sans virgule après la dernière valeur affichée).

"Solution"

public static void compteBis(int k)
{
    for(int i=0; i<k; i++)
    {
        System.out.print(i);
        if(i < k-1) System.out.print(", ");
        else System.out.println();
    }
}

D’autre variantes sont possibles et correctes. Vous pouvez tester la votre sur machine.

A-dec-21

Réalisez une méthode void compte(int a, int b) qui affiche tous les entiers compris entre a et binclus, séparés par des espaces. Par exemple, l’appel compte(3, 6) doit afficher 3 4 5 6.

"Solution"

public static void compte(int a, int b)
{
    for(int i=a; i<=b; i++)
    {
        System.out.print(i + " ");
    }
    System.out.println();
}

A-dec-22

Complétez le code ci-dessous pour qu’un appel de la méthode couples(a,b) aie pour effet l’affichage de tous les couples de valeurs comprises entre a et b inclus. Par exemple, l’exécution de couples(4,5) devra afficher :

(4, 4)
(4, 5)
(5, 4)
(5, 5)

    public static void couples(int a, int b)
    {
        for(---------------------------)
        {
            for(---------------------------)
            {
                System.out.println("( " + i + " , " + j + " )" );
            }
        }
    }

"Solution"

public static void couples(int a, int b)
{
    for(int i=a; i<=b; i++)
    {
        for(int j=a; j<=b; j++)
        {
            System.out.println("( " + i + " , " + j + " )" );
        }
    }
}

A3 : Utiliser des tableaux

Présentation

En java comme dans bien d’autres langages de programmation, un tableau est une collection de données de même type stockées de manière contigüe en mémoire dans des cellules désignées par des indices. Tous les exemples de code qui seront introduits sont supposés se trouver dans la classe Decouverte.

Voici un exemple de création d’un tableau de 10 entiers.

private static int[] tab = new int[10];

Il y a beaucoup de choses à dire et à comprendre à propos de cette ligne. Tout d’abord, elle ne se trouve pas dans la définition d’une méthode, mais directement dans une classe, en l’occurrence la classe Decouverte. Comme sa déclaration n’est pas dans une méthode, tab n’est pas une variable de méthode. Il s’agit d’une variable de classe comme nous l’indique le mot clé static. Ceci signifie que ce tableau existe pendant toute la durée de l’exécution du programme et pas seulement pendant la durée d’exécution d’une méthode particulière comme c’est le cas pour une variable de méthode. Le modificateur d’accès private indique que seule les méthodes de la classe Decouverte y ont accès.

Ensuite il faut comprendre que la ligne de code ci-dessus peut se décomposer en deux lignes ayant chacune un rôle différent.

private static int[] tab;
tab = new int[10];

La première ligne déclare une variable nommée tab de type int[]. Cette variable est située dans une zone mémoire dédiée aux variables de classe. Cette variable peut contenir la référence d’un objet de type int[]. Techniquement, une référence est une adresse mémoire à laquelle est situé un objet dans une zone mémoire appelée tas. La notion d’objet sera détaillée plus tard. La seule chose que nous devons savoir à ce sujet pour le moment est qu’en java, tout tableau est un objet.

La deuxième ligne crée un tableau d’entiers de 10 cellules, situé dans le tas. Chaque cellule contient la valeur 0. Voici la représentation graphique du résultat.

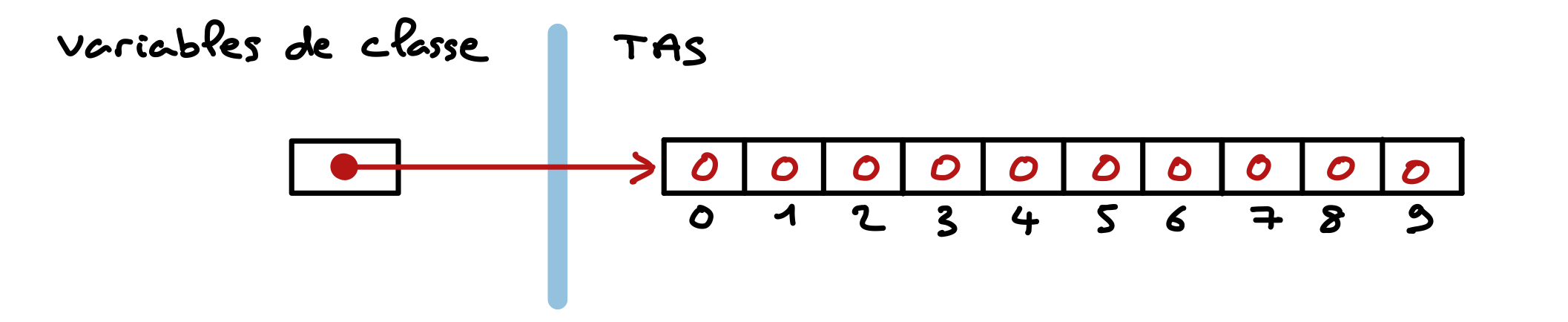
Nous allons maintenant réaliser une méthode permettant d’afficher le contenu d’un tableau d’entiers.

    public static void printTabInt(int[] t)
    {
        for(int i=0; i< t.length; i++)
        {
            System.out.print(t[i] + " ");
        }
        System.out.println();
    }

On voit que cette méthode a un paramètre t de type int[], c’est à dire une référence d’un tableau d’entiers. La notation t.length permet de récupérer la longueur du tableau t. La notation t[i] désigne la valeur située dans la cellule d’indice i du tableau t.

Voici un exemple d’appel de la méthode printTabInt depuis la méthode main.

    public static void main(String[] args)
    {
        tab[1] = 5; tab[3] = 7;
        printTabInt(tab);
    }

L’exécution de cette méthode a pour effet l’affichage 0 5 0 7 0 0 0 0 0 0.

Exercices de découverte

A-dec-30

Réalisez une méthode Rempli0123 qui accepte en paramètre la référence d’un tableau d’entiers et qui rempli ce tableau d’entiers avec les valeurs 0, 1, 2, etc. La valeur placée dans la dernière cellule devra donc être égale à la longueur du tableau moins 1.

"Solution"

public static void rempli0123(int[] t)
{
    for(int i=0; i< t.length; i++)
    {
        t[i] = i;
    }
}

Réalisez une méthode main qui teste la méthode Rempli0123 en remplissant le tableau désigné par la variable de classe tab que nous avons créé précédemment puis en affichant le contenu de ce tableau à l’aide de la méthode printTabInt.

"Solution"

public static void main(String[] args)
{
    rempli0123(tab); printTabInt(tab);
}

A4 : La pile et le tas

Présentation

Examinons la méthode suivante.

    public static int[] produitab(int a, int b)
    {
        int[] t = new int[b-a+1];
        for(int i=0; i< t.length; i++)
        {
            t[i] = a + i;
        }
        return t;
    }

Contrairement aux méthodes précédentes qui ne retournaient rien (void), celle-ci retourne la référence d’un tableau d’entiers (int[]) qui, incidemment, n’existe pas encore au moment de l’appel de la méthode. Examinons les différents blocs.

Le premier bloc est la ligne suivante.

				int[] t = new int[b-a+1];

Elle a pour effet de déclarer une variable de méthode t et d’y placer la référence d’un tableau d’entiers de taille b-a+1 qui, comme tout tableau est situé dans le tas. Le nombre de cellules de ce tableau, b-a+1, permet de stocker tous les entiers compris entre a et b. Essayez avec un exemple, par exemple a = 3 et b = 7, pour vous en convaincre.

Le deuxième bloc est la boucle suivante.

        for(int i=0; i< t.length; i++)
        {
            t[i] = a + i;
        }

Elle a pour effet de remplir le tableau précédemment créé. Voici par exemple l’état de la mémoire à la fin de son exécution pour des arguments 3 et 7 passés en paramètres de la méthode.

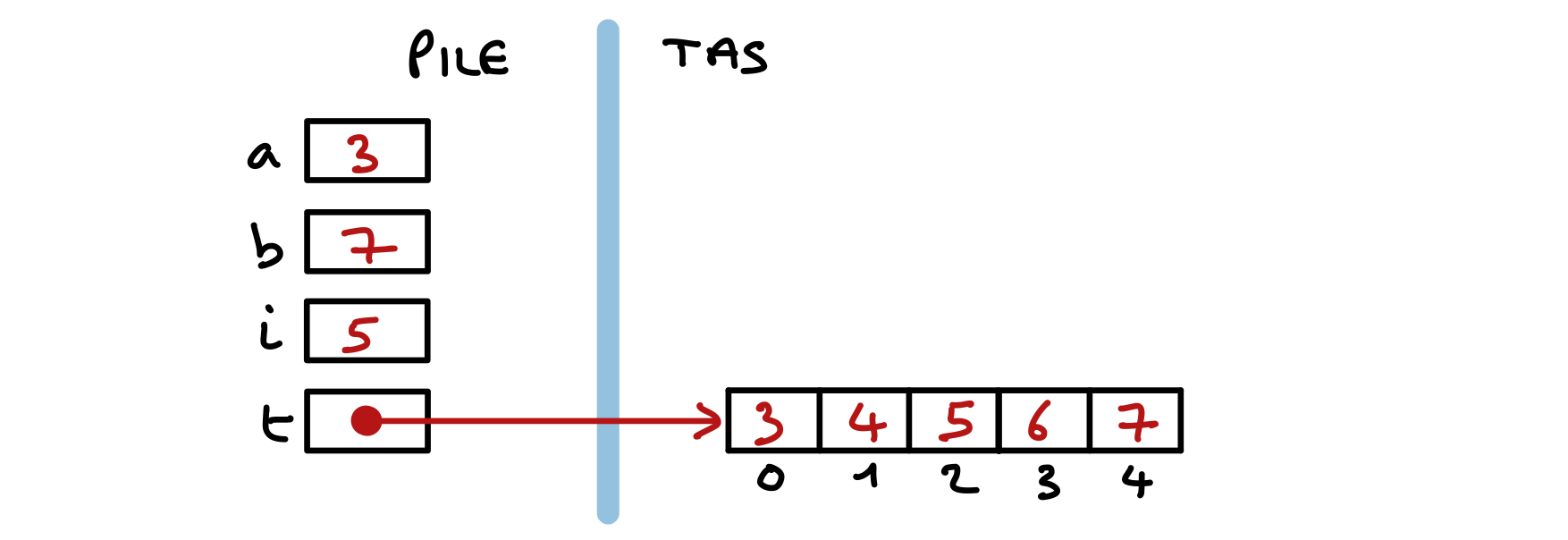
On y voit les 4 variables de méthodes, dont deux sont des paramètres, situées dans une mémoire appelée pile. Ces quatre variables n’existeront plus après l’exécution de la méthode (et seront recréées automatiquement à chaque nouvelle exécution). Par contre, le tableau, situé dans le tas, continuera d’exister tant que sa référence sera contenue dans au moins une variable.

Pour illustrer le cycle de vie du tableau, appelons la méthode main de la classe Decouverte suivante.

class Decouverte
{
    private static int[] tab = new int[10];
  
    public static void printTabInt(int[] t)
    {
        for(int i=0; i< t.length; i++)
        {
            System.out.print(t[i] + " ");
        }
        System.out.println();
    }
  
    public static int[] produitab(int a, int b)
    {
        int[] t = new int[b-a+1];
        for(int i=0; i< t.length; i++)
        {
            t[i] = a + i;
        }
        return t;
    }
  
    public static void main(String[] args)
    {
        tab = produitab(3,7);
        printTabInt(tab);
    }
}

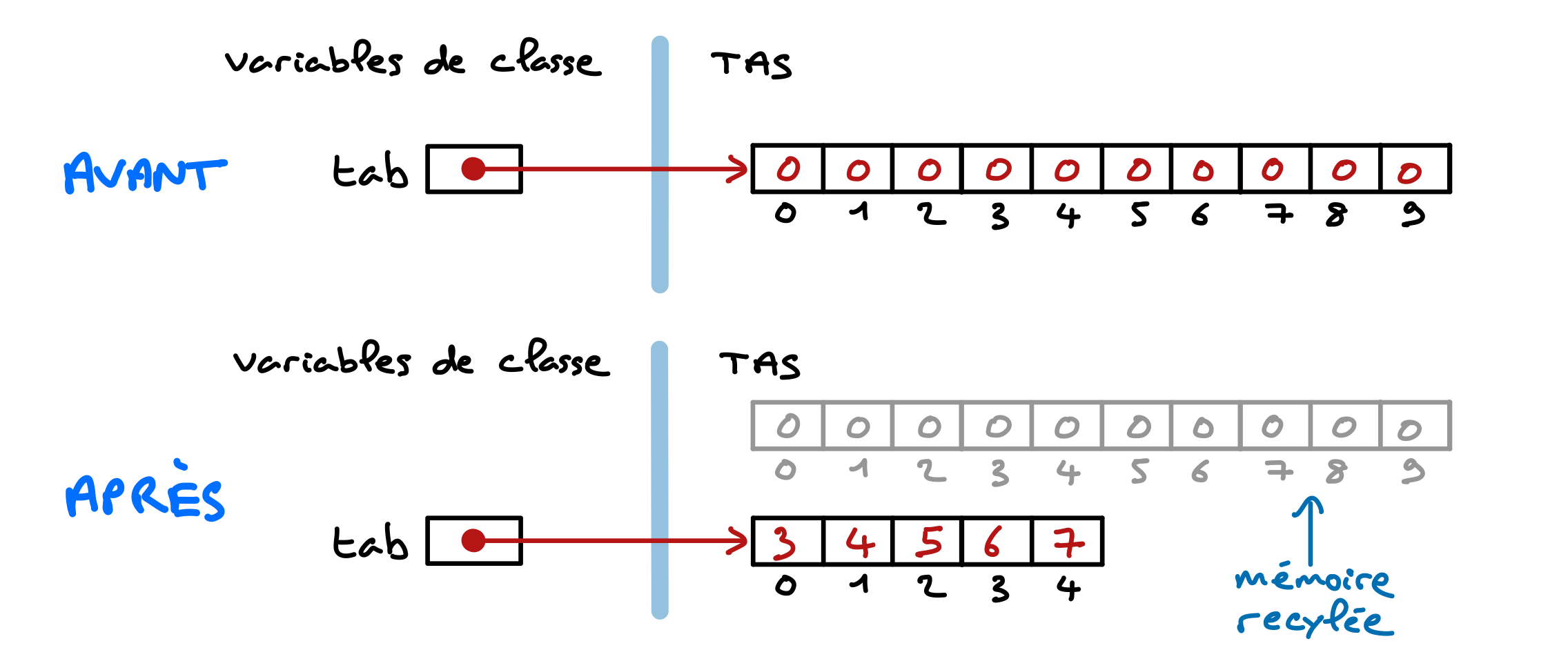
Lors de l’exécution de main il se passe plusieurs choses très intéressantes et qu’il est important que vous preniez le temps de comprendre. L’initialisation des variables de classe se fait avant l’exécution de main. Donc dès le début de cette exécution tab désigne un tableau dont les 10 cellules contiennent 0.

L’appel produitab(3,7) crée un nouveau tableau dans le tas et en retourne la référence qui remplace celle précédemment contenue dans la variable de classe tab. Donc l’ancien tableau désigné par tab n’est plus pointé par aucune variable. Il sera automatiquement détruit par un dispositif de recyclage de la mémoire appelé ramasse miettes. L’appel à printTabInt affiche le contenu du nouveau tableau, qui sera lui même détruit à l’issue de l’exécution de main.

Exercices de découverte

A-dec-40

Dans l’exemple précédent, la variable de classe tab désigne initialement un tableau remplis de 0 qui ne sert à rien puisqu’il est détruit automatiquement par le ramasse miette sans jamais être utilisé. Quelle modification faut-il faire pour éviter la création de ce tableau inutile ?

"Solution"

public static int[] tab;

A-dec-41

Dans la classe Decouverte présentée précédemment, la variable de classe tab permet de récupérer le résultat de l’appel de la méthode produitab qui sera ensuite transmis à la méthode printTabInt. Mais il n’est pas nécessaire d’utiliser une variable de classe pour faire cela. Modifiez le code de la classe Decouverte de manière à ce que la variable tabsoit une variable de méthode de main. Dans cette nouvelle version, il ne doit plus y avoir de variable de classe.

"Solution"

class Decouverte
{ 
    public static void printTabInt(int[] t)
    {
        // Aucun changement
    }
  
    public static int[] produitab(int a, int b)
    {
        // Aucun changement
    }
  
    public static void main(String[] args)
    {
        int [] tab = produitab(3,7);
        printTabInt(tab);
    }
}

A-dec-42

Réécrivez la méthode mainde la classe Decouverte de manière à ce que son exécution ait le même effet que la version précédente, mais sans utiliser aucune variable (ni de méthode, ni de classe).

"Solution"

public static void main(String[] args)
{
    printTabInt(produitab(3,7));
}

A5 : Types primitifs et chaînes de caractères

Présentation

Dans exemple précédent, nous avons utilisé des valeur et variable de type int, qui représente des entiers relatifs. int est un type primitif, qui représente une donnée simple. On parle parfois de type scalaire. Voici quelques types primitifs de java.

int : entiers signés entre $−2^{31}$ et $2^{31} − 1$.
long : entiers signés entre $−2^{63}$ et $2^{63} − 1$.
char : caractère imprimable
byte : entier compris entre -128 et 127
float : nombre en virgule flottante codé sur 4 octets
double : nombre en virgule flottante codé sur 8 octets
boolean : valeur Booléenne (true ou false)

Un autre type standard très utilisé est le type String qui permet la représentation des chaînes de caractères. Tout comme les tableaux, les chaînes de caractères sont des objets. Mais pour l’instant, nous les considérons comme de simples structures de données.

Voici quelques exemples de création de chaînes (on suppose que ces lignes de code sont situées dans une méthode) :

String s1 = "Tom";
String s2 = "Tim";
String s3 = s1;

Et voici l’état des lieux en mémoire après l’exécution de ces lignes.

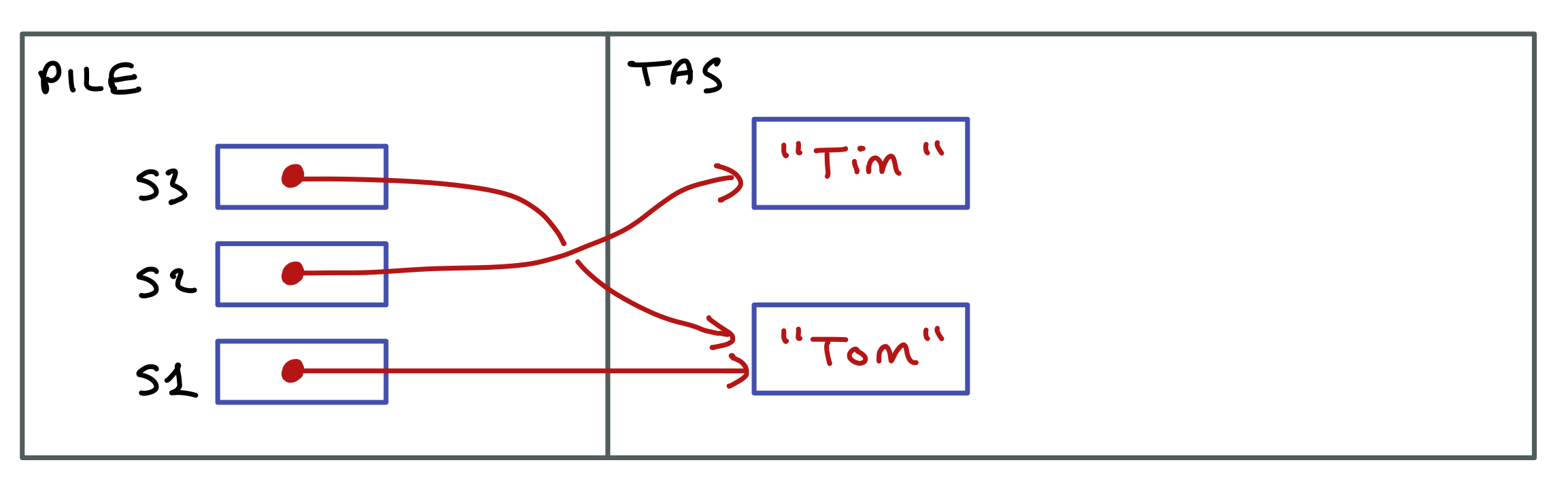
Les chaînes de caractères sont des objets situés dans le tas. Ce sont des instances de la classe String. Généralement, tout objet est créé à l’aide de l’opérateur new, mais dans cet exemple il est implicite. Il n’en reste pas moins que les variables s1, s2 et s3 contiennent des références qui désignent des objets de type String situés dans le tas. L’instruction s3 = s1 n’a pas dupliqué la chaîne désignée par s1 mais a juste recopié la référence de cette chaîne dans s3.

Ajoutons une quatrième ligne.

s1 = s1 + s2;

Le résultat en mémoire est le suivant.

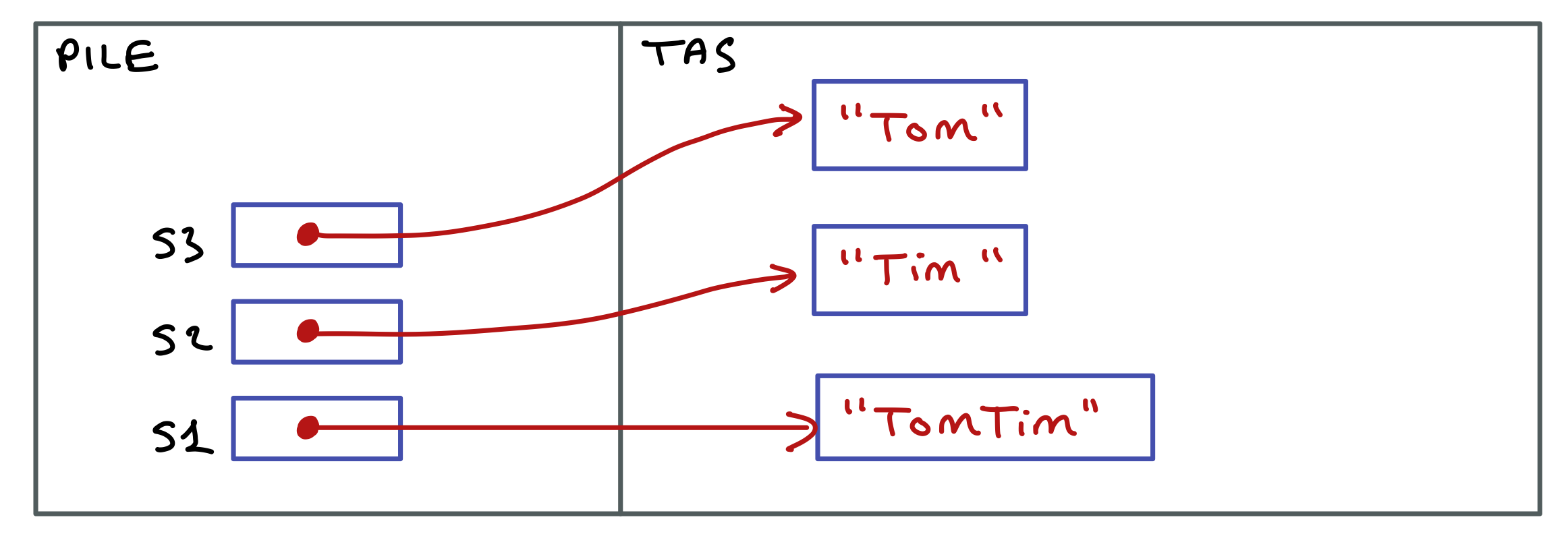
L’opérateur + n’a pas ajouté "Tim" à la fin de la chaîne désignée par s1, comme on pourrait le penser à l’issue d’une observation superficielle !

Cet opérateur a en fait créé une nouvelle chaîne résultant de la concaténation des chaînes désignées par s1 et s2, et la référence de cette nouvelle chaîne a été placée dans la variable s1.

La nuance est extrêmement importante. Si vous ne la saisissez pas, c’est qu’un pan entier de la programmation en Java vous échappe encore, et vous devez revenir sur les explications précédentes et / ou questionner un enseignant ou un expert pour bien saisir la subtilité. À défaut, vous pourrez produire, dans des applications que vous développerez, des bugs que vous ne comprendrez pas.

Exercices de découverte

A-dec-50

Après les lignes de code données en exemple précédemment, on écrit :

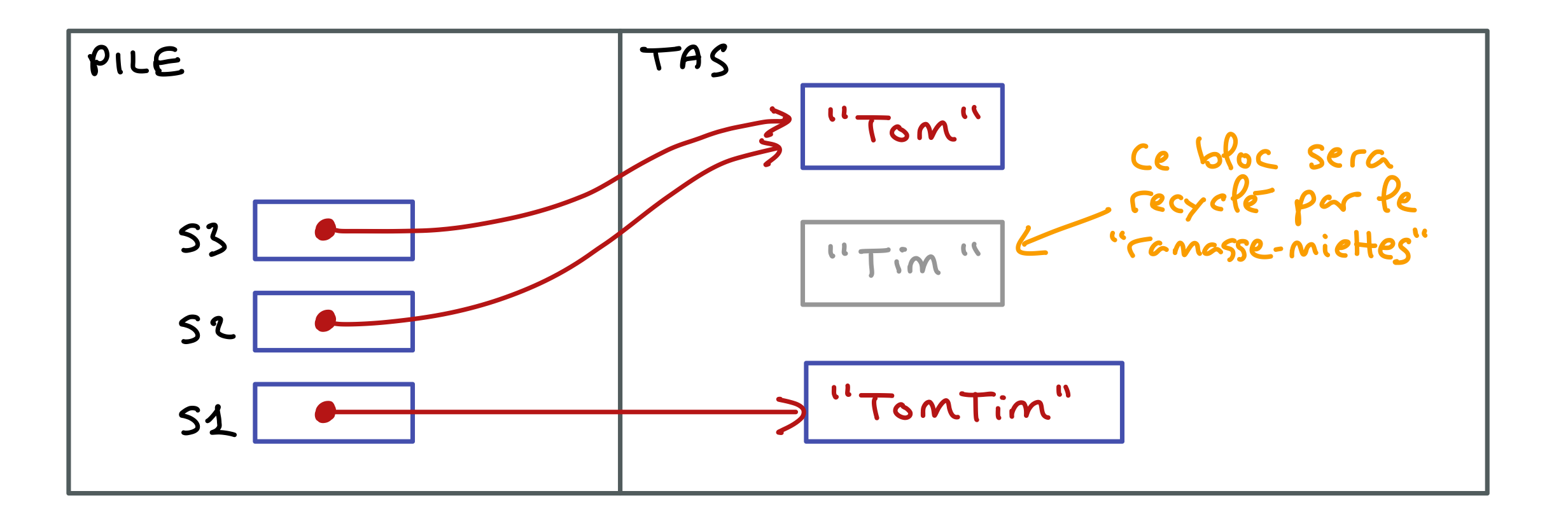
s2 = s3;

Dessinez la configuration en mémoire après l’exécution de cette ligne. Que devient le bloc mémoire contenant "Tim" ?

"Solution"

A-dec-51

Dans une même classe (par exemple Decouverte), on place les méthodes suivantes.

    public static void modif(String s)
    {
        s = s + s;
    }

    public static void main(String[] args)
    {
        String t = "Tim"; 
        modif(t); 
        System.out.println(t);
    }

Voici la configuration en mémoire au tout début de l’exécution de la méthode modif, juste avant l’exécution de la ligne s = s + s.

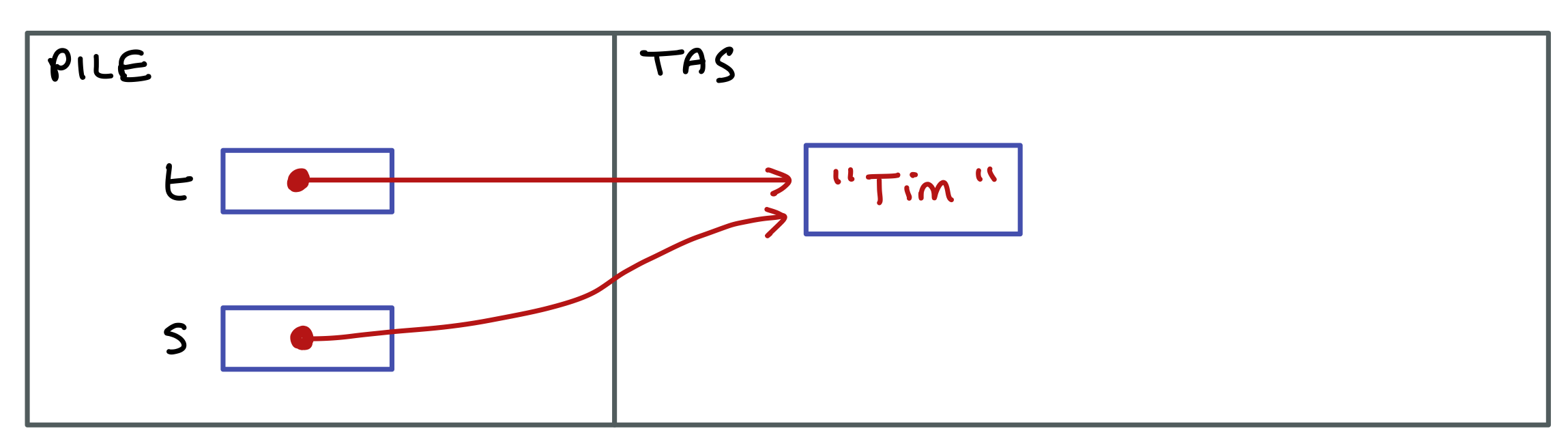
Dessinez la configuration en mémoire à la fin de l’exécution de la méthode modif, juste après l’exécution de la ligne s = s + s. Déduisez-en ce qui est affiché par l’exécution de main.

"Solution"

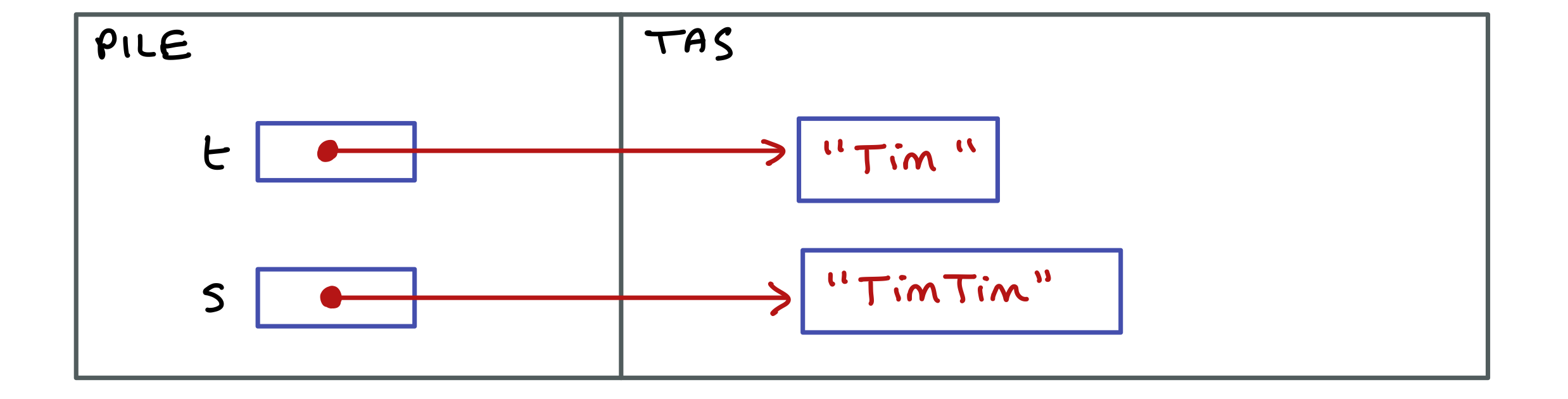
Le programme affiche Tim. L’exécution de la méthode a été sans effet sur la chaîne désignée par la variable de méthode t de main. La chaîne "TimTim" créée par la méthode modif sera détruite par le ramasse-miettes de Java sans avoir jamais été utilisée.

A6 : Ligne de commande

Présentation

Pour exécuter un programme Java directement depuis une console, vous devez taper java nom_du_programme. Mais il est possible d’ajouter des arguments, séparés par des espaces, comme par exemple :

java calc 10 + 20

Le programme calc récupérera ces arguments sous forme de chaînes de caractères dans le tableau args de sa méthode main. Voici une premier programme expérimental

public class Calc
{
      public static void main(String[] args)
      {
          for (String s : args)
          {
              System.out.println(s);
          }
			} 
}

Après compilation on tape dans la console :

java calc 10 + 20

Et on obtient l’affichage :

10 
+ 
20

Pour comprendre ce qui c’est passé, observons la configuration en mémoire juste avant la fin de l’exécution.

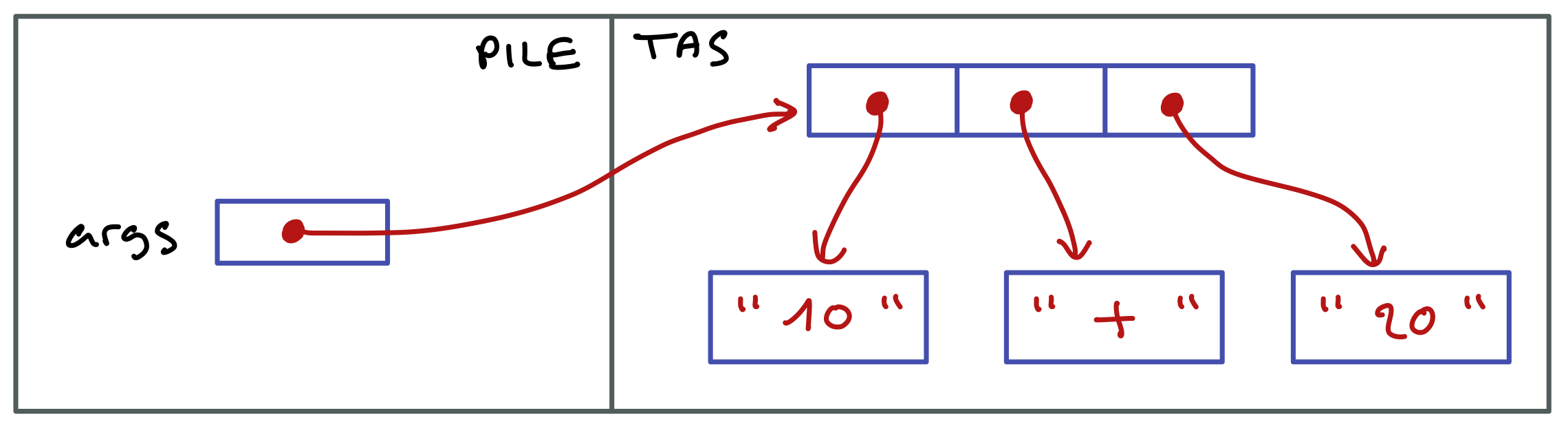
On constate que les arguments passés en ligne de commande ont été placé dans un tableau de chaînes de de caractères. Techniquement, les cellules d’un tel tableau contiennent des références d’objets de types String situés dans le tas.

Tentons une première version d’un programme qui se comporte comme une calculatrice rudimentaire limitée à l’addition.

public class Calc
{
    public static void main(String[] args)
    {
        if((args.length != 3) || !args[1].equals("+"))
        {
            System.out.println("Arguments incorrects"); 
        }
        else
        {
            System.out.println(args[0] + args[2]);
        } 
    }
}

On lance l’exécution du programme depuis la console avec les arguments suivants…

java calc 10 + 20

… et on obtient l’affichage 1020 et non 30 comme attendu de la part d’une calculatrice. La raison est très simple à comprendre. L’opérateur + a été utilisé avec deux chaînes de caractères, la chaîne "10" et la chaine "20". Dans ce contexte, l’opération réalisée est une concaténation et non une addition. Pour faire une addition, il faut traduire nos chaînes en nombres.

public static void main(String[] args)
{
    if((args.length != 3) || !args[1].equals("+"))
    {
        System.out.println("Arguments incorrects"); 
    }
    else
    {
        int a = Integer.parseInt(args[0]); 
        int b = Integer.parseInt(args[2]);
        System.out.println(a+b); 
    }
}

Cette fois-ci, le programme se comporte comme attendu. L’exécution de la ligne de commande décrite précédemment a bien pour effet l’affichage de 30.

Évidemment, le programme ne fonctionne que si le premier et le troisième arguments ont un format permettant de les interpréter comme des entiers. Si on tape…

calc 10 + vingt

… on obtient un message d’erreur qui nous parle d’une exception. Nous verrons plus tard comment gérer cela.

Exercices de découverte

A-dec-60

Améliorez le programme précédent de manière à ce qu’il puisse réaliser une addition ou une multiplication.

"Solution"

public static void main(String[] args)
{
    if( (args.length != 3) || !(args[1].equals("+") || args[1].equals("*")) )
    {
        System.out.println("Arguments incorrects"); 
    }
    else
    {
        int a = Integer.parseInt(args[0]); int b = Integer.parseInt(args[2]);
        if(args[1].equals("+"))
        {
            System.out.println(a + b);
        }
        else
        {
            System.out.println(a * b);
        }
    }
}

Exercices d’assimilation

A-ass-00

On peut classer les entiers naturels (0, 1, 2, 3, …) en deux catégories : les nombres premiers et les nombres composés. Un entier $x$ est premier si et seulement s’il n’a pas d’autre diviseur que lui même et 1. Dans le cas contraire, il est composé, ce qui implique qu’il existe au moins deux entiers $a>$1 et $b>$ 1 tels que $x=ab$.

Pour savoir si un entier naturel $x$ est premier ou composé, on peut rechercher s’il a un diviseur $a$ compris entre 2 et $\lfloor \sqrt x \rfloor$. En effet, il est impossible qu’un entier $x$ soit le produit de deux entiers supérieurs à $\sqrt x$. La démonstration est laissée à la discrétion du lecteur, si affinité. Par exemple, si je veux savoir si 103 est premier, il me suffit d’essayer de la diviser par les entiers 2 à 10. Comme chacune des divisions a un reste non nul, 103 est premier.

Pour savoir si la division d’un entier $x$ par un entier $a$ a un reste, on peut utiliser l’opérateur modulo, noté %, qui donne le reste de la division $a/b$. Par exemple, 103 % 5 a pour résultat 3. Autre information utile : pour placer dans une variable borne de type int la valeur $\lfloor \sqrt x \rfloor$, on peut écrire borne = (int)Math.sqrt(x).

Sachant tout cela, réalisez une méthode de classe qui accepte en paramètre un entier supposé positif ou nul et qui retourne un Booléen valant true si et seulement si x est premier.

    public static boolean premier(int x)
    {
        // À compléter
    }

"Indice"

    public static boolean premier(int x)
    {
        if(x<2) return false;

        int borne = (int)Math.sqrt(x);

        for(int d=2; d <= borne; d++) 
        {
            // À compléter
        }

        return true;
    }

"Solution"

    public static boolean premier(int x)
    {
        if(x<2) return false;

        int borne = (int)Math.sqrt(x);

        for(int d=2; d <= borne; d++) // au lieu de <x
        {
            if(x % d == 0) return false;
        }

        return true;
    }

A-ass-01

Réalisez une méthode de classe premiers qui accepte en paramètre un entier n et retourne une tableau contenant les nombres premiers inférieurs à n. Par exemple si n vaut 10, le tableau retourné doit contenir les entiers 2, 3, 5, 7. Cette méthode doit appeler la méthode premier de l’exercice précédent.

Comme le nombre de nombre premiers n’est pas connu à l’avance, la méthode commence par les stocker dans un tableau de taille suffisante (à déterminer), qui sera ensuite recopié dans un tableau ayant exactement la taille nécessaire.

"Indice

public static int[] premiers(int n)
{
    int[] t = new int[n/2 + 1];
    int nbPremEnr = 0; // Nombre de nombres premiers enregistrés

    for(int candidat=2; candidat<n; candidat++)
    {
        // À compléter
    }

    int[] r = new int[nbPremEnr];
    // À compléter

    return r;
}

"Indice

public static int[] premiers(int n)
{
    int[] t = new int[n/2 + 1];
    int nbPremEnr = 0;

    for(int candidat=2; candidat<n; candidat++)
    {
        if(premier(candidat))
        {
            // À compléter
        }
    }

    int[] r = new int[nbPremEnr];
    for(int i=0; i<nbPremEnr; i++)
    {
        // À compléter
    }

    return r;
}

"Solution"

public static int[] premiers(int n)
{
    int[] t = new int[n/2 + 1];
    int nbPremEnr = 0;

    for(int candidat=2; candidat<n; candidat++)
    {
        if(premier(candidat))
        {
            t[nbPremEnr] = candidat; nbPremEnr++;
        }
    }

    int[] r = new int[nbPremEnr];
    for(int i=0; i<nbPremEnr; i++)
    {
        r[i] = t[i];
    }

    return r;
}

A-ass-10

Vous devez réaliser une méthode acceptant en paramètre un entier n et retournant une chaîne de caractères constituée de n lettres majuscules tirées aléatoirement. Les informations suivantes vous seront utiles :

La méthode de classe prédéfinie Math.ramdom() retourne une nombre aléatoire de type double compris entre 0.0 (inclus) et 1.0 (exclus).
Si s est une chaîne de caractères, c’est à dire un objet de type String, et si i est un entier, alors s.charAt(i) retourne le caractère situé en position i dans s.
Si c est un caractère et s est une chaîne, alors s+c est la chaîne obtenue en ajoutant de caractère c à la fin de s.

"Indice

public static String ramdomStr(int n)
{
    String lettres = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
    String r = "";

    for(int i=0; i<n; i++)
    {
        // À compléter.
    }

    return r;
}

"Indice

public static String ramdomStr(int n)
{
    String lettres = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
    String r = "";

    for(int i=0; i<n; i++)
    {
        int pos = (int)(lettres.length() * Math.random());
        // À compléter
    }

    return r;
}

"Solution"

public static String ramdomStr(int n)
{
    String lettres = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
    String r = "";

    for(int i=0; i<n; i++)
    {
        int pos = (int)(lettres.length() * Math.random());
        r = r + lettres.charAt(pos);
    }

    return r;
}

A-ass-11

Vous devez réaliser une méthode acceptant en paramètre une chaîne s et retournant la chaîne de caractères obtenue en remplaçant chaque lettre minuscule par une lettre majuscule avec une probabilité 1/2.

Par exemple, l’appel…

System.out.println(effect("Bonjour, Comment allez-vous ?"));

…peut afficher des chaines telles que :

BoNJOUR, CoMMeNT ALLez-vOus ?
BOnJour, COmMeNt aLLEz-VouS ?
BonJoUR, CoMmeNt alleZ-VoUs ?

L’information suivante vous sera utile : si c est un caractère représentant une lettre minuscule, alors Character.toUpperCase(c) retourne la lettre majuscule correspondante. Dans le cas où c ne représente pas une lettre majuscule, l’appel retourne c.

"indice"

    public static String effect(String s)
    {
        String r = "";

        for(int i=0; i<s.length(); i++)
        {
            if(Math.random() > 0.5)
            {
                // À compléter
            }
            else
            {
                // À compléter
            }
        }
        return r;
    }
}

"Solution"

    public static String effect(String s)
    {
        String r = "";
        for(int i=0; i<s.length(); i++)
        {
            if(Math.random() > 0.5)
            {
                r = r + s.charAt(i);
            }
            else
            {
                r = r + Character.toUpperCase(s.charAt(i));
            }
        }
        return r;
    }
}

Exercices d’approfondissement

Ne traitez ces exercices que si vous avez traité et maitrisé les exercices de découverte et d’assimilation de toutes les parties déjà en ligne.

A-top-00

Vous devez réaliser une méthode de classe premiers qui accepte en paramètre un entier n et retourne une tableau contenant les nombres premiers inférieurs à n. Par exemple si n vaut 10, le tableau retourné doit contenir les entiers 2, 3, 5, 7. Mais cette méthode doit être plus efficace que celle demandée dans un des exercices d’assimilation de cette partie. Pour déterminer si un nombre $x$ est composé ou premier, elle doit tester sa divisibilité par les nombres premiers compris entre 2 et $\lfloor \sqrt x \rfloor$, qui ont déjà été préalablement stockés dans le tableau, et uniquement par ces entiers. En effet, tout nombre composé est divisible par au moins un nombre premier compris entre 2 et $\lfloor \sqrt x \rfloor$. La preuve est laissée à la discrétion du lecteur, si affinité.

A-top-01

Le principe est simple, mais le codage nécessite d’être très attentifs et rigoureux. Imaginons qu’on cherche les nombres premiers inférieur à 100. On crée un tableau de 100 Booléens, dont les indices des cellules vont de 0 à 99. Les cellules sont initialisées à false. On place truedans les cellules d’indices 0 et 1, puis dans toutes les cellules d’indices pairs sauf 2, dans toutes les cellules d’indices multiples de 3 sauf 3 , multiples de 5 sauf 5, multiples de 7 sauf 7, etc. Pour faire cela, on utilise uniquement des boucles et des additions, donc ni division, ni modulo, ni multiplications. Par exemple pour les multiples de 3, on place true dans les cellules d’indices 3+3, 3+3+3, 3+3+3+3, etc. À l’issue de ce remplissage, les indices des cellules contenant falsesont les nombres premiers recherchés.

La figure suivante illustre les deux premières étapes du remplissage.

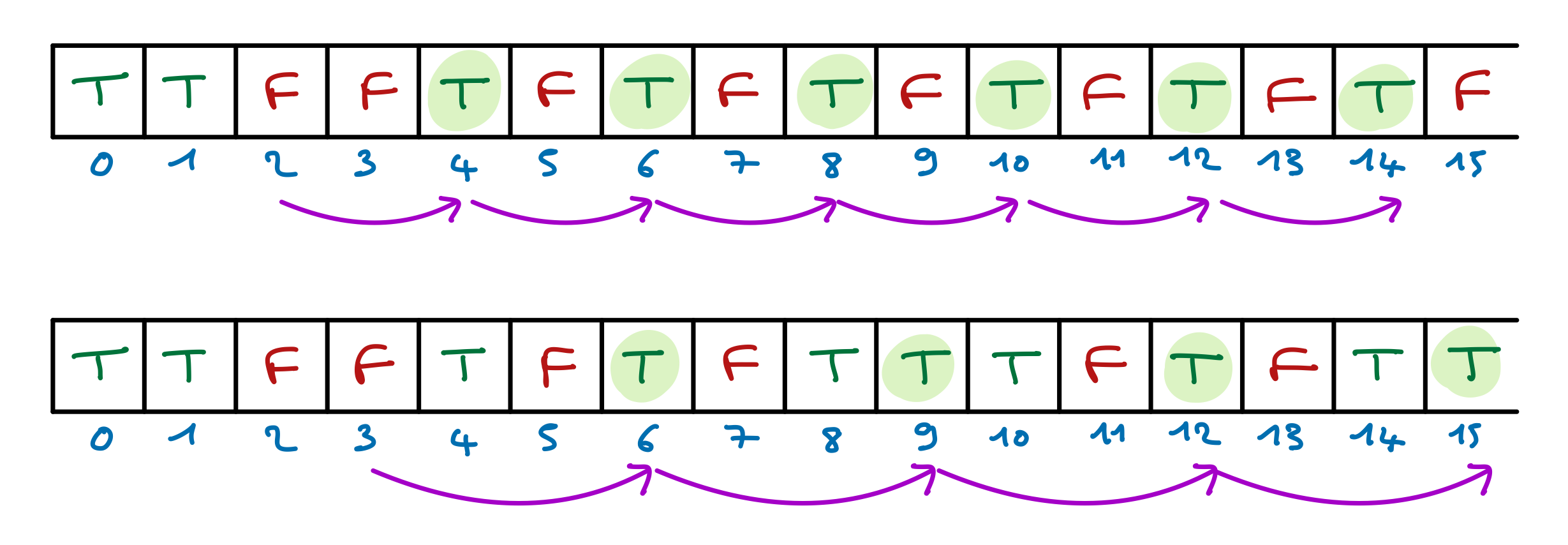
Cette méthode est très connue, donc vous pourrez facilement trouver des explications supplémentaire sur le WEB. Mais attention, vous pourrez aussi trouver des algorithmes détaillés et même des programmes déjà réalisés. Recopier ces codes ferait perdre tout intérêt à cet exercice dont le but est de développer votre pensée algorithmique.

Le tableau retourné devra contenir la liste des nombres premiers recherchés, exactement comme pour l’exercice précédents. Le tableau ayant permis de réaliser le crible est juste un tableau intermédiaire utilisé par la méthode et n’est pas le tableau à retourner.