Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.

Partie A

A1 (1 point)

Donnez les solutions, si applicable, du réseau de contraintes suivant :

Variables : \(A\) de domaine \(\{1,2,3\}\), \(B\) de domaine \(\{4,5,6\}\), \(D\) de domaine \(\{7,8,9\}\), \(C\) de domaine \(\{10,11,12\}\).

Contraintes :

• \(q_1\) sur \(A,B\) : \(\{(1,4),(2,6),(3,5)\}\)
• \(q_2\) sur \(B,C\) : \(\{(4,11),(5,10)\}\)
• \(q_3\) sur \(C,D\) : \(\{(10,8),(11,9),(12,9)\}\)
• \(q_4\) sur \(A,D\) : \(\{(1,9),(2,7),(3,9)\}\)

A2 (1 point)

Donnez la représentation en extension de le contrainte logique \(C = A \vee B\) (où, bien évidemment, les variables ont toutes le domaine \(\{0,1\}\)).

Partie B

Soit un entier positif \(N\). Soit une variable \(X\) ayant pour domaine \(1..N\). Soit les variables Booléennes \(X_1,…,X_N\) . On appelle représentation unaire d’une assignation \(X=x\) l’assignation de \(X_1,…,X_N\) telle que :

• \(X_x = 1\),
• pour tout \(y\in 1..N, y\neq x\), \(X_y = 0\).

Par exemple, pour \(N=3\), la représentation unaire de l’assignation \(X=2\) est \(X_1=0, X_2=1, X_3=0\).

---

Soit la variable \(X\) de domaine \(\{1,2,3\}\) et les variables \(X_1, X_2, X_3\) de domaines \(\{0,1\}\). On souhaite spécifier une ensemble \(Q\) de contraintes appelées contraintes de liaison (chanelling constraints en anglais) qui assure que toute assignation de \(X, X_1, X_2, X_3\) satisfait toutes les contraintes de \(Q\) si et seulement si les valeurs de \(X_1, X_2, X_3\) constituent la représentation unaire de la valeur de \(X\).

B1 (1 point)

Donnez une spécification de \(Q\) en extension. Une seule contrainte est suffisante, donc on a \(Q=\{q\}\) où \(q\) est une contrainte sur \(X, X_1, X_2, X_3\).

B2 (2 points)

Donnez une spécification de \(Q\) en compréhension avec des contraintes arithmétiques. Une solution est possibles avec 2 contraintes.

B3 (1 point)

Donnez une spécification de \(Q\) en compréhension dans le cas général d’une contrainte de liaison entre une variable \(X\) et les variables Booléennes \(X_1,…,X_N\), où \(N\) est un entier positif quelconque.

Partie C

Pour chacune des questions, vous devez répondre en donnant, dans un ordre plausible, les valeurs retirées lors de la restauration de la cohérence de domaines du réseau de contraintes ou de la contrainte donnée dans l’énoncé. Aucune justification n’est demandée. Vous devez juste donner la liste des valeurs retirées en utilisant la notation \(V\neq x\) pour dire que la valeur \(x\) est retirée du domaine de \(V\).

C1 (1 point)

Restaurez la cohérence de domaine de la contrainte \(\text{alldiff}(A, B, C, D, E, F)\) dont les variables ayant respectivement pour domaines \(\{1, 2, 4\}\), \(\{1, 3, 5\}\), \(\{2,3,6\}\), \(\{4,5\}\), \(\{4,6\}\), \(\{5,6\}\).

C2 (1,5 point)

Restaurez la cohérence de domaine du réseau de contraintes suivant :

• Variables : \(A, B, C\) ayant toutes pour domaine \(\{1,2,3\}\).
• Contraintes :
  • \(q_1\) : \(A + 2B + 3C = 12\).
  • \(q_2\) : \(A + 2B + 2C = 10\).

C3 (1,5 point)

Restaurez la cohérence de domaine du réseau suivant :

Variables : \(A,B,C,D\) ayant toutes pour domaine \(\{1,2,3\}\).

Contraintes :

• \(q_1\) sur \(A,B\) : \(\{(3,3),(2,1),(1,2)\}\)
• \(q_2\) sur \(B,C\) : \(\{(3,3),(2,1),(1,1)\}\)
• \(q_3\) sur \(C,D\) : \(\{(1,2),(2,1),(3,3)\}\)
• \(q_4\) sur \(A,D\) : \(\{(1,1,(2,2),(3,3)\}\)

Partie D

D1 (2 points)

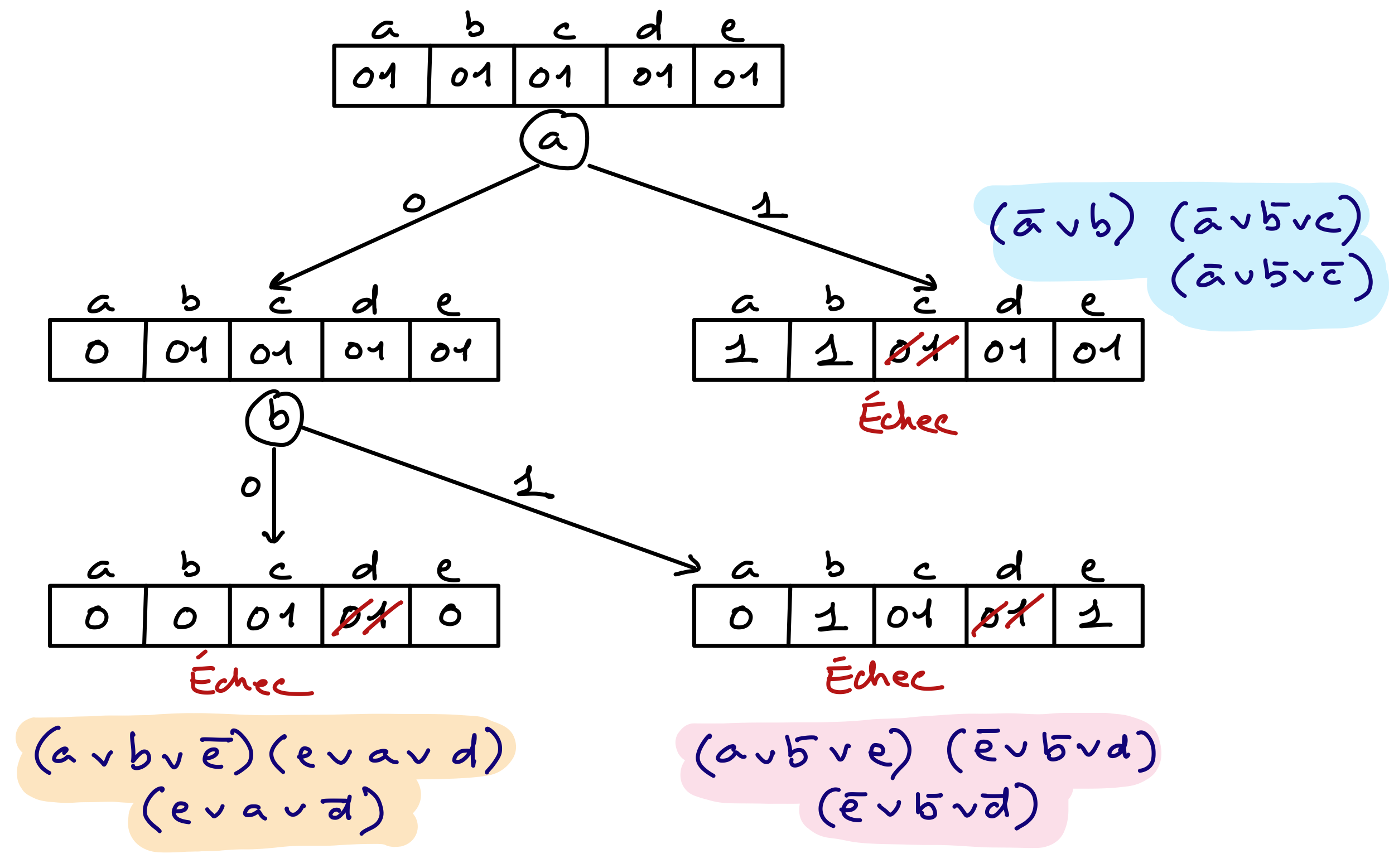
Soit le réseau de contraintes suivant dont les variables ont pour domaines {0,1} (représentant les valeurs vrai et faux) :

\((\neg a \vee b)\), \((\neg a \vee \neg b \vee c)\), \((\neg a \vee \neg b \vee \neg c)\), \((a \vee b \vee \neg e)\), \((e \vee a \vee d)\), \((e \vee a \vee \neg d)\), \((a \vee \neg b \vee e)\), \((\neg e \vee \neg b \vee d)\), \((\neg e \vee \neg b \vee \neg d)\).

Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Vous devez utiliser \(a\) comme première variable de branchement. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.