Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.
Partie A
A1 (1 point)
Donnez les solutions, si applicable, du réseau de contraintes suivant :
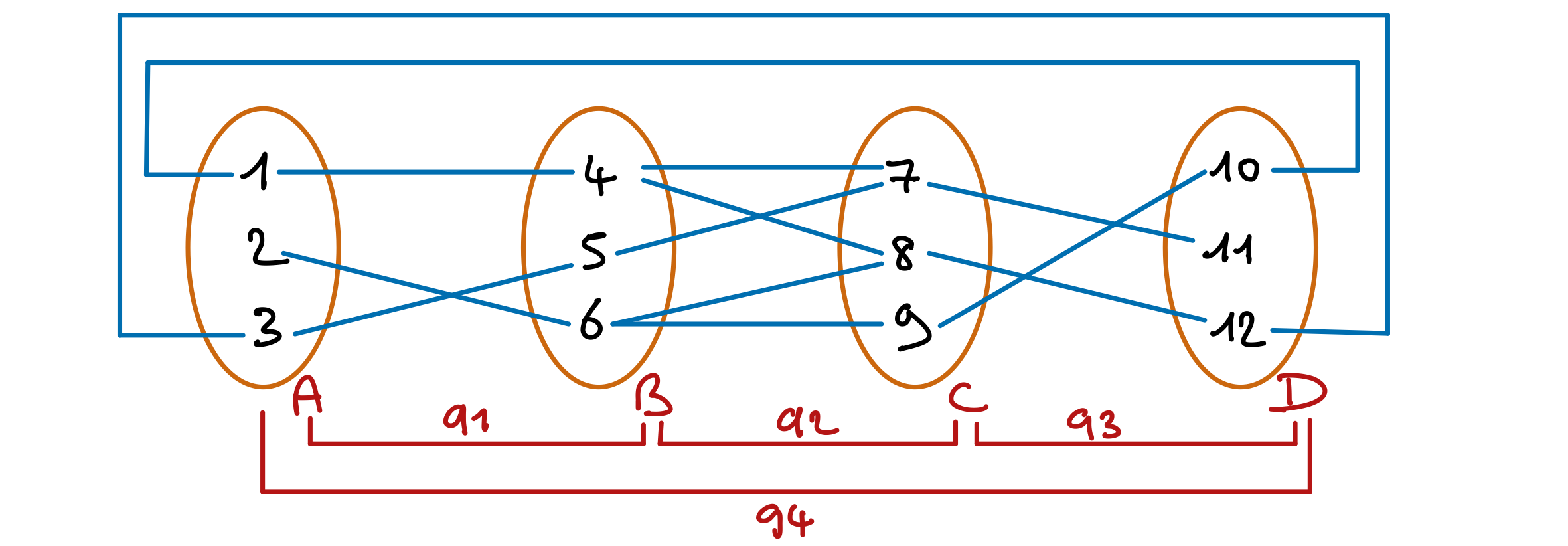
Aucune solution.
A2 (1 point)
Soient les variables A, B, C de domaines respectifs {1,2}, {2,3} et {3,4}. Soient les contraintes suivantes :
- q1 sur A, B : {(1,2), (2,3)}.
- q2 sur B, C : {(2,4)}.
- q : q1 ou q2 (la contrainte satisfaite par et seulement par les assignations de A, B, C qui satisfont q1 ou q2).
Donnez la représentation en extension de q.
Sur \(A,B,C\) : \(\{(1,2,3),(1,2,4),(2,3,3),(2,3,4),(2,2,4)\}\).
Partie B
B1 (1 point)
On veut placer \(k\) personnes sur un coté d’une table rectangulaire disposant de \(k\) places. On attribue, par commodité, un numéro compris entre \(1\) et \(k\) à chaque place et on fait de même pour chaque personne à placer.
Chaque personne \(i\) peut exclure certaines autres personnes, c’est à dire refuser que ces autres personnes (si applicable) soient placées à coté de lui. Les personnes exclues par une personne \(x\) sont données par un ensemble \(E_x\). Voici un exemple avec \(k=4\) :
\[E_1=\{2,3\}, E_2=\{1\}, E_3=\{1,4\}, E_4=\{3\}
\]
- La personne 1 exclut les personnes 2 et 3,
- la personne 2 exclut la personne 1,
- la personne 3 exclut les personnes 1 et 4,
- la personne 4 exclut la personne 3.
Voici une solution permettant de placer les 4 personnes en respectent leurs incompatibilités.
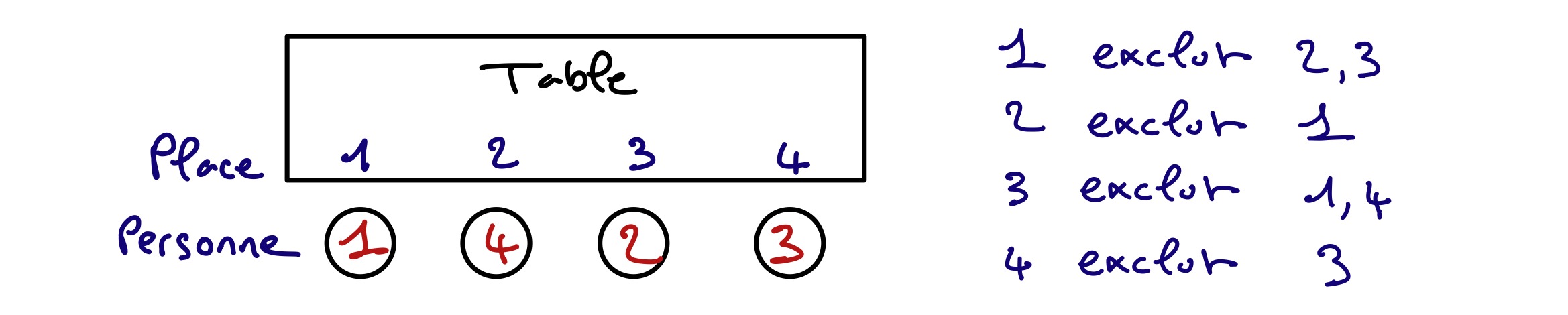
Proposez une modélisation en extension de l’exemple ci-dessus en utilisant les variables, domaines et contraintes qui vous paraissent les plus pertinentes.
Une variable par place : \(P_1, P_2, P_3, P_4\) de domaine \(\{1,2,3,4\}\). \(P_i=j\) signifie que la personne \(j\) occupe la place \(i\).
Contraintes de compatibilité :
- Sur \(P_1, P_2\) : \(\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}\).
- Sur \(P_2, P_3\) : \(\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}\).
- Sur \(P_3, P_4\) : \(\{(1,4), (4,1), (2,3), (2,4), (3,2), (4,2)\}\).
Contraintes de différence (pour que chaque place soit occupée par une personne différente) :
- Sur \(P_1, P_3\) : \(\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}\).
- Sur \(P_1, P_4\) : \(\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}\).
- Sur \(P_2, P_4\) : \(\{(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)\}\).
B2 (3 points)
On revient au cas général où on a \(k\) personnes à placer. On souhaite modéliser le problème à l’aide de variables Booléennes \(P_{ix}\), pour \(i\) et \(x\) compris entre 1 et \(k\), avec la convention suivante : \(P_{ix}=1\) signifie que la place \(i\) est occupée par la personne \(x\).
Donnez une spécification en compréhension de toutes les contraintes nécessaires, les données du problèmes étant les ensembles \(E_1\) à \(E_k\). Vous pouvez utiliser des contraintes arithmétiques et / ou logiques.
Chaque place est occupée par une personne, chaque personne occupe exactement une place :
\(\forall i \in 1..k, \sum_{x=1}^k P_{i,x} = 1\), \(\forall x \in 1..k, \sum_{i=1}^k P_{i,x} = 1\).
Incompatibilités :
\(\forall i\in 1..k-1, \forall x\in 1..k, \forall y\in E_x, \neg(P_{i,x}\wedge P_{i+1,y})\)
\(\forall i\in 1..k-1, \forall x\in 1..k, \forall y\in E_x, \neg(P_{i+1,x}\wedge P_{i,y})\)
Partie C
Pour chacune des questions, vous devez répondre en donnant, dans un ordre plausible, les valeurs retirées lors de la restauration de la cohérence de domaines du réseau de contraintes ou de la contrainte donnée dans l’énoncé. Aucune justification n’est demandée. Vous devez juste donner la liste des valeurs retirées en utilisant la notation \(V\neq x\) pour dire que la valeur \(x\) est retirée du domaine de \(V\).
C1 (1 point)
Restaurez la cohérence de domaine de la contrainte \(\text{alldiff}(A, B, C, D, E)\) dont les variables ont les domaines suivants :
\(A, B\) : \(\{1, 2, 3\}\), \(C\) : \(\{1, 2, 3, 4\}\), \(D\) : \(\{4,2\}\), \(E\) : \(\{4,3\}\).
\(D\neq 4\), \(A\neq 2\), \(B\neq 2\), \(C\neq 2\), \(E\neq 4\), \(E\neq 3\), incohérence globale.
C2 (2 points)
Restaurez la cohérence de domaine du réseau de contraintes suivant :
- Variables : \(A\) de domaine \(\{1,2\}\), \(B\) de domaine \(\{4,5\}\), \(C\) de domaine \(\{4,5\}\), \(X\) de domaine \(\{1,2,3\}\), \(Y\) de domaine \(\{1,2,3\}\).
- Contraintes :
- Sur \(A, B, C\) : \(\{(1,4,5), (1,5,4), (2,5,5)\}\).
- Sur \(B, X\) : \(\{(4,1), (4,2), (5,3)\}\).
- Sur \(C, Y\) : \(\{(4,3), (5,2)\}\).
- Sur \(X,Y\) : \(\{(1,2), (2,3), (3,1)\}\).
\(Y\neq 1, X\neq 3, B\neq 5, A\neq 2, C\neq 4, Y\neq 3, X\neq 2\)
Le filtrage peut être plus facile en s’appuyant sur une représentation graphique telle que celles-ci :
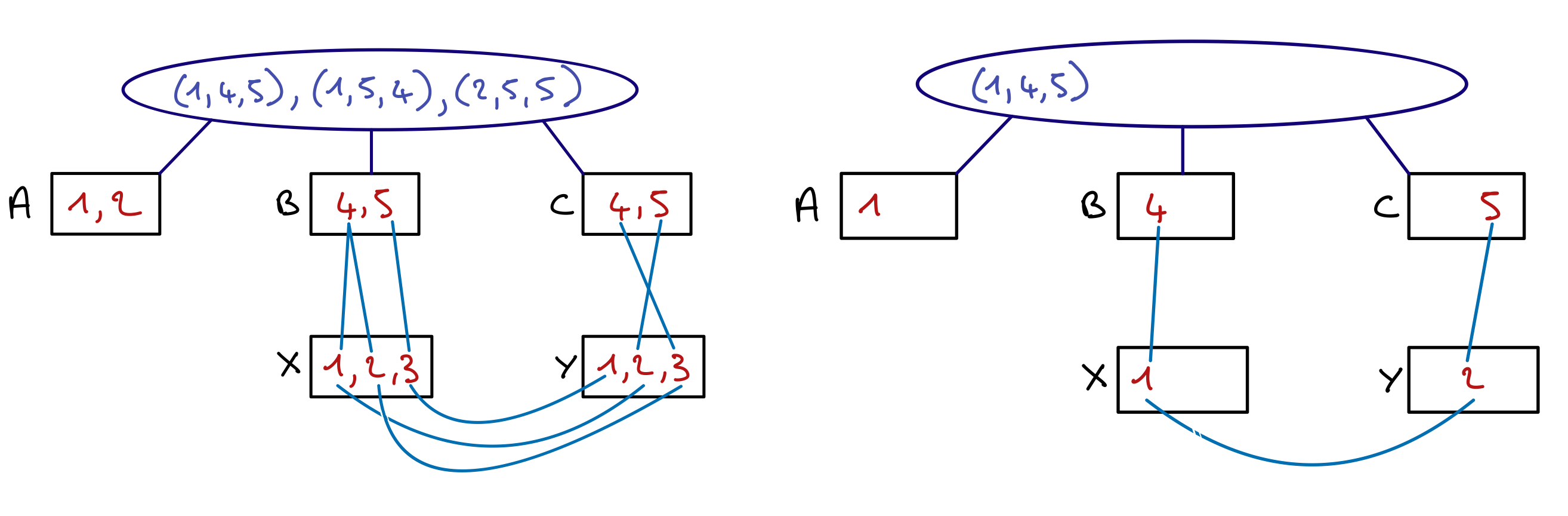
C3 (1 point)
Restaurez la cohérence de domaine de la contrainte \(9 X_2 + 3 X_1 + X_0 = Y\) dont les variables ont les domaines suivants :
\(X_0, X_1, X_2\) : \(\{0,1,2\}\), \(Y\) : \(\{10,13,16\}\).
\(X_2\neq 0, X_2\neq 2, X_0\neq 0, X_0 \neq 2\)
Partie D
D1 (2 points)
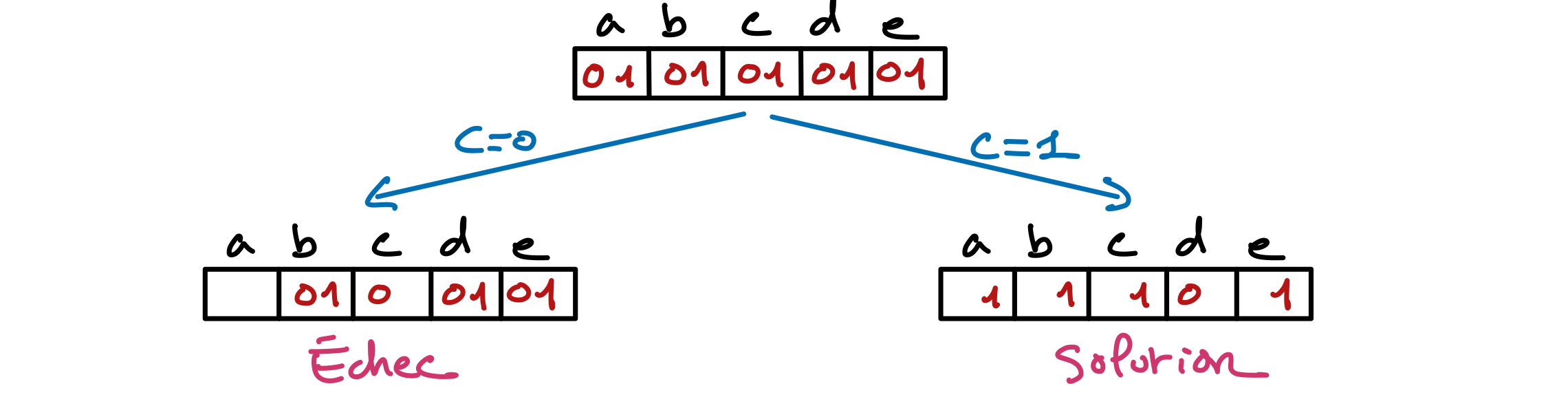
Soit le réseau de contraintes suivant dont les variables ont pour domaines {0,1} (représentant les valeurs vrai et faux) :
\((a \vee \neg b), (a \vee c), (b \vee \neg c), (\neg a \vee c), (\neg c \vee \neg d), (\neg a \vee \neg b \vee \neg c \vee d \vee e)\).
Donnez l’arbre de recherche illustrant le déroulement de l’algorithme MAC sur ce réseau de contraintes. Choisissez les variables de branchement qui vous paraissent être pertinentes pour minimiser l’arbre de recherche. Précisez à chaque nœud les domaines des variables en barrant celles qui sont filtrées.