Documents autorisés : une feuille A4 recto-verso pour chacune de parties A, B, C, D, manuscrite ou imprimée.
Partie A
A1 (1 point)
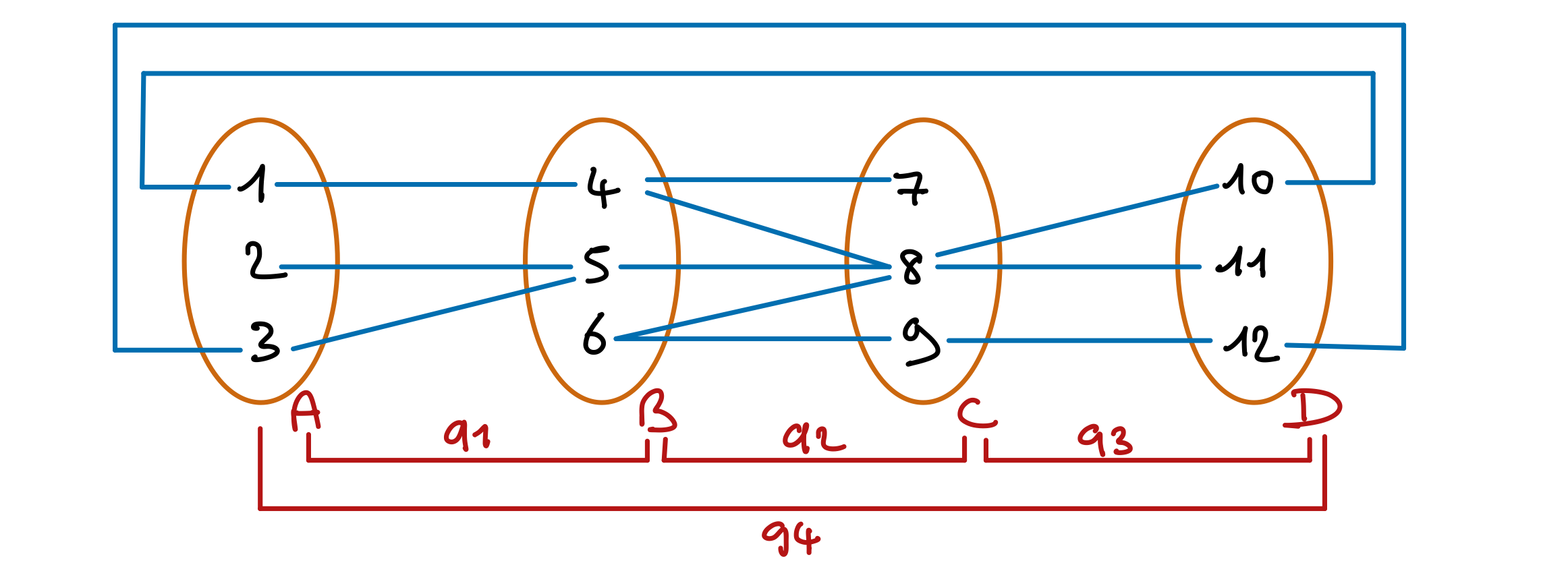
Donnez les solutions, si applicable, du réseau de contraintes suivant :
A2 (1 point)
Une solution : \(A=1, B=4, C=8, D=10\).
Soient les variables A, B, C de domaines respectifs {1,2}, {2,3} et {3,4}. Soient les contraintes suivantes :
- q1 : A < B.
- q2 : B < C.
- q : q1 et q2 (la contrainte satisfaite par et seulement par les assignations de A, B, C qui satisfont q1 et q2).
Donnez les représentations en extension de q1, q2 et q.
- \(q_1\) : sur \(A,B\), \(\{(1,2),(1,3),(2,3)\}\).
- \(q_2\) : sur \(B,C\), \(\{(2,3),(2,4),(3,4)\}\).
- \(q\) : sur \(A,B,C\), \(\{(1,2,3),(1,2,4),(1,3,4),(2,3,4)\}\).
Partie B
Soit \(N\) un entier au mois égal à 3 et \(A_1,…,A_N\), \(B_1,…,B_N\) des variables Booléennes, i.e., ayant pour domaine \(\{0,1\}\).
Toute assignation complète des variables \(A_1,…,A_N\) représentent le positionnement d’une tâche \(A\) dont l’heure de début est la plus petite valeur \(i\) telle que \(A_i=1\) et la durée est le nombre de valeurs de consécutives assignées à 1.
Par exemple, pour \(N=5\) les valeurs autorisées des variables \(A_1\) à \(A_5\) pour représenter de tâche d’une durée de 3 heures sont les suivantes :
11100 // tâche A commence à 0h, durée 3h
01110 // tâche A commence à 1h, durée 3h
00111 // tâche A commence à 2h, durée 3h
Les assignations dans lesquelles un ou plusieurs 0 sont encadrés par des 1, telles que 10110, sont interdites.
La même convention est appliquée aux variables \(B_1,…,B_N\) pour la représentation d’une tâche \(B\).
Pour exprimer mathématiquement que tous les bits à 1 d’une assignation sont consécutifs, on dit qu’il ne peut y avoir de motif 1…01 ni de motif 10…1 dans la séquence.
Ceci correspond aux deux ensembles de contraintes suivants :
- \(\forall i\in 2..N-1, \forall j\in 1..i-1, \neg A_j \vee A_i \vee \neg A_{i+1}\)
- \(\forall i\in 1..N-2, \forall j\in i+2..N, \neg A_i \vee A_{i+1} \vee \neg A_{j}\)
Par exemple, l’assignation 10110 falsifie la contrainte \(\neg A_1 \vee A_3 \vee \neg A_4\) qui est une des contraintes mentionnées plus haut.
Les mêmes contraintes sont appliquées aux variables \(B_1,…,B_N\).
B1 (1 point)
Soient \(K_A\) et \(K_B\) deux entiers. On suppose que \(K_A+K_B\leq N\). Donnez une spécification en compréhension (sur les variables \(A_1,…,A_N\), \(B_1,…,B_N\)) des contraintes qui expriment les propriétés suivantes :
- La durée de la tâche \(A\) est \(K_A\),
- La durée de la tâche \(B\) est \(K_B\).
- \(\sum_{i=1}^N A_i = K_A\).
- \(\sum_{i=1}^N B_i = K_B\).
B2 (1 point)
Donnez une spécification en extension de la contrainte qui exprime que la tâche \(A\) dure 2 heures, pour \(N=5\).
Sur \(A_1,A_2,A_3, A_4,A_5\) : \(\{(1,1,0,0,0),(0,1,1,0,0),(0,0,1,1,0),(0,0,0,1,1)\}\).
B3 (2 points)
Donnez la spécification en compréhension les contraintes supplémentaires (sur les variables \(A_1,…,A_N\), \(B_1,…,B_N\)) qui permettent de dire que la tâche \(A\) doit être complètement réalisée lorsque la tâche \(B\) commence.
Vous devez utiliser des contraintes logiques (basées sur \(\neg, \vee, \wedge\)) ou arithmétiques linéaires (basées sur -, +, <, >, =, etc.) ou des compositions logiques de contraintes arithmétiques.
Voici un exemple d’assignations avec \(N=10\) et \(K=3\) qui satisfont les contraintes supplémentaires que vous devez spécifier.
0011100000 // tâche A
0000001110 // tâche B
Et trois exemples qui doivent falsifier au moins une de ces contraintes.
0011110000 // tâche A
0000111100 // tâche B
0011100000 // tâche A
0111000000 // tâche B
0000011000 // tâche A
0110000000 // tâche B
\(\forall i \in 1..N\), \(\forall j\in 1..i\), \(\neg(A_i \wedge B_j)\).
D’autres solutions existent.
Partie C
C1 (4 points)
Voici le réseau de contrainte qui modélise le problème de l’existence d’une règle de Golomb de longueur 6 à 4 graduations.
Variables :
- \(G_0\) de domaine \(\{0\}\), \(G_3\) de domaine \(\{6\}\),
- \(G_1, G_2\) de domaine \(\{1,2,3,4,5\}\)
- \(D_0, D_1, D_2, D_3, D_4, D_5\) de domaine \(\{1,2,3,4,5,6\}\).
Contraintes :
- \(G_0 < G_1, G_1 < G_2, G_2 < G_3\),
- \(D_0=G_1-G_0\), \(D_1=G_2-G_0\), \(D_2=G_3-G_0\), \(D_3=G_2-G_1\), \(D_4=G_3-G_1\), \(D_5=G_3-G_2\),
- AllDiff\((D_0, D_1, D_2, D_3, D_4, D_5)\)
Voici une représentation graphique de ce réseau de contraintes :
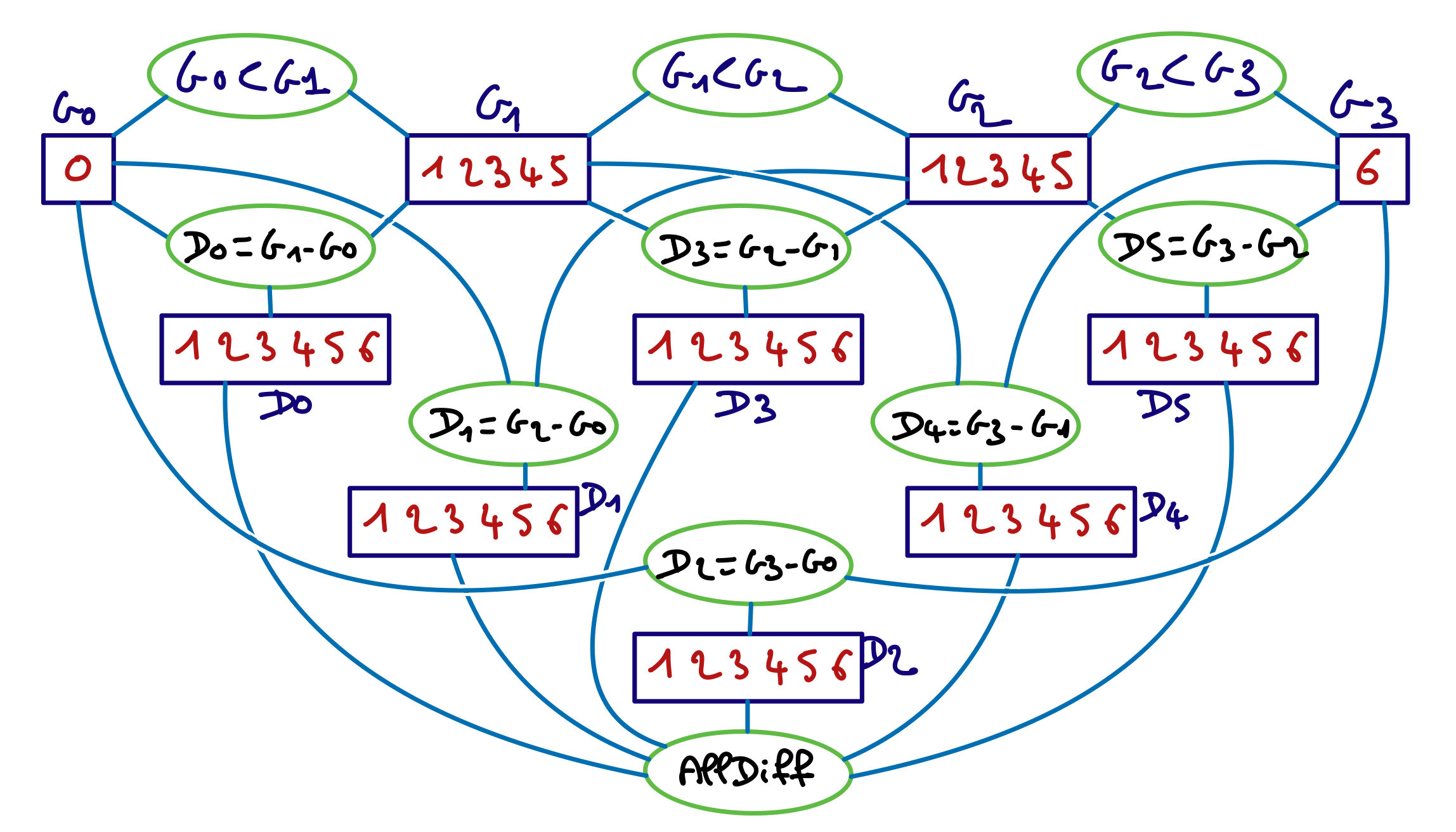
Restaurez la cohérence de domaine de ce réseau de contrainte. Donnez les valeurs retirées dans un ordre cohérent avec le principe de filtrage. Utilisez la notation \(V\neq x\) pour indiquer que la valeur \(x\) est retirée du domaine de la variable \(V\).
Par exemple, vous pouvez commencer par \(D_2 \neq 1\) car la valeur \(D_2=1\) n’a pas de support pour la contrainte \(D_2=G_3-G_0\). Mais il existe plusieurs séquences correctes.
\(G_1\neq 5, G_2\neq 1, D_0\neq 5, D_0\neq 6, D_3\neq 5, D_3\neq 6,\)
\(D_5\neq 5, D_5\neq 6, D_1\neq 1, D_1\neq 6, D_4\neq 1, D_4\neq 6,\)
\(D_2\neq 1, D_2\neq 2, D_2\neq 3, D_2\neq 4, D_2\neq 5.\)
Partie D
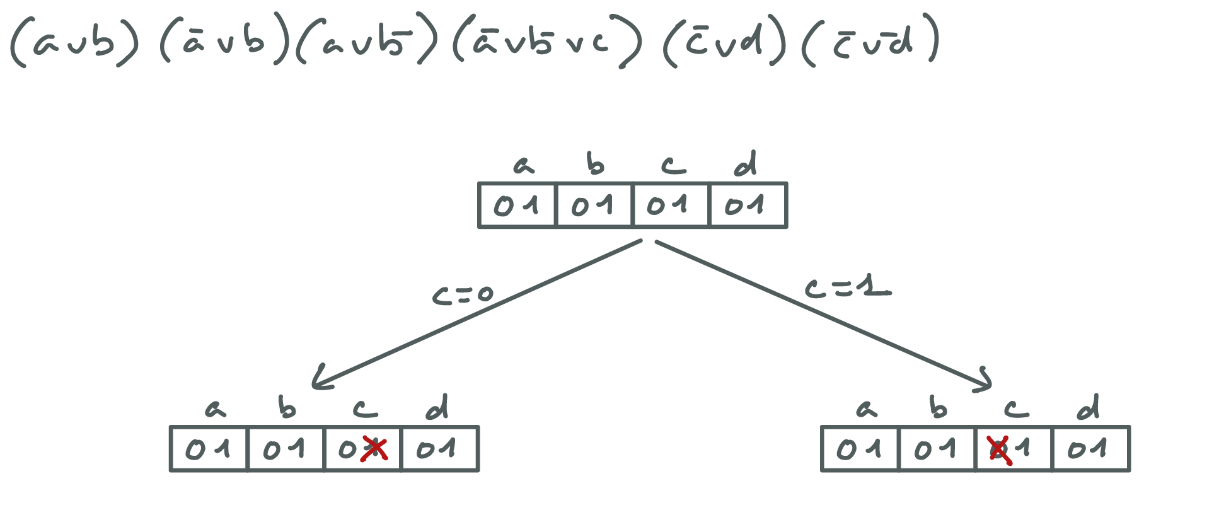
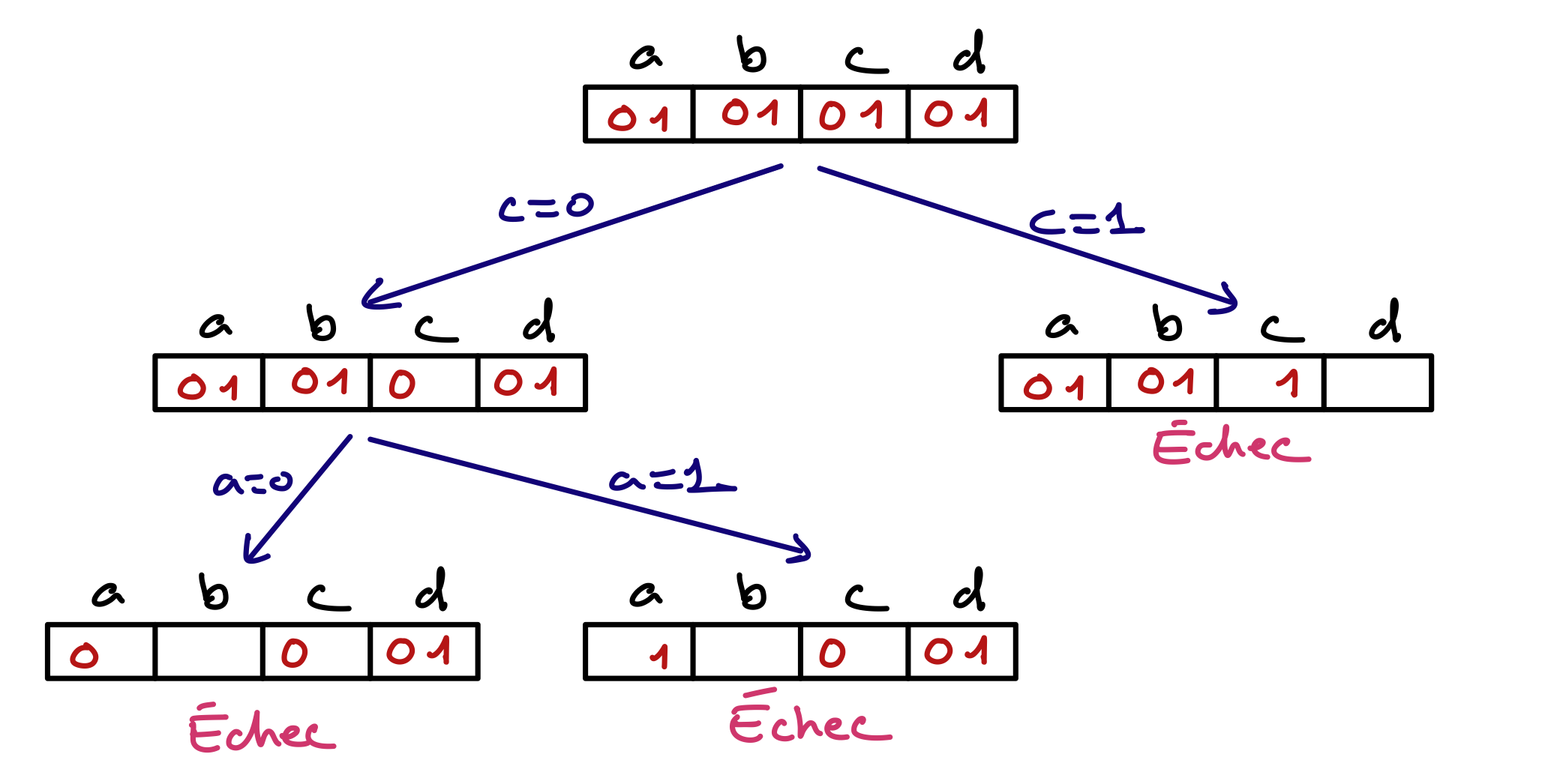
D1 (2 points)
Voici un réseau de 6 contraintes logiques et le début de l’arbre de recherche de l’algorithme MAC sur ce réseau. Vous devez compléter l’arbre en choisissant au mieux (si applicable) les variables de branchement restantes. A chaque nœud ou feuille, redonnez les domaines en barrant les valeurs éliminées par filtrage ou par assignation de la variable de branchement. A chaque feuille de l’arbre de recherche, précisez s’il y a échec ou solution.