Partie A

A1 (2 point)

Réalisez une méthode de classe…

public static void amplitude(int[] tab)
{
  // À compléter
}

…qui retourne la différence entre la plus grande et la plus petite valeur du tableau tab. Par exemple si tab contient les valeurs 5, 1, 4, 23, 4 ,4, 8, 5, alors la valeur de retour devra être 22 c’est à dire 23-1.

public static int amplitude(int[] tab)
{
    int mini = tab[0]; int maxi = tab[0];
    for(int i=1; i<tab.length; i++)
    {
        if(tab[i] > maxi) maxi = tab[i];
        else if(tab[i] < mini) mini = tab[i];
    }
    return  maxi - mini;
}

A2 (1 point)

Réalisez une méthode main qui crée un tableau d’entier contenant les valeurs de l’exemple précédent, qui appelle la méthode amplitude avec ce tableau et affiche le résultat.

public static void main(String[] args)
{
    int[] tab = {5, 1, 4, 23, 4, 4, 8, 5};
    System.out.println(amplitude(tab));
}

Partie B

Soit une classe Terrain représentant un terrain agricole de forme rectangulaire localisé par les coordonnées géographiques (qui sont des valeurs de types double, en mètres) de deux de ses coins opposés. A cette fin, la classe Terrain a 4 attributs privés de type double nommés x1, y1, x2, y2. Elle possède en outre un attribut privé nom de type String qui permet d’attribuer un nom à chaque terrain.

La classe Terrain dispose d’un constructeur Terrain(double x1, double y1, double x2, double y2, String nom) permettant la création d’une instance à l’aide des informations fournies en paramètres. Elle dispose également d’une méthode toString retournant une description textuelle du terrain courant. On supposera que x1 < x2 et y1 < y2.

public class Terrain
{
    private String nom;
    private double x1; private double y1;
    private double x2; private double y2;

    public Terrain(String nom, double x1, double y1, double x2, double y2)
    {
        this.nom = nom;
        this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2;
    }

    public String toString()

    {
        return "Terrain : " + nom + "(" + x1 + "," + y1 + ") (" + x2 + "," + y2 +")";
    }
}

Soit une classe Cadastre représentant une liste de plusieurs terrains. Nous appellerons cadastre toute instance de cette classe. Cette classe a un attribut privé terrains de type ArrayList<Terrain> qui permet le stockage de toutes les instances de Terrain du cadastre courant.

B1 (1 point)

Donnez la définition du constructeur de la classe Cadastre.

public Cadastre()
{
    this.terrains = new ArrayList<>();
}

B2 (1 point)

Donnez la définition d’une méthode d’instance public void add(double x1, double y1, double x2, double y2, String nom) de la classe Cadastre qui ajoute un nouveau terrain à la liste.

public void add(double x1, double y1, double x2, double y2, String nom)
{
    terrains.add(new Terrain(nom, x1, y1, x2, y2));
}

B3 (1 point)

On suppose que la classe Terrain a une méthode d’instance public double surface() qui retourne la surface du terrain courant.

Donnez la définition d’une méthode d’instance public double surface() de la classe Cadastre qui retourne la somme des surfaces des terrains du cadastre courant.

public double surface()
{
    double r = 0.0;
    for(Terrain t : terrains)
    {
        r = r + t.surface();
    }
    return r;
}

B4 (1point)

Donnez les lignes de codes, supposées être dans une méthode de classe void test() située dans une classe Test, permettant de créer un cadastre, d’y ajouter deux terrains, et d’afficher la surface cumulée des terrains du cadastre.

Cadastre cad = new Cadastre();
cad.add(100,200,120,230,"parcelle 1");
cad.add(560,320,570,330,"parcelle 2");
System.out.println(cad.surface());

Partie C

On considère les classes et interface suivantes.

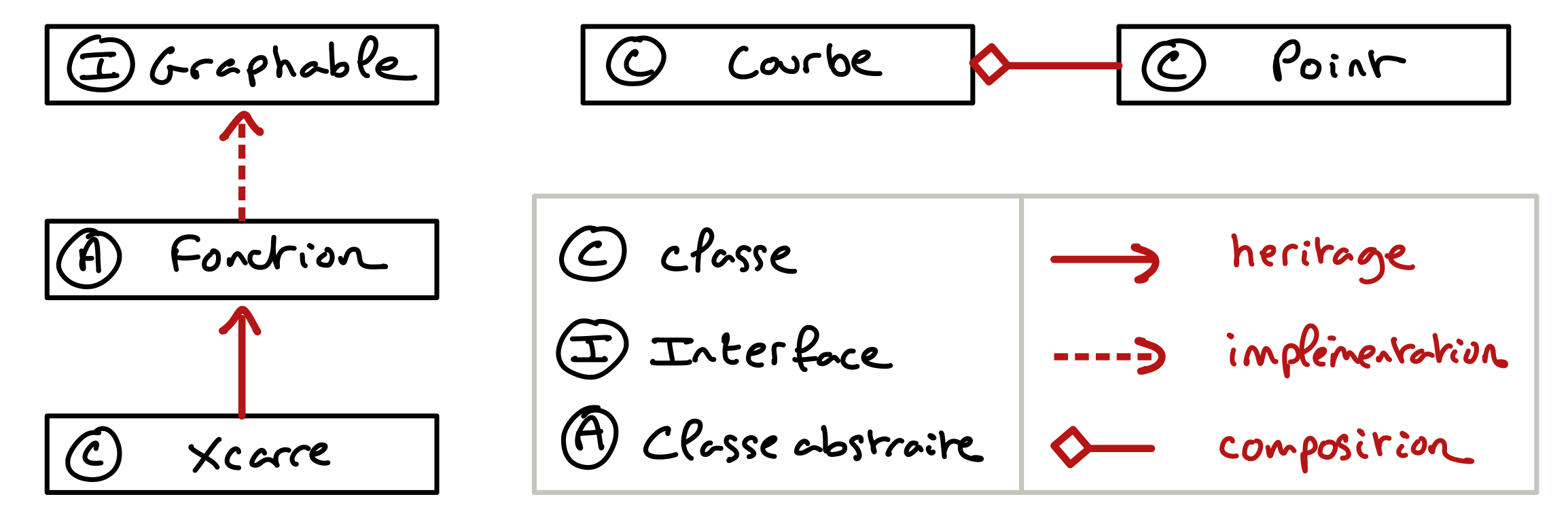
La classe Point représente juste un point avec deux coordonnées de type double.

public class Point
{
    private double x,y;

    public Point(double x, double y) { ... }

    public String toString() { ... }
}

La classe Courbe représente une liste de points pouvant être interprétée comme une courbe si on imagine que chaque point est relié au suivant (si applicable).

public class Courbe
{
    private ArrayList<Point> points;

    public Courbe(){ ... }

    public void add(double x, double y) { ... }

    public String toString() { return }
}

Voici une représentation graphique de l’instance de courbe représentée par la liste de points [(1.0,1.0), (2.0,3.0), (3.0,2.0)].

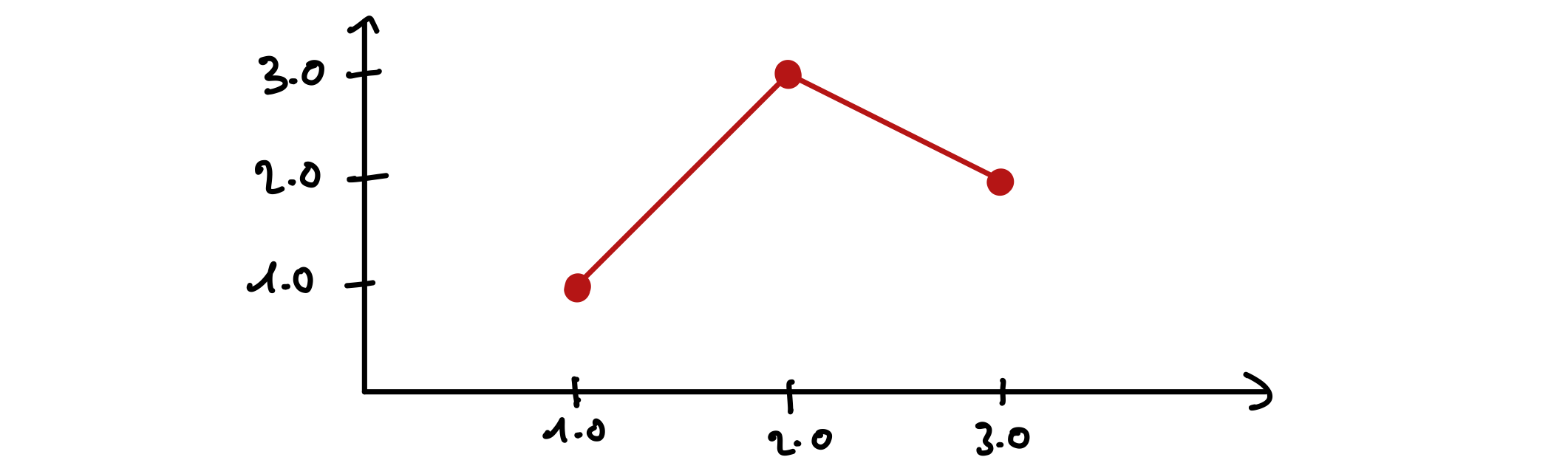
Ceci est juste donné à titre d’exemple. La partie affichage graphique n’est pas du tout traitée dans cet exercice.

L’interface Graphable oblige les classes qui l’implémentent à être dotées d’une méthode permettant de produire une instance de courbe représentée par une liste de n points dont les abscisses (coordonnées \(x\)) vont de min à max avec des écarts constants entre ces abscisses.

Par exemple si n vaut 5, min vaut 10.0 et max vaut 12.0, les abscisses des 5 points devront être 10.0, 10.5, 11.0, 11.5 et 12.0.

public interface Graphable
{
    public Courbe getCourbe(double min, double max, int n);
}

La classe abstraite Fonction représente une fonction calculable. Elle dispose d’une méthode abstraite getImage qui accepte en paramètre une valeur x et retourne l’image de x par cette fonction. Par exemple, dans une classe dérivée de Fonction qui représente la fonction \(x \mapsto x^2\), l’appel getImage(3.0) retournera 9.0.

public abstract class Fonction implements Graphable
{
    public abstract double getImage(double x);

    public Courbe getCourbe(double min, double max, int n)
    {
        // À compléter
    }
}

C1 (2 points)

Implémentez la méthode getCourbe de la classe Foncton.

public Courbe getCourbe(double min, double max, int n)
{
    double delta = (max - min) / (n - 1);
    double x = min;
    Courbe r = new Courbe();
    for(int i = 0; i< n; i++)
    {
        r.add(x, getImage(x));
        x = x + delta;
    }
    return r;
}

C2 (1 point)

Réalisez une classe Xcarre sans attribut, dérivée de Fonction représentant la fonction qui à tout réel \(x\) associe \(x^2\).

public class Xcarre extends Fonction
{
    public double getImage(double x)
    {
        return x * x;
    }
}

C3 (2 points)

On souhaite que la méthode main suivante…

public static void main(String[] args)
{
    Fonction f = new Xcarre();
    System.out.println(f.getNom());
}

…produise l’affichage

Fonction carré

Donnez le code complet de la ou des méthodes concrètes et / ou abstraites à ajouter aux classes Fonction et Xcarre pour obtenir ce résultat sans ajouter d’attribut à ces classses.

public abstract String getNom();

public String getNom()
{
    return "Fonction carré";
}

Partie D

La classe Fraction représente une fraction (un nombre rationnel) ayant un dénominateur et un numérateur.

public class Fraction
{
    private int num;
    private int den;

    public Fraction(int numerateur, int denominateur) throws  DenZero
    {
        if(denominateur == 0) throw new DenZero();
        this.num = numerateur;
        this.den = denominateur;
        normalise();
    }

    public int getDenum() {return den;}

    public int getNum() {return num;}

    public void normalise()
    {
        // Code classifié très secret cosmique
    }

    public Fraction add(Fraction f)
    {
        // À comlpléter
    }

    public String toString()
    {
        return num + " / " + den;
    }
}

Regardez attentivement le code du constructeur. Il lève une exception de type DenZero si par malheur on tente de l’utiliser pour créer une fraction ayant un dénominateur nul. Dans le cas contraire, il initialise les attributs et appelle une méthode de normalisation. Le code de cette méthode est ultra secret et ne sera pas révélé ici. Il permet de normaliser la fraction de manière à ce que le dénominateur soit toujours positif et de la simplifier de manière à minimiser les valeurs du numérateur et du dénominateur. Par exemple, si les valeurs données sont 4 et 12, après simplification au aura 1 / 3.

La classe DenZero est définie ainsi :

public class DenZero extends Exception
{
    public String toString()
    {
        return "Dénominateur nul";
    }
}

D1 (2 points)

Complétez le fonction testFrac suivante de manière à ce qu’elle crée une instance de Fraction représentant la fraction \(a/b\) et affiche sa représentation à l’aide de la méthode toString. Dans le cas où le constructeur de la classe Fraction lève une exception de type DenZero, le message "ERREUR : Dénominateur nul" doit s’afficher.

public static void testFrac(int a, int b)
{
    // À compléter
}

public static void testFrac(int a, int b)
{
    try
    {
        Fraction r = new Fraction(a,b);
        System.out.println(r.toString());
    }
    catch(DenZero e)
    {
        System.out.println("ERREUR  : " + e);
    }
}

D2 (2 points)

On rappelle que la somme de deux fractions valides (avec dénominateurs non nuls) \(a/b\) et \(c/d\) a pour résultat la simplification (avec la méthode normalize) de \((ad + bc) / bd\).

Complétez une méthode add de la classe Fraction en faisant en sorte qu’elle retourne la somme de la fraction courante et de cette désignée par le paramètre f. La fraction courante ne doit pas être modifiée. Si l’exception DenZero est levée lors de la construction du résultat (Ça ne devrait pas se produire, mais il faut le prévoir quand même), la méthode add doit lever une exception de type RuntimeException avec message "Erreur inattendue" passé en argument à son constructeur.

public Fraction add(Fraction f)
{
    // À compléter
}

public Fraction add(Fraction f)
{
    int n = (getNum() * f.getDenum()) + (f.getNum() * getDenum());
    int d = getDenum() * f.getDenum();
    try
    {
        return new Fraction(n, d);
    }
    catch (DenZero e)
    {
        throw new RuntimeException("Erreur inattendue");
    }
}

Partie E

Un multi-ensemble est une structure de donnée pouvant contenir des éléments, comme un ensemble, mais à la différence d’un ensemble, chaque élément peut avoir plusieurs occurrences. Par exemple, {2, 5, 5, 56} est un multi-ensemble dont les éléments sont 2, 5 et 56. L’élément 5 a deux occurrences, alors que les autres en ont une seule.

La classe MultiInt représente un multi-ensemble d’entiers naturels (c’est à dire supérieurs ou égaux à 0).

public class MultiInt
{
    // Attributs à completer

    public MultiInt(int max)
    {
        // À compléter
    }

    public void add(int e)
    {
				// À compléter
    }

    public void remove(int e)
    {
				// À compléter
    }
    // ...
}

La classe MultiInt comporte d’autres méthodes, mais seules celles qui sont mentionnées plus haut nous intéressent dans cet exercices.

Le constructeur permet de créer un multi-ensemble pouvant contenir les éléments compris entre 0 et max, chacun pouvant n’avoir aucune occurrence ou avoir un nombre quelconque d’occurrences.

E1 (4 points)

Vous devez donner le ou les attributs de la classe et le code du constructeur et des deux méthodes. Si e est un entier compris entre 0 et max et m est une instance de MultiInt construite de la manière suivante…

MultiInt m = new MultiInt(max);

…alors :

• m.add(e) ajoute une occurrence de e dans le multi-ensemble désigné par m,
• m.remove(e) retire une occurrence de e s’il en reste au moins une et sinon n’a aucun effet.

Vous devez essayer de trouver une solution permettant de minimiser la complexité en temps (en fonction du nombre d’éléments du multi-ensemble courant) des méthodes add et remove. Vous devez également donner l’ordre de grandeur asymptotique des ces complexité (constante ou logarithmique ou linéaire ou quadratique ou autre …) en justifiant brièvement votre réponse.

public class MultiInt
{
    private int[] tab;

    public MultiInt(int max)
    {
        tab = new int[max+1];
    }

    public void add(int e)
    {
        tab[e]++;
    }

    public void remove(int e)
    {
        if(tab[e]>0) tab[e]--;
    }

    public int count(int e)
    {
        return tab[e];
    }
}