PPC : Test d’auto-évaluation sur la partie B

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Objectif

Entraînement et évaluation partielle des vos compétences en modélisation.

Prérequis

Parties A et B

Question 1

On appelle séquenceur d’un mot binaire $a_1 a_2 … a_n$ le mot binaire $x_2 … x_n$ tel que $x_i = 1$ si et seulement si $a_{i-1} \neq a_i$.

Voici un exemple de mot binaire et de son séquenceur.

mot m :           001110000000
séquenceur de m :  01001000000

On considère les variables $A_1, …, A_n$ et $X_2, …, X_n$ ayant toutes pour domaines $\{0,1\}$.

Vous devez spécifier un réseau de contraintes $T_n$ tel que toute assignation $A_1=a_1,…,A_n=a_n$, $X_2=x_2,…,X_n=x_n$ satisfait $T_n$ si et seulement si le mot binaire $x_2 … x_n$ est le séquenceur du mot binaire $a_1 a_2 … a_n$.

Par exemple, l’assignation $A_1=1, A_2=0, A_3=1, X_2=1, X_3=1$ satisfait $T_3$ car 11 est le séquenceur de 101. Par contre l’assignation $A_1=1, A_2=0, A_3=1, X_2=0, X_3=1$ ne satisfait pas $T_3$ car 01 n’est pas le séquenceur de 101.

$T_n$ est constitué de $n-1$ contraintes nommées $q_1, …, q_{n-1}$.

Précisez les variables reliées par chaque contrainte. Donnez une spécification en extension et une spécification en compréhension (avec des opérations arithmétiques ou logiques) d’une de ces contraintes.

Réponse

Chaque contrainte $q_i$ relie les variables $A_i$, $A_{i+1}$ et $X_{i+1}$.

Exemple de spécification de $q_i$ en compréhension : $X_{i+1} = |A_{i}-A_{i+1}|$.

Spécification de $q_i$ en extension : sur $A_i$, $A_{i+1}$, $X_{i+1}$ : $\{(0,0,0),(1,1,0),(0,1,1),(1,0,1)\}$.

Question 2

En supposant que $n>3$, quelles contraintes faut-il ajouter au réseau $T_n$ de la question précédente pour exprimer que le mot binaire $a_1 a_2 … a_n$ comporte exactement une séquence de 3 bits à 1 consécutifs, tous les autres bits étant à 0 ?

On entend par là que si on note le réseau $T’_n$ le réseau obtenu en ajoutant à $T_n$ ces nouvelles contraintes, alors toute assignation partielle $A_1=a_1,…,A_n=a_n$ a une extension satisfaisant $T’_n$ si et seulement si le mot binaire $a_1 a_2 … a_n$ comporte exactement une séquence de 3 bits à 1 consécutifs, tous les autres bits étant à 0, comme dans les exemples suivants : 00111100, 000111, 111000000.

Les nouvelles contraintes sont à donner en compréhension.

Réponse

$\sum_{i=1}^n A_i = 3$ (Il y a trois bits à 1).
$\sum_{i=2}^n X_i \leq 2$ (Il y a au plus deux transitions).
$A_1 + A_n \leq 1$ (Il ne doit pas y avoir un bit à 1 aux deux extrémité)

Question 3

On considère un dirigeable dont la nacelle est scindée en trois parties : une cabine destinée aux passagers au milieu et deux compartiments de fret, nommés A et B, aux extrémités. Parmi $N$ objets, numérotés de 1 à $N$ et de poids $w_1, …, w_n$ , au moins $K$ doivent être embarqués en respectant les conditions suivantes :

La somme des poids des objets embarqués dans le compartiment A doit être égale à la somme des poids des objets embarqués dans le compartiment B.
La somme des poids des objets embarqués dans les deux compartiments ne doit pas dépasser une valeur W.

Les valeurs $K$ et W, ainsi que les poids des $N$ objets susceptibles d’être embarqués, sont des données connues. Vous devez modéliser ce problème sous la forme d’un réseau de contraintes utilisant exclusivement des variables à domaine {0,1}. Vous devez utiliser des contraintes arithmétiques linéaires construites à l’aide de sommes, produits d’une variable par une constante, opérateurs de comparaison ($=$, $\neq$, $<$, $>$, $\leq$, $\geq$). Précisez bien le rôle et la signification d’une assignation à 1 de chaque variable.

Réponse

Variables :

$A_1, … ,A_N$ de domaine $\{0,1\}$. $A_N=1$ signifie que l’objet numéro $i$ va dans le compartiment A.
$B_1, … ,B_N$ de domaine $\{0,1\}$. $B_N=1$ signifie que l’objet numéro $i$ va dans le compartiment B.

Contraintes :

$(\sum_{i=1}^n A_i) + (\sum_{i=1}^n B_i) \geq K$ (au moins $K$ objets embarqués)
$\sum_{i=1}^n w_i A_i = \sum_{i=1}^n w_i B_i$ (équilibre des charges)
$\sum_{i=1}^n w_i A_i + \sum_{i=1}^n w_i B_i \leq W$ (charge maximale autorisée)
Pour tout $i\in 1..N$, $A_i + B_i < 2$ (un objet est est embarqué dans un seul compartiment ou n’est pas embarqué)

Question 4

On considère 8 variables $X_1, X_2, Y_1, Y_2$, $X’_1, X’_2, Y’_1, Y’_2$ ayant toutes pour domaine l’ensemble $0..N$ des entiers naturels compris entre 0 et $N$.

Une assignation de ces variables représente deux rectangles situés dans un repère cartésien discret avec les conventions suivantes :

$X_1, Y_1$ sont les coordonnées du coin inférieur gauche du premier rectangle.
$X_2, Y_2$ sont les coordonnées du coin supérieur droit du premier rectangle.
$X’_1, Y’_1$ sont les coordonnées du coin inférieur gauche du deuxième rectangle.
$X’_2, Y’_2$ sont les coordonnées du coin supérieur droit du deuxième rectangle.

La figure ci-dessous représente un exemple de positions et formes des deux rectangles, mais il y a un très grand nombre d’autres possibilités.

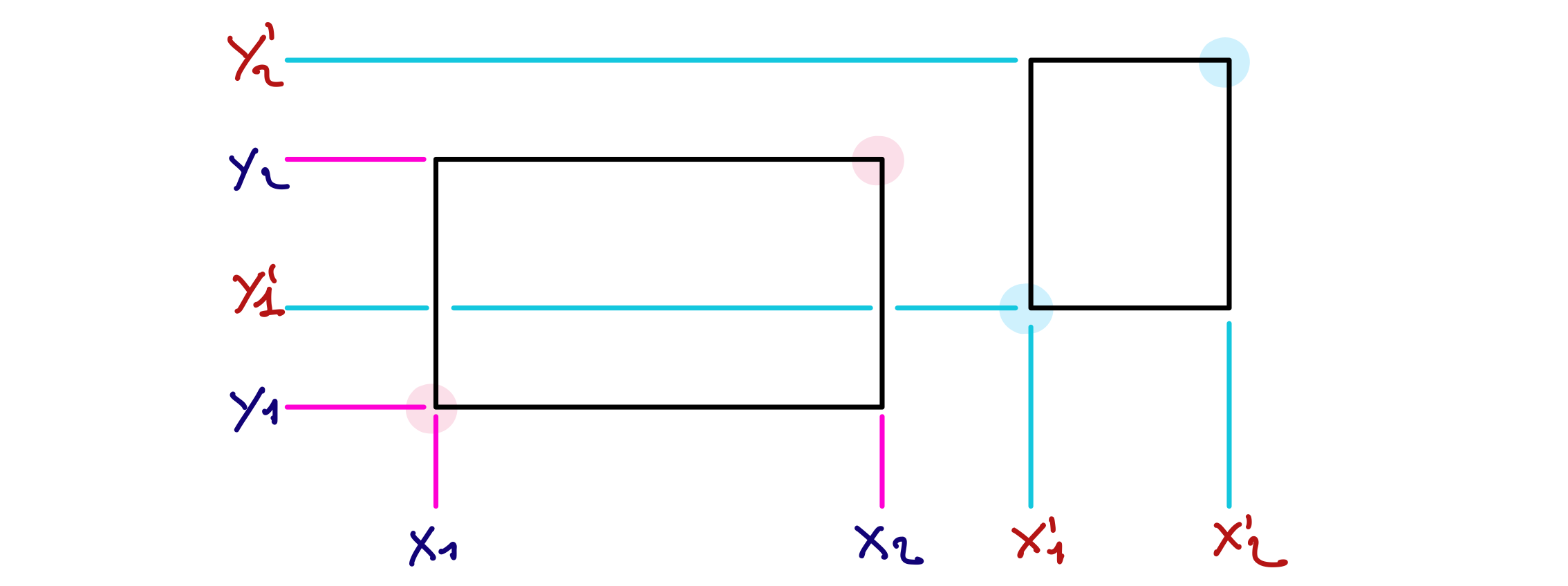
Vous devez spécifier les contraintes qui expriment que les deux rectangles se recouvrent (l’intersection entre les 2 est non vide). La ou les contraintes à écrire peuvent combiner des opérations arithmétiques (additions, soustractions, comparaisons) et logiques (et, non).

On suppose que $X_2 > X_1$, $Y_2 >Y_2$, $X’_2 > X’_1$ et $Y’_2 >Y’_2$.

Réponse

$X’_1 < X_2$,

$X_1 < X’_2$,

$Y’_1 < Y_2$,

$Y_1 < Y’_2$

Question 5

On considère un échiquier (une grille) de N par N. Une pièce appelée cavalier peut se déplacer sur cette grille en se décalant de deux positions horizontalement et d’une verticalement ou de deux positions verticalement et d’une horizontalement. La figure ci-dessous donne deux exemples indépendants dans lesquels la grosse pastille désigne la position initiale d’un cavalier et les petites pastilles désignent les cases pouvant être atteintes par ce cavalier.

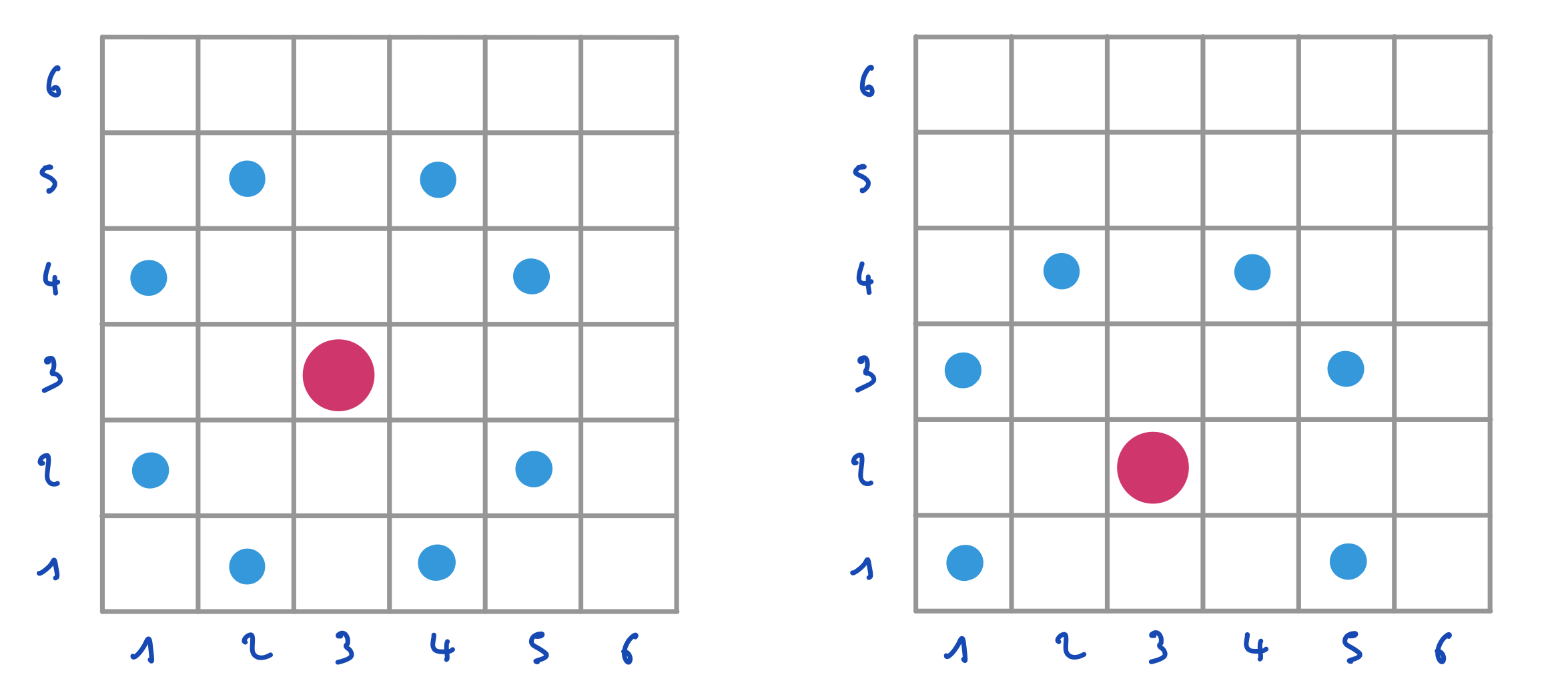
On considère les variables $X_1, Y_1, X_2, Y_2, V, H$ de domaines respectifs $1..N$, $1..N$, $1..N$, $1..N$, $\{-2,-1,1,2\}$, $\{-2,-1,1,2\}$.

Donnez en compréhension les contraintes qui spécifient qu’un cavalier situé en position $(X_1,Y_1)$ peut aller en $(X_2,Y_2)$ en se déplaçant de $H$ cases horizontalement et de $V$ case verticalement.

Réponse

$|X_1-X_2| = H$
$|Y_1-Y_2| = V$
$H\neq V$

Question 6

On numérote de la manière suivante les 8 déplacements réalisables par un cavalier sous réserve que les cases de destination soient dans les limites de l’échiquier.

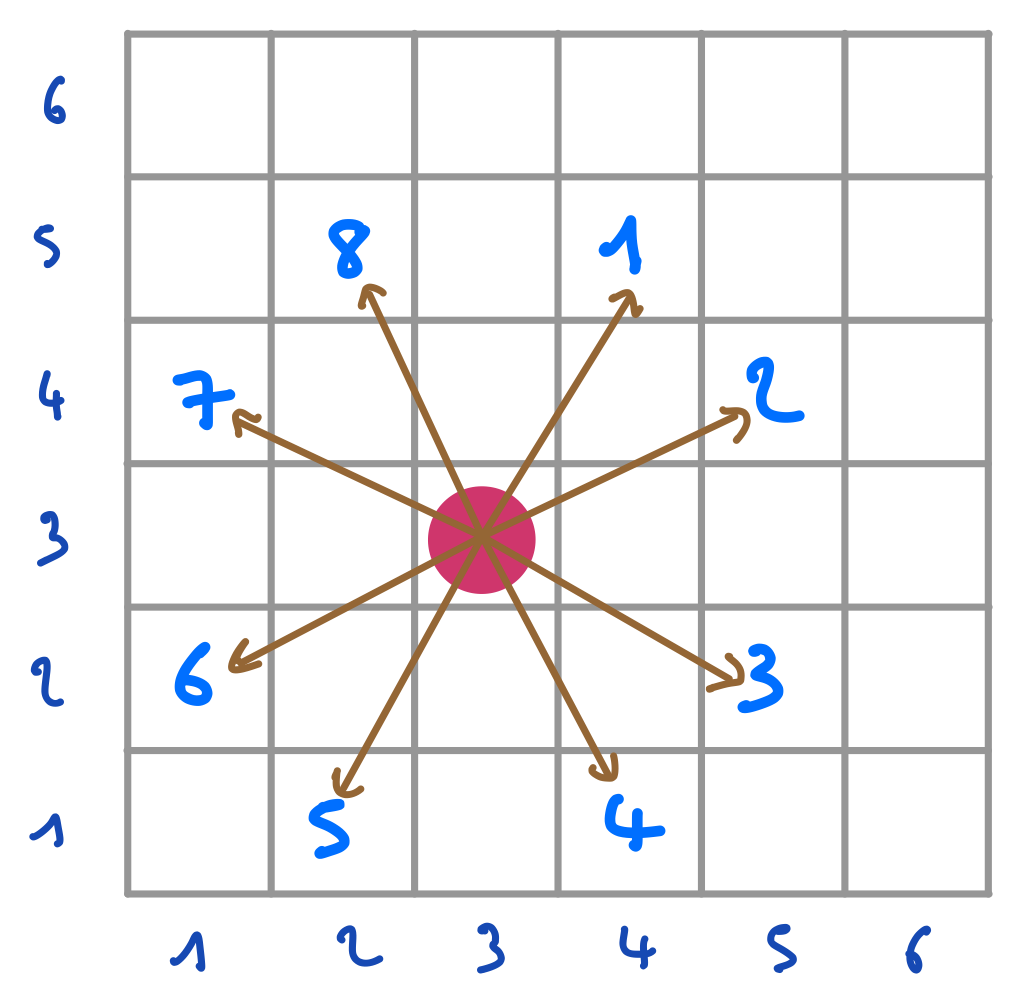
On ajoute une variable $D$ de domaine $1..8$ au réseau de contraintes précédent. Donnez en extension la contrainte à ajouter entre $V$, $H$ et $D$ pour que dans toute assignation satisfaisant toutes les contraintes, $D$ aie pour valeur le numéro du déplacement correspondant aux valeurs de $V$ et $H$.

Réponse

Sur $V,H,D$ : $\{(2,1,1),(1,2,2),(-1,2,3),(-2,1,4),(-2,-1,5),(-1,-2,6),(1,-2,7),(2,-1,8)\}$