PPC : test d’autoévaluation partie A

Programmation par contraintes

En M2 Bases de données et IA et M2 Image et IA

Par Olivier Bailleux, Maître de conférences HDR, Université de bourgogne

Test d’auto-évaluation sur la partie A

Objectif

Vérifier si vous avez assimilé de manière approfondie les notions de la partie A

Prérequis

Partie A

Question 1

Pour chacune de ces deux contraintes, dites si elle est donnée en extension et/ou en compréhension et/ou sous forme énumérative. On suppose que les variable ont toutes pour domaines ${1,2,3}$.

  1. $A > C+1$
  2. sur $A,B,C$, ${(1,1,1),(1,2,1),(2,1,2)}$
"Réponse"

La première contrainte est en compréhension. La deuxième est en extension. Elle est donnée sous forme énumérative. (Les deux termes sont équivalents.)

Question 2

Le réseau de contraintes suivant a-t-il des solutions ? Si oui, donnez les.

![](img

"Réponse"

Ce réseau n’a pas de solution. Il est incohérent.

Question 3

Le réseau de contraintes suivant a-t-il des solutions ? Si oui, donnez les.

"Réponse"

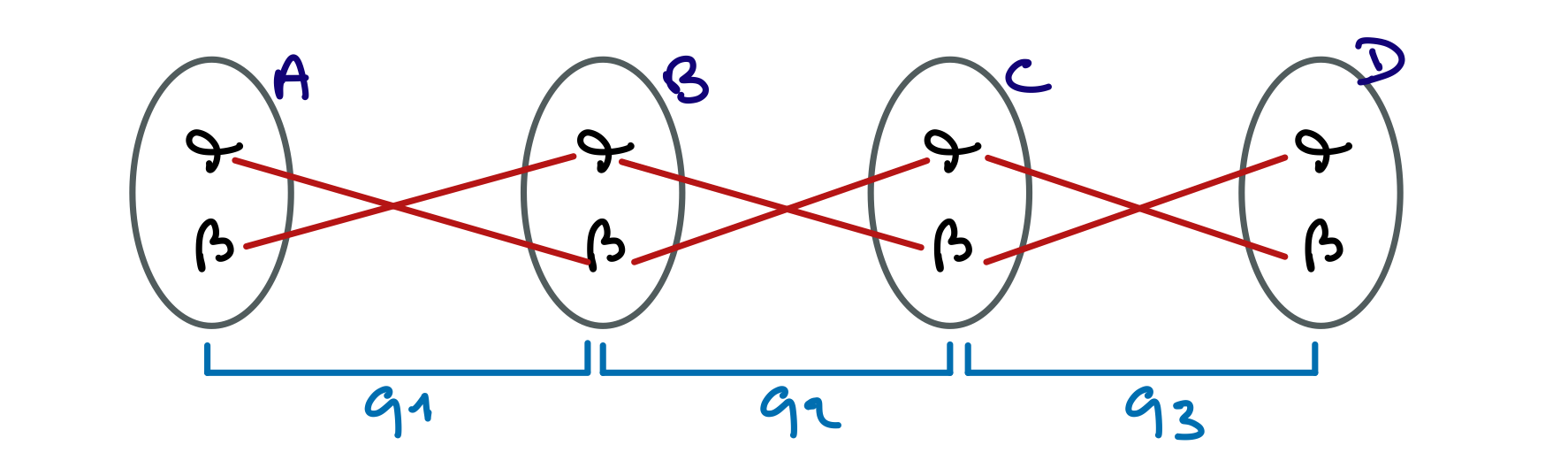
  1. $A=\alpha, B=\beta, C=\alpha, D=\beta$
  2. $A=\beta, B=\alpha, C=\beta, D=\alpha$

Question 4

On dit que deux contraintes sont équivalentes si et seulement si elles relient les mêmes variables, de même domaines, et sont satisfaites par les même assignations de ces variables.

Soit $A$ et $B$ deux variables à domaine ${0,1}$. Les contraintes $A=\neg B$ et $A\vee B$ sont elles équivalentes ?

"Réponse"

Non, car l’assignation $A=1,B=1$ falsifie la première contrainte et satisfait la deuxième.

Question 5

Soit $A$ et $B$ deux variables à domaine ${0,1}$. Les contraintes $A=\neg B$ et $(A\vee B)\wedge(\neg A\vee \neg B)$ sont elles équivalentes ?

"Réponse"

Oui.

Question 6

Soit la contrainte $10 A + 5 B + C \leq 11$, où $A$, $B$ et $C$ ont pour domaine ${0, 1}$.

Donnez une assignation partielle $I$ qui falsifie cette contrainte et une assignation partielle $J$ qui la satisfait.

"Réponse"

$I$ : $A=1, B=1$.

$J$ : $A=0$ ou $B=0$ ou toute extension de ces assignations.

Question 7

Soient $A$ et $B$ deux variables ayant pour domaine ${0,1}$. Donnez une contrainte équivalente à $A = \neg B$ spécifiée en compréhension en utilisant uniquement des opérateurs arithmétiques +, -, = et des constantes entières (0, 1, …).

"Réponse"

$A = 1 – B$ ou $B= 1 – A$ ou $A+B = 1$.

Question 8

Soient les variables $A$ et $B$ de domaine ${0,1}$ et les variables $X$ et $Y$ de domaine ${0,2}$.

On considère :

  • la contrainte $q : A\vee B$,
  • et le réseau $r : A\neq X, B\neq Y, X\neq Y$.

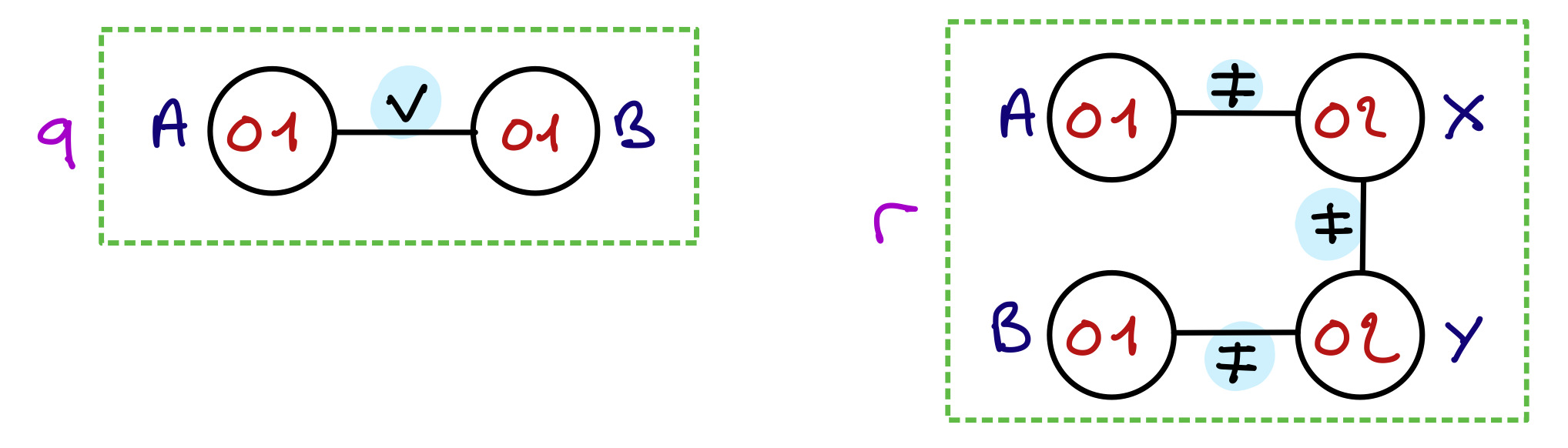
Soit $I$ une assignation des variable $A,B$, qui est aussi une assignation partielle des variables de $r$. Parmi les affirmations suivantes, lesquelles sont vraies ?

  1. Si $I$ satisfait $q$ alors il existe une extension de $I$ qui satisfait $r$.
  2. Si il existe une extension de $I$ qui satisfait $r$ alors $I$ satisfait $q$.
  3. Si $I$ falsifie $q$ alors $I$ (vu comme une assignation partielle des variables de $r$) falsifie $r$.
  4. Si $I$ satisfait $q$ alors $I$ (vu comme une assignation partielle des variables de $r$) satisfait $r$.
"Réponse"

  1. Oui. On peut vérifier que pour chacune des assignations qui satisfont $q$, c’est à dire ${A=0,B=1}$, ${A=1,B=0}$, et ${A=1, B=1}$, il existe une valeur de $X$ et une valeur de $Y$ qui permettent de satisfaire $r$.
  2. Oui. Il existe une extension de $I$ qui satisfait $r$ si $I={A=0,B=1}$ ou si $I={A=1,B=0}$ ou si $I={A=1, B=1}$. (et pas si $I={A=0, B=0}$). Ces trois assignations satisfont $q$.
  3. Oui. La seule assignation $I$ qui falsifie $q$ est ${A=0, B=0}$. Cette assignation falsifie $r$.
  4. Non. Par exemple, $A=1,B=1$ satisfait $q$ mais son extension $A=1,B=1,X=2,Y=2$ falsifie $r$.